基于变寿命模型的改善风电可调度性的电池储能容量优化

易 林 娄素华 吴耀武 杨天蒙

(强电磁工程与新技术国家重点实验室(华中科技大学) 武汉 430074)



基于变寿命模型的改善风电可调度性的电池储能容量优化

易 林 娄素华 吴耀武 杨天蒙

(强电磁工程与新技术国家重点实验室(华中科技大学) 武汉 430074)

基于风电接入技术准则和电网调度需求，对风电场日前调度功率值予以优化，并通过电池储能弥补实际风电出力与该调度参考值间的差值，从而改善风电的可调度性。从能量吞吐量角度出发，建立电池储能实际使用寿命评估模型。基于该模型，以风储联合系统年收益最大为目标，提出综合考虑风电调度功率优化和变寿命特性的电池储能容量优化模型。以某风电场年历史出力数据为例，对电池储能功率/电量容量进行协调优化，仿真结果验证了所提模型的有效性。

寿命预测模型 风电调度功率 电池储能系统 可调度性 容量优化配置

0 引言

随着化石能源危机及环境保护问题的日益突出，风能作为一种清洁可再生能源在电力工业中得到快速发展。然而，风能具有强烈的随机性、间歇性和难以预测性，这些特点导致风电场难以持续输出稳定的功率，其发电可调度性差，大规模风电并网将给电力系统的安全可靠运行带来不利影响[1，2]，从而对电网调度提出了新的要求与挑战。为了使可调度性差的风电适应确定性的电网调度决策，应对并网风电场的输出功率随机波动水平予以限制[3]。快速储能技术具有对功率和能量的时间迁移能力，能有效改善风电的输出特性，增强风电的可调度性，是解决风电大规模并网问题及促进风资源利用的关键技术[4-7]。

目前，国内外学者针对电池储能系统(Battery Energy Storage System，BESS)在风电场中的应用问题展开了研究，并取得了一定的研究成果。文献[8]提出了采用离散傅里叶变换对可再生能源出力进行频谱分析，并基于分析结果及平抑目标功率求取系统所需的最小储能容量。文献[9]基于风电场的风速概率分布及风电机组的出力特性，求取了以风电场平均出力为风储联合系统目标出力的储能容量需求。文献[10]为适应系统调度计划，以单个调度时段内等效输出方差和最小为目标求取了该时段风储联合系统的计划出力，并对储能系统容量进行了优化配置，但其未考虑相邻调度时段的风电功率波动约束，且未对电池储能功率/电量容量进行协调优化。

电池储能的使用寿命是容量优化的关键参量之一，其变寿命特征开始受到相关研究人员的关注[11-16]。文献[11]以铅酸蓄电池为例，综述了电池储能寿命预测方法。文献[12]利用超级电容吸收风电高频波动以减少电池储能充放电次数及放电深度，从而延长电池储能的使用寿命。文献[13]基于Peukert公式构建了电池储能寿命模型，并研究了用于微网的铅酸蓄电池能量管理策略以延长其使用寿命。文献[14]基于提出的寿命模型，针对3种不同应用场合对电池储能容量进行了优化配置。文献[15]从循环次数角度(cycle counting)构建BESS的寿命评估模型，并将其作为度量指标对控制策略进行了研究。文献[16]将文献[15]的寿命测算模型引入到电池储能的容量优化中，但未考虑日前风电调度功率值对储能系统运行状态以及使用寿命的影响。事实上，电池储能的使用寿命与其运行方式密切相关，而风电的调度功率直接关系到电池储能的运行方式。因此，有必要对考虑风电调度功率优化和变寿命特征的储能容量配置问题进行深入研究。

本文结合风电入网技术准则和调度运行计划特点，优化制定风电调度功率值，通过电池储能的引入使风储联合系统出力跟踪该功率值，从而使可调度性差的风电适应现行的电网调度决策。根据电池的运行特性，从能量吞吐量角度出发建立了BESS使用寿命计算模型。基于上述模型，以风储联合系统年收益最大为目标，提出了考虑风电调度功率优化和变寿命特征的BESS容量优化方法。利用本文所提方法对某实际风电场进行了电池储能容量的优化配置研究和结果分析。

1 风储联合系统及寿命预测模型

1.1 风电/电池储能联合发电系统

根据电池储能在风电场安装位置的不同，可分为集中式和分散式储能，集中式储能安装在风电场的并网点，能有效利用不同风机间的自平滑特性，便于对风电场的出力进行集中控制和调节，是目前广泛采用的方式。图1为典型的含集中式电池储能的风力发电系统并网结构示意图。

图1 含集中式电池储能的风力发电系统Fig.1 Schematic diagram of the wind farm -BESS interconnected to grid

图1中，Pb为电池储能系统的充/放电功率；PW为风电场的出力；PZ为风-储联合系统的总出力。

PZ=PW+Pb

(1)

通过储能的充放电出力弥补实际风电与调度功率之间的差值，使风储联合系统并网功率PZ的变化满足调度部门对接入风电场发电出力的技术要求，提高风电的可调性。

1.2 电池储能经济使用寿命预测模型

电池储能的使用寿命受温度、放电功率、充放电状态转换及放电深度(Depth of Discharge，DOD)等因素的影响[17-19]。放电深度为本文研究内容涉及的主要因素，为了简化问题、突出关键点，本文仅考虑该因素的影响。

电池储能的循环使用次数有限，且与其实际运行过程中的放电深度密切相关。运行过程中放电深度越大，循环使用次数越少，反之越多。基于实验数据，拟合电池储能使用次数与放电深度间的函数关系为

(2)

式中：Dr、Da分别为额定放电深度与实际放电深度；Nr、Na分别为对应于额定/实际放电深度的循环使用次数；α1、α2为函数关系式的拟合系数。

研究表明，电池储能对应于额定放电深度下的有效放电电量是一定的[18，19]。额定放电深度下，BESS使用寿命内其放电电量计算公式为

Er=NrDrEB

(3)

式中：Er为额定放电深度下电池储能在其使用寿命内的放电电量，MWh；EB为电池储能的电量容量。

电池储能在与风电配合运行过程中会经历一系列不规则的充放电过程，不同放电过程具有不同的放电深度。某一放电过程中，其实际放电电量可等效为多少额定放电深度下的有效放电电量，取决于该放电过程的放电深度。

基于式(2)，设折算系数KDOD为

(4)

则在规划水平年内，一系列不同放电深度放电过程折算至额定放电深度下的有效放电电量为

(5)

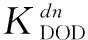
因此，电池储能的使用寿命Yb为

(6)

式中Yb为电池储能的使用寿命，a。

2 电池储能容量优化模型及运行策略分析

2.1 电池储能容量优化模型

1)目标函数

本文从风电商的角度出发，在满足电力调度上网要求的前提下，以风储联合系统的收益最大为目标，对风电场侧的电池储能容量进行优化配置。模型的目标函数不仅包含风储联合系统售电收益、电池储能投资等年值、年运行成本，还包含风储联合系统实际出力与其调度参考值之差而导致的惩罚费用，其数学表达式为

(7)

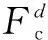
在实际运行中，受电池储能安装容量的限制，储能的功率输出可能无法完全弥补风电实际出力与调度参考值间的差异。当风储联合系统出力高于调度参考值时，将引起风电场强迫弃风，降低风电场的上网电量，减少风电场的收益；当风储联合系统出力低于调度参考值，将增大系统功率补偿成本甚至失负荷，使风电场将支付一定的罚金。某典型日d天内的惩罚费用为

(8)

式中

(9)

(10)

式中：Fcp(t)和Fcl(t)分别为该典型日内第t时段的弃风和缺电惩罚费用；kcp和kcl分别为单位弃风和缺电惩罚费用；PW，r(t)为对应时段的风电调度功率参考值。

电池储能的投资等年值和年运行费用为

FB=(kpPB+keEB)CRF(r,Yb)

(11)

(12)

Fk=kkPB+kvEB

(13)

式中：kp、ke分别为BESS单位功率和单位电量容量成本；kk、kv分别为BESS的单位功率和单位电量容量年运行维护费用；r为贴现率；Yb为式(6)所求的电池储能使用寿命；CRF(r,Yb)为等年值系数。

2)约束条件

考虑风电场和电池储能的运行特性，应满足如下运行约束条件。

①风电场运行约束

0≤PW(t)≤PW,R

(14)

式中：PW(t)为风电场在t时刻的出力；PW，R为风电场的额定装机容量。.

②电池储能运行约束

(15)

Ebmin≤Eb(t)≤EB

(16)

(17)

μ1∈{0,1},μ2∈{0,1},μ1+μ2≤1

(18)

式中：Eb(t)为电池储能在t时刻所存储的电量值；E0为初始存储电量值；Ebmin为电池储能存储电量的下限值；PB为电池储能的功率容量；ηc、ηd分别为充放电效率；μ1、μ2分别为BESS充放电状态变量：充电时，μ1=1，μ2=0；放电时，μ1=0，μ2=1。

2.2 电池储能运行策略分析

风电调度功率值影响电池储能的运行状态，从而间接影响电池储能的使用寿命，是其容量配置的重要因素之一。因此，本文结合前述寿命模型对风电调度功率值予以优化，即在满足风电接入技术要求的前提下，计及电网实际调度运行计划的需求，以调度期内电池储能综合出力最小为目标优化日前风电调度功率值，从而延长电池储能的使用寿命，如式(19)、式(20)所示。

(19)

(20)

式中：Pb，r(t)为电池储能在t时刻的出力参考值；γ为相邻调度时段的最大出力波动率。

基于制定的调度功率曲线及风电实际出力即可确定BESS在每个调度时段的充放电状态及出力值。然而，在实际运行中，对于确定规模的电池储能装置，计及其容量约束后，应对充放电功率予以调整，其调整后的BESS出力值Pb为

(21)

通过式(21)，可求得电池储能在各时刻的充放电状态及出力大小。由该式可知，电池储能的出力受其配置规模的影响较大，从而影响对风电可调度性的改善程度。

3 算例分析

本文以某一30 MW装机容量的风电场为例，应用本文所提模型对其配置的电池储能进行容量优化。风电上网电价k取0.1 $/kWh，单位弃风和缺电惩罚费用kcp和kcl分别取为0.1 $/kWh和1 $/kWh[20]。电池储能系统选择铅蓄电池，充放电效率均为90%，即综合转换效率为81%，其余相关参数如表1所示[16，21]。电池储能初始存储能量E0设为0.5EB[13]，使其具有充分的上调和下调容量空间；存储电量的下限值Ebmin为0.1EB；相邻调度时段允许最大出力波动率γ取12%，调度周期T取24 h，采样周期Δt为10 min，贴现率r取10%。

表1 电池储能参数Tab.1 Cell parameters for energy storape

本文对电池储能容量优化采用多场景分析和CPLEX优化引擎相结合的方法。采用CPLEX优化制定风电调度功率值，基于该调度功率曲线采用多场景分析法优化电池储能的容量配置规模。

3.1 电池储能配置规模对其使用寿命的影响

基于本文寿命模型及电池储能运行策略，以3 MW的功率容量为例，分析电池储能电量容量配置规模对其使用寿命的影响，如图2所示。

图2 BESS使用寿命随电量容量变化趋势(PB=3 MW)Fig.2 The lifetime of BESS with different energy capacities (PB=3 MW)

由图2可知，在相同的风电出力场景、运行策略及运行环境下，当电池储能的功率容量一定时，其使用寿命随电量容量配置规模的增大而延长。由BESS寿命预测模型可知，功率容量一定时，电量容量增大会使实际运行过程中放电深度减小，即同等放电电量下使BESS的损耗减小，从而使用寿命延长。因此，受电池储能运行特性的影响，其使用寿命并非固定不变，而是与其配置规模密切相关。在对BESS容量进行优化配置时，应充分考虑配置规模与使用寿命之间的关系。

3.2 电池储能配置规模对风电可调度性的影响

电池储能的功率和电量容量约束着其出力大小，也将对风电可调度性的改善效果产生影响。为了评估功率和电量容量对风电可调度性的影响，以两种典型的BESS配置规模为例分析其对应的风储联合系统出力，如图3所示。

图3 不同配置规模下的风储联合系统出力Fig.3 The output power of combined system with different BESS sizes

由图3可知，配置一定规模的电池储能可有效平抑风电功率波动，其改善效果与电池储能功率/电量容量的配置规模密切相关。当BESS功率容量较小时，其调度时段瞬时充放电出力有限，即使其电量容量足够大，仍无法弥补风电实际出力与其调度参考功率间的差值，如图3中配置规模为1 MW/4 MWh时风储联合系统在第5～20个采样周期的出力所示。当BESS电量容量较小时，受充放电累积效应的影响，若某调度时段电池储能已充电至额定电量容量或已放电至存储能量下限值，即使功率容量满足瞬时出力的要求，电池仍将停止充/放电，将会有部分调度功率参考值不能得到满足，如图3中电池容量为4 MW/1 MWh时风储联合系统在第80～100个采样周期内的出力曲线所示。

上述情况均使风电可调度性降低，从而引起不同程度的弃风或缺电现象。随着电池储能配置规模的增加，风电可调度能力逐步增强，当其配置容量达到一定规模时可使风电完全跟踪其调度计划值，但在实际工程应用中，应充分权衡风电可调度性的提高(技术性)与储能投资经济性之间的相互关系，从而对其容量需求进行优化配置。

3.3 电池储能容量优化配置分析

BESS容量优化配置包含功率容量和电量容量两部分。基于本文模型，以PB=3 MW为例，分析配置不同规模电量容量的BESS对系统各经济指标的影响，如图4所示。其中，风储联合系统年售电收益和年总收益对应左侧坐标轴，其余经济指标对应右侧坐标轴。

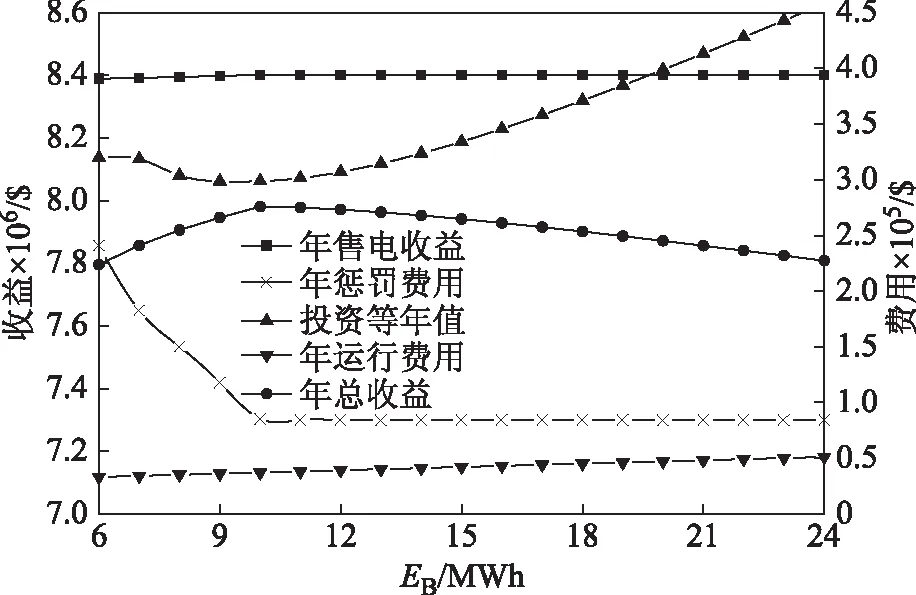
图4 不同BESS电量容量经济性分析(PB=3 MW)Fig.4 The total annual revenue with different energy capacities of BESS (PB =3 MW)

由图4可知，对于确定的功率容量，电池储能的投资等年值随其电量容量的增加呈先减小后上升趋势，而不是单调递增。这是由于当PB一定时，在EB增加初期，BESS的使用寿命随EB的增加明显延长(如图2所示)，因此其投资等年值反而呈下降趋势。随着EB的继续增加，虽然BESS的使用寿命仍有延长，但此时由于BESS的配置规模较大，投资总成本较大，因此其投资等年值转向上升趋势。当功率容量一定时，风储联合系统的年总收益随EB的增加先增加后减少。当电量容量较小时，电池储能无法满足跟踪风电调度功率参考值的要求，惩罚费用较大，其收益较小。随着EB的增加，BESS调节能力增强，风电实际出力与调度功率参考值间差值减少，惩罚费用减少，系统总收益增加。当电量容量配置到一定规模时，受储能功率容量的约束，惩罚费用趋于饱和，此时继续增加BESS电量容量的配置规模，由于储能投资等年值及运行维护成本的增加，系统年总收益转向下降趋势。

图5为不同功率/电量容量配置下的运行模拟结果，由图可知，不同功率容量下的最优电量容量均与PB=3 MW时呈类似变化趋势。此外，不同PB下的年最大总收益随PB的增加先增加后减少，其原因与EB对系统收益影响的分析类似。该风电场的BESS最优配置规模为3.7 MW/11 MWh，占风电场装机容量的12.3%，风储联合系统年最大总收益为801.8万美元，其中年售电收益为840.1万美元，惩罚费用为0.9万美元。可见，为实现系统经济效益的最大化，允许风储联合出力与调度功率参考值之间存在一定程度的差值，可在风电可调度性的改善与风储联合系统的经济性之间取得最佳平衡。

图5 配置不同规模BESS的系统年总收益Fig.5 The total annual revenue with different BESS sizes

3.4 两种寿命模型的对比分析

表2为固定寿命模型时不同寿命参数下的最优配置计算结果与可变寿命模型的对比分析。

表2 固定寿命模型与变寿命模型的比较Tab.2 Comparison between two lifetime models

由表2可知，固定寿命模型中，Yb取值不同时，其最优配置规模下的年总收益相差较大。当BESS寿命参数取值过小时，受较高投资等年值的影响，电池储能的最优功率/电量容量均较小。较小的配置规模将在很大程度上无法满足跟踪风电调度功率的要求，惩罚费用较高，从而导致风储联合系统的总收益较低。由于风电场对用于改善风电可调度性的储能容量需求较小(约占风场装机容量的10%左右)，因此储能的总投资成本相对较小。随着BESS寿命参数取值的增加，不同配置规模下的投资等年值差距缩小，此时电池储能的最优配置规模主要受跟踪风电调度功率需求的影响(体现为惩罚费用)。因此较高寿命参数下的电池储能最优配置规模整体提升，均为3.7 MW/10 MWh，该配置规模下的惩罚费用趋于饱和，能在存在一定惩罚的情况下实现经济收益最佳。

由于电池储能的最优功率容量主要取决于瞬时充放电需求，因此当固定寿命模型寿命参数取值较大时，两种寿命模型下的最优功率容量相同。然而，由于变寿命模型综合考虑了实际运行过程放电深度对电池使用寿命的影响，因此在相同功率容量配置下，变寿命模型的最优电量容量比固定寿命模型配置规模高10%，为11 MWh。

由上述分析可知，使用寿命是影响电池储能容量需求评估的关键参量之一。在电池储能规划阶段，考虑其变寿命特征十分必要。固定寿命模型因未考虑实际运行过程对使用寿命的影响，不同寿命取值会对电池储能的经济效益和容量需求评估产生偏差。相较于固定寿命模型，可变寿命模型能更合理地评估电池储能的经济效益及容量需求。

4 结论

电池储能技术的迅速发展为其在含风电电力系统中的规模化应用提供了新的契机。本文立足于电网对风电接入的技术要求，通过电池储能灵活的充放电特性改善风电的可调度能力，结合放电深度对电池储能使用寿命的影响，建立了电池储能使用寿命预测模型，并将其引入到风储联合系统的电池储能容量需求评估中。算例表明，通过合理配置电池储能容量，能有效提高风电的可调度能力，且相较于固定寿命模型，本文所提模型能更客观、准确地评估风电场对电池储能的容量需求及其经济效益。

[1] 邓卫，唐西胜，裴玮，等.含风电微型电网电压稳定性分析及控制技术[J].电工技术学报，2012，27(1)：56-62. Deng Wei，Tang Xisheng，Pei Wei，et al.Voltage stability and control technologies of Micro-Grid with wind power[J].Transactions of China Electrotechnical Society，2012，27(1)：56-62.

[2] 何世恩，董新洲.大规模风电机组脱网原因分析及对策[J].电力系统保护与控制，2012，40(1)：131-137，144. He Shien，Dong Xinzhou.Cause analysis on large-scale wind turbine tripping and its countermeasures[J].Power System Protection and Control，2012，40(1)：131-137，144.

[3] GB/T 19963—2011，风电场接入电力系统技术规定[S].北京：中国标准出版社，2011.

[4] 娄素华，吴耀武，崔艳昭，等.电池储能平抑短期风电功率波动运行策略[J].电力系统自动化，2014，38(2)：17-22，58. Lou Suhua，Wu Yaowu，Cui Yanzhao，et al.Operation strategy of battery energy storage system for smoothing short-term wind power fluctuation[J].Automation of Electric Power Systems，2014，38(2)：17-22，58.

[5] 姚勇，朱桂萍，刘秀成.电池储能系统在改善微电网电能质量中的应用[J].电工技术学报，2012，27(1)：85-89. Yao Yong，Zhu Guiping，Liu Xiucheng.Improvement of power quality of Micro-Grids by battery energy storage system[J].Transactions of China Electrotechnical Society，2012，27(1)：85-89.

[6] Jiang Quanyuan，Wang Haijiao.Two-time-scale coordination control for a battery energy storage system to mitigate wind power fluctuations[J].IEEE Transactions on Energy Conversion，2013，28(1)：52-61.

[7] 张坤，毛承雄，陆继明，等.基于储能的直驱风力发电系统的功率控制[J].电工技术学报，2011，26(7)：1-8. Zhang Kun，Mao Chengxiong，Lu Jiming，et al.Power control strategy of directly drive wind turbine with energy storage system[J].Transactions of China Electrotechnical Society，2011，26(7)：1-8.

[8] 王成山，于波，肖俊，等.平滑可再生能源发电系统输出波动的储能系统容量优化方法[J].中国电机工程学报，2012，32(16)：1-8. Wang Chengshan，Yu Bo，Xiao Jun，et al.Sizing of energy storage systems for output smoothing of renewable energy systems[J].Proceedings of the CSEE，2012，32(16)：1-8.

[9] 韩涛，卢继平，乔梁，等.大型并网风电场储能容量优化方案[J].电网技术，2010，34(1)：169-173. Han Tao，Lu Jiping，Qiao Liang，et al.Optimized scheme of energy-storage capacity for grid-connected large-scale wind farm[J].Power System Technology，2010，34(1)：169-173.

[10]冯江霞，梁军，张峰，等.考虑调度计划和运行经济性的风电场储能容量优化计算[J].电力系统自动化，2013，37(1)：90-95. Feng Jiangxia，Liang Jun，Zhang Feng，et al.An optimization calculation method of wind farm energy storage capacity[J].Automation of Electric Power Systems，2013，37(1)：90-95.

[11]Sauer D U，Wenzl H.Comparison of different approaches for lifetime prediction of electrochemical systems——using lead-acid batteries as example[J].Journal of Power Sources，2008，176(2)：534-546.

[12]Gee A M，Robinson F V P，Dunn R W.Analysis of battery lifetime extension in a small-scale wind-energy system using supercapacitors[J].IEEE Transactions on Energy Conversion，2013，28(1)：24-33.

[13]Tran D，Khambadkone A M.Energy management for lifetime extension of energy storage system in micro-grid applications[J].IEEE Transactions on Smart Grid，2013，4(3)：1289-1296.

[14]Jenkins D P，Fletcher J，Kane D.Lifetime prediction and sizing of lead-acid batteries for microgeneration storage applications[J].IET Renewable Power Generation，2008，2(3)：191-200.

[15]严干贵，朱星旭，李军徽，等.内蕴运行寿命测算的混合储能系统控制策略设计[J].电力系统自动化，2013，37(1)：110-114. Yan Gangui，Zhu Xingxu，Li Junhui，et al.Control strategy design for hybrid energy storage system with intrinsic operation life measurement and calculation[J].Automation of Electric Power Systems，2013，37(1)：110-114.

[16]韩晓娟，程成，籍天明，等.计及电池使用寿命的混合储能系统容量优化模型[J].中国电机工程学报，2013，33(34)：91-97. Han Xiaojuan，Cheng Cheng，Ji Tianming，et al.Capacity optimal modeling of hybrid energy storage systems considering battery life[J].Proceedings of the CSEE，2013，33(34)：91-97.

[17]Bindner H，Cronin T，Lundsager P，et al.Lifetime modelling of lead acid batteries[R].Roskilde：Risø National Laboratory，2005.

[18]Drouilhet S，Johnson B.A battery life prediction method for hybrid power applications[R].Golden：U.S.Department of Energy，1997.

[19]Babazadeh H，Gao W，Duncan K.A new control scheme in a battery energy storage system for wind turbine generators[C].IEEE Power and Energy Society General Meeting，San Diego，CA，2012：1-7.

[20]Bouffard F，Galiana F D.Stochastic security for operations planning with significant wind power generation[J].IEEE Transactions on Power System，2008，23(2)：306-316.

[21]Chacra F A，Bastard P，Fleury G，et al.Impact of energy storage costs on economical performance in a distribution substation[J].IEEE Transactions on Power System，2005，20(2)：684-691.

Optimal Battery Capacity Based on Lifetime Predicationfor Improving the Schedulability of the Wind Power

YiLinLouSuhuaWuYaowuYangTianmeng

(State Key Laboratory of Advanced Electromagnetic Engineering and Technology Huazhong University of Science and Technology Wuhan 430074 China)

Based on the technical rule for connecting the wind farm to the power system and the requirements of the power system dispatching，the wind farmday-ahead dispatching power is optimized.The battery energy storage system (BESS) is used to meet the difference between the wind power and the referencevalue to improve the output characteristics and the schedulability of the wind power.From the energy throughput standpoint，a battery lifetime prediction model is developed and introduced into the optimization model.The optimal capacity of the installed BESS is determined，with which the wind power and the storage system can achieve maximum revenue and the power optimization and lifetime characteristics are both considered.Comparing to thetraditional approaches without lifetime predication，the calculation results with real wind farm historical output power demonstratethe feasibility and the effectiveness of this model.

Lifetime model，wind power dispatchingvalue，battery storage system，schedulability，capacity optimization

国家自然科学基金(51207062)和国家重点基础研究发展(973)计划(2012CB215102)资助。

2014-12-10 改稿日期2015-03-14

TM732

易 林 男，1990年生，硕士研究生，研究方向为电力系统规划与优化运行、新能源发电、储能系统优化。

娄素华 女，1974年生，博士、副教授，研究方向为电力系统规划与优化运行、新能源发电和电力技术经济。(通信作者)