Merton违约距离模型对企业财务困境的预测能力研究
——基于离散时间风险模型的实证分析
蔡玉兰, 崔 毅
(华南理工大学 工商管理学院,广东 广州 510641)
Merton违约距离模型对企业财务困境的预测能力研究
——基于离散时间风险模型的实证分析
蔡玉兰, 崔 毅
(华南理工大学 工商管理学院,广东 广州 510641)
本文基于违约距离函数形式的考虑,将违约距离分别视作由3个变量、3个决定要素和2个拆分项组成的综合指标,采用离散时间风险模型技术,通过信息量检验和十分位预测实证分析了Merton违约距离模型对企业财务困境的预测能力。结果发现,Merton违约距离模型所给出的违约距离的非线性函数形式相对于其构成指标而言并不是最重要的,违约距离过于概括和抽象反而遗漏了一些重要信息,以致其预测能力还不及其3组构成指标简单的线性组合。实际上,违约距离的显著预测能力来自于其度量了资产波动性对企业发生财务困境的直接和间接影响。
Merton违约距离模型;财务困境;预测能力
1 引言
目前,Merton违约距离模型(Merton Distance-to-Default Model, Merton DD模型)已成为企业财务困境预测研究的主流方法之一[1]。国内已涌现出大量基于Merton DD模型的财务困境预测研究成果,但这些研究主要集中在模型的适用性验证和方法改进上[2]。大多数研究指出Merton DD模型在财务困境预测中有较好的表现,但都是基于违约距离(DD)对两类公司的判别能力所给出的结果,还没有学者从DD本身入手,研究其函数形式、构成要素与其预测能力的关系。换句话说,大多数学者都在使用Merton DD模型,却对模型本身的属性认识不足。我们之所以有此疑问,是因为Merton违约距离模型同Altman[3]的Z-score模型都是信用违约史上里程碑式的成果,但两者并不具有同等的预测效力[4,5]。二者除了信息来源不同以外,最大的差异就在函数形式上。Z-score模型是几个财务比率简单的线性组合,而DD则是多个变量的非线性函数,比Z-score模型要复杂得多。国外学者Bharath和Shumway[6]指出,Merton DD模型的重要性就在于它所给出的DD的函数形式。然而他们的论证却是不充分的。他们只将决定模型最终输出结果的4个变量(E、F、μ、σE)同违约概率(Pdef)一起纳入Cox模型中进行实证检验,发现在包含了这些变量的情况下,Pdef仍与违约风险的发生显著正相关,而且其参数值(绝对值)比这些变量要大得多,从而得出Merton DD模型的价值就在于DD的函数形式的结论。
虽然从Merton DD模型基本原理出发,DD是由这几个变量所构成,但Crosbie和Bohn[7]在详细介绍Merton DD模型应用的技术框架时指出,一个公司发生违约的可能性主要取决于以下3个因素:资产市场价值(V),资产的风险(σV)以及杠杆率(F/V),DD就是由这3个因素综合而成的单一指标。Bharath和Shumway并没有将这3个因素连同Pdef一起进行模型估计,而且我们还推断,他们并没有对模型估计的标准误加以调整,从而进入模型的所有变量都在1%的水平上显著。另外,从另一个视角出发:将DD拆分成类似于Z-score模型的线性形式(将如下所示,这种拆分也是很有意义的),对拆分后的单项因子进行模型估计又会得到怎样的结果?Bharath和Shumway也没有考虑。
鉴于此,本文将同时考虑Bharath和Shumway未曾考察的两个方面,并按照他们的研究设计进行实证分析,以对Merton DD模型有更进一步的认识。所不同的是,我们将采用离散时间风险模型进行模型估计,如下所示,这种建模技术具有一系列其他模型无法比拟的优势。
2 离散时间风险模型
离散时间风险模型(Discrete Time Hazard Model,DTHM)起源于生存分析(Survival Analysis),是一种包含了时间序列数据的技术方法,特别适用于分析那些由二元的、时间序列和截面观测值所组成的数据,如破产数据[4]。DTHM与logit模型紧密相关,其函数形式如下
(1)
其中α(t)为时变的基准风险率(Baseline Hazard Rate),X是解释变量集,β是参数向量,下标i和t表达了对每一个公司i使用多个年度观测值。相比一般的logit模型,DTHM具有以下优势:第一,DTHM引入了时间变量,考虑了事件发生概率随时间变化的情况,这与实际更加相符。由于考虑了时间因素,DTHM能够模拟企业陷入财务困境的动态过程,这意味着从理论上DTHM有更高的预测准确度[8]。第二,DTHM比较适合处理删失数据(Censoring Data)。由于建模样本通常是选取某一时间段作为样本观测期,DTHM中观测期内未发生财务困境的企业被当作删失对象(删失意味着他们发生财务困境的具体时间是未知的),这种假定更准确地模拟了现实情况[9]。而一般的logit模型将删失数据当作截面数据处理,从而导致较大的偏差[10]。第三,DTHM使用了所有可用的公司-年观测数,能带来更有效的参数估计。普通的logit模型因常采用配对抽样的研究设计而限制了样本观测数据量,但DTHM使用了每一个公司生存时间内的所有数据,大大提高了样本量,使得估计的结果更加准确。
在DTHM中,风险率(Hazard Rate)是企业在生存至时间t的条件下在下一刻陷入财务困境的概率。如果企业在时间t陷入财务困境,因变量y取值为1,反之则为0。生存时间界定为公司自上市以来直至发生财务困境的时间,并以年为单位。Shumway[11]指出,由于DTHM可视为一个多周期logit模型,故可通过logit模型的估计程序来估计DTHM。此时,每年生存着的公司(删失样本集)都被视为财务正常样本,其y值皆为0,而每一个财务困境公司对logit程序只贡献一个y=1的观测值,即被ST当年y取值为1,其他年份则为0。
由于DTHM使用的是公司-年观测数据,模型估计所产生的检验统计量(标准误及卡方值)是不正确的,因为它假定用于估计模型的独立观测值的数量是公司-年的数目。但实际上一个特定公司的公司-年观测值并不是独立的,因为如果该公司在t-1时刻陷入财务困境,其最后一期观测值绝不可能为t时刻;而一个公司能生存至t时刻,绝不可能在t-1时刻被划为财务困境公司。在DTHM中,每个公司的整个生命跨度(Entire Life Span)才是一个独立的观测值[12],因而需要对模型参数估计的标准误或卡方值加以调整。Petersen[12]和Thompson[13]详细讨论了这类数据独立性缺乏的问题,并指出可通过对参数估计的标准误加以Cluster聚类调整来解决。SAS 9.2软件中有专门的Cluster语句程序来实现这一过程。
3 Merton DD模型
有关Merton DD模型的最终输出结果可见Crosbie和Bohn的详细推导,这里直接给出结果
(2)
Pdef=N(-DD)
(3)
其中V为公司资产价值;F为公司负债的账面价值;μ为预期资产收益率;σV为公司资产价值的波动性;T为债务到期时间。
不过,本文只采用DD作为核心指标。这是因为,严格来讲,Pdef并不是一个财务困境概率,真实的财务困境概率是基于经验分布获得的,而Pdef却是在假定的正态分布下获得的。采用DD不仅可以避免这种分布上的不一致问题,也可以将其视作同Z积分值一样的表达。
(2)式中V和σV是不可直接观测的。对于二者的计算,详见Cui和Cai[14],在此不加详述。
由于截止目前DD的拆分项究竟表达了什么,还鲜有研究涉及到,故而在此略加论述。根据(2)式,在设定T=1的条件下,DD可拆分为
(4)
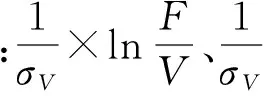

(5)
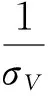
在财务管理上,公司资产价值的波动性实际上体现了企业的经营风险状况,而杠杆率反映企业的财务风险,于是DD对企业财务困境的作用便可描述为如下所示的理论关系:
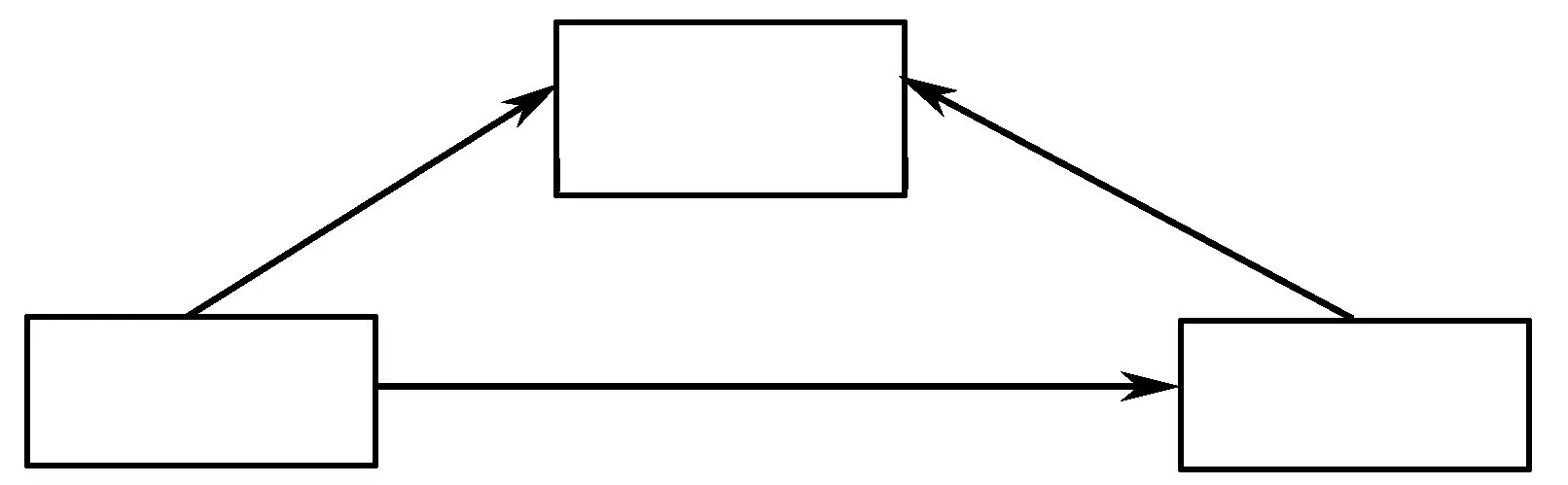
图1 DD拆分后的理论解释
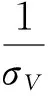
4 样本及数据
按照国内学者研究的惯例,本文界定“因财务状况异常”而被特别处理(ST)为财务困境的标志。由于ST政策于1998年才开始实施,本研究即以1998年作为ST观测的起始时间。根据证监会对上市公司进行特别处理条款的规定,如果一家上市公司连续两年亏损或每股净资产低于股票面值,就要予以特别处理。故而,1998年被ST的公司,最晚也是1996年上市的。而很有可能,在1996年之前上市的公司,在1998年之前的某2年内,已经符合ST的条件,只因ST政策未予以实施而不属于ST公司。这些公司都属于左删失的情况,即在ST观测期之前已经发生财务困境但数据并未被记录,本研究不予以考虑。因而,本文的样本对象界定为1996年及以后上市的公司,观测这些公司在1998年至2014年因财务状况异常而被ST的状况。同已有的研究相一致,本文只检验上市公司首次发生ST的可能性,并剔除了金融类企业和连续观测数不足3年的公司。由此,样本公司皆为1996年至2011年上市的非金融企业,最终发生财务困境的上市公司共有334家,相比国内已有的研究,样本量已足够大且相对完整。财务正常公司由满足上述条件的非ST公司所组成,共有1378家。
根据离散时间风险模型对观测数据的要求,每个公司在其生存期间的每一年都有一个观测值,样本公司数是以公司-年来度量的。因而,对于ST公司,其最后一期观测值为ST前1年(因财务报告披露的滞后性),而对于非ST公司,其最后一期观测值为2013年。经统计各年间的样本公司数及公司-年观测数,最终得到16000个样本公司-年观测数,其中ST公司有2657个公司-年观测数,占比2.09%。
5 实证结果
5.1 信息量检验
信息量检验(Relative Information Content Test)检测一个变量(或一组变量)是否比另一个变量(或一组变量)提供了更多的信息[4]。基于离散时间风险模型估计所给出的对数似然值(Log Likelihood, LogL),Vuong和Clarke检验都可实现信息量检验程序。
表1中模型1为DD作为协变量的估计结果,模型2~4分别为Bharath和Shumway所采用的变量,Crosbie和Bohn所指出的3个决定要素以及DD拆分后的变量估计的结果,模型5~7分别在模型2~4的基础上加入了DD变量。根据模型1,DD与企业发生财务困境的可能性显著负相关,表明DD对企业财务困境有显著的预测作用。由exp(β)可知,DD每增加一个单位,企业发生财务困境的风险率将下降37.19%(exp(-0.465)-1=-0.3719)。 只是模型的PseudoR2非常低(还不到0.1),这意味着上市公司陷入财务困境风险的样本外变异多是由违约距离以外的因素所驱动的[4]。
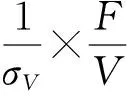
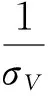
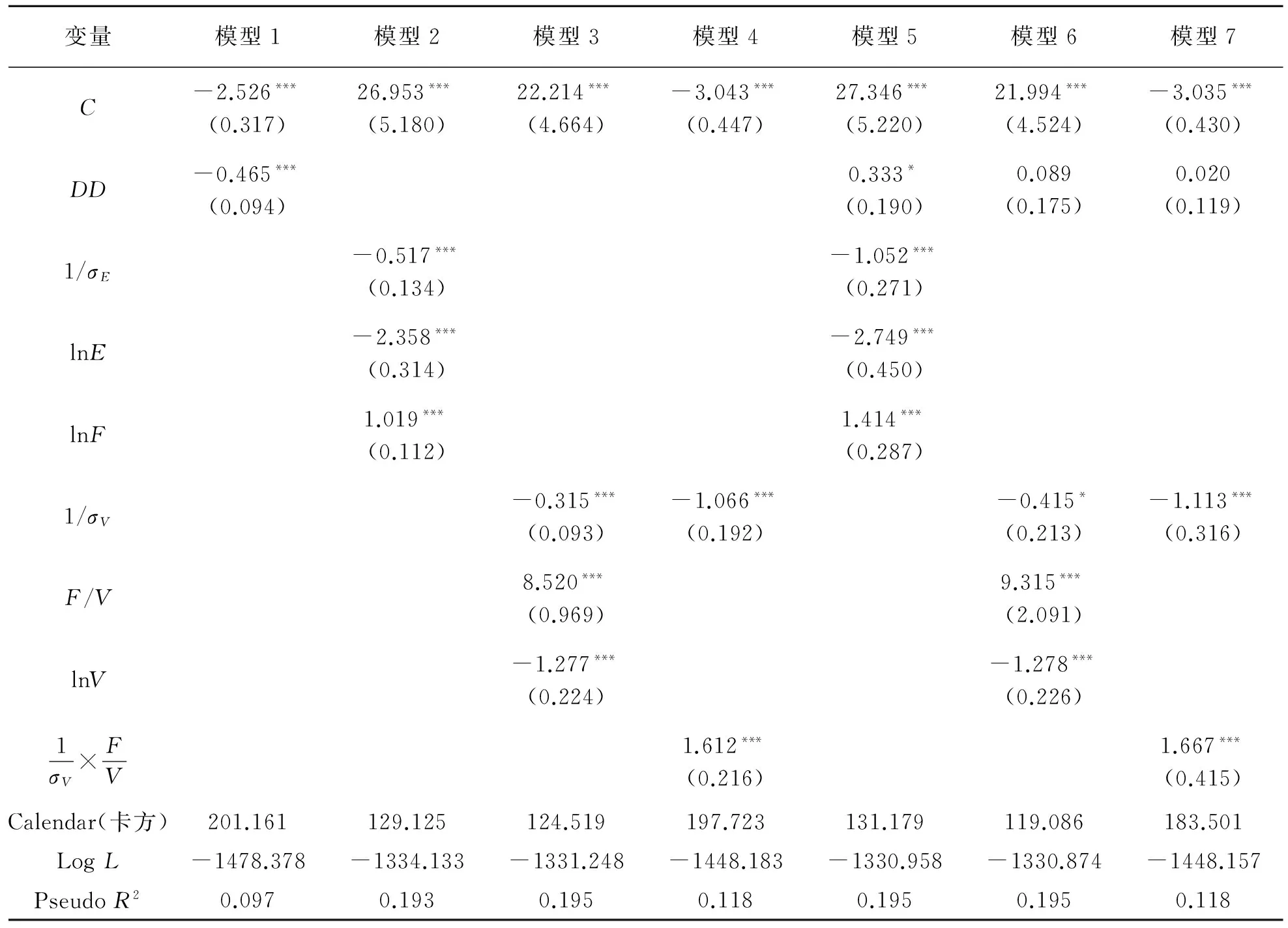
表1 模型估计
注:所有模型中都加入了公司进入时间Calendar变量,以允许基准风险率随时间的变化而变化,C为Calendar=2013年时的系数;为节省篇幅,只报告了Calendar总的卡方值;***为1%水平上显著,*为10%水平上显著。
总体上,模型2~4估计所给出的检验统计量LogL和PseudoR2都要大于模型1,尤其是模型2和3的PseudoR2都在0.19以上(0.193和0.195),是模型1的2倍。未报告的Vuong和Clarke检验证实模型2~4都在1%的统计水平上显著优于模型1。也就是说,模型2~4中的变量组合都比DD本身包含了更多与企业陷入财务困境有关的信息,这就表明DD的显著解释力与其函数形式并没有必然的联系。DD的非线性函数形式过于概括和简化了与企业财务困境有关的信息,反而不如其构成变量简单的线性组合的解释力。
5.2 十分位预测
十分位预测方法能够捕获一个模型预测财务困境的能力,并对竞争性的模型进行排序[15]。运用该方法时,需要基于一个特定的预测变量将观测数据按照十分位数分成十等分,然后计算每个十分位数中的财务困境公司数占总的财务困境公司数的比例。一个较好的预测模型,处在最前端的十分位数(第1个分位数)应有最高的预测能力,而如果一个模型没有预测能力,则其在每一个十分位数上预测出的财务困境公司比例都为10%。采用十分位预测方法的优势在于可将企业发生财务困境风险的等级按照十分位数进行排序而无需估计实际的财务困境发生概率[6]。
表2给出了基于模型预测概率排序的十分位预测结果。表中显示,在第1个十分位数组上,模型2~4分别预测出了47.31%、46.41%和35.63%的财务困境公司,不仅显著大于没有预测能力假设下10%的比例,而且还都要大于DD的单独作用所预测出的财务困境公司比例(34.73%)。在前3个十分位数组上,模型2和3累计预测出的财务困境公司比例都在75%左右,模型4所预测出的财务困境公司数虽然不到70%(68.26%),但也要略大于DD的单独作用的预测力(67.07%)。未报告的各模型累计占比折线图显示模型1和4几乎重合,而模型2和3的图形位置则一直高于模型1和4,直观地显示出DD的预测能力同资产波动率对企业财务困境的直接和间接作用的等同性,而且简单组合的各组变量的预测能力要明显大于DD这一个综合指标的单独作用。
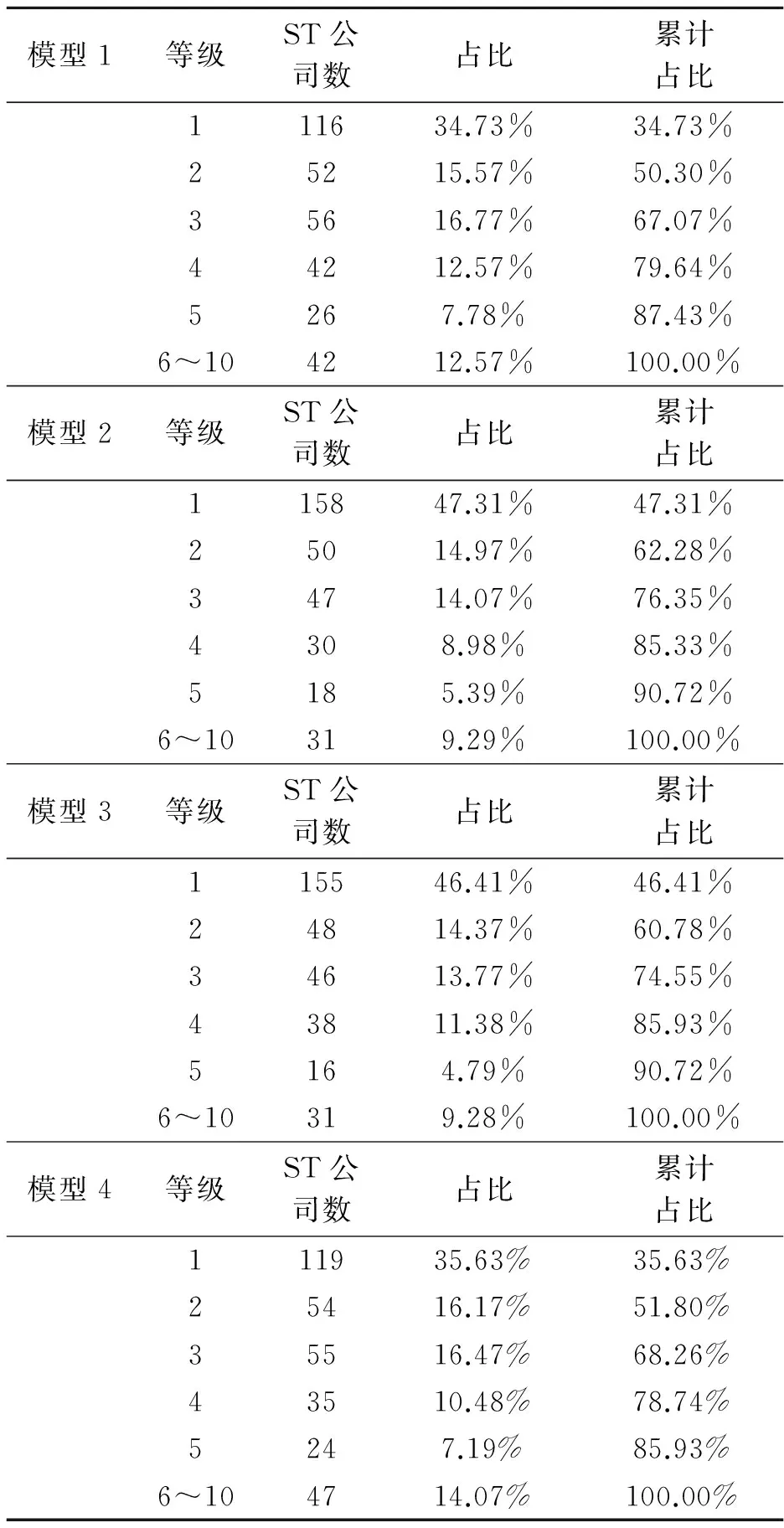
表2 各模型十分位预测的结果
由此可见,无论将DD看作是哪些关键要素的综合度量,它的表现都不如这些变量的简单组合,DD并没有完全涵盖其构成要素所要表达的信息,也就意味着Merton DD模型所提供的函数形式相对于其构成要素而言并不是最重要的,DD的显著预测力与其函数形式并没有必然的联系。我们得到的这一实证结果并不支持Bharath和Shumway的研究。可能的原因大概在于Bharath和Shumway采用Pdef为核心指标,并利用Cox模型进行模型估计,而我们采用违约距离为核心指标,依据离散时间风险模型进行估计和预测。
总之,在中国股票市场上,找不到足够的证据来支持Bharath和Shumway的结论。对于中国上市公司而言,DD虽然是高度显著的预测变量,但却过于概括和简化,反而遗漏了一些重要信息,构成DD的各变量的简单组合都比DD本身有更高的预测能力。
需要特别指出的是,由于样本观测期较长,一些重大事件(如会计准则的变化、金融衍生品的爆炸性增长等)会影响模型的稳健性[16]。为此,我们分别以股权分置改革启动年份和金融危机全面爆发年份为分界点,实证检验了以下4个观测期内的模型估计和预测结果:(1)股改前观测期:1996~2004年;(2)股改中观测期:2005~2013年;(3)危机前观测期:1996~2007年;(4)危机及后危机观测期:2008~2013年。由于各观测期的实证分析过程同整个样本观测期一样,鉴于篇幅,本文省去了这部分实证结果的报告,但实证发现同上述的结论是一致的。
6 结论
本文将上市公司被ST视为陷入财务困境,采用离散时间风险模型技术,基于1996年上市以来的非金融A股上市公司最长达18年的观测数据共16000个公司年观测值,从Merton违约距离模型的函数形式考虑,通过信息量检验和十分位预测程序,实证分析了Merton违约距离模型的预测能力,补充了现有文献对Merton违约距离模型认识不足的局面。
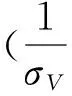
[1] Bauer J, Agarwal V. Are hazard models superior to traditional bankruptcy prediction approaches? A comprehensive test[J]. Journal of Banking & Finance, 2014, 40(3): 432- 442.
[2] 韩璐,宏伟,韩立岩.违约预测的小波结构模型研究[J].管理工程学报,2014,28(4):137-145.
[3] Altman E I. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy[J]. The Journal of Finance, 1968, 23(4): 589- 609.
[4] Hillegeist S A, Keating E K, Cram D P, et al.. Assessing the probability of bankruptcy[J]. Review of Accounting Studies, 2004, 9(1): 5-34.
[5] 石晓军,任若恩.基于期权与基于会计信息信用模型的一致性研究——对我国上市公司的实证研究[J].系统工程理论与实践,2005,25(10):11-20.
[6] Bharath S T, Shumway T. Forecasting default with the Merton distance to default model[J]. Review of Financial Studies, 2008, 21(3): 1339-1369.
[7] Crosbie P, Bohn J. Modeling default risk[R]. White Paper, Moody’s KMV, 2003. 1-31.
[8] Kumar K, Chaturvedi A. Some recent developments in statistical theory and applications[M]. Boca Raton, Florida: Brown Walker Press, 2012. 1-25.
[9] Laitinen T, Kankaanpaa M. Comparative analysis of failure prediction methods: the finnish case[J]. European Accounting Review, 1999, 19(6): 673- 678.
[10] 过新伟,胡晓.公司治理,宏观经济环境与财务失败预警研究——离散时间风险模型的应用[J].上海经济研究,2012,(5):85-97.
[11] Shumway T. Forecasting bankruptcy more accurately: a simple hazard model[J]. The Journal of Business, 2001, 74(1): 101-124.
[12] Petersen M A. Estimating standard errors in finance panel data sets: comparing approaches[J]. Review of Financial Studies, 2009, 22(1): 435- 480.
[13] Thompson S B. Simple formulas for standard errors that cluster by both firm and time[J]. Journal of Financial Economics, 2011, 99(1): 1-10.
[14] Cui Y, Cai Y L. An empirical study of financial distress prediction of listed companies in China-based on the naïve DD model of Bharath & Shumway(2008)[J]. Management Science and Research, 2014, 3(4): 118-129.
[15] Charitou A, Dionysiou D, Lambertides N, et al.. Alternative bankruptcy prediction models using option-pricing theory[J]. Journal of Banking & Finance, 2013, 37(7): 2329-2341.
[16] Beaver W H, McNichols M F, Rhie J W. Have financial statements become less informative? Evidence from the ability of financial ratios to predict bankruptcy[J]. Review of Accounting Studies, 2005, 10(1): 93-122.
Research on the Forecasting Ability of Merton Distance-to-Default Model on Corporate Financial Distress——Based on the Empirical Analysis of the Discrete-time Hazard Model
CAI Yu-lan, CUI Yi
(SchoolofBusinessManagement,SouthChinaUniversityofTechnology,Guangzhou510641,China)
Based on the functional form of Merton distance-to-default model, this paper regards the distance-to-default as an indicator of three variables, three critical factors and two split items. With the technology of the hazard model of discrete-time, we empirically analyse the forecasting ability of Merton distance-to-default model on corporate financial distress by means of the information content test and decile forecasts. We find that the nonlinear functional form of distance to default is not vital relative to its constituent indicators. The distance-to-default is too summary and abstract to include all the information so that its forecasting ability is less than a simple combination of its three groups constituent indicators. In fact, the significant predictive ability of distance-to-default comes from the direct and indirect impact of its volatility on corporate financial distress.
Merton distance-to-default model; financial distress; forecasting ability
2015- 03- 09
F272.13
A
1003-5192(2015)06- 0033- 06
10.11847/fj.34.6.33

