扩径导线在张拉载荷下的股线分层应力计算
董玉明,万建成,王 孟,司佳钧,刘 龙,杨光甫
(1.中国电力科学研究院,北京102200;2.华北电力大学 能源动力与机械工程学院,河北保定071003)
扩径导线在张拉载荷下的股线分层应力计算
董玉明1,万建成1,王 孟2,司佳钧1,刘 龙1,杨光甫2
(1.中国电力科学研究院,北京102200;2.华北电力大学 能源动力与机械工程学院,河北保定071003)
研究扩径导线分层应力计算,能够为扩径导线的应用提供技术支持。考虑扩径导线的几何特征,对扩径导线的分层应力计算进行了理论分析,推导了扩径导线分层应力计算的理论公式;建立了扩径导线的有限元模型,考虑股线间的接触非线性,对张拉载荷工况的扩径导线进行了分析;将理论计算与有限元仿真计算的结果进行了对比研究。研究结果表明:张拉载荷下扩径导线分层应力计算的理论公式与有限元结果的对比基本吻合;张拉载荷作用下,扩径导线各绞层股线所受轴向拉力从内向外逐渐减小,钢芯所受轴向应力相对较大,铝绞层所受轴向应力较小。
扩径导线;分层应力计算;张拉载荷;有限元
0 引言
随着国民经济的发展,电能需求日益增长。为提高电能输送,输电电压等级逐渐提高。当电压等级高于220 kV时,线路电抗较大,电晕损耗较为严重[1],这会提高输电线路运行成本。另外,较为严重的电晕带来较大电磁噪声,给周边环境带来噪音污染[2]。为了造就资源节约型与环境友好型的架空输电线路工程,需要选用更经济与环保的架空输电线路,扩径导线应运而生[3,4]。扩径导线通过支撑层铝线疏绞的方式扩大了导线外径,这样可以减小导线表面的电场强度和电晕放电,降低噪声,减少对无线电的干扰。相对于常规导线,扩径导线重量较轻,在满足输送容量要求和环境保护指标的前提下,可降低线路整体造价[5,6]。
由于扩径导线支撑层铝线疏绞,在外载荷作用下其各层线股的受力与普通导线有所不同。若铝股所受应力过大,则将大大降低其疲劳寿命,所以有必要分析其在平均运行张力下扩径导线分层应力。有关导线结构应力计算的研究方法主要可分为理论推导与数值仿真两种[7~11]。研究扩径导线分层应力计算,能够为扩径导线的应用提供技术支持。
本文考虑扩径导线的几何特征,对扩径导线的分层应力计算进行理论分析,推导扩径导线分层应力计算的理论公式;建立扩径导线的有限元模型,考虑股线间的接触非线性,对张拉载荷工况的扩径导线进行分析,并将理论计算与有限元仿真计算的结果进行对比研究。
1 理论分析
1.1 股线所受沿导线轴向的力
截取扩径导线的一微段进行受力分析,如图1所示。F为扩径导线所承受的轴向拉力;Zd,L为所研究股线沿自身轴线切线方向承受的拉力;Fd,L为股线沿绞线轴向方向的分力;股线螺旋角为βL。

图1 螺旋微元段受力图
股线沿自身轴线切线方向拉力为:
(1)
则扩径导线所承受的拉力:
(2)
根据轴向应力关系可知
(3)
式中:εL是指股线沿自身轴向应变。设扩径导线整体的轴向应变为ε。图2所示为股线沿自身轴向变形及扩径导线轴向变形间的关系。
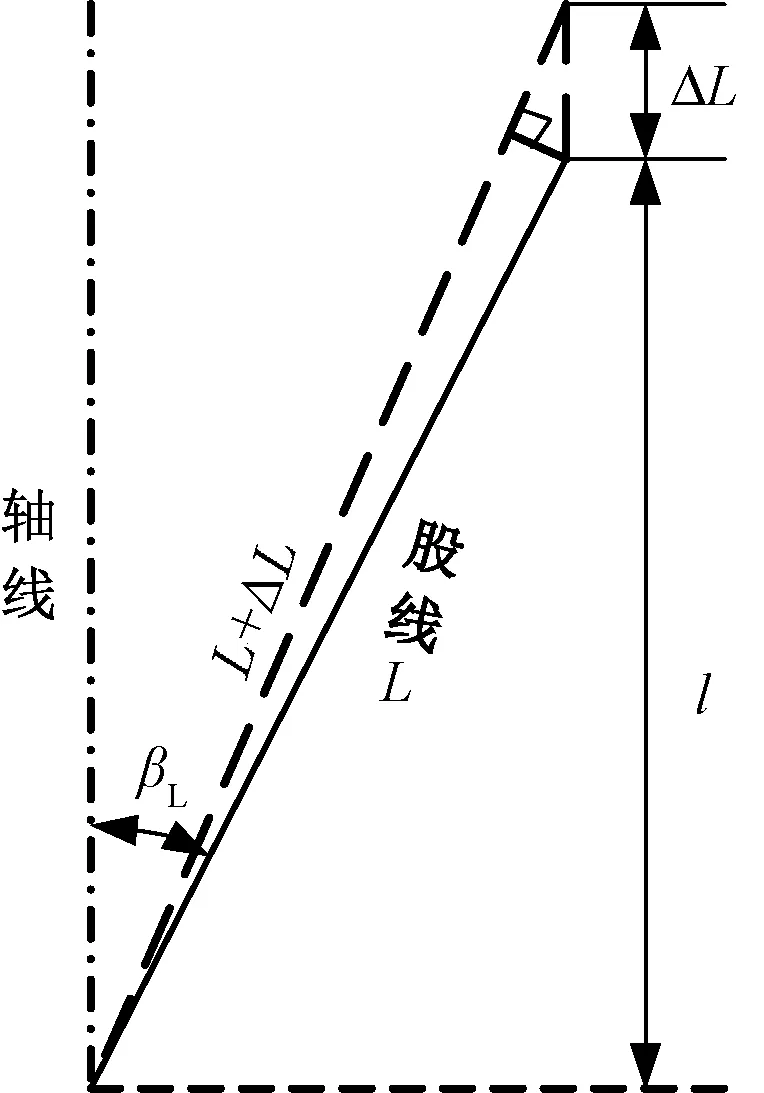
图2 股线的几何变形关系
由于
(4)
而考虑到应变很小,则有
(5)
股线沿自身轴向应变满足
(6)
由式(4)、(5)、(6)可得
(7)
则式(3)可化为
(8)
联立式(2)、(8)可得
(9)
由式(1)与(9)可知,当钢绞线承受轴向力F时,股线截面沿绞线轴向方向的分力为
(10)
1.2 股线截面应力
由于外力沿扩径导线轴向施加,其作用点可认为是绞线截面中心点上,因而计算各螺旋股线截面上内力分布时,还得考虑轴向力平移到各股线截面中心引起的弯矩作用,如下图3(a)所示。
螺旋股线层内股与股间相互作用力较小,而螺旋股线与中心股线间的摩擦也对螺旋股线产生弯矩,且与螺旋股线所承受因外力引起的弯矩的方向共线,故其总弯矩示意图如图3(b)所示。
螺旋股线截面承受的是拉弯组合,截面上的应力为
(11)
根据螺旋股线截面上的内力可得该截面上的综合应力分布,如图3(c),轴向应力的极值存在于螺旋股线椭圆截面短轴的两端。
中心股线轴线与绞线轴线重合,所受外力与其轴线共线,因而其只承受拉伸应力。由此可知,钢绞线内中心股线仅承受拉伸载荷,截面上为均布正应力;螺旋股线承受拉弯载荷,截面上存上拉伸应力与弯曲应力,其截面法向应力沿椭圆短轴线性变化,极值位于短轴两端。

图3 螺旋股线截面内力平衡图
2 有限元仿真
为验证分层应力计算理论分析的正确性,以JLXK/G1A-530(630)/45扩径导线为例,利用Ansys软件采用有限元方法进行分析验证。JLXK/G1A-530(630)/45扩径导线的截面如图4所示,其主要参数如表1所示。
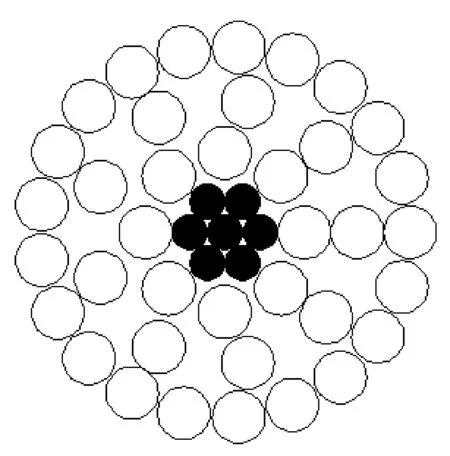
图4 扩径导线的横截面结构
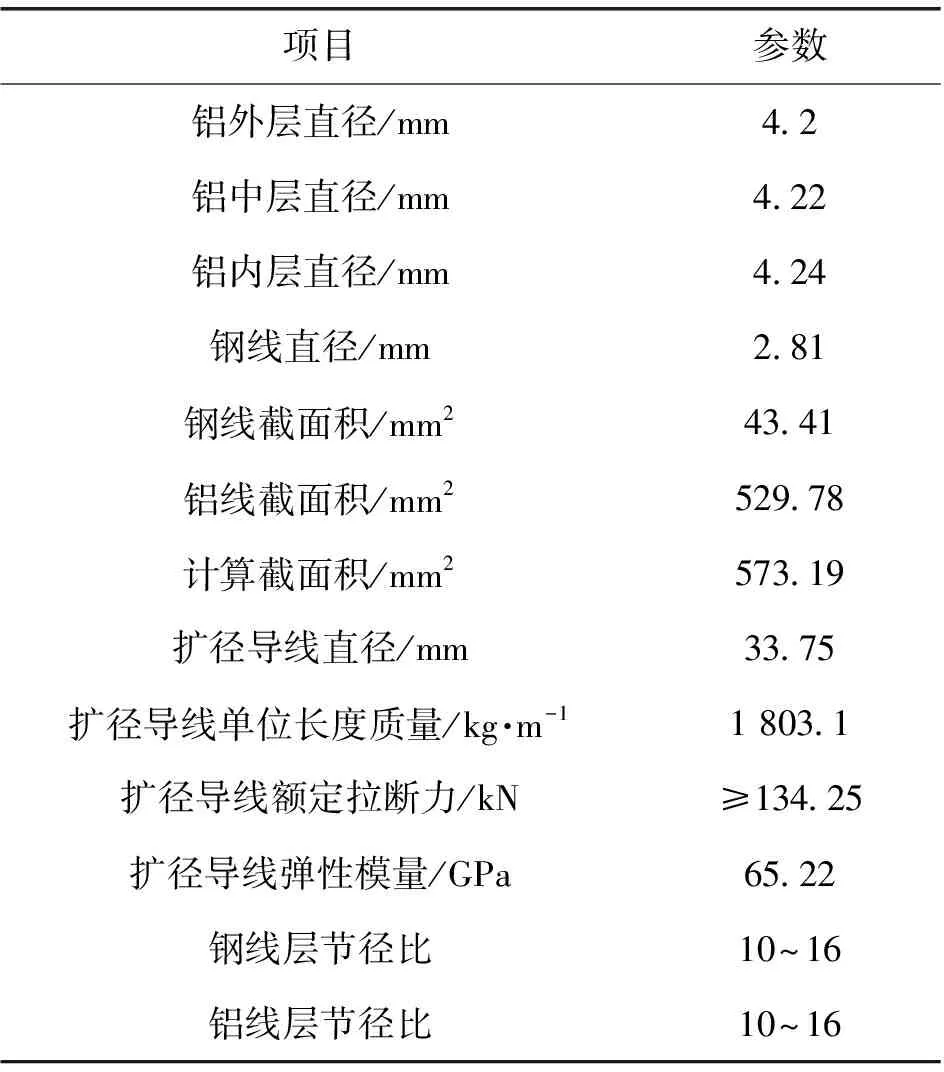
表1 扩径导线的主要参数
2.1 有限元模型
这里采用实体模型模拟扩径导线,考虑到在外载荷作用下股线间的接触、弹塑性变形等问题,计算模型具有强非线性,因此选用8节点的Solid185非线性单元。在计算过程中需要考虑股线间的接触问题,这里选用接触的目标单元为TARGE170,接触单元为CONTA174。采用参数化建模方法建立扩径导线的有限元模型如图5所示。在计算时,导线的一端固定,另一端设为刚性平面并施加轴向拉力。

图5 扩径导线有限元模型
考虑到扩径导线线股在接触位置会发生塑性变形,因此扩径导线建模过程采用双线性等向强化模型,钢股线其弹性模量E=206 GPa,泊松比μ=0.3,材料密度为ρ=7.85×103kg/m3,屈服极限为σ=1 100 MPa,铝股线其弹性模量E=60 GPa,泊松比μ=0.3,材料密度为ρ=2.7×103kg/m3,屈服极限为σ=170 MPa。
2.2 有限元分析结果
施加张拉荷载为线路的平均运行张力,等于25%RTS。加载计算后,得到扩径导线轴向应力云图如图6所示。

图6 张拉载荷作用下轴向应力云图
由于端部约束及加载端刚性面的影响,距模型两端部分应力失真,故距固定端一定距离截取3个截面,其轴向应力云图如图7所示。
扩径导线各层股线轴向应力分布如图8所示。从图中可以看出:接触区域有应力集中现象,轴向应力一般沿股线椭圆截面短轴向外侧逐渐减小。

图7 张拉载荷作用下各截面轴向应力云图
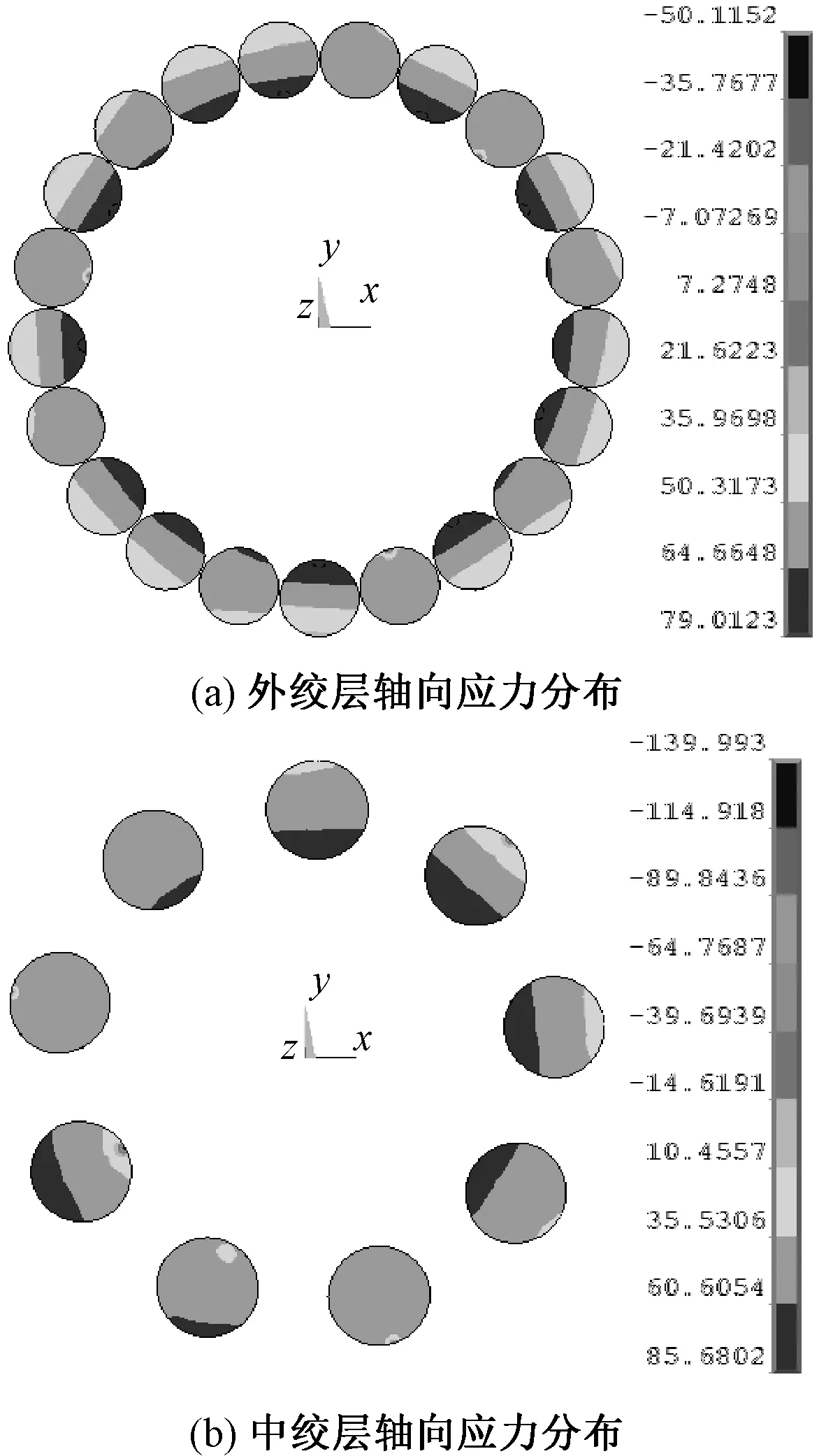

图8 张拉载荷作用下某截面内各绞层截面轴向应力云图
3 分层应力计算结果对比
为减小边界条件对分析结果的影响,取扩径导线模型的中间截面,通过对截面轴向应力的积分,求出每个绞层内各根股线的截面轴力,求出每个绞层内股线截面的平均轴向应力,并与理论值进行对比,如表2所示。
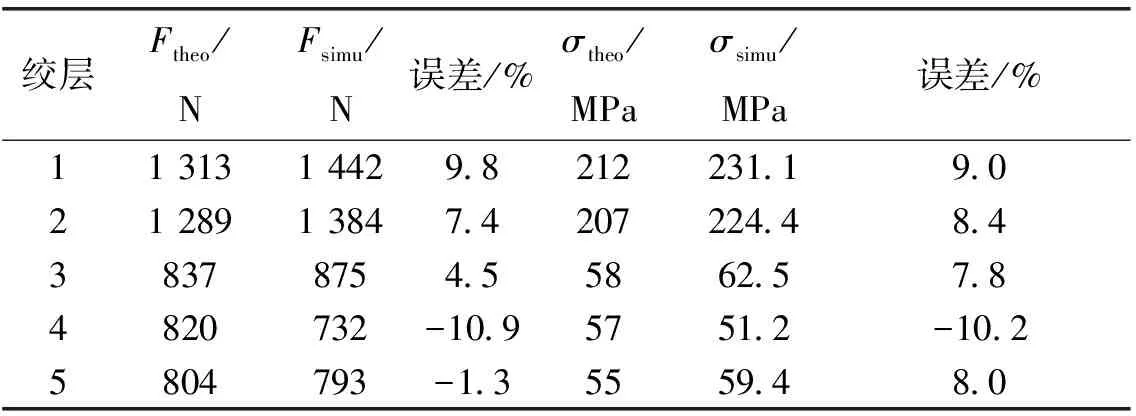
表2 各股线截面内力的理论值与有限元值对比
由表2可知,各股线轴力理论值与仿真值最大相差为10.68 %,最小相差为1.34 %,而该截面积分总轴向力为39.998 kN,与总荷载相等。平均应力理论与仿真值相差在7%~10%之间。理论推导过程,未考虑相临绞层间的摩擦,由此表可知,绞层间的接触对各股线间的轴力存在一定的影响。张拉载荷作用下,扩径导线横截面内绞层轴向应力从内向外逐渐减小,钢芯相对较大,铝绞层轴向应力较小,且铝绞层间彼此相差不大。
4 结论
(1)建立了扩径导线分层应力计算的理论公式,该公式计算结果与有限元仿真结果基本吻合。
(2)建立了扩径导线的分层应力计算有限元模型,并进行了分析。分析结果表明:各股线接触区域有应力集中现象,轴向应力一般沿股线椭圆截面短轴向外侧逐渐减小。
(3)在线路平均运行张拉载荷作用下,扩径导线内绞层各股线所受轴向拉力从内向外逐渐减小;中心股线轴向应力相对较大,铝绞层轴向应力较小,且铝绞层间彼此相差不大。
[1]隋晓杰,宋守信.高压输电线路电晕放电分析[J]. 电力建设, 2006, 27(3): 37-38.
[2]叶鸿声,袁志磊,赵连岐.降低特高压输电线路电晕可听噪声的措施[J]. 电力建设, 2007, 28(8): 1-5.
[3]刘本粹, 喻新强, 郭日彩, 等. 扩径导线在超高压大容量输电工程中的应用展望[J]. 电网技术, 2007, 31(21): 1-4.
[4]张禄琦,郝阳,李小亭,等.扩径导线在特高压交流输电线路工程中的应用[J]. 电力建设, 2012, 33(8): 1-4.
[5]万建成,刘臻,孙宝东,等. 扩径导线的分类与扩径方式的选择[J]. 电力建设,2010, 31(6):113-118.
[6]万建成,司佳钧,刘彬,等. 一种结构稳定的大截面扩径导线设计[J]. 电力建设,2013, 34(10):92-96.
[7]赵新泽,周权,高伟.钢芯铝绞线同层线股间接触有限元分析[J]. 三峡大学学报(自然科学版),2011,33(1):69-72.
[8]Gnanavel B K, Parthasarathy N S. Effect of Interfacial Contact Forces in Lateral Contact Wire Strand[C]. World Congress on Engineering 2011(WCE 2011), Lodon, UK, 6-8 July, 2011: 2057-2063.
[9]Jolicoeur C, Cardou A. Semicontinuous Mathematical Model for Bending of Multilayered Wire Strands[J]. Journal of Engineering Mechanics, 1996, 122(7): 643-650.
[10]马行驰, 何大海, 朱瑞. ACSR-720/50 型架空导线单股应力状态分析[J]. 电线电缆, 2013,(3): 13-16.
[11]姚瑞, 黄新波. 架空导线的有限元建模方法解析[J]. 科技资讯, 2013 (24): 103-104.
Stress Calculation of Between Layered Strands of Expanded Conductor Under Tension
Dong Yuming1, Wan Jiancheng1, Wang Meng2,Si Jiajun1, Liu Long1, Yang Guangfu2
(1.China Electric Power Reseach Institute, Beijing 102200, China; 2. Department of Mechanical Engineering,North China Electric Power University, Baoding 071003,China)
This study about expanded conductor stratified stress calculations could provide technical support for the production and application of the expanded conductor. First, considering the geometric characteristics of expanded conductor, the theoretical analysis of stratified stress calculation of expanded conductor was done and the theoretical formula for stratified stress calculation was deduced. Then, a finite element model of expanded conductor was developed and the tensile load condition was studied, considering the nonlinear contact of the strands. Finally, the results of the theoretical calculations were compared with those of the finite element simulation. The results showed that the results of the theoretical formula for stratified stress calculation of expanded conductor were basically consistent with those in the simulation. Under the tensile load, the axial tension in each layer of expanded conductor decreased from the inside to the outside, and the inner strands made of steel withstood larger force while the aluminum layer’s axial tension was weaker.
expanded conductor; stratified stress calculation; tensile load; FEM
2015-05-08。
国家电网公司科技项目(GCB17201400076)
董玉明(1968-),男,高级工程师,从事导线、金具研究与设计工作,E-mail:dongyuming@epri.sgcc.com.cn。
TM73
A
10.3969/j.issn.1672-0792.2015.07.012

