不确定策略对发电侧定价的激励机制研究

韦加雄，昌 健，王莉芳，李强，董稳改

(1.国网陕西省电力公司 营销部，陕西西安710048； 2.西北工业大学 管理学院，陕西西安710100)

不确定策略对发电侧定价的激励机制研究

韦加雄1，昌 健2，王莉芳2，李强2，董稳改2

(1.国网陕西省电力公司 营销部，陕西西安710048； 2.西北工业大学 管理学院，陕西西安710100)

现有的对电力市场的研究以确定策略下的寡头博弈模型为主，但这种确定策略框架却不符合现实中寡头厂商会改变策略的情形。建立了不确定策略框架下的Bertrand双寡头模型，对其数值仿真并将结果与确定策略框架下的模型进行比较。结果表明发电厂商采用不确定策略能带来比采用确定策略更多的利润，且能保证电价的稳定。说明让各企业采取自己合适的策略竞争可以提高市场效率。

Bertrand双寡头模型；不确定策略；数值仿真；市场效率

0 引言

随着电力基础设施的不断完善，我国的电力市场正在逐渐地从卖方市场向买方市场过渡[1]。随着市场机制的引入，电力市场也将从自由竞争阶段发展到寡头垄断阶段。由于电力市场的复杂性，学者们开始使用混沌理论研究电力市场的性质[2,3]。文献[4]提出了联营模式下的新模型来模拟寡头市场的行为，并与传统模型进行了比较。文献[5]基于寡头垄断的古诺模型推导求解发电市场在不同交易模式下的市场均衡解，对结果进行比较分析。文献[6]介绍了PJM电力市场"三寡头垄断测试法"的基本原理和方法，为电力市场的有效运行及监管制度的建设完善提供参考。文献[7]综述了博弈论在发电市场中的应用。

目前的研究中均是基于固定策略下的寡头模型，该假设意味着厂商在决策的时候只采取一个策略。然而在实际中，厂商的决策不会固定不变，因此基于该假设得到的模型难以模拟现实世界的情形。本文将市场上的发电厂商抽象为两类，在不确定策略的框架下建立Bertrand双寡头模型，并和确定策略框架下的模型进行比较。

1 确定策略下的发电侧定价模型

1.1 模型的建立

通常，博弈模型中厂商采取的策略有三：单纯策略、有界理性策略和适应策略[8]。实际上，适应策略是单纯策略和有界理性策略的一个折中，即适应策略的两个极端情形分别是单纯策略和有界理性策略。为简单起见，本文只考虑单纯策略和有界理性策略。

考虑线性的供求函数[9]：

Qi=ai-bipi+dipj

式中：ai>0,bi>0,di>0(i,j=1,2;i≠j)；参数di表示厂商j生产产品对厂商i生产产品的替代效应。设成本函数如下：

Ci=ciQi,i=1,2

式中：ci是厂商i生产产品的边际成本。于是厂商i的利润函数为：

πi(p1,p2)=(pi-ci)Qi,i=1,2

厂商i在t+1时刻的边际利润是：

其中i,j=1,2;i≠j。

厂商1采取“单纯策略”[8]，即

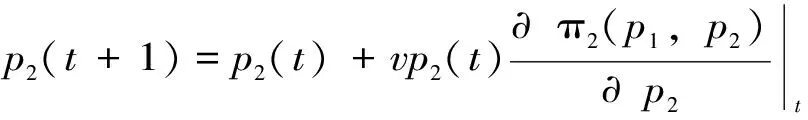
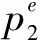
1.2 模型的仿真

引入总利润指标[10]来刻画模型(1)的不同状态对发电厂商利益的影响：

(2)

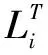
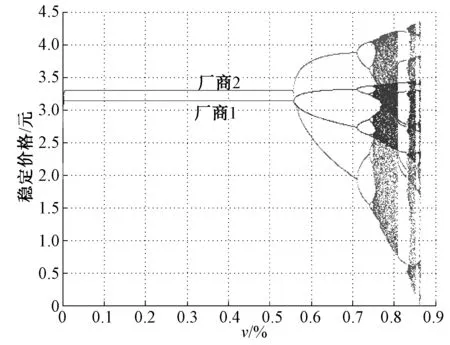
图1 模型一的分岔图

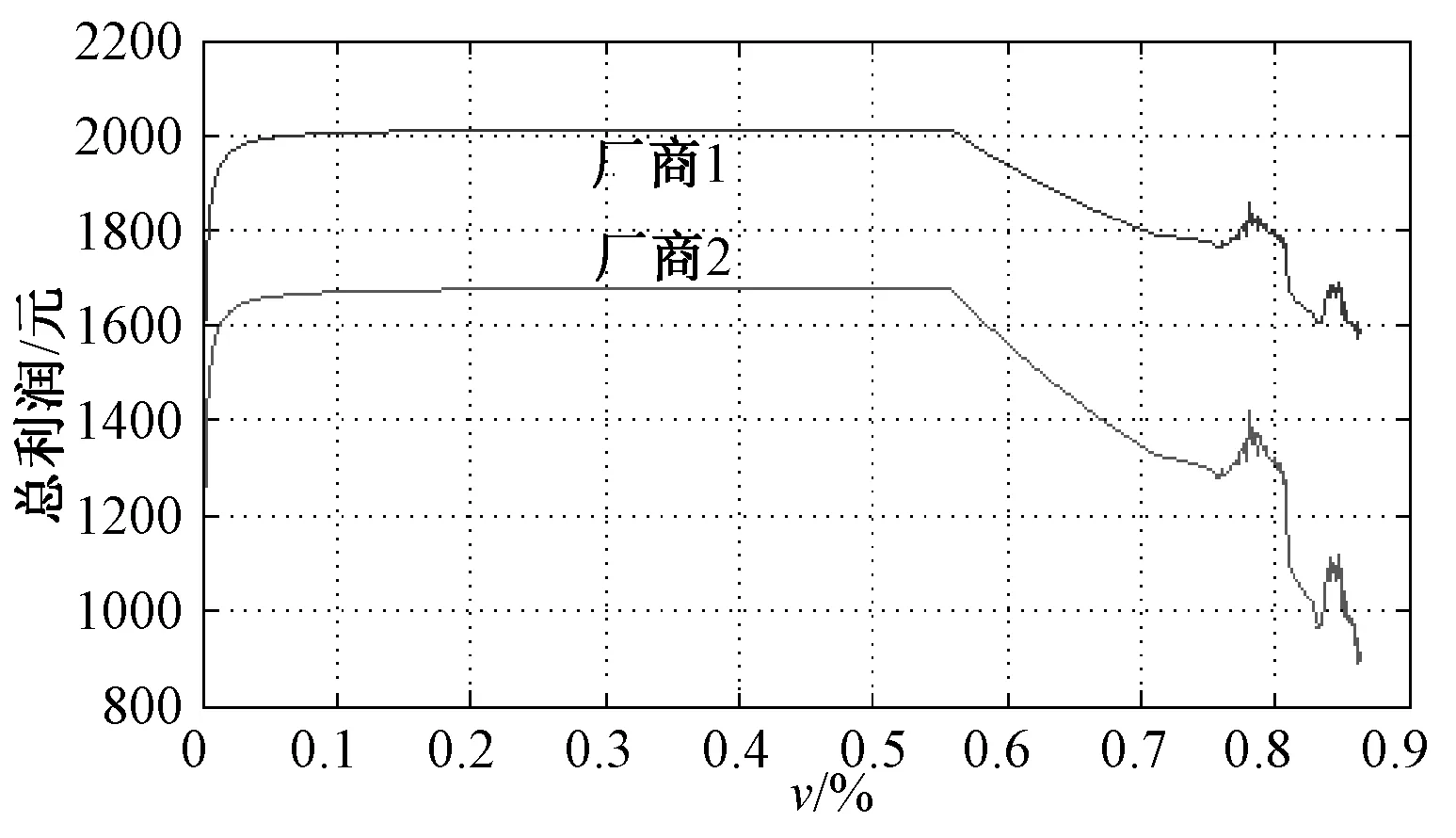
图2 模型一的总利润图

由以上的数值结果可以得到如下结论：对于确定策略下的异质Bertrand双寡头模型而言，随着“有界理性”厂商调节自身产品价格速率的变化，该博弈模型会出现分岔，混沌等复杂的动力学行为，两个厂商的总利润也会随着减少。这意味着在现实中，厂商之间会不断调整价格而进入激烈的价格战，致使厂商们的总利润减少，不利于市场健康、稳定地发展。

2 不确定策略下的发电侧定价模型

2.1 模型的建立

发电厂商制定策略是基于自身在市场中的位置，然而地位不是一成不变的，因此厂商的策略也可能发生变化。因此本文建立了基于不确定策略的Bertrand双寡头模型，在此模型中，两个厂商都可以采用“单纯策略”和“有界理性策略”，具体采用哪个策略将依据各自的收益矩阵来确定。

基于确定模型一，得到以下不确定模型：

(3)

记“单纯策略”为策略1，“有界理性策略”为策略2。式中的Sij(i,j=1,2)表示厂商i采取了策略j，pij(t+1)表示t+1时刻Sij条件下厂商i的价格，pi(t+1)表示t+1时刻厂商i做出决策(判断采用策略1还是策略2)后的价格。

假设博弈双方均知道对方的策略集，因此有供求关系：

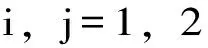
(4)

记策略组合厂商1采取策略i，厂商2采取策略j为Rij，则Q1ij(t+1)，Q2ij(t+1)分别表示t+1时刻厂商1，厂商2在Rij下的产量。进而有利润函数为：

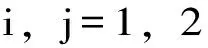
(5)

式中：l1ij(t+1)，l2ij(t+1)分别表示t+1时刻厂商1，厂商2在Rij下的利润。

博弈双方的收益表如表1所示。

表1 模型收益表

厂商1的收益表中，每一列的较大者记为1，较小者记为0；厂商2的收益矩阵中，每一行的较大者记为1，较小者记为0。点(1,1)是该博弈的纳什均衡点。若收益表没有均衡点，则厂商1和厂商2将不断博弈下去而达不到均衡状态。

2.2 模型的仿真

利用Matlab进行数值仿真，得到图3、图4。图3显示的是模型三的分岔图，a1=a2=2,b1=b2=0.5,c1=0.3,c2=0.7,d1=d2=0.3。此时没有分岔。图4显示的是两个厂商的总利润图，参数条件同图5，博弈时域T=500。此时两厂商的总利润均是稳定的。而且不确定模型三的总利润高于确定模型一的，具体说来，模型三中，厂商1的总利润为2013，厂商2的总利润为1678.9；模型一中，厂商1的总利润为1976，厂商2的总利润为1666.0。

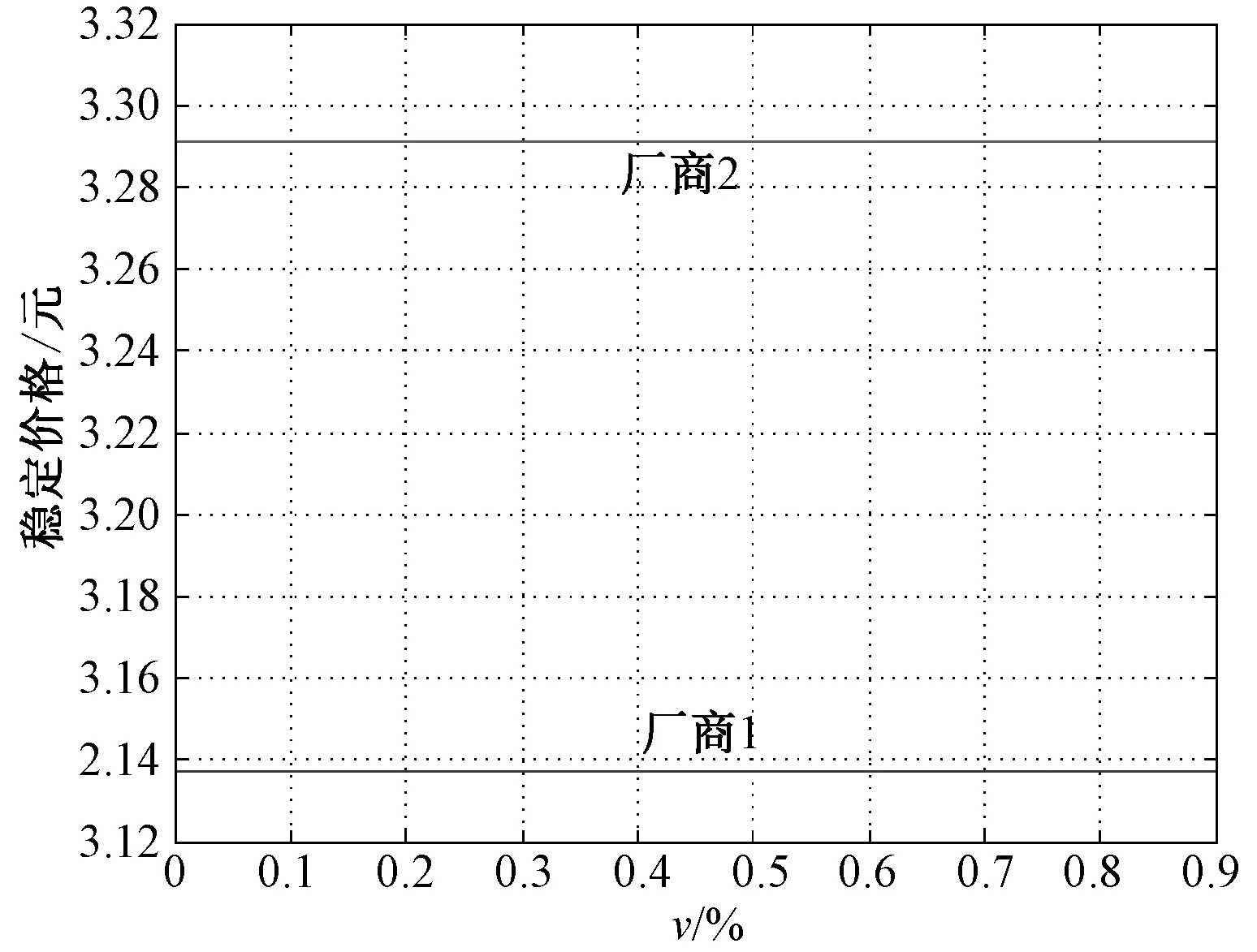
图3 模型三的分岔图，参数条件为

图4 模型三的总利润图

综上所述，与确定模型一不同，不确定模型三没有分岔，混沌等复杂的动力学行为，厂商之间的博弈可以到达纳什均衡，而且此时厂商各自的利润都要高于确定模型中相应的利润。这说明厂商对策略的选择不仅可以保护自身利益，而且可以消除厂商之间的恶性竞争，使市场平稳、健康地发展。本文从演化博弈论的角度解释了厂商调整自身策略的动机，与现实世界相符。

3 结论

本文研究的是放开电力价格管制后，一个双寡头电力市场的博弈行为。当这两个发电厂商采取确定策略的时候，它们可能会遇到激烈的价格战，且市场上会出现电价剧烈波动的现象；当这两个发电厂商采取不确定策略的时候，市场的电价反而会趋于稳定，且此情形下两个发电厂商的利润均高于它们采取确定策略时的利润。这说明不确定策略不仅可以帮助厂商获得更高的利润，也可以消除厂商之间的恶性竞争，保护市场的电价稳定。亦即证明了让各企业采取自己合适的策略竞争可以提高市场效率。

[1]杨树, 梁樑, 熊立. Cournot和Bertrand竞争下均衡质量的比较[J]. 系统管理学报, 2008，17(1):104-109.

[2]何洋,邹波,李文启,等.基于混沌理论的电力系统短期负荷预测的局域模型[J].华北电力大学学报(自然科学版),2013,40(4):43-50.

[3]张锁魁.基于Matlab/Simulink含风电的电力系统混沌特性研究[J].电力科学与工程,2014,30(7):27-31.

[4]袁智强,邓超平,蒋传文,等. 电力寡头垄断市场的均衡分析[J]. 继电器,2004,32(5):7-10，28.

[5]王宇飞. 发电侧寡头垄断市场的均衡分析[J]. 陕西电力,2007,35(4):12-15.

[6]张夏平,宋依群,杨立兵,等. PJM电力市场三寡头垄断测试法[J]. 华东电力,2008,36(5):23-25.

[7]武永军,赵飞.综述博弈论在发电市场中的应用[J].农村电气化,2013,(S1):37-40.

[8]Elabbasy E M, Agiza H N, Elsadany A A. Analysis of nonlinear triopoly game with heterogeneous players[J]. Computers and Mathematics with Applications, 2009, 57(3): 488-499.

[9] 于维生,于羽. 基于伯川德推测变差的有限理性动态寡头博弈的复杂性[J]. 数量经济技术经济研究,2013,30(2):126-137.

[10]Du J G, Huang T W, Sheng Z H, et al. A new method to control chaos in an economic system[J]. Applied Mathematics and Computation, 2010, 217(6): 2370-2380.

Incentive Mechanism of Uncertain Strategy to Generation-side Pricing

Wei Jiaxiong1, Chang Jian2, Wang Lifang2, Li Qiang2, Dong Wengai2

(1. Department of Marketing, Shanxi Province Electric Power Company of State Grid, Xi’an 710100, China; 2. School of Management, North Western Polytechnical University, Xi’an 710100, China)

Recent studies on electric market are mainly based on certain-strategy framework, but a framework like this does not go with the fact that the oligarches could change their strategy. A Bertrand duopoly model is set up in an uncertain-strategy framework, numeric simulation is implemented and comparison is made with the counterpart in the certain-strategy framework. Result shows that uncertain strategy could lead more profits and a stable electric price compared with certain strategy, which demonstrates a suitable strategy could enhance market efficiency of a firm.

bertrand duopoly; uncertain strategy; numeric simulation; market efficiency

2015-05-04。

韦加雄(1965-)，男，高级工程师，研究方向为电力营销。通信作者：昌健，E-mail：luyu1892@126.com。

F224.31

A

10.3969/j.issn.1672-0792.2015.07.006