风力发电系统可靠性建模与优化检修策略
秦 洋,马慧民,朱田玮,朱庆华
(上海电机学院 电气学院, 上海200240)
风力发电系统可靠性建模与优化检修策略
秦 洋,马慧民,朱田玮,朱庆华
(上海电机学院 电气学院, 上海200240)
针对风力发电系统可靠性评估及运行维护存在的问题,对双馈风力发电系统的运行原理、故障机制进行了研究,运用马尔可夫过程方法和可靠性理论建立了风力发电系统的可靠性模型,在考虑系统随机故障和老化故障的情况下,提出了一种改进型发电系统的状态检修模型,根据系统的状态转移关系得到系统的状态转移矩阵,借助MATLAB对系统的可用度进行求解并探讨了检测时间对于系统可用度的影响,最后分析得出不同发电老化系统可靠性最优时的检修策略。结果表明,该模型能有效地对发电系统可靠性进行量化评估,为制定科学合理的风机维护方案提供了理论支持。
风力发电系统;马尔可夫过程;可靠性模型;检修策略;可用度
0 引言
风能作为一种环保清洁的可再生能源,越来越受到世界各国的普遍重视,纷纷采取激励措施推动本国风电技术行业发展,近十年来全球装机容量年平均增长率保持在25%左右,现正朝着大容量、高质量的海上风电机组的方向发展。随着风电机组装机容量的不断提高,风电机组的结构也越来越复杂,伴随机组运行环境的恶劣,致使风力发电系统的故障率居高不下,因此在追求发电容量的同时,必须考虑发电系统运行的可靠性[1]。
目前,国内外对于风电机组的研究主要集中于故障诊断和控制策略等方面[2~4],在风电机组可靠性评估和运营维护方面研究的还较少,文献[5]提出了基于马尔科夫链的风机关键部件多阶段老化模型,用成本效益分析法确立了机组的最优检修周期;文献[6]提出了基于半马尔科夫决策过程的风机多状态维修优化模型,分析各退化状态下的维修策略,用策略迭代法法确立了机组的最优维修决策;文献[7]把风机电气组件进行拆分,建立了电气组件系统的可靠性模型,并比较了不同类型风机的可靠性和发电效率;文献[8]在此基础上把风机拆分为各个子系统,建立了基于马尔可夫过程的可靠性模型,构建了机组老化全面修复维修模型。
上述文献从不同角度研究了风机状态维护优化模型,对于提高风机可靠性运行有着重要的意义,但是,所建模型中对检测状态及检测时间对系统可用度的影响考虑得还不够充分。本文在相关研究成果的基础上,进一步研究双馈风力发电系统的可靠性计算方法,建立发电系统的可靠性数学模型,深入分析发电系统故障状态和运行状态之间相互转移的过程,结合发电系统的老化过程和实际检修情况,充分考虑了检测状态以及检测时间对系统可用度的影响,利用改进的状态空间图对发电系统建立其状态检修模型,以检修间隔为优化变量,实施风力发电系统检修策略的优化。
1 发电系统主要结构及故障分析
风力发电系统结构复杂化,为便于研究分析和建模,选取对系统可靠性影响较大的发电机、变流器、电刷滑环等主要部件作为研究对象。由于风电机组通常安装在偏远郊外或海岸,运行环境极为恶劣,此外风力发电设备本身设计不当或者质量欠佳等问题,都会影响风机运行的可靠性,根据瑞典风场2000~2004年间故障数据统计表明[9],发电系统是机组中最常发生故障的系统,也是引起风机停机时间的主要原因,其故障率高达23%。双馈风力发电系统的工作原理如图1所示,风轮通过升速齿轮箱与发电机的主轴相连,感应电动机的定子端直接接入电网,转子端则通过电刷滑环连接变流器后接入电网,只有20%~30%的功率通过变流器经稳压后传入电网。
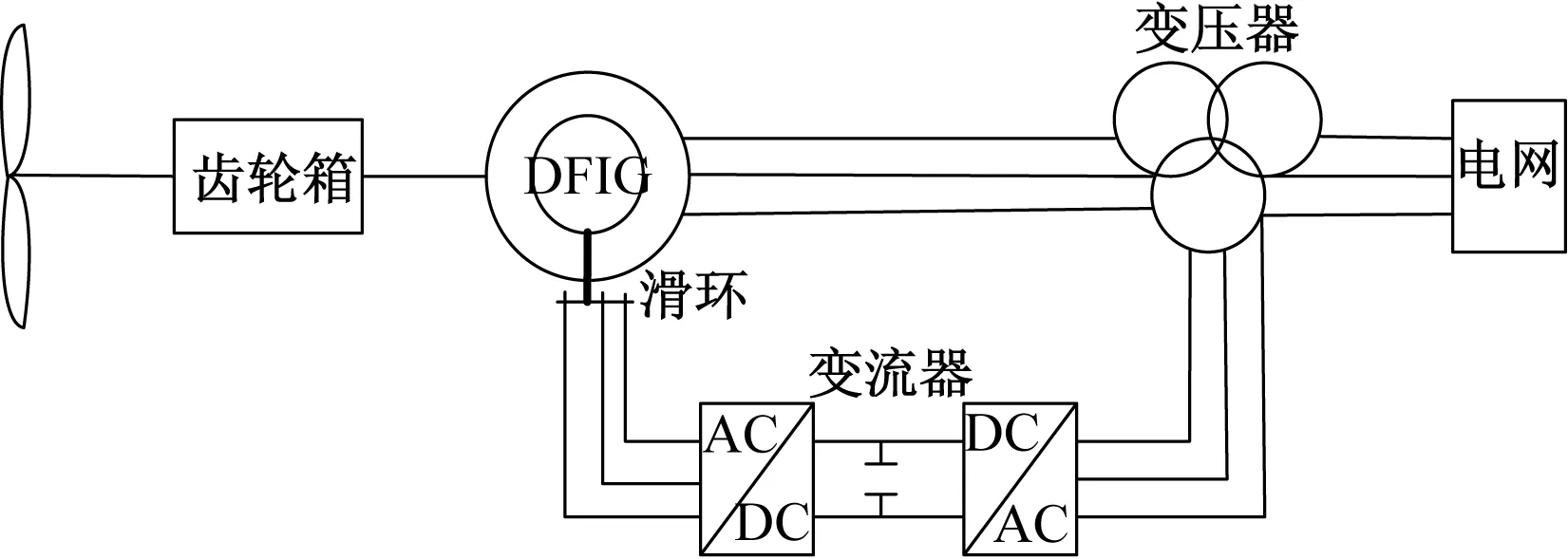
图1 双馈感应风力发电机原理图
双馈异步发电机是一种绕线式感应发电机,是变速恒频风力发电机组的核心部件,由于机组运行工况复杂、电网负荷持续变化,易使发电机温度过高、振动过大而易损坏风力发电机的轴承及绕组的绝缘,因此,故障率明显高于其他发电机,据统计异步发电机中最常发生故障的部位是轴承、定子、转子,三者的故障率分别为40%、38%、10%[10]。变流器将风机发出的电能转换为电压和频率都稳定的电能送入电网,采用变速恒频控制技术,使发电机的转速随风力大小而变化,在额定转速范围内维持最佳的叶尖速比,同时保证发电机输出电压幅值和频率与电网相同,但高温发热、电磁干扰等恶劣因素均影响变流器的工作性能,极易导致变流器故障,且故障主要发生在控制驱动单元、直流母线环节、逆变器等组件中。发电机定子端直接接入电网,而转子绕组则通过电刷和滑环与变流器相连,据统计在发电系统运行过程中,电刷和滑环之间的机械磨损会影响电机的寿命,其故障率较高,故障还将会引发电机转子侧与变流器连接故障,使部分功率无法通过转子侧馈送到电网。
2 发电系统可靠性建模
2.1 马尔可夫过程
马尔可夫过程[11]是一种基于概率统计的特殊随机过程,能够描述系统在开始运行后状态之间相互转移过程,该过程具备无后效性,即只要系统前一个状态一经决定,系统的下一个状态的概率即可确定,并与之前的状态无关。由于风电机组故障状态和修复状态之间的相互转移是一个随机过程,而马尔可夫过程能够很好描述这种随机现象,是风电机组运行状态建模的有力工具。
为了应用马尔可夫过程建立风力发电系统的可靠性模型,需要做出如下假设:(1)系统部件处于正常或故障状态,并且两种状态可以相互转换;(2)系统中部件处于正常或故障状态是互相独立的;(3)系统部件的故障率和修复率均为常数,即状态转移均服从指数分布;(4)只考虑对硬件进行可靠性分析,不考虑软件和人为因素。
2.2 发电系统的可靠性数学模型
通过对双馈风力发电系统运行原理与故障机制进行分析,发电系统关键部件之间的连接方式并不是简单的串联关系,但可以通过运用马尔可夫过程理论建立发电系统的可靠性模型[7],令发电机、变流器、电刷滑环分别简称为IG、Con、Br,则马尔可夫状态转移关系如图2所示。
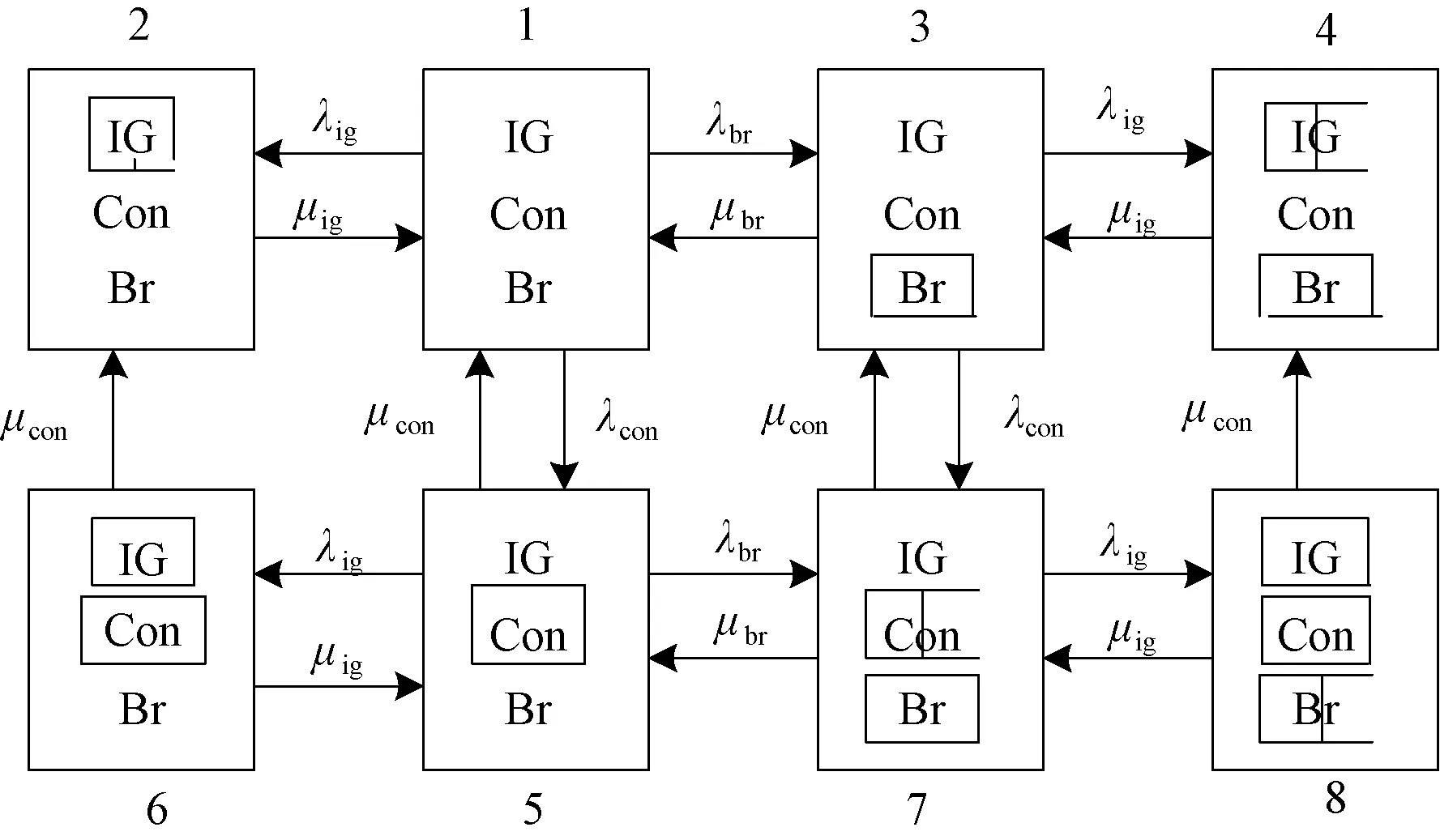
图2 发电系统的可靠性模型
图中带方框的子系统表示该部件处于故障状态,相反为正常状态,为了评估发电系统简化可靠性模型参数,最适合采用频率平衡法,根据频率平衡法:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
式中:λig、λcon、λbr分别为发电机、变流器、电刷滑环的故障率;μig、μcon、μbr分别为发电机、变流器、电刷滑环的修复率。根据风力发电系统处于故障状态或者运行状态,可以得到系统简化的可靠性模型,如图3 所示。
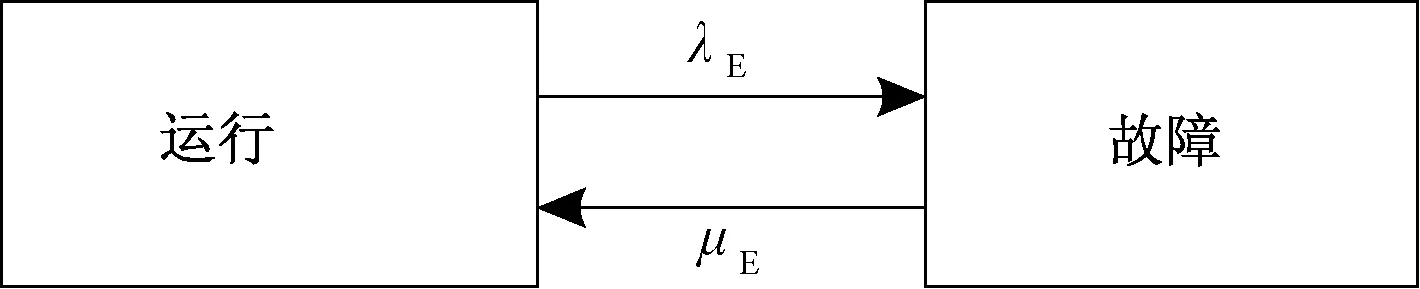
图3 发电系统简化后的可靠性模型
根据发电系统运行原理,运行状态包括图2中的状态1、状态3、状态5、状态7,其余状态为故障状态,PUp、PDn分别表示系统处于运行状态和故障状态的稳态概率,则系统的故障率和修复率如下:
(10)
(11)
(12)
(13)
3 发电系统检修优化策略
电力设备状态检修[12]是一种区别于传统的事后检修和定期检修的新型检修方式,通常以提高系统可靠度或降低设备风险水平为目标,能有效地解决传统检修中的维修不足和维修过剩带来的问题。发电系统和其他电力设备一样,在运行过程中可以分为不同的劣化状态[13],在对模型进行假设后,系统各状态之间满足马尔可夫过程的无记忆性,各状态的转移概率可以用空间状态图描述,由于经典状态图忽略了检测状态及检测时间,为了更加符合工程实际情况,结合电力设备的状态维修理论[14,15],在考虑随机故障和老化故障的情况下,提出了改进型的状态空间图,构造发电系统状态检修模型,如图4所示,得到系统可靠性最优时的维修策略。
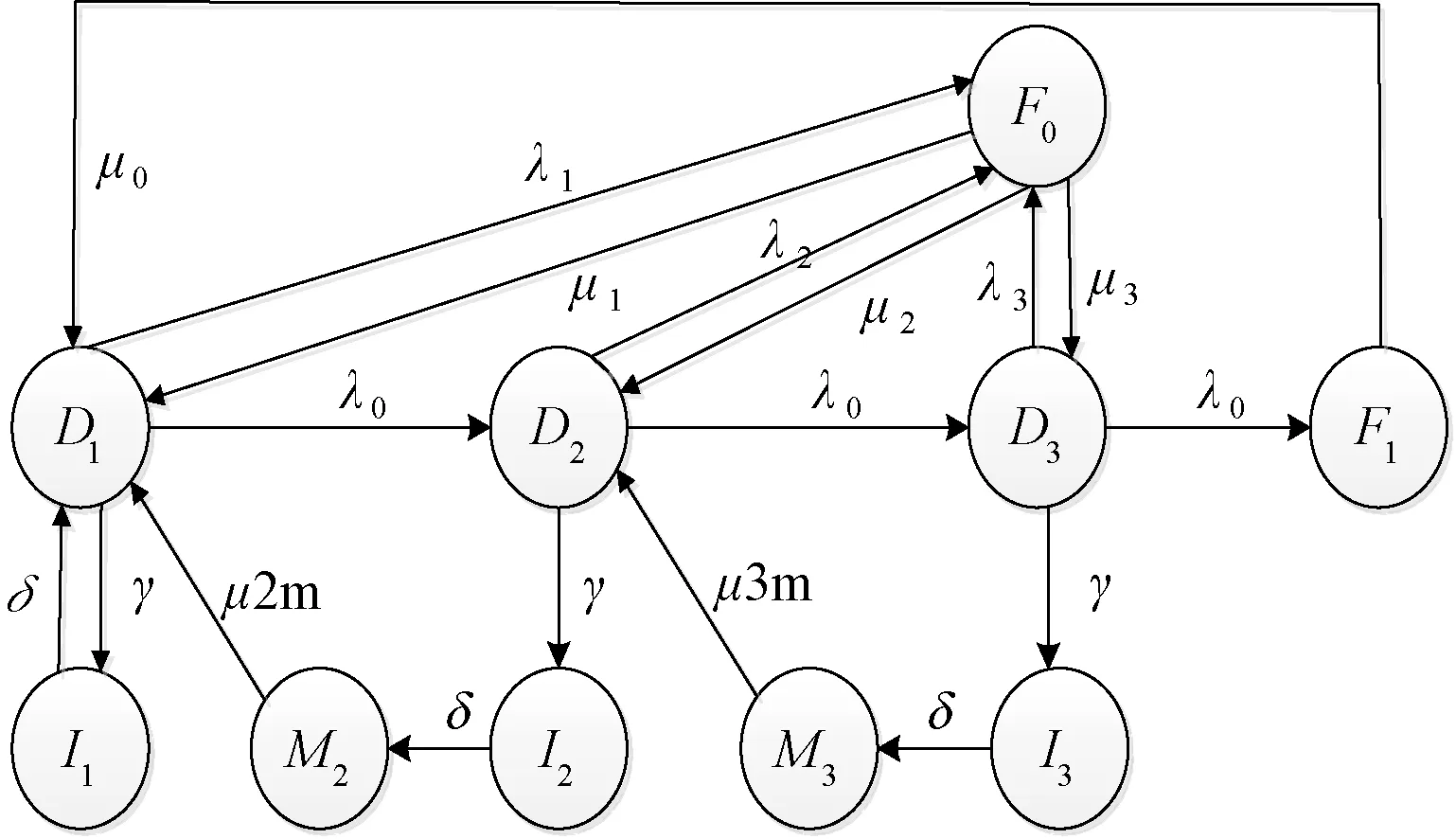
图4 发电系统老化和随机故障后的状态检修模型
根据发电系统的老化过程与实际检修情况分析,把发电系统分为3个老化阶段分别是D1、D2、D3,λ1、μ1、λ2、μ2、λ3、μ3分别表示系统处在各阶段内系统的失效率和修复率;状态F0、F1分别表示系统处在随机故障状态和老化故障状态,且假设各个老化阶段的时间服从均值1/λ0的指数分布,μ0是系统老化故障后的维修率;I1、I2、I3分别表示系统处在各老化状态时所对应的检测状态,1/γ为系统各状态的平均检测间隔时间,1/δ为各系统平均检测时间;M2、M3表示系统经过检测后进行的预防性维修状态,1/μ2m、1/μ3m分别表示系统处在D2、D3老化阶段内平均预防性维修时间。
在上述维修模型中,如果对系统不采取任何维修措施,系统将经过3个老化阶段最终进入老化故障状态F1,经过维修后系统可恢复到状态D1,除了D1状态不需要进行预防性维修外,其余老化状态下都需要采取预防性维修,系统可恢复至前一个状态,每次采取预防性维修前,要先对系统进行检测,确定系统状态和采取的检修动作;系统除了发生老化故障外,还会因偶发故障而进入随机故障状态F0,此时对设备进行故障后维修,系统可恢复至故障前的状态。
根据发电系统状态检修模型,运用马尔可夫过程原理,可得出发电系统检修模型的状态转移矩阵如下所示:
(14)
根据马尔可夫状态转移矩阵,得出发电系统状态的稳态方程组:
(15)
式中:P=[PD1PD2PD3PF1PF0PI1PI2PM2PI3PM3],P中的各元素分别表示为状态D1、D2、D3、F1、F0、I1、I2、M2、I3、M3的稳态概率。根据风力发电系统老化检修模型和状态转移概率矩阵,发电系统的正常运行的概率为:
(16)
4 实例计算及参数分析
目前,风电机组历史故障数据资料还比较少,这使得发电系统的可靠性参数很难获取,本文中发电机、变流器可靠性数据参考文献[8],而电刷滑环可靠性数据很少有文献提及,可参考某风场历史数据,风力发电系统各个部件的故障率和修复率,如表1所示。

表1 风机发电系统各部件3个老化阶段的可靠性数据
根据风场实际运营情况,发电系统的整体设计寿命为20年,采集风场发电系统的维护时间和维护次数,系统平均每次检测所需的时间为0.1天,第二劣化阶段的平均预防性维修需2天,第三劣化阶段的平均预防性维修需2.5天,系统老化故障后事后维修平均需要28天。
根据上表各部件的可靠性数据,计算得出发电系统可靠性数据,采用MATLAB编程软件进行数值计算分析,可得到该系统的检测平均间隔时间(1/γ)以及平均检测率(δ)对可用度的影响结果,分别如图所示。
由图5可以看出,系统的稳态可用度随检测平均间隔时间的增大而提高,当检测平均间隔时间为0.50年左右时,系统可用度缓慢上升逐渐趋于平稳状态,当检测平均间隔时间达到0.75年时,系统的可用度达到最大且为0.996 8。由图6看出,开始时系统的可用度随着检测时间的减少而增大,但当检测率达到20 000次时,即每次检测0.44 h左右时,系统的可用度趋于常数,检测可以发现设备的潜在故障,进行预防性维修,但检测本身不能使设备老化状态发生改变。
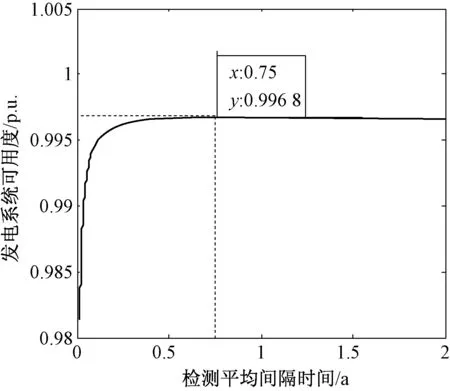
图5 检测平均间隔时间对系统可用度的影响
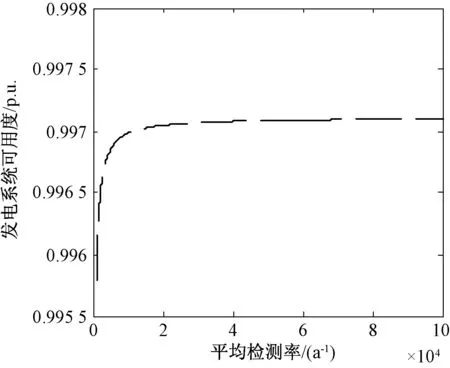
图6 平均检测率对系统可用度的影响
发电系统在实际运行中,由于运行环境的差异或不同类型风电机组材质的不同,机组的老化程度也会不同[16],因此,本文探究不同老化程度的发电系统检测平均间隔时间与系统稳态可用度的关系,如图7所示。
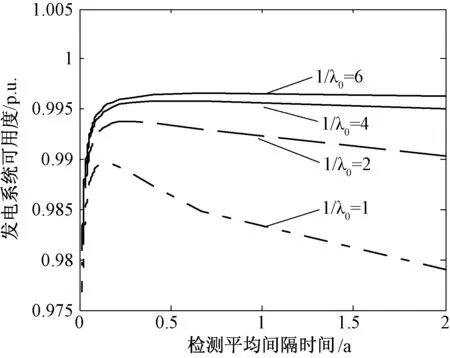
图7 不同老化系统检测平均间隔时间对可用度的影响
图7表明,发电系统的可用度与机组的老化程度有着重要的关系,老化间隔时间(1/λ0)越长,系统的稳定运行性能越好,系统的可用度也随着老化间隔时间的增大而提高。当系统老化间隔确定时,系统的可用度会随着机组的检测平均间隔时间先提高而后缓慢下降,因此检测平均间隔时间将会很大程度上影响系统的稳态可用度,不同老化系统存在最优的检测平均时间间隔,系统所对应的可靠度最优的检修策略如表2所示。
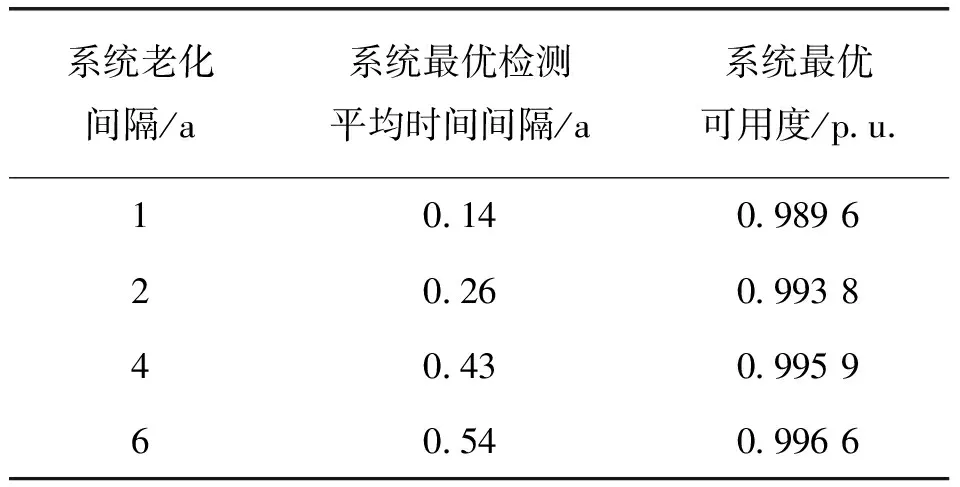
表2 可靠度最优时的检测策略
5 结论
本文在分析发电系统的运行原理和故障机制的基础上,建立了发电系统的可靠性数学模型,在考虑随机故障和老化故障的情况下,提出基于马尔可夫过程的改进型多状态维修模型,能有效地描述系统的性能退化过程并参考现有风场的可靠性数据,通过对检测平均间隔时间的优化,得出了不同老化间隔系统最优时的检修策略,为风电机组的检修工作人员进行优化检修提供了有力地理论支持。
风力发电机组是集机械、电气多部件的复杂系统,故障模式及运行状态复杂多样,运用马尔可夫过程简化了修复模型的分析,但是忽略了不同状态之间的持续时间,考虑系统多种状态模式,深入分析部件故障间的关系,建立涵盖多个风电机组的综合状态模型,实行联合检修的优化策略,还有待进一步研究。
[1]Tavner P J,Xiang J,Spinato F.Reliability analysis for wind turbines [J].Wind Energy,2007,10(1):1-18.
[2]彭华东,陈晓清,任明,等.风电机组故障智能诊断技术及系统研究[J].电网与清洁能源,2011,27(2):61-66.
[3]高扬,于会群,张浩,等.变速恒频双馈风力发电系统并网控制仿真[J].电力科学与工程,2014,30(2):1-6.
[4]李国栋,魏春,韩民晓.采用网侧TCVR的双馈风机低电压穿越控制策略研究[J].华北电力大学学报,2012,39(4):24-29.
[5]温子明.关于风力发电机组优化检修的探讨[J].电子世界,2012,(4):36-37.
[6]苏春,周小荃.基于半马尔科夫决策过程的风力机状态维修优化[J].机械工程学报,2012,48(2):44-49.
[7]Arabian H H, Oraee H,Tavner P J.Wind turbine productivity considering electrical subassembly reliability[J].Renewable Energy,2010,35(1):190-197.
[8]李大字,冯园园,刘展,等.风力发电机组可靠性建模与维修策略优化[J].电网技术,2011,35(9):122-127.
[9]Ribrant J, Bertling L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005[J]. IEEE Transactions on Energy Conversion,2007,22(1):167-173.
[10]Popa L M, Jensen B B,Ritchie E,et al.Condition Monitoring of Wind Generators [J].IEEE Industry Applications Society Annual Meeting,Salt Lake City, UT, USA, 12-16 October 2003:1839-1846.
[11]曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社,2012.
[12]李景禄,李青山.电力系统状态检修技术[M].北京:中国水利水电出版社,2011.
[13]Welte T M.Using state diagrams for modeling maintenance of deteriorating systems[J].IEEE Transactions on Power Systems,2009,24(1):58-66.
[14]汲国强,吴文传,张伯明,等.一种适用于状态检修的电力设备时变停运模型[J].中国电机工程学报,2013,33(25):139-146.
[15]姜学蕾.基于马尔可夫过程的电力设备检修优化决策[D].济南:山东大学,2013.
[16]Byon E,YU D.Season-dependent condition-based maintenance for a wind turbine using a partially observed Markov decision process[J]. IEEE Transactions on Power Systems,2010,25(4):1823-1834.
Reliability Modelling and Maintenance Strategy Optimization for Wind Power System
Qin Yang, Ma Huimin, Zhu Tianwei, Zhu Qinghua
(School of Electric Engineering, Shanghai Dianji University, Shanghai 200240, China)
Aiming at the problems related to reliability evaluation and operational maintenance for the wind power system, the operation principle and fault mechanism of the doubly-fed induction wind turbines were studied, and the reliability model of the double fed induction generation system was established using Markov process and reliability theory. Considering random failure and aging failure of the system an improved maintenance model for power generation system was proposed. The state transition matrix was obtained by using the relationship of the state transition, and the availability of system was solved by MATLAB software. The influence of detection time on system availability was also discussed. Finally maintenance srategies for different aging power generation systems with optimal reliability were obtained. The results indicate that the model can effectively evaluate the reliability of wind power system and provides theoretical support for the formulation of scientific maintenance schemes for wind turbines.
wind power system;markov process;reliability model;maintenance strategy;availability
2015-05-11。
上海市大学生创新活动计划项目(G2-13DXSCX-003)。
秦洋(1989-),男,硕士研究生,主要研究方向为风电机组的可靠性建模与维修策略的优化,E-mail:qinxueyang1989@163.com。
TM614
A
10.3969/j.issn.1672-0792.2015.07.010

