扩径导线的参数化有限元建模

万建成，董玉明，杨文刚，司佳钧，刘 龙，张秋桦

(1. 中国电力科学研究院，北京102200； 2. 华北电力大学 能源动力与机械工程学院，河北保定071003)

扩径导线的参数化有限元建模

万建成1，董玉明1，杨文刚2，司佳钧1，刘 龙1，张秋桦2

(1. 中国电力科学研究院，北京102200； 2. 华北电力大学 能源动力与机械工程学院，河北保定071003)

相比普通导线扩径导线更加经济、环保，采用有限元方法对扩径导线进行应力分析能够为其应用提供技术支持。针对扩径导线有限元建模问题，以JLXK/G1A-530(630)/45 3号扩径导线为例，研究扩径导线空间结构，确定股线的接触位置，并进行了参数化的有限元建模。结果表明：提出的有限元建模方法通过接触位置确定，可减小接触的面积，从而可减少接触非线性计算的时间；采用参数化建模可研究不同结构参数的扩径导线，减少建模工作量。

扩径导线；有限元模型；接触；参数化

0 引言

架空输电导线是输电线路的重要组成部分，是空中能源输送通道的主干道。在工程实际状态下，受自身结构及自然环境的影响，架空线力学特性复杂[1，2]，对其进行力学特性的研究具有重要的工程应用意义。

扩径导线属于架空线的一种，由于其环保及经济的特点，得到了广泛的应用[3]。研究扩径导线的力学特性除了实验的方法[4]外，常用的方法为有限元数值仿真方法[5～7]。

有限元仿真常规的建模方法是通过三维软件如CAD或Pro/E建立其几何模型，然后导入到有限元软件如ANSYS里面。该建模方法工作量大，效率低，且模型导入过程容易出现问题，不利于有限元仿真工作的进行。

为了提高建模效率，避免大量常规工作的重复进行，本文采用参数化的方法完成扩径导线的建模，不仅可提高工作效率，同时，方便不同结构参数的扩径导线的研究。

1 扩径导线空间结构推导

扩径导线空间结构复杂，为建立正确合理的数值模型，就需要研究扩径导线内股线的具体分布、相邻绞层股线接触的具体位置。

1.1 扩径导线截面内股线截面分布

以绞线层内任意股线为例，在一个节距内，该股线的轴线为螺旋曲线。沿股线的轴线截取一微元段，其轴线可视为直线，即为直圆柱，如下图1所示。

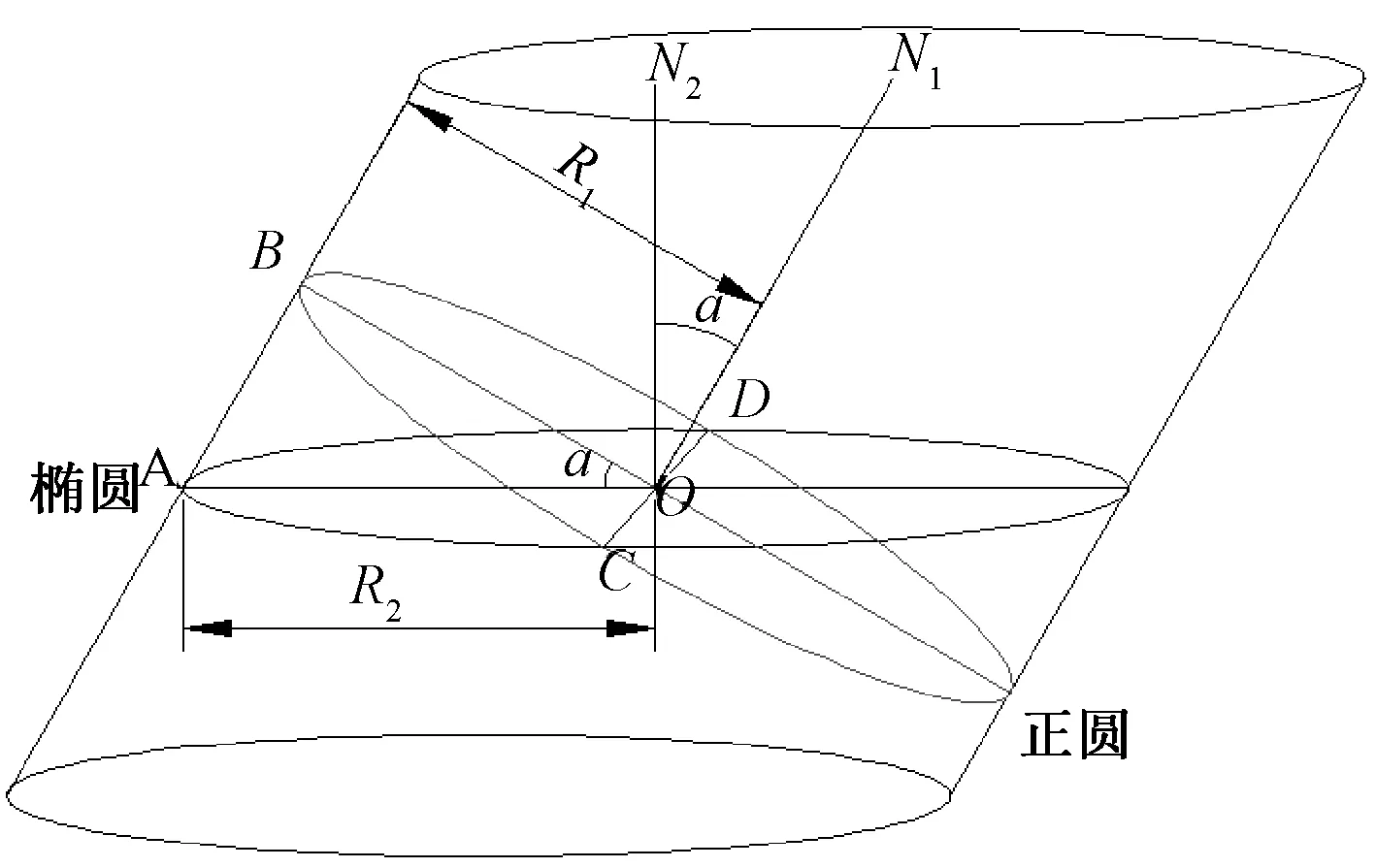
图1 螺旋股线微元段

图1中微直圆柱中间的椭圆面是绞线横截面上该股线的截面形状。该椭圆长半轴为OA=R2，ON2为过该椭圆面中心的一条法线。过椭圆中心作该微直圆柱的横截面，易知横截面为圆面，该圆面与面AON2的交线为OB=R1(即股线的半径)，与椭圆面的交线为CD=2R1，为圆面的直径。在椭圆面AOC上，椭圆上的点距中心O最长距离为长半轴OA，又因为椭圆上的点位于直圆柱面上，直圆柱面上的点到点O的最短距离为直圆柱的半径，而OC=OD=R1，说明CD为椭圆面的短轴，既CD⊥OA。过圆心O作圆面的法线ON1，而该法线正好是股线螺旋轴线在点O的切线，所以∠N1ON2是该层股线的螺旋角，故∠N1ON2=α由几何关系可知∠AOB=∠N1ON2=α，故

(1)

由面AON1⊥AOC知，股线螺旋轴线在点O处的切线ON1在椭圆截面上的投影方向即为其椭圆截面的长轴。

图2(a)所示为导线中心钢股和相邻绞层线股的横截面示意图。其中O1为中心钢股的圆心，O为相邻绞层某股的圆心。以O1为圆心的小圆是钢股的横截面，以O为圆心的椭圆是相邻绞层某股的横截面。以O1为圆心的的大圆是外绞层股线轴线在绞线截面上的投影，O1O为大圆的半径，故切线ON1⊥O1O，因而在绞线截面上，外绞层椭圆截面的长轴与中心股线横截面的某条直径垂直，且该直径与椭圆截面的短轴共线。在图2的坐标系下，长轴所在的直线方程为

(2)

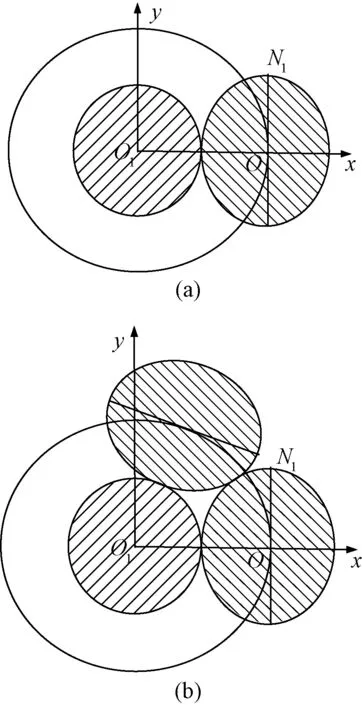
图2 螺旋股线局部截面

从以上分析可知，外绞层股线椭圆截面的短轴与中心股线截面的某条直径重合，长轴方向则为螺旋轴线的切线在该横截面上的投影方向，如图2(b)所示。

1.2 接触位置的确定

在扩径导线的精细化有限元分析中，需要考虑扩径导线的接触非线性问题，为建模方便需要确定其接触位置。扩径导线内的接触分为三种[5]：中心股线与螺旋钢股线间的线接触、相临绞层间股与股间的点接触、同绞层内股线间线接触。由于在扩径导线内，同绞层内的线接触影响相对较小[8]，故仅考虑前两种。故本文中接触位置的推导也就分为两类，线接触与点接触。

1.2.1 线接触

线接触分布于中心股线与螺旋钢股线间，根据图2(b)中的坐标系，中心股线与螺旋钢股线的接触位置位于两截面中心O,O1的连线上，即两根股线的接触位置参数方程为

(3)

式中：R1为中心股线半径；β为指螺旋股线在坐标系内的分布角；m为该位置距绞线起始平面的距离；L2为指螺旋股线的节距。

1.2.2 点接触

扩径导线螺旋钢股线与中心钢股线的接触属于线接触，而相临绞线层由于旋向相反，铝绞线层与钢绞线层或铝绞层间的接触为点接触。绞线横截面局部示意图，如图3所示。

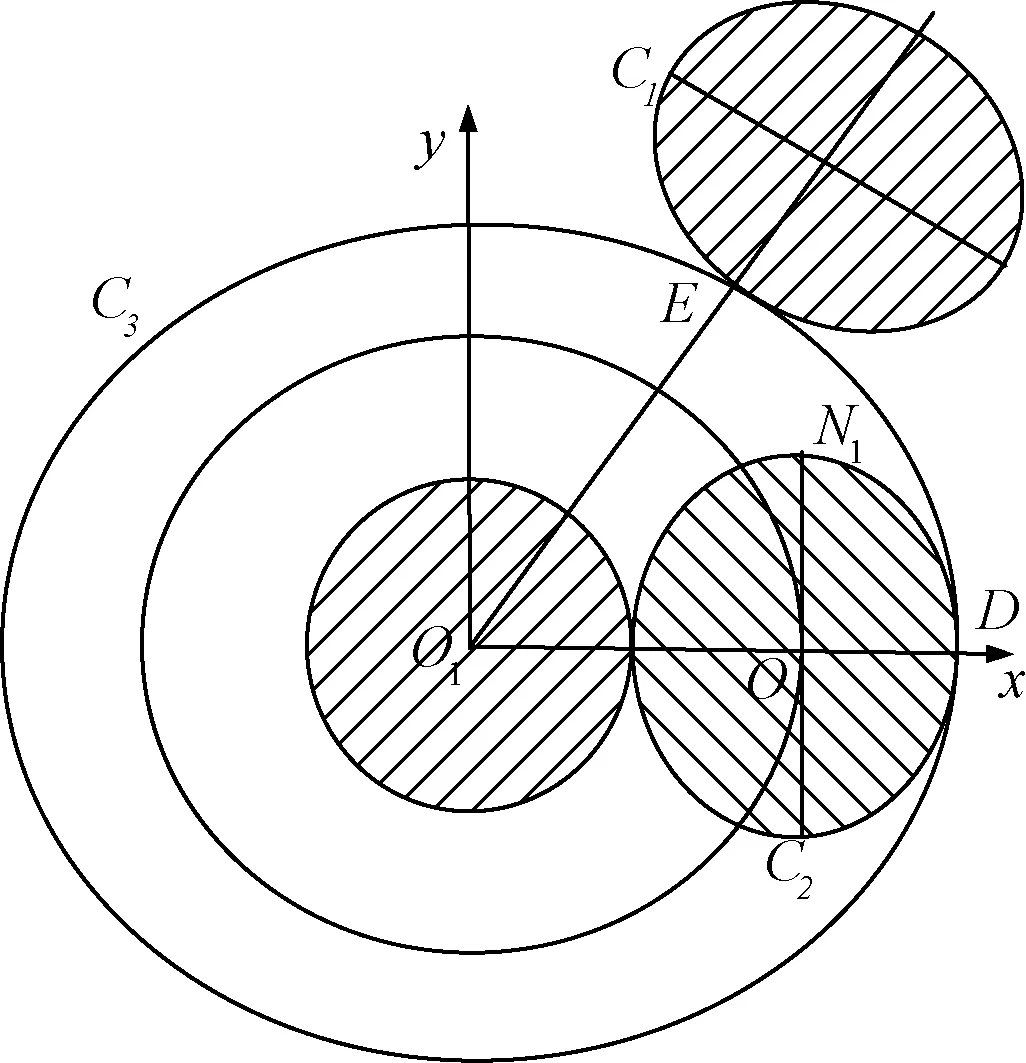
图3 股线间点接触局部图示

如图3，内绞线层内某股线截面椭圆曲线C1与圆截面曲线C3相切于点E，由螺旋钢股线层内股线与中心钢股线接触可知，内绞线层层内股线与圆截面曲线C3所在直圆柱面接触为一条螺旋曲线，平面z=m上的接触点E即位于该曲线上，此曲线的方程为

(4)

同理可得，点D的参数方程为

(5)

式中：β与β′符号相反；L3为内绞层的节距。连立式(4)(5)可得内绞层与螺旋钢绞层点接触距绞线起始面距离为

(6)

把式(6)代入式(4)或(5)便可得内绞层与螺旋钢绞层股线接触位置。式(6)求导过程具有普适性，故也可由其求得其它相临绞层间接触点的位置。

通过以上推导表明，绞线沿其垂直轴线的截面内，螺旋股线截面的短轴方向与中心股线截面的某条直径方向重合，长轴方向则为螺旋轴线的切线在该截面上的投影方向。扩径导线空间结构的推导，为其参数化实施提供了理论依据。

2 扩径导线参数化建模

本文以JLXK/G1A-530(630)/45 3号扩径导线为例，对其进行参数化建模。该型号扩径导线具体结构为中心为7根钢股线，外面为三层铝绞层，最外层内股线紧密排列，中间两层内股线不相临均匀排列。其具体结构参数如表1。

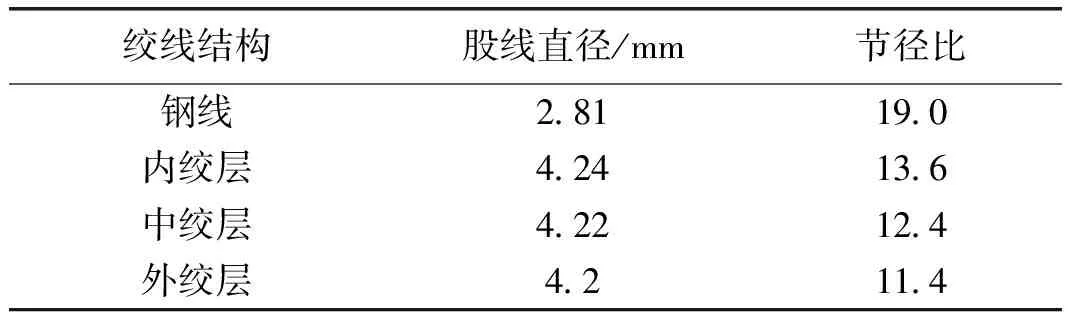
表1 扩径导线结构参数

2.1 有限元模型

基于扩径导线空间结构对其进行参数化建模，其难点是接触的设置，为降低利用模型加载计算时的计算成本，参数化建模过程，对接触位置处进行了特殊处理。

2.1.1 材料定义

扩径导线参数化建模中，材料模型采用双线性等向强化模型，钢股线及铝股线弹性模量分别为E=206 GPa与E=60 GPa，泊松比均为μ=0.3，屈服极限分别为σ=1 100 MPa与σ=170 MPa，图4为钢及铝的简化本构关系曲线。

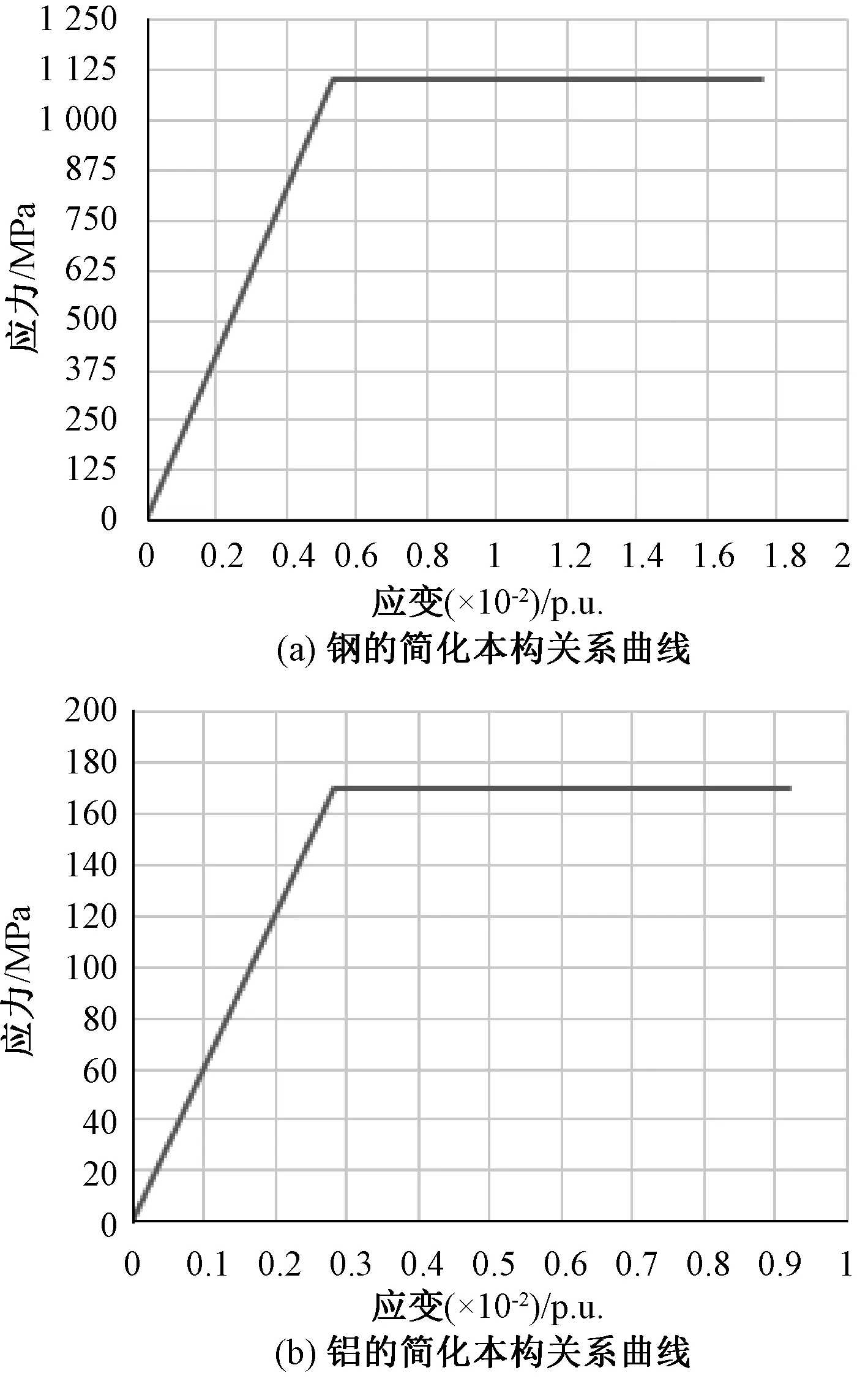
图4 钢及铝的简化本构关系曲线

2.1.2 单元的选取及接触设置

本文采用实体单元模拟扩径导线，考虑到在外载荷作用下股线间的接触、弹塑性变形等问题，计算模型具有强非线性，因此选用8节点的Solid185非线性单元。在计算过程中需要考虑股线间的接触问题，由于建模采用三维实体模型，这里选用接触的目标单元为TARGE170，接触单元为CONTA174通过面接触的形式来模拟股线间的接触形为[9～12]。

2.2 建模

为减少建模时间，便于调整模型参数，利用ANSYS提供的二次开发工具APDL实现扩径导线的参数化建模，提高扩径导线研究分析的效率及模型的重复可利用性。

扩径导线参数化建模流程如图5所示。首先建立各绞层一根股线的截面，并根据扩径导线的空间结构及接触位置的确定，把单根股线截面分为接触体与非接触体截面，如图6(a)所示；对接触体的截面通过平移旋转生成中心股线局部接触体，如图6(b)所示；复制中心股线局部接触体旋转生成某层股线的接触体如图6(c)所示；按照上述方法，依次生成各层接触体如图6(d)所示；建立非接触体，最终扩径导线的几何模型如图6(e)所示；按照2.1节所述的方法，指定材料属性，通过选择接触体指定接触对，并进行网格划分，建立的有限元模型如图6(f)所示。

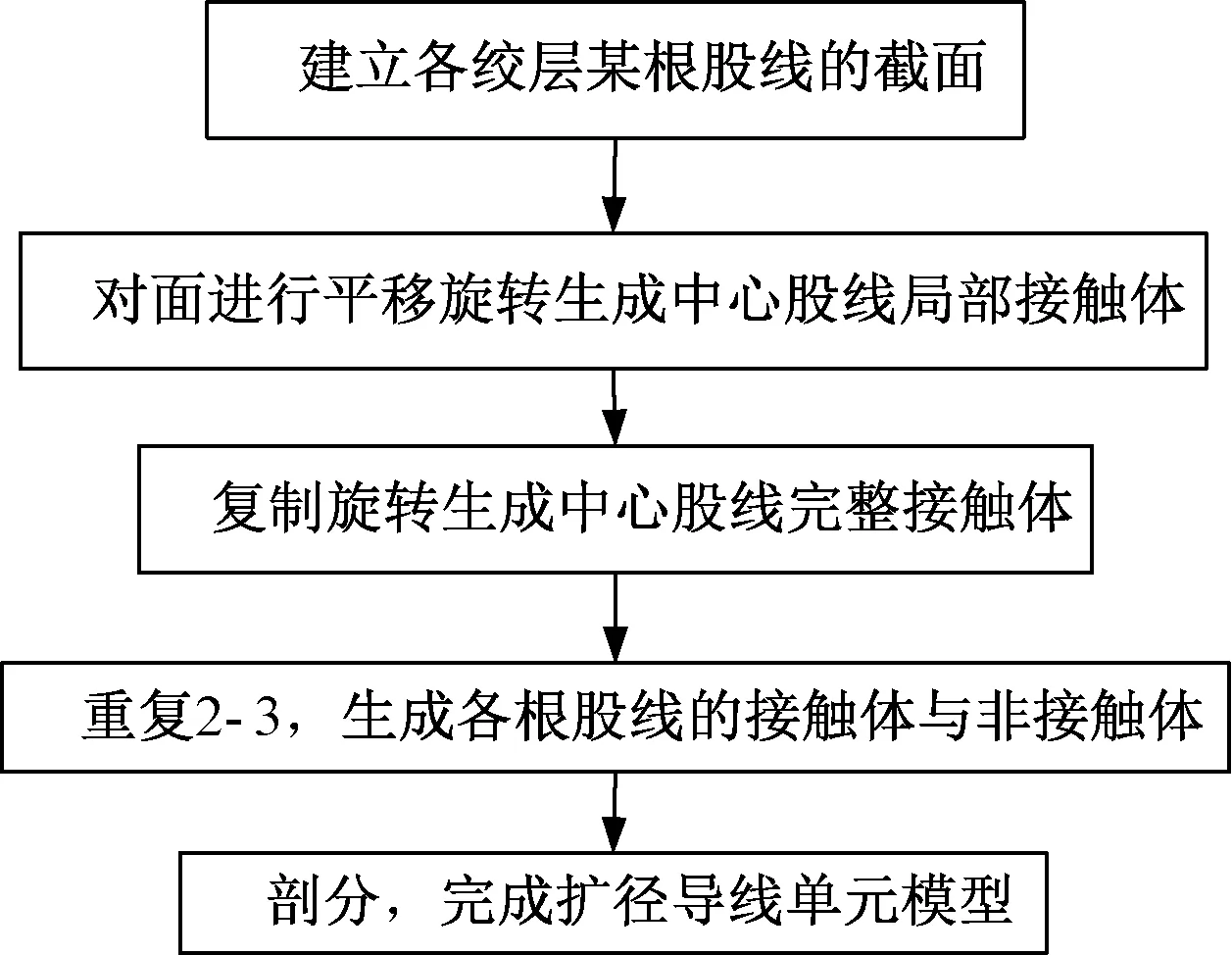
图5 参数化建模流程图

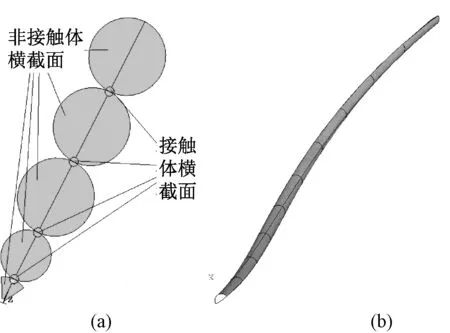
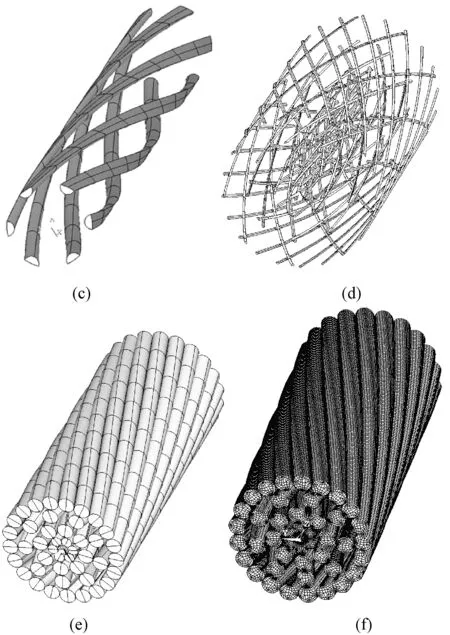
图6 扩径导线建模过程

3 结论

本文针对扩径导线在传统建模过程中存在的问题，对扩径导线的参数化建模方法进行了研究。实现了JLXK/G1A-530(630)/45 3号扩径导线的参数化建模，可缩短扩径导线仿真分析时间，通过参数的调节，即可研究不同结构参数的扩径导线，避免大量工作的重复操作，减少了建模工作量。

[1]孟遂民，孔伟．架空输电线路设计[M].北京：中国电力出版社，2007．

[2]王桂兰，孙建芳，孙海鸥．钢丝绳捻制成形的空间几何模型与有限元分析[J]．应用力学学报，2003，20(3)：82-86．

[3]张禄琦，郝阳，李小亭，等. 扩径导线在特高压交流输电线路工程中的应用[J]. 电力建设, 2012, 33(8):92-95.

[4]万建成，刘臻，孙宝东，等. 扩径导线的分类与扩径方式的选择[J].电力建设, 2010,31(6): 113- 118.

[5]万建成，司佳钧，刘彬，等. 一种结构稳定的大截面扩径导线设计[J]. 电力建设,2013, 34(10):92-96.

[6]赵新泽，周权，高伟．钢芯铝绞线同层线股间接触有限元分析[J]. 三峡大学学报(自然科学版),2011,33(1):69-72.

[7]卢青针，肖能，阎军，钢管脐带缆弯曲刚度有限元分析[J]. 计算机辅助工程,2011,20(2):16-19，38.

[8]Jolicoeur C, Cardou A. Semicontinuous Mathematical Model for Bending of Multilayered Wire Strands [J]. J. Eng. Mech.,1996, 122(7):643-650.

[9]赵万友. 接触问题的分析方法研究与工程应用[D]. 西安:西安电子科技大学, 2007.

[10]李妍. 基于ANSYS软件的接触问题分析及在工程中的应用[D].长春：吉林大学, 2004.

[11]梁春. 基于三维真实粗糙表面的弹塑性接触有限元分析[D]. 镇江：江苏大学, 2009.

[12]张红军. 基于ANSYS的汽车轮胎有限元分析研究[D]. 西安：西安理工大学, 2005.

The Parameterized FEM Model for Expanded Conductor

Wan Jiancheng1，Dong Yuming1, Yang Wengang2，Si Jiajun1, Liulong1, Zhang Qiuhua2

(1. China Electric Power Research Institute, Beijing 102200, China; 2. School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

Compared with ordinary conductor, the expanded conductor is more economic and environmentally friendly. The finite element method can provide technical support for the stress analysis of the expanded conductor. To solve the problem of the finite element modelling of the expanded conductor, this essay took JLXK/G1A-530(630)45 3 expanded conductor as an example, and confirmed the contact position between strands based on the study of the space structure of the expanded conductor. Then parameteric finite element modelling was carried out. The result shows that the time spent on contact nonlinear calculation can be reduced with the confirmation of the contact position between strands, which can reduce the area of contact. Accordingly, the parametric modeling can help to study expanded conductor with different structural parameters and reduce the workload of modelling.

expanded conductor; FEM; contact; parameterization

2015-03-30。

国家电网公司科技项目(GCB17201400076)。

万建成(1971-)，女，高级工程师，从事导地线和金具研究、设计，E-mail:wanjiancheng@epri.sgcc.com.cn。

TM73

A

10.3969/j.issn.1672-0792.2015.07.014