一种新的基于多频谱叠加的图像配准算法

张轶飞，牛守瑞，马 娜，张长泉



一种新的基于多频谱叠加的图像配准算法

张轶飞1，牛守瑞1，马 娜2，张长泉1

（1. 63963部队 北京 100072；2. 中科院高能物理研究所 北京 100049）

针对现有频域法FFT和PPFFT对于大倍率图像配准精度和计算效率难以同时保证的问题，研究了一种基于多重频谱叠加的频域算法，为最大限度减小插值误差噪声，该算法采用多分辨率频谱插值，构造出更接近对数极坐标网格。文中给出分辨率参数设置和算法流程。最后通过算例验证，结果表明：本算法对无裁减图像最大配准倍率可至10，对裁减图像可至5，而FFT和PPFFT（无迭代）对于两种类型图像都约为2；相对于特征点匹配法，本算法也适用于更大倍率的图像配准，从而验证了该算法的准确性和可行性。

多重频谱；大倍率配准；对数极坐标；插值误差

0 引言

图像配准是图像运动估计的关键，广泛应用于图像嵌入、视频压缩、电子稳像及图像增强等领域[1-5]。一般地，配准方法主要分为空域法和频域法两种。频域法主要有傅里叶变换法（FFT）[6-7]、伪极数傅里叶变换法（Pseudo Polar FFT，PPFFT）[8-10]等。空域法主要有块匹配法[11]、灰度投影法[12]及特征匹配法等[13]。相较于空域法，频域法抗噪性强、不受亮度变化影响，且计算简单，易于实现。在传统的FFT法和PPFFT法实现过程中，坐标变换易产生较大的插值误差，使配准精度降低。FFT法最高配准倍率较低，最高为2[7]，而PPFTT法最高配准倍率虽可达4[9]，但需经过多次迭代，计算效率则较低。显然传统方法在配准倍率和计算效率上难以兼备。

本文基于图像的多分辨率频谱叠加，提出一种改进方法，该方法无需迭代，且能实现大倍率图像的配准。

1 图像配准信噪比及噪声种类

1.1 配准信噪比

一般地，图像信噪比（Signal Noise Ratio, SNR）是针对单幅图像质量而言，表达为图像信号与噪声的功率谱之比，又可近似等于峰值信噪比10×lg(2552/MSE)。但在基于频域法的图像配准中，两种图像能否准确配准，则取决于其互功率谱的傅里叶反变换图像的最大值位置是否准确。文献[9]给出了配准信噪比的定义：

并证明该式满足：

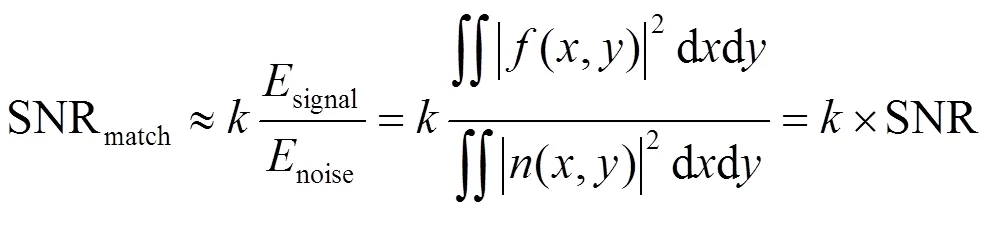
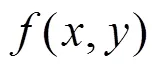
显然，正常情况下，配准信噪比最大值处对应正确的配准参数。但当噪声强于信号时，则会产生误匹配，因此区分噪声种类，并予以去除或减弱，尤为重要。

1.2 噪声种类

式(2)表明，SNR越大，配准信噪比越高。而SNR又与噪声功率成反比，因此，最大限度降低图像经缩放、旋转及配准过程中插值等产生的频谱噪声，能提高图像配准精度。

一般，图像噪声可分为以下3种。

1）旋转混叠

图像经旋转后，其离散傅里叶变换将产生多处叠加现象。这是因为图像不是无限周期延伸的，尤其当图像采样频率小于2倍频谱截止频率时。该噪声主要表现为频谱的高频部分，文献[14]提出采用窗口函数来消除该噪声，但同时也会削弱真实信号能量。

2）倍率混叠

当图像被放大某一倍率时，其频谱也被相应放大，单周期内的频谱高频部分与相邻周期的频谱可能产生重叠，从而产生倍率混叠噪声。通常这种噪声可通过低通滤波减弱，但对于大倍率图像，因滤波带宽难以估计，滤波函数往往会淹没真正的图像信息。

3）插值误差

插值误差是指图像频谱从笛卡尔坐标或伪极坐标变换至对数极坐标时，因插值计算产生的误差噪声。

上述误差中，旋转和混叠噪声，随角度和缩放倍率变化，难以通过固定窗口的加窗函数和固定带宽的滤波函数进行消除，而插值误差噪声，则可通过改进插值方法予以降低。

以下将重点围绕如何降低插值噪声，研究对数极坐标下非均匀网格的特点，设计多分辨率傅里叶变换的分段插值，来提高配准精度。

2 改进方法

改进方法按多频谱网格的构建、多重参数设置及改进算法流程逐一介绍。

2.1 多分辨率频谱构建

1）对数极坐标网格特点

频域法进行图像配准时，是对两幅图对数极坐标下的幅度谱进行比较。图1示出极坐标和对数极坐标网格。显然，极坐标网格沿径向均匀分布，而对数极坐标网格则是沿径向由密至疏非均匀分布。将图1横纵坐标替换为径长和角度，则如图2所示。图2更直观显示出纵坐标方向网格的非均匀分布情况。传统的FFT和PPFFT法，都是基于均匀网格，而后插值出对数极坐标网格。从图2看出，在径长较大处时，由于均匀网格间隔与对数极坐标网格相当或更小，插值误差将较小，而在径长较小处时，均匀网格则明显大于对数极坐标网格间隔，此时，插值结果将会产生较大误差，影响匹配结果。

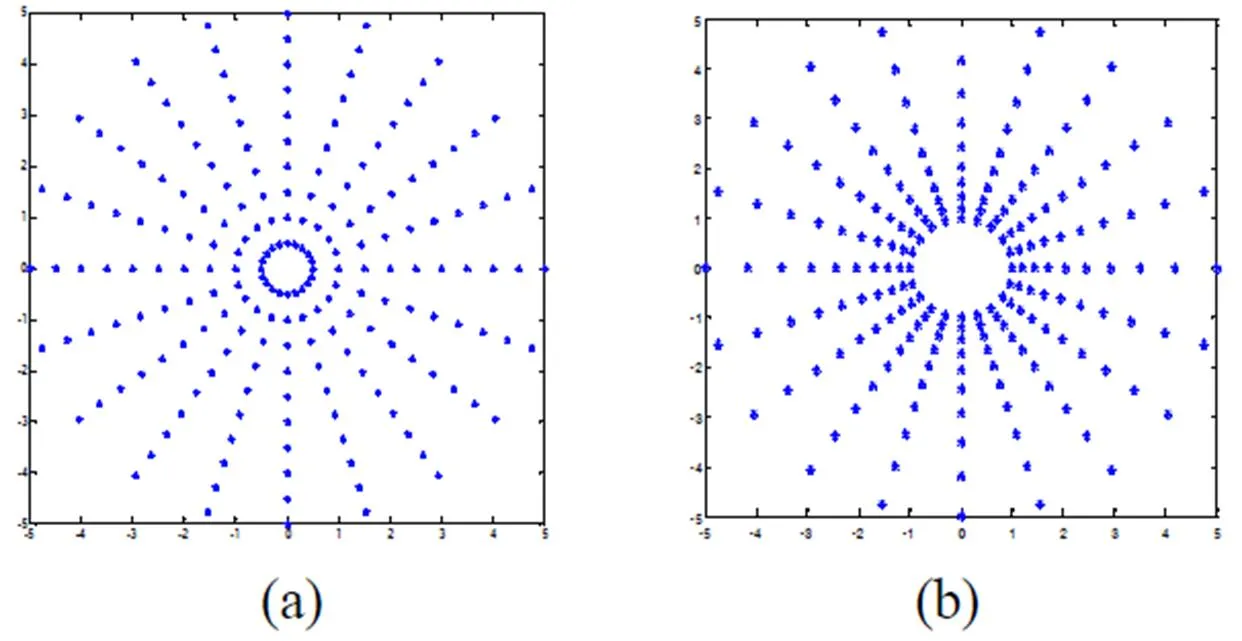
图1 笛卡尔坐标下均匀极坐标网格和对数极坐标网格比较

图2 均匀极坐标网格和对数极坐标网格比较

2）构建过程

根据以上分析，考虑构造一种类似图2(b)的网格，使其更接近对数极坐标网格。

离散傅里叶变换（DFT）有如下表达形式：

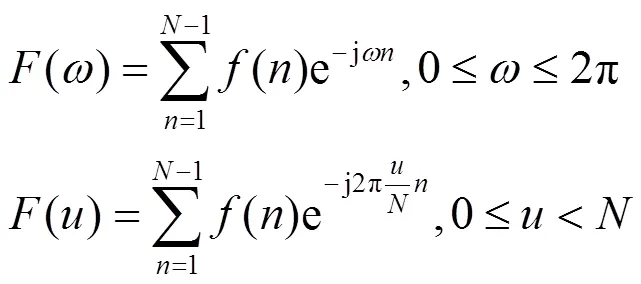
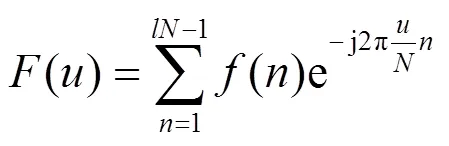
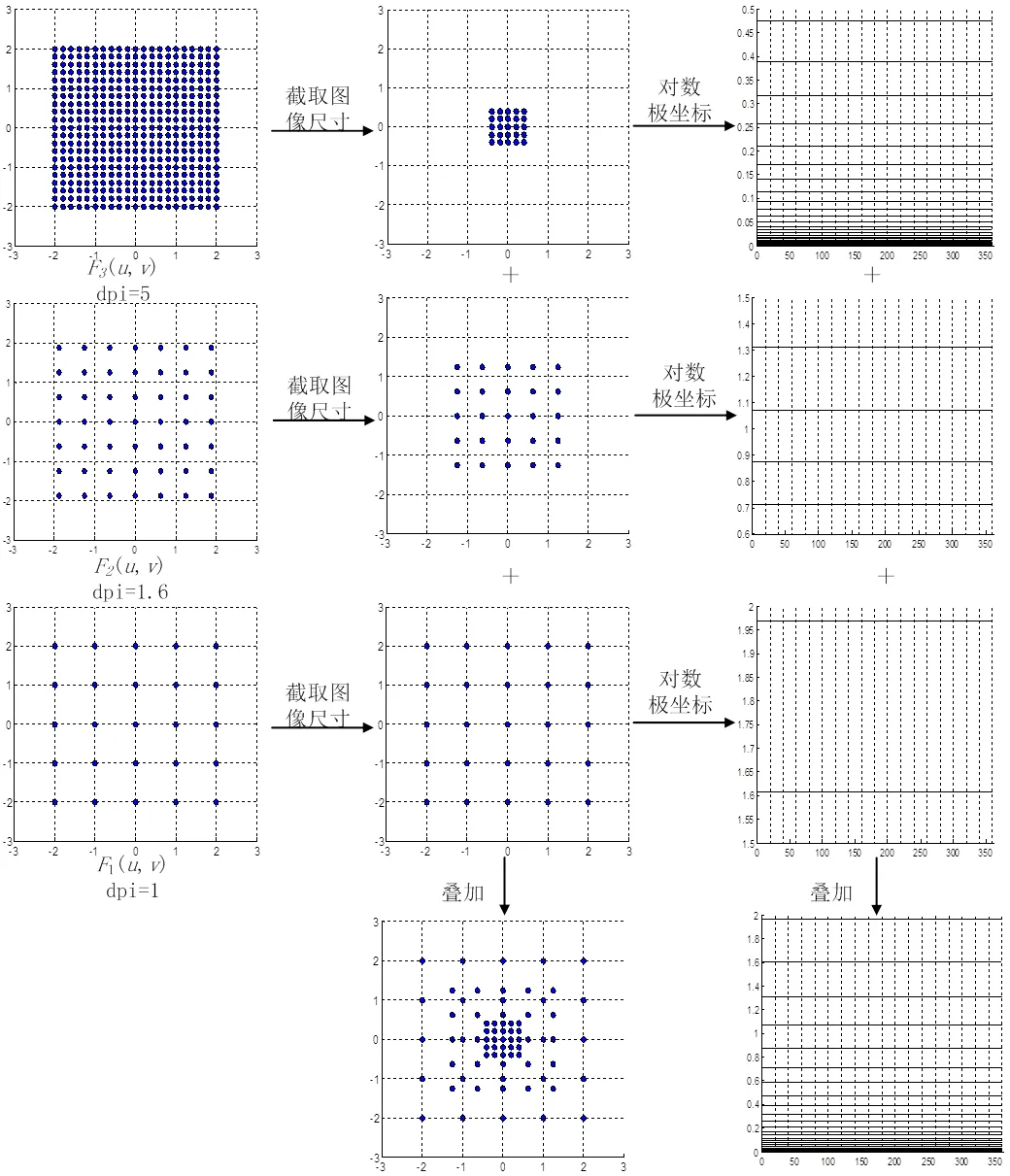
图3 多分辨率网格叠加示意图

另外式(4)还可以通过分数傅里叶变换得到：

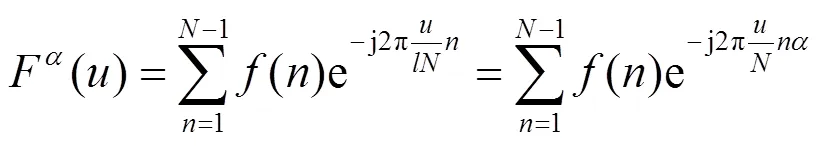
0≤＜，＝1/

考虑到频谱集需要叠加，为便于对中，将频域变量范围定义为关于原点对称，则有－p≤≤p，于是式(4)变为：

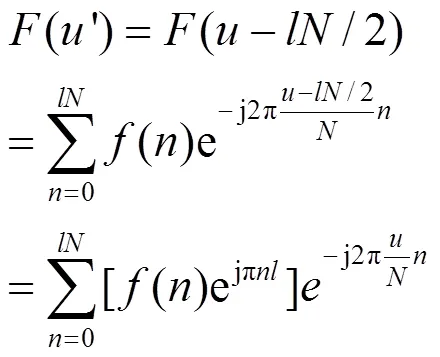
0≤＜，－(/2)≤¢＜/2

同样，将式(5)对中，可变为：

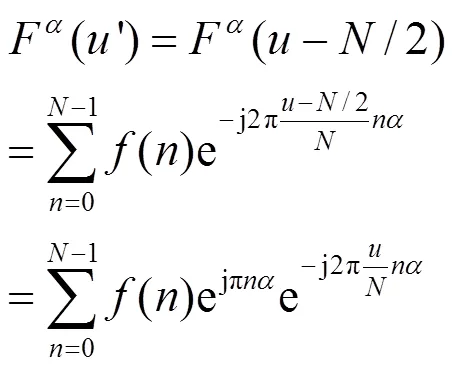
0≤＜，－(/2)≤¢＜/2，＝1/

比较式(6)和(7)可知，二者得到的频谱范围－p≤≤p和－p≤≤p，即前者得到的频谱矩阵规模更大，而后者仅与原频谱相当。事实上，当进行多分辨率频谱叠加时，若将由式(6)得到的各频谱矩阵全部叠加，其本质相当于取最大分辨率值（即为最大）的频谱，且计算量极大，失去了叠加的意义。因此应对式(6)得到的全频域频谱进行截取，得到与原图像尺寸相当规模的频谱矩阵。而式(7)无需截取可即得到所需规模的矩阵。从计算量来看，式(6)的运算量为10×()，而式(7)则只需30×()，因此，用分数傅里叶变换更快捷。

2.2 多重频谱参数设置

如上所述，通过设置多重频谱并叠加，能使叠加后的频谱更接近实际频谱。其中，各频谱的分辨率（即细化参数）的选取设置是关键。在确定参数设置之前，先分析一下频谱插值误差及网格插值误差。

1）一阶频谱插值误差函数

对于某频谱为的图像，定义一阶插值误差[9]为：

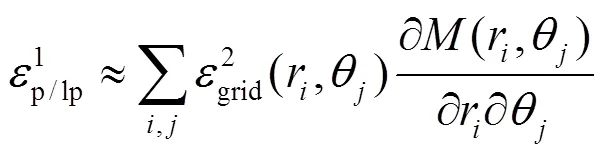
式中：grid(r,)为实际频域点与网格中最近点距离，表示为：

2grid(r,)＝(closet－real)2＋(closet－real)2(9)

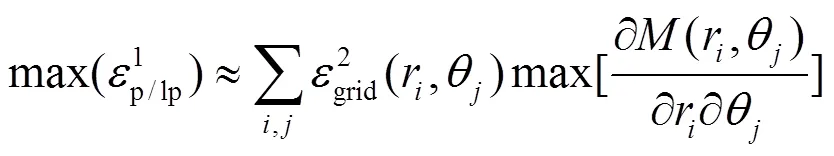
2）频谱参数计算

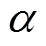
建立200×200的二重均匀网格和对数极坐标网格，并计算error。误差曲线和误差曲面如图4、图5所示。

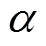
表1反映出，传统的笛卡尔及伪极坐标网格都为均匀网格，与极坐标网格插值比较看，伪极坐标明显优于笛卡尔坐标网，同时也优于多重频谱网，但与对极数坐标网的插值误差则明显增大，而多重网格叠加的优势则比较明显，随着网格层数的增加，其插值误差明显减小，当达到五重网格叠加时，插值误差可达到传统笛卡尔及伪极坐标网的1/3和1/2左右。从多重网格参数比较看，优化后的参数较随机选取的参数能得到更小的插值误差。同时，注意到多重网格同一参数下p较lp更大，这时因为对数极坐标网大部分点聚集在内层高分辨网格，插值误差更低，而极坐标网格外层低分辨网格内插值点较多，因此，各点插值误差求和后，仍可能使二者相差相大。综合来看，可以得到如下结论：多重网格叠加能明显改善插值精度，当网格层数超过2时，与对数极坐标网格插值误差大大低于伪极坐标网格；多重网格插值精度随网格层数增加而增高；多重网格采用优化参数较非优化参数具有更高的精度。

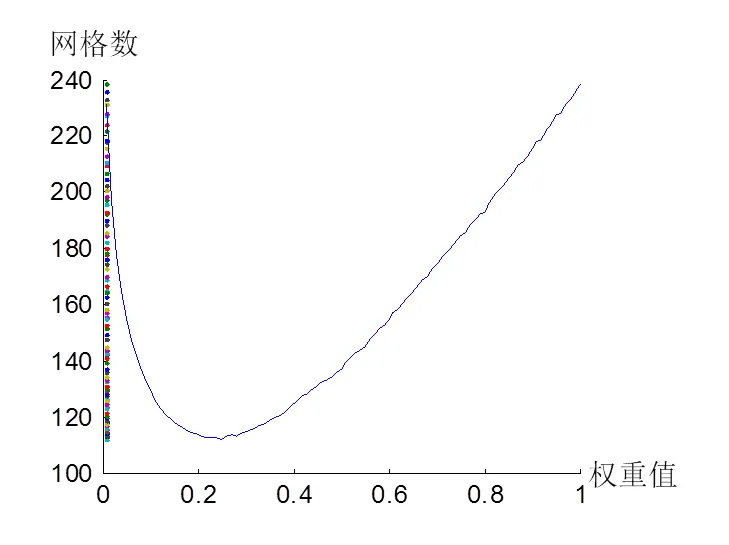
图4 二重频谱参数曲线

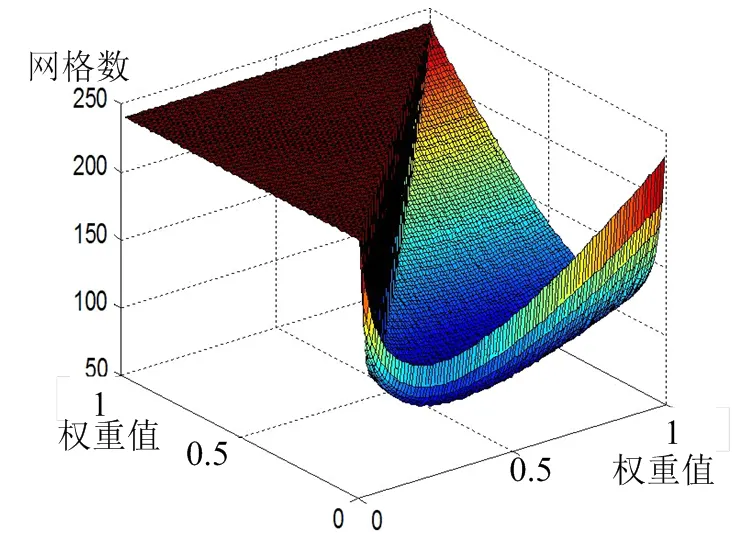
图5 三重频谱参数曲面

表1 各类网格插值误差比较

2.3 改进算法流程步骤

综上所述，采用多重网格能明显改善与对数极坐标网格的插值精度，因此，基于傅里叶变换，采用多重频谱叠加，可以得到改进算法。具体实现步骤如图6所示。

图6 改进算法流程图

Fig 6. Improvedalgorithm flow chart

3 实验分析

3.1 单一图像不同倍率下配准比较

采用改进方法与FFT、PPFFT法进行图像配准，分别测试同一图像不同放大倍率下的配准情况，如图7所示，所用图像均未经裁剪。实验平台为CPU intelE31230双核3.2G，内存4G的PC机，编程软件为Matlab，测试图像分辨率均为256×256。

图7 各倍率配准图

从表2结果看，前3组放大倍率在5以上的图像样本，FFT和PPFFT法均无法配准，而改进法则能准确匹配。而放大倍率为2的图像样本，用3种方法均可正常匹配，这与文献[7]、[9]阐述一致。由此可见，改进法对于无裁剪图像可配准恢复的最大倍率约为10，且无需迭代，计算效率更高。同时改时法叠加层数在3～4层时，精度变化已经很小。通常采用改进法层数设置为3～4即可。

图像经放大后，在相同分辨率下，超出部分会被裁剪，这就造成图片信息的丢失。换言之，同一幅图片，在经过放大剪切处理后，其有效频域范围变窄，干扰频率增加，增大了配准难度。

3.2 各类图像配准效果比较

分别选用不同类型图片进行配准比较。实验选用图片来自加州大学USC图像库，从中选出如图8所示的具有代表性图片，上述图片中包含了头像、建筑、风景、重复纹理、航拍全景等风格。配准分裁剪和未裁剪两种情形。裁剪情形，设定放大倍率为5，旋转角为20°；未裁剪情形，设定放大倍率为10，旋转角为20°。分别采用FFT、PPFFT、改进法及特征点匹配法进行比较。其中，为保证较高精度，改进法设置为4层，特征点匹配法采用鲁棒性和精度较好的SURF算法[13]。

表2 各图配准结果

表3显示出，对于放大倍率为5，有裁剪图像样本，改进法能准确配准；FFT和PPFFT均不能正确匹配；SURF法仅对4幅图能准确匹配，成功率较低。表4显示出，对于倍率为0.1，无裁剪情形，改进法能准确匹配；其他方法均无法正确匹配。另外，通过对USC图像库中样本大量计算表明，改进法的图像配准倍率范围约为0.1～5。

3.3 图像拼接

通过配准后，将图像拼接，进一步验证改进算法的有效性。图9(b)和图9(c)分别为图9(a)局部的不同倍率、角度、平移后的图像。分别采用改进法、PPFFT法和SURF法进行配准比较。

改进法配准后拼接效果如图9(d)所示，各算法计算结果比较如表5所示。

图8 图像样本集合

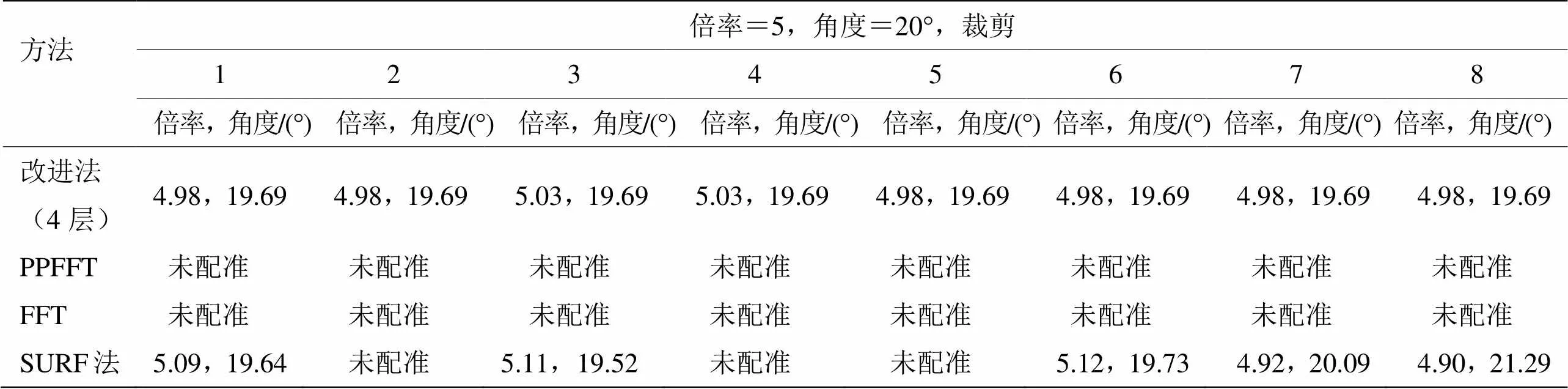
表3 裁剪后各图不同方法下配准结果比较

表4 未裁剪各图不同方法下配准结果比较

图9 配准拼接图

表5 改进法与PPFFT、USRF法配准参数比较

图9(d)显示出改进法对各图配准后，均能恢复到原图中正确的位置，图中在配准位置存在部分细长的白色边缘线，说明配准后的(,)坐标参数存在较小的误差。表5反映出改进法对图9中两个局部放大图均能正确计算其参数，PPFFT法是均计算错误，无法配准。SURF法对于较小放大倍率局部图9(b)可实现配准，但对倍率5.2的图9(c)无法实现配准。可见，改进法在大倍率图像配准中优于PPFFT法和传统的特征点匹配法。

4 结论

频域法是图像配准的重要方法，因其抗噪性强、不受图像亮度变化影响、计算简单而应用广泛。针对现有频域法FFT和PPFFT对于大倍率图像配准精度和效率难以同时保证的问题，本文研究了一种基于多重频谱叠加的频域算法，立足于最大限度减小插值误差噪声，该算法通过多分辨率频谱插值构造更接近对数极坐标网格，并给出了分辨率参数设置和算法流程。最后通过实验进行验证，结果表明：改进法对无裁减图像最大配准倍率可至10，对裁减图像可至5，而FFT和PPFFT（无迭代）对于两种类型图像都约为2；相对于特征点匹配法，改进法也适用于更大倍率的图像配准。

[1] 王磊, 葛镜, 熊曼子. 帧间预测编码中的运动估计算法研究[J]. 计算机与数字工程, 2007, 35(12): 28-31.

[2] 钟锦, 吴昊. 雾天视频图像增强与运动目标跟踪模型及方法[J]. 计算机仿真, 2013, 30(8): 402-407.

[3] 徐端全, 朱光喜. 基于帧间预测的视频水印算法[J]. 计算机工程与应用, 2008, 44(24): 22-24.

[4] 陈钱. 红外图像处理技术现状及发展趋势[J]. 红外技术, 2013, 35(6): 311-318.

[5] 杜小平, 刘明, 夏鲁瑞, 等. 基于光谱角累加的高光谱图像异常检测算法[J]. 中国光学, 2013, 6(3): 325-331.

[6] 周武, 胡跃明. 基于相位相关和重采样的亚像素图像配准算法[J]. 华南理工大学学报, 2010, 38(10): 68-73.

[7] Reddy B S, Chatterji B N. An FFT-based technique for translations, rotations and scale-invariant image registration[J].. 1996, 5(8): 1266-1271.

[8] 刘汉洲, 郭宝龙, 冯宗哲. 基于傅里叶变换的遥感图像配准[J]. 光电子×激光, 2006, 17(11): 1393-1397.

[9] Keller Y, Averbuch A, Israeli M. Pseudopolar-based estimation of large translations, rotations and scalings in images[J]., 2005, 14(1): 12-22.

[10] Liu H, Guo B, Feng Z. Pseudo-Log-Polar Fourier Transform for Image Registraion[J]., 2006, 13(1): 17-20.

[11] 赵振民, 彭国华, 符立梅. 基于形状模板的快速高精度可靠图像匹配[J]. 计算机应用, 2010, 30(2): 441-444.

[12] 吴浩, 邓宏彬, 何少阳. 基于分块灰度投影的无人飞行器视频稳像方法[J]. 北京理工大学学报, 2013, 33(4): 385-389.

[13] 刘少鹏, 郎跃东, 丁祝顺. 改进的SURF算法及其在目标跟踪中的应用[J]. 传感器与微系统, 2012, 31(12):148-152.

[14] Harold S Stone, Bo Tao, Morgan. Analysis of image registration noise due to rotationally dependent alising. Commum[J].2003, 14(2):114-135.

A New Image Registration Method Based on Overlaying of Multiple Spectrums

ZHANG Yi-fei1，NIU Shou-Rui1，MA Na2，ZHANG Chang-quan1

(1. 63963,100072,; 2.,100049,)

Of frequency-domain method, registration accuracy and efficiency of FFT or PPFFT for large scale image is difficult to be obtained simultaneously. With this problem considered, a new registration method based on overlaying of multiple spectrums is proposed, which interpolates spectrums of multi resolution and generates the grid closest to log-polar, to minimize interpolation error noise. In addition, how to set resolution parameter and the algorithm flow is also explained. Finally, to validate the accuracy and feasibility of the algorithm, three examples were calculated through the new algorithm, and the result shows as followed: as for the image without cutting, the maximum registration scale of the improved method without iterations can reach 10, and as for the image with cutting, the same one can reach 5, while the FFT and PPFFT (non iterative) for the two kinds of image is about 2; compared with the feature point matching method, the improved method is also applied to image with larger scale.

multiple spectrum，large scale registration，log-polar ordinary，interpolation error

TP391.41

A

1001-8891(2015)05-0424-07

2014-11-02；

2015-01-18.

张轶飞（1980-），男，工程师，博士，主要研究图像匹配、电子稳像等。E-mail：flightzyf@126.com。

中国博士后科学基金，编号：2012T50870。