基于ST与量子理论模型的红外与可见光图像融合
张耀军,吴桂玲,栗 磊
基于ST与量子理论模型的红外与可见光图像融合
张耀军,吴桂玲,栗 磊
(信阳农林学院计算机系,河南 信阳 464000)
针对传统的红外与可见光图像融合方法计算复杂度高、运行机制过于机械的问题,提出一种基于剪切波变换(ST)与量子理论(QT)模型的红外与可见光图像融合方法。该方法利用ST优越的图像信息捕捉性能对源图像进行多尺度多方向分解;其次,采用QT理论针对低频子带图像和一系列高频子带图像进行融合;最后,采取ST反变换获得最终融合结果图像。
剪切波变换;量子理论;图像融合;红外图像;可见光图像
0 引言
来自红外传感器的红外图像侧重于探测和描述场景中相关目标的热辐射信息,能够在光线条件不佳的情况下显示暴露在场景中或遮蔽物后的热源目标;而可见光图像是利用场景中目标的光反射信息对图像加以显示,侧重于整体场景环境信息的描述,因此,可见光图像信息的多寡很大程度上取决于场景中的光线水平。不难看出,红外图像与可见光图像之间存在大量的互补信息,将二者信息加以融合并归入一幅图像中无疑将大幅提升图像的信息量。目前,红外与可见光图像的融合已经成为信息融合领域内的热点问题,相关研究成果也被广泛应用于反恐等军事领域[1-4]。
目前,红外与可见光图像的融合主要采用变换域方法加以进行。小波变换被用于完成两类图像的融合,并取得了良好的实验效果[5-10]。由于经典小波变换仅能捕捉奇异“点”信息而不能捕捉奇异“线”信息,基于此,脊波变换[11]、曲波变换[12-13]以及轮廓波变换[14-15]等变换域图像融合方法相继出现,较大幅度地提升了图像融合性能。剪切波变换(shearlet transform,ST)[16-18]相比前几类模型,无论在图像信息捕捉能力还是算法计算复杂度方面均占有显著的优势,并已经逐渐成为图像融合领域内的主流方法和热点研究对象,目前,ST已被广泛地应用于图像融合、图像特征提取等领域。
另一方面,Tseng等人在2003年提出将量子理论(quantum theory,QT)模型[19]用于图像处理领域,实验结果表明QT模型能够从纯数学的角度利用计算机的比特特性对图像融合问题加以研究,极大程度地避免了以往融合规则制定过程中主观因素的干扰。Mao等人[20]将QT模型用于图像去噪,取得了良好的图像处理效果。
本文针对传统的红外与可见光图像融合方法计算复杂度高、运行机制过于机械的问题,提出一种基于ST与QT模型的红外与可见光图像融合方法。首先,将利用ST对源图像进行多尺度、多方向的分解,各生成一幅低频微观子带图像和一系列高频微观子带图像。然后,采用QT模型完成对应微观子带图像的融合过程。最后,采用ST反变换生成最终融合结果图像。
1 ST基本模型
Easley等在文献[21]中构造了合成膨胀下的仿射系统模型,并提出在维数=2条件下的系统表达公式:

式中:Î2(2);和为可逆矩阵,矩阵规模为2×2,且满足|det|=1。若M()满足紧支撑条件,则M()的元素为合成小波。称为各向异性膨胀矩阵,与尺度变换相关联;为剪切矩阵,与保持面积不变的几何变换相关联。和的表达式分别为=[0, 01/2],=[1, 0 1]。简单方便起见,通常取=4,=1,即=[4 0, 0 2],=[1 1, 0 1]。此时,该合成小波即为剪切波。
令2(2)满足下列条件:
*()=*(1,2)1*(1)2*(1/2) (2)
*表示函数的傅氏变换,1和2分别满足:


每一个剪切波位于近似大小为22j×2、线方向斜率为2-j的梯形对上,如图1(a)所示。根据小波理论,由一维小波张成的二维小波基具有正方形的支撑区间,在尺度,其近似边长为2,如图1(b)所示。当尺度变大时,小波支撑基的面积随之变大,但是由于其无方向性,非零的小波系数以指数形式增长,导致大量不可忽略的系数出现。小波逼近奇异曲线最终表现为“点”逼近过程,而非原曲线最优的稀疏表示。剪切波以近似长条形即梯形对去逼近曲线,当尺度变大时,其支撑基的线方向斜率2-j也随之变化,使得这种近似长条形的支撑基具有各向异性,能够有效捕获方向信息,它是图像中边缘等特征的真正的稀疏表示。图2给出了剪切波变换中的频率分割示意图。

图1 ST与二维离散小波支撑区间示意图

图2 ST频率分割示意图
2 QT模型
Tseng等[19,22-23]提出:不同于经典比特的含义,量子比特是一种包含有两种完全相反基态的量子系统,每一个量子比特可以表示为这两种基态的线性组合,即:
=*|0>+*|1> (5)
式中:表示一个量子比特系统,|0>与|1>分别代表两种基态,、分别为两种基态的系数,需要注意的是,、均为复数,且满足下式:
||2+||2=1 (6)
因而,结合式(5)、(6)可知,在一个量子比特系统中,基态|0>出现的概率为||2,而基态|0>出现的概率为||2。
对应至一幅已经经过归一化处理后的灰度图像,(,)表示其中的像素点灰度值,由于(,)的数值介于0和1之间,因此,可以用量子比特系统来表示图像,其中灰度值为1的概率系数为(,),灰度值为0的概率系数为1-(,),即满足下式:

式中:两种基态|0>和|1>分别表示像素点灰度值为0时以及像素点灰度值为1时的状态。
进一步地,对单个像素点信息进行扩展,延伸至邻域像素点灰度值信息,以行相邻像素点(-1,),(,),(+1,)为例,由于每个像素点均存在0和1两种初始基态,因此,3个像素点共可以构成8种基态:000,001,010,011,100,101,110,111。故量子比特系统可以表示为:

沿用量子坍缩理论,仅针对中心像素点(,)进行处理,则式(8)可以改写为(9)、(10)。
显然,量子坍缩理论消除了原先行邻域中中心像素点灰度值对整个邻域造成的潜在影响,这一思路与现行许多基于区域像素点的图像处理方法是相吻合的。
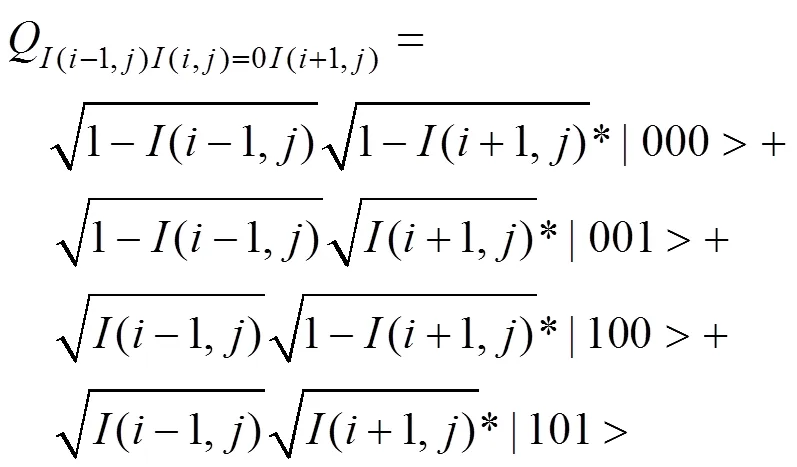

3 基于ST与QT模型的红外与可见光图像融合算法
基于上节中的QT模型和量子坍缩理论,可以得出例如在(i-1, j)=1,(,)=1,(+1,)=1状态下的概率。结合式(8)、(10),可以得到像素点(,)的重构灰度值:
(,)=|111>/|111> (11)
式中:|111>=(-1,)(,)(+1,)|111>,b|111>=(-1,)(+1,)|111>。
假设归一化后源图像的数量为,ST将对幅源图像进行分解,并得到一系列低频微观子图像和高频微观子图像。针对K幅图像中的同一空间位置像素点1(,),2(,),…,I(,),其初始基态概率为1|111>,2|111>,…,a|111>,坍缩后的基态概率为1|111>,2|111>,…,b|111>,则幅源图像的最终融合图像F为:

提取各项的概率密度,式(12)进一步改写为:
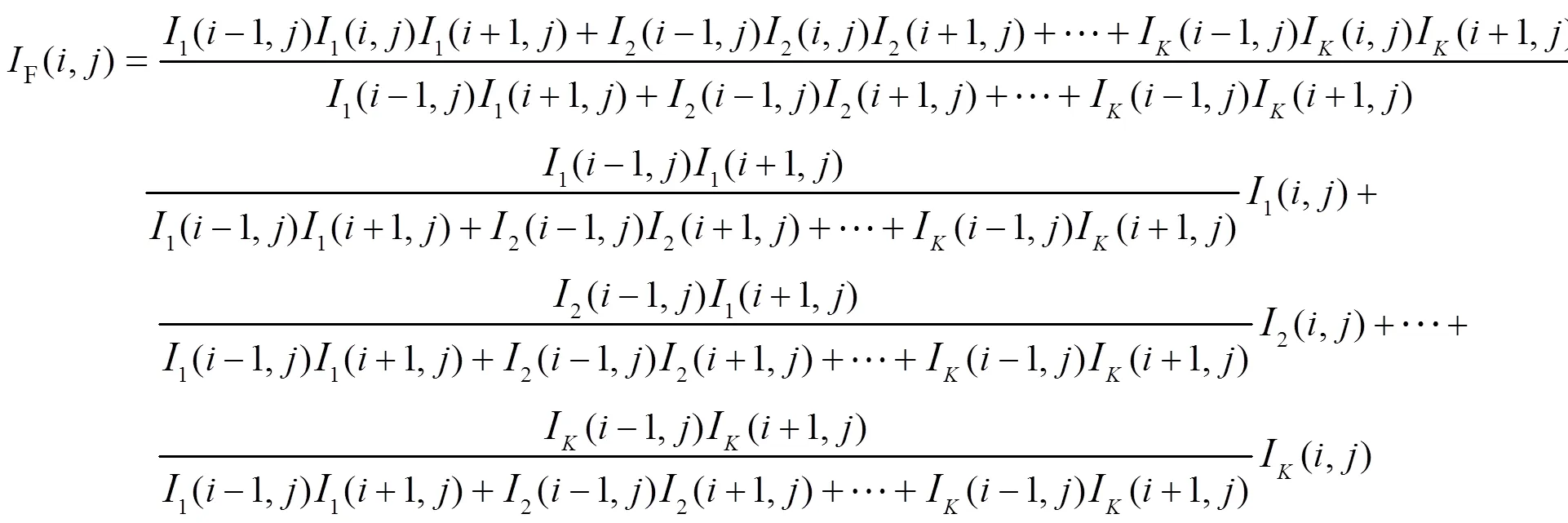
简单起见,令式(13)中的各项系数为1,2,…,a,显然1+2+…+a=1。因此,式(13)等价于对幅源图像像素点灰度值的加权处理。特别地,当系数的分母为0时,可以选取灰度值最大的像素点作为最终融合图像中的像素点。
图3给出了以两幅源图像为例的基于ST与QT模型的红外与可见光图像融合过程。

图3 基于ST与QT模型的红外与可见光图像融合过程
首先,采用ST理论获得一系列多尺度、多方向下的微观子图像;接着,利用构建的QT模型实现对应尺度、对应方向的微观子图像的融合过程;最后,进行ST反变换获得最终结果。这里,以两幅待融合红外与可见光源图像A和B为例,其中A和B为关于同一场景的不同图像传感器获取的已完成配准的源图像。其中,A、B为两幅源图像,low和high分别代表低频微观融合子图像和高频微观融合子图像部分,ST表示剪切波变换,F表示最终融合图像。基于ST与QT模型的红外与可见光图像融合算法具体步骤如下:
INPUT:两幅已配准的红外与可见光源图像A和B;
OUTPUT:最终融合图像F;
STEPS:
1)ST将源图像A、B分解为低频微观系数{A, 0,B, 0}和高频微观系数{A, L,B, L},其中,尺度级数为,是下的方向分解级数;
2)分别计算低频微观系数和高频微观系数的概率密度数值,完成高、低频微观子图像的融合过程。
3)利用ST反变换对融合后的低频微观子带融合图像和一系列高频微观子带融合图像进行处理获取结果图像F。
4 仿真实验
为了验证本文方法的实际运行效果,本节选取两组已配准红外与可见光图像作为待融合源图像进行本文方法的性能验证实验,并以WINDOWS 7系统和MATLAB 2012为平台,仿真、比较与分析包括本文方法在内的几种融合方法的融合效果。
两组待融合源图像如图4所示。其中,这两组图像均含有256级灰度级,且图片大小均为512×512像素。在第一组待融合源图像中,可见光图像仅能捕捉到场景中的背景信息,譬如镭射光下的商铺名称,但由于光线条件较差,其他信息没有能够得到很好地体现和描述;在红外图像中,我们可以发现该场景中实际上包含了大量的信息,如街道左侧的行人以及行驶中的两辆汽车等。在第二组待融合源图像中,光线条件较好,背景信息量大且纹理较为清晰,但无法捕捉到隐藏在丛林中的热源信息;而红外图像中可以准确地捕捉到热辐射源信息,发现丛林中的人员信息。显然,将同一场景中的红外与可见光图像加以融合将极大地丰富原始待融合源图像中的重要目标信息。

图4 仿真源图像
在融合仿真实验中,本文方法的参数设置情况如下:ST多尺度分解级数为3层,按照尺度分解次序,各尺度下的方向分解级数分别为10,10和18,邻域空间半径=3。为了与本文方法作比较,本节还选取了另外3种方法,分别为:多通道PCNN方法(方法1)[24]、ST方法(方法2)[18]以及拉普拉斯变换方法(方法3)[25]。为了保证融合效果的公正客观性,方法1~方法3中的参数仍沿用相关文献中的设置模式。融合结果除采取主观评价外,还选取了信息熵(IE)[26]、互信息量(MI)[26]以及空间频率(SF)[26]3种客观评价指标作为评价依据。IE数值表征图像中包含信息量的大小,数值越大,融合图像信息越丰富。MI数值反映了最终融合图像与源图像间的交互信息,MI数值越大,表征融合图像中涉及到源图像的原始信息越丰富。SF可以在一定程度上反映融合图像中各像素点的活跃程度,SF数值越大,代表融合图像包含的显著信息越丰富。IE,MI,SF的详细内容请参见文献[26]。图5,图6给出了两组待融合源图像的融合效果图。

图5 第一组待融合源图像融合效果图

图6 第二组待融合源图像融合效果图
实验结果表明,基于方法1的融合图像在主观视觉效果上非常糟糕,在实验一中出现了大量的虚假信息,在实验二中的视觉效果非常模糊,待融合源图像中的信息并没有在最终融合结果中得以体现。基于方法2生成的最终融合效果图像虽然较方法1有所改观,但在细节信息表达上表现不佳,例如商铺篷布上方的“NERO”标记非常模糊,难以识别,实验二中也损失了部分源图像中的栏杆信息。方法3相对于方法1、方法2而言有较好的视觉效果,实验一中的汽车以及“NERO”标记已经可以辨别出来,在实验二中也对待融合源图像中的主体和细节信息进行了较好地融合和表达,但有关人体的红外信息不太完整。相比前3种方法,基于本文方法的融合效果图像更为清晰,拥有更理想的主观视觉效果,表现也更令人满意。
表1中列出了两组融合实验中以IE、MI、SF为客观评价指标的评价结果。表格内容显示:结果表明,方法1的融合结果在IE、SF两项指标上较方法2、3有明显优势,从侧面表明方法1的融合图像含有较丰富的信息和较高的活跃程度。本文方法较其他3种融合方法拥有更理想的客观指标结果,无论在信息量、交互信息量还是空间频率指标上均占有显著优势。显然,客观评价结果与主观视觉评价效果是基本一致的。
以上两组仿真实验分别从主观视觉效果和客观评价指标两个方面验证了本文方法的合理有效性。此外,计算代价也是衡量算法性能的重要指标之一。为了尽可能保证比较的客观公正性,本节选取第二组仿真实验为例,对每种方法均运行3次给出算法的平均运行时间,如表2所示。黑色粗体代表本方法3次实验中的最佳数据。
由表2数据可知,方法1由于运行机制不涉及多尺度几何变换,因此在平均运行时间指标上占有明显的优势,仅耗时1.362s;方法3的融合机制较为复杂,因此较其他3种方法较为耗时;方法2和本文方法均涉及ST变换,但本文方法采用量子理论模型对微观子带图像进行融合,因此具有更低的计算复杂度。综合表1和表2数据分析,本文方法不仅具有更理想的图像融合效果,而且在算法运行效率上同样占有较为明显的优势,预期能够适用于实时性要求较高的应用领域。

表1 四种融合方法的客观指标值比较

表2 算法平均运行时间比较
5 结论
本文综合shearlet变换理论以及量子理论模型的优势,提出一种新型的红外与可见光图像融合方法。本文首先对待融合源图像进行多尺度、多方向分解,接着采用量子理论模型作为高、低频微观子带图像的融合方法。仿真实验选取了两组源图像进行实验,实验结果表明本文方法无论在直观视觉效果还是客观评价结果中均占有显著的优势。
[1] Li X, Qin S Y. Efficient fusion for infrared and visible images based on compressive sensing principle[J]., 2011, 5(2): 141-147.
[2] Chang X, Jiao L C, Liu F, et al. Multicontourlet-based adaptive fusion of infrared and visible remote sensing images[J]., 2010, 7(3): 549-553.
[3] Kong W W, Lei Y, Ni X L. Fusion techniques for grey-scale visible lightand infrared images based on non-subsampled contourlet transform and intensity hue saturation transform[J]., 2009, 5(1): 75-80.
[4] Ulusoy I, Yuruk H. New method for the fusion of complementary information from infrared and visual images for object detection[J]., 2011, 5(1): 36-48.
[5] 郑继明, 耿金玲. 小波变换在图像融合中的应用研究[J]. 重庆邮电大学学报: 自然科学版, 2008, 20(5): 561-567.
[6] 刘斌, 刘维杰, 彭嘉雄. 采用三通道不可分对称小波的红外与可见光图像融合[J]. 红外与激光工程, 2011, 40(5): 974-979.
[7] 孙新德, 刘国梅, 薄树奎. 基于QPSO和统计特征的红外与可见光图像融合[J]. 红外技术, 2014, 36(11): 900-904.
[8] 刘思汝, 杨风暴, 陈磊. 基于关键帧提取的红外与可见光序列图像快速融合[J]. 红外技术, 2014, 36(5): 350-354.
[9] 王宇庆, 王索建. 红外与可见光融合图像的质量评价[J]. 中国光学, 2014, 7(3): 396-401.
[10] 陈小林, 王延杰. 非下采样变换的红外与可见光图像融合[J]. 中国光学, 2011, 4(5): 489-496.
[11] 赵子沂, 郑永果. 基于脊波的多光谱和全色图像融合方法研究[J]. 计算机工程与应用, 2012, 48(15): 164-167.
[12] 赵景朝, 曲仕茹. 基于Curvelet变换与自适应PCNN的红外与可见光图像融合[J]. 西北工业大学学报, 2011, 29(6): 849-853.
[13] 薛琴, 范勇, 李绘卓, 等. 基于曲波变换的红外与可见光图像融合算法[J]. 计算机工程, 2011, 37(3): 224-226.
[14] 王斐, 梁晓庚, 崔彦凯, 等. 非负矩阵分解和新轮廓波变换的图像融合方法[J]. 计算机工程与应用, 2013, 49(5): 150-153.
[15] 莫建文, 马爱红, 首照宇, 等. 基于Brenner函数与新轮廓波变换的多聚焦融合算法[J]. 计算机应用, 2012, 32(12): 3353-3356.
[16] 冯鑫, 王晓明, 党建武, 等. 基于Shearlet变换的红外与可见光图像融合[J]. 光电子×激光, 2013, 24(2): 384-390.
[17] 郑红, 郑晨, 闫秀生, 等. 基于剪切波变换的可见光与红外图像融合算法[J]. 仪器仪表学报, 2012, 33(7): 1613-1619.
[18] Miao Q G, Shi C, Xu P F, et al. A novel algorithm of image fusion using shearlets[J]., 2011, 284(6): 1540-1547.
[19] Tseng C C, Hwang T M. Quantum digital image processing algorithms[C]//16th,, Kinmen, 2003: 827-834.
[20] Yuan S Z, Mao X, Chen L J, et al. Quantum digital image processing algorithms based on quantum measurement[J]., 2013, 124(23): 6386-6390.
[21] Easley G, Labate D, Lim W Q. Sparse directional image representation using the discrete shearlet transform[J]., 2008, 25(1): 25-46.
[22] 谢可夫, 许悟生. 量子衍生图像分解和边缘检测[J]. 计算机应用, 2013, 33(4): 1089-1091.
[23] 付游, 许悟生, 谢可夫. 基于量子理论的自适应图像融合规则[J/OL]. 计算机工程与应用, 2014: http://www.cnki.net/kcms/doi/ 10.3778/j.issn.1002-8331.1310-0273.html.
[24] Wang Z B, Ma Y D. Medical image fusion using m-PCNN[J]., 2008, 9(2): 176-185.
[25] Burt P, Adelson E. The laplacian pyramid as a compact image code[J]., 1983, 31(4): 532-540.
[26] Liu Z, Blasch E, Xue Z Y, et al. Fusion algorithms for context enhancement in night vision: a comparative study[J]., 2012, 34(1): 94-109.
Fusion for Infrared and Visible Light Images Based on Shearlet Transform and Quantum Theory Model
ZHANG Yao-jun,WU Gui-ling,LI Lei
(,,464000,)
In order to settle the drawbacks including high computational complexities and the unreasonable mechanism of traditional fusion methods for infrared and visible light images, a novel fusion technique for infrared and visible light images based on shearlet transform(ST) and quantum theory(QT) model is proposed in this paper. Due to the better competence of image information capturing, ST is utilized to conduct the multi-scale and multi-directional decomposition of source images. In addition, the fusion of low-frequency sub-images and a series of high-frequency ones is conducted by using QT. Finally, the final fused image can be obtained by using inverse ST.
shearlet transform,quantum theory,image fusion,infrared image,visible light image
TP182
A
1001-8891(2015)05-0418-06
2015-01-25;
2015-03-11.
张耀军(1979-),男,河南信阳人,硕士,讲师,主要研究方向为网络信息安全、图像智能信息处理等。

