基于偏最小二乘回归方法的木工刀具磨损分析与建模1)

耿绍辉( 东北林业大学，哈尔滨，150040)

在木材工业生产中，切削加工仍是木材与木质材料加工的重要方法，切削加工属于传统的机械加工方法，木材经切削加工能达到所需要的形状和表面，铣、刨、锯以及钻等都属于此种方法。切削加工的主要问题之一是刀具刃口因磨耗而变钝，在木材与木质材料的切削加工过程中，刀具刃口磨损状况是很复杂的。木工刀具刃口是否锋利是影响加工质量的重要因素，木工刀具磨损是木材切削过程中固有的现象，木工刀具磨损理论是研究刀具材料不断从刀具表面消失的过程。迄今为止，木工刀具磨损理论主要有:机械擦伤磨损、化学腐蚀磨损、电化学腐蚀磨损［1］。刀具磨损到一定程度时，切削过程不得不中断，增加换刀、磨刀的次数和机床的启动频率，降低了机床的使用效率。

影响木工刀具磨损的因素较多，很难建立一个准确适用的分析模型，多采用试验数据进行分析和建模，常用的方法有采用声发射的小波分析建立磨损模型［2］，或采用人工神经网络建立模型。这些方法各自存在一些缺点，小波分析方法利用对刀具磨损时各种信号的奇异性进行分析，受干扰信号的影响。人工神经网络对模型的解释性差，此外，这些方法都不具备变量筛选功能。笔者采用偏最小二乘回归(PLSR)理论，对木材切削过程木工刀具磨损试验数据进行分析和建模。偏最小二乘回归法可以进行变量筛选，有效地克服变量间的多重相关性，建立较为理想的刀具磨损的多元回归模型，还具有较好的可解释性。

1 偏最小二乘回归

偏最小二乘回归方法如下:设有单因变量Y∈Rn，自变量X=|x1，x2，…，xp|，xj∈Rn。偏最小二乘回归分别在X 和Y 中提取成分t1和u1，提取成分时为了回归分析的需要，要求满足［3］:①t1和u1应尽可能多地携带它们各自数据表中的变异信息;②t1和u1的相关程度能够达到最大。

在第一个成分t1和u1被提取后，偏最小二乘回归分别实施X 对t1的回归，以及Y 对t1的回归，如果回归方程已经达到满意的精度，则算法终止;否则，将利用X 被t1解释后的残余信息，以及Y 被t1解释后的残余信息进行第二轮的成分提取。如此往复，直到能达到一个较满意的精度为止。若最终对X 共提取了m 个成分t1，t2，…，tm，偏最小二乘回归将通过实施Y 对t1，t2，…，tm的回归，然后再表达成Y 关于原变量x1，x2，…，xp的回归方程，至此偏最小二乘回归建模完成。

根据上述原理，偏最小二乘回归的算法可归纳为如下步骤［4］:

①将X 与Y 进行标准化处理，得到标准化后的自变量矩阵E0和因变量矩阵F0。

②从E0中抽取一个成分，t1=E0W1，其中:

实施E0在t1上的回归:E0=t1P1+E1，即:E1=E0-t1P1，其中:

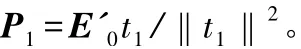
检查收敛性，若Y 对tj的回归方程已达到满意的精度，则进行下一步;否则，令E1=E0，回到第②步，对残余矩阵进行回归分析。

③在第h 步(h=2，…，m)，方程满足精度要求，这时得到各成分t1，t2，…，tm，实施F0在t1，t2，…，tm上的回归，得^F0=r1t1+r2t2+…+rmtm。

由于t1，t2，…，tm均是E0的线性组合，因此^F0可写成E0的线性组合形式，即:^F0= r1E0W*1 +，其中:I 为单位矩阵。

④按照标准化的逆过程，将^F0的回归方程还原为Y 对X 的回归方程。

经济犯罪案件现场重建的关键是现场分析。经济犯罪案件的现场分析是在现场访问和现场勘验搜集的各种认识经济犯罪行为的素材的基础上，去伪存真，对经济犯罪过程进行的逻辑推演。这个推演过程如果合乎经济犯罪当时的实际，并有相应的证据予以支持，侦查工作就实现了犯罪事实清楚、证据确实充分的目标。如果推演的犯罪过程并不符合犯罪当时的实际情况，或者并无足够的证据支持所推演的犯罪过程，则该案件的侦查工作就已经陷入僵局之中，需要回过头来，重新进行现场访问和现场勘验。

2 数据分析与建模

2．1 切削试验

切削试验是在木工铣床上进行的，刀具材料为K05 硬质合金，目前，硬质合金、高速钢仍然是木工刀具用得较多的材料，所以研究硬质合金钢、高速钢木工刀具的磨损特性具有实用价值。

试验中，工件选用中密度纤维板作为切削试验材料。中密度纤维板的厚度19 mm、长2 000 mm、宽200 mm，密度为0．72 g/cm3。

切削试验时，加工中密度纤维板边部，刀具切削形式为典型的铣削。在试验中，通过改变切削速度vc、进料速度vf、切削路径lc、进给量f、刀具后角α、刃磨角β 等相关参数，实测刀具磨损状况。例如，在其它切削条件一定的情况下，测量各种切削路径lc长度下刀具的磨损程度。

采用机械触针法测量木工刀具前后刀面的磨损量Sv，在不同的切削条件下，进行了多次切削试验。试验后，对所记录的各组数据进行处理、结果分析。

2．2 木工刀具磨损的PLSR 分析

在木材切削加工过程中，由于影响刀具磨损的因素较多，建模时首先要进行自变量的筛选。本研究中采用PLSR 方法进行变量筛选，以切削速度(vc)、进料速度(vf)、切削路径(lc)、进给量(f)、切削深度(ae)、刀具后角(α)及刃磨角(β)等7 个变量作为自变量，变量投影重要性指标VIP 值用来测度自变量集合对解释因变量集合的重要性作用大小，得出VIP 指标图和因子载荷(αi)图。变量的VIP 图中，7 个自变量对应的变量投影重要性指标VIP 值从0．61 到1．1，之间。因子载荷中，因子载荷最小为0．2，最大为0．38。

VIP 图和αi图显示，变量vf(进料速度)和变量f(进给量)的VIP 值和载荷因子系数α2和α4相对于其它变量来说要小，因此在模型中，可以忽略。这一结果对木材切削加工过程中对刀具磨损的在线实时估计和监控具有重要的意义。因为在加工过程中，进给量随着安装刀具的齿数的变化而变化，进料速度可能由于操作者的修调也不会保持为常量。根据上述分析，建模时可去除变量vf和变量f。根据切削力学和木工刀具磨损机理分析，可以忽略进给量对刀具磨损的影响，Pahlitzsch 研究表明，进给量(f)对刀具磨损(Sv)的影响，随f 增加，Sv呈下降趋势［5］。因此，PLSR 对实验数据的分析与理论分析结果是相吻合的，这表明PLSR 对木工刀具磨损影响因素的分析具有与切削理论一致的解释。可以认为，以切削速度(vc)、切削路径(lc)、切削深度(ae)、刀具后角(α)及刃磨角(β)作为自变量，以刀具磨损(S*v )值为因变量，对木工刀具磨损的建模和在线预报是较好的选择。因此，切削过程刀具磨损的模型可表示为

2．3 刀具磨损的PLS 回归模型

根据上述分析，以vc、lc、ae、α、β 作为自变量，S*v 作为因变量，对各种切削条件下的试验数据进行偏最小二乘回归迭代计算，求得

将S*v 按标准化的逆过程处理，即求出Sv。

3 数据检验与模拟

3．1 采用建模数据检验

用式(1)表示的切削过程木工刀具磨损的偏最小二乘回归模型，对建模所用数据覆盖的切削条件下的试验数据进行检验计算，得到对Sv的计算值，图1 给出了S′V计算值与Sv实测值对比的散点图。可以看出，大多数计算值与实测值是吻合的。

图1 对试验数据的检验结果

3．2 在线预报模拟

为检验模型(1)是否适用于自变量新测量值的情况，采用在新的不同试验条件下测量的自变量数据，模拟实际切削过程中在线估计刀具磨损的情况。模拟估计结果S′V与实测值(SV)对比的散点图见图2。可知，对于建模时没有覆盖的切削条件下的新测量样本点，由式(1)给出的回归模型仍可获得较好的估计预报值。

图2 在线预报模拟结果

4 结论

偏最小二乘回归(PLSR)方法是一种由数据样本进行建模的统计回归方法［6］。PLSR 方法可用于木材切削过程中刀具磨损情况的分析与建模，模拟在线预报表明该方法将可应用于切削加工过程中刀具状态的实时预报。采用PLSR 方法时，若选取合适的变量组合后，使得因变量和自变量第一主成分之间呈较好的线性相关性时，PLSR 模型可以获得较高的精度和可靠性，且PLSR 模型的表达式简单清晰，对切削过程中各因素对木工刀具的磨损量的影响有很强的解释意义，可以揭示出因变量与自变量之间的内在关系。通过图示，可以清楚地分析和选取适当的自变量，这是其它由数据进行建模的方法难以比拟的特点。从建模和预报的计算量考虑，PLSR 建模可以用直接计算法，也可以用迭代算法，其计算量都比较小，建模后进行预报的计算量更是很小，这对于进一步研究发展实时在线建模和模型修正算法有着重要的意义。

综上所述，PLSR 方法是一种简单可靠、解释性强、计算量比较小的建模方法，应用于木材切削过程中木工刀具磨损状态的建模、分析与预报，可获得比较满意的结果。

［1］ 曹平祥，王毅，周兆斌．木工刀具磨损机理及抗磨技术［J］．林产工业，2003，30(4):13-16．

［2］ 周兆兵，曹平祥．浅谈声发射的小波分析与木工刀具磨损检测［J］．木材加工机械，2002(6):1-5．

［3］ 王惠文．偏最小二乘回归方法及其应用［M］．北京:国防工业出版社，1999．

［4］ Geladi P，Kowalski B R． Partial least-squares regression:a tutorial［J］． Analytic Chimica Acta，1986，185(3):1-17．

［5］ Pahlitzsch G，Sandvo B E． Verschleiβuntersuchungen beim Fräsen von Faserhart-platten［J］． Holz als Roh-und Werkstoff，1970，28(7):245-254．

［6］ 刘强．刀具磨损的偏最小二乘回归分析与建模［J］．北京航空航天大学学报，2000，26(4):477-460．