关于平衡态下费米气体最小冷原子数目的讨论

刘艳萍

（山西职业技术学院电气工程与自动化系，山西太原030006）

（编辑 郭继荣）

0 引言

近年来，超冷量子气体理论是人们关注的研究领域之一.然而，人们研究超冷、弱相互作用的玻色气体的观点比较多，相比较而言，对超冷费米气体的研究理论却比较少[2].研究发现，玻色气体可以在极低温度下发生玻色-爱因斯坦凝聚现象（BEC），而费米气体却不能实现.但是，简并的费米气体系统可在极低温度下利用合适的条件将费米子形成库柏对，显现出一些宏观的量子效应，例如超导、超流等现象[2]，这一点与玻色系统极为相似.

1 超冷费米气体的研究现状

20世纪90年代以来，人们对超冷原子气体的特性进行了大量的研究，主要从玻色气体和费米气体两方面认识了相互作用的量子系统.而组成这两种量子气体的粒子间所表现出的弱相互作用会极大地影响量子系统的性质.自从人们在实验上获得碱金属原子的玻色-爱因斯坦凝聚体以来[1]，为了实现分子的BEC，科学家们针对超冷费米气体的性质做了大量的研究，而且取得了很大的进步.

费米子和玻色子的自旋差异使得它们有完全不同的特性，费米子具有半整数的自旋，它是一种像电子的粒子；玻色子具有整数自旋[4]209~210，它是一种像光子的粒子.任何两个费米子都不可能有相同的量子态，如像6Li或40K这样的费米子，即使在极低的温度下也具有或多或少不同的特性.物理学家们为了实现分子的BEC现象，采用了以下的方法：假设有两组费米气体，全都被束缚在光势阱中，且外加均匀的磁场，则可以利用磁场Feshbach共振的思想[1]来改变不同内部状态的原子之间的相互作用.当外加磁场的强度小于共振磁场的强度时，原子间的相互作用主要表现为排斥作用，不同内部态的原子会紧密结合在一起形成分子.在温度低于某一临界温度的条件下就会发生分子的BEC现象.具体来讲，就是物理学家将两个费米子转变成一个玻色子，即两个半整数的自旋结合组成一个整数自旋，成对的费米子起到了玻色子的作用，能在极低的温度下出现分子的BEC现象.利用这种方法，目前世界上已有多个实验小组成功地实现了分子的玻色-爱因斯坦凝聚现象.

之后不久，人们又很快通过实验实现了原子库柏对的凝聚体，并对它的性质做了大量的研究[1].对于费米冷原子系统，在外加磁场的强度大于共振磁场强度时，原子间的相互作用主要表现为弱吸引作用，并可配对形成弱束缚的费米原子对.在低温条件下，可形成费米原子对的凝聚体.目前，超冷简并费米气体正成为理想的研究强关联体系的实验对象，对于超冷简并费米气体的理论和实验研究正在进行，并处于蓬勃发展时期.这些研究将进一步深化原子物理、凝聚态物理等学科间的结合，同时会解决一些固态物理中尚存的问题.

2 平衡态下弱相互作用费米气体的最小冷原子数估算的思路及热容量的导出

要估算出低温下弱相互作用费米气体的最小粒子数的量级，我们必须先知道此时气体热容量的表达式，即热容量是非常关键的一个物理量，下面我们所做的工作就是利用热力学和统计物理的知识求出这个定容热容量的解析式，主要分无外磁场和谐振势约束两种情况来分别讨论.

2.1 无外磁场情况的弱相互作用费米气体的热容量

假设有一限定在体积V中的系统，由N个自旋为1 2、弱相互作用的费米子组成，其能谱为：

上式中的p为量子态的动量；m为单个粒子的质量；ħ＝h 2π，其中h为普朗克常量；N↑、N↓分别表示自旋为向上、向下的总粒子数；np↑、np↓分别表示处于动量为p的量子态上且自旋为向上、向下的粒子数目；ɑ为波散射的长度（存在于粒子之间的相互作用的），它满足以下式子所表示的弱相互作用的条件：

p

根据式（1）可得到该系统的配分函数[2]为：

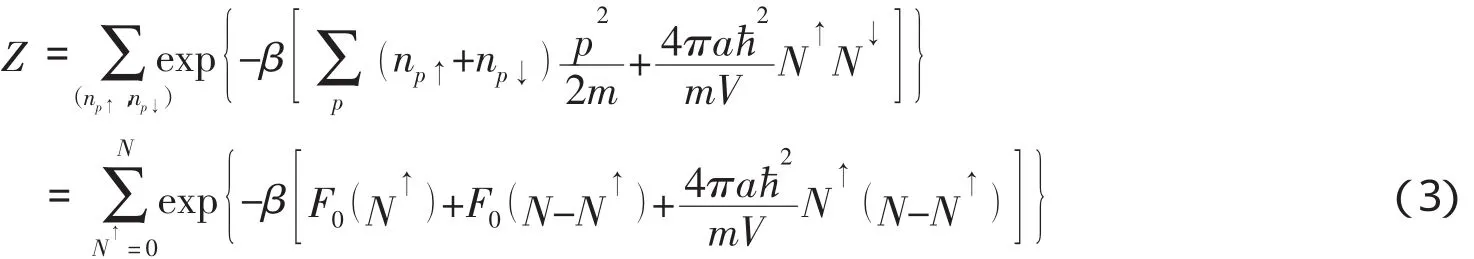
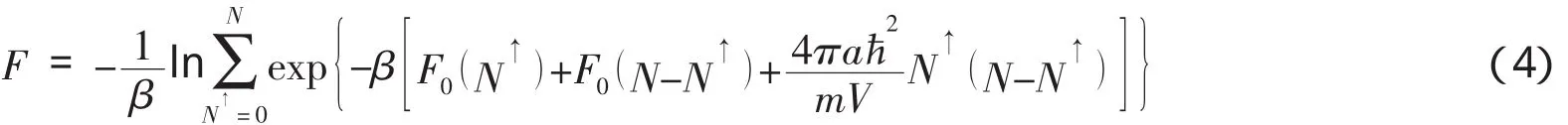
对于弱相互作用的费米系统，总有kF0ɑ＜π 2（其中kF0为对应于费米能级EF0的波数），且N↑＝N 2时（4）式中的求和项最大，故（4）式可表示为：，再由（3）式得到费米系统的自由能[2]为：

再由以上的式子可求出系统的化学势、内能和定容热容量[2]，它们分别表示为：

我们仅讨论低温时系统的这几个热力学量，经计算得低温极限下系统的化学势、内能和定容热容量分别为：

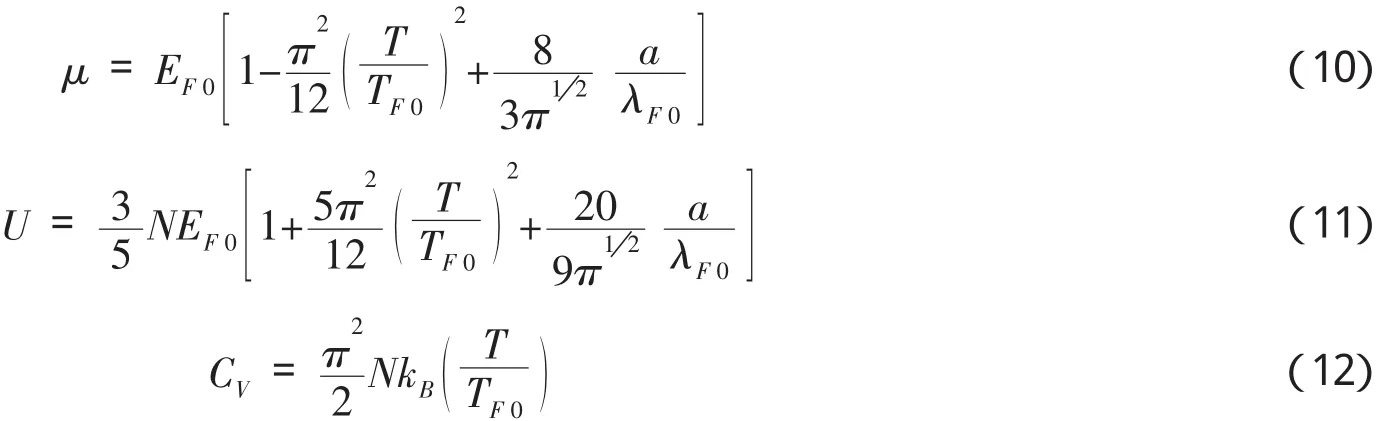
上式中的EF0＝ （ħ22m）（3π2n ）23为理想费米系统的费米能[5]87~92，TF0＝EF0kB为费米温度，λF0＝

2.2 谐振势约束情况的弱相互作用费米气体的热容量

现讨论一约束在谐振外势中的弱相互作用的费米气体，设束缚在光势阱中的费米原子感受到的外势可近似为如下的谐振势：

式中的x、y和z为费米粒子在三个坐标轴上的坐标，ωx、ωy和ωz为谐振势沿三个坐标轴的角频率.处于外势中的非均匀系统达到平衡状态时，系统的化学势可表示为：

同理，非均匀系统空间r处的能量密度ε（）

r[2]可表示为：

再通过数学运算我们可求出外势中弱相互作用费米系统的粒子数密度n（）r和能量密度ε（）r的表达式分别如下：

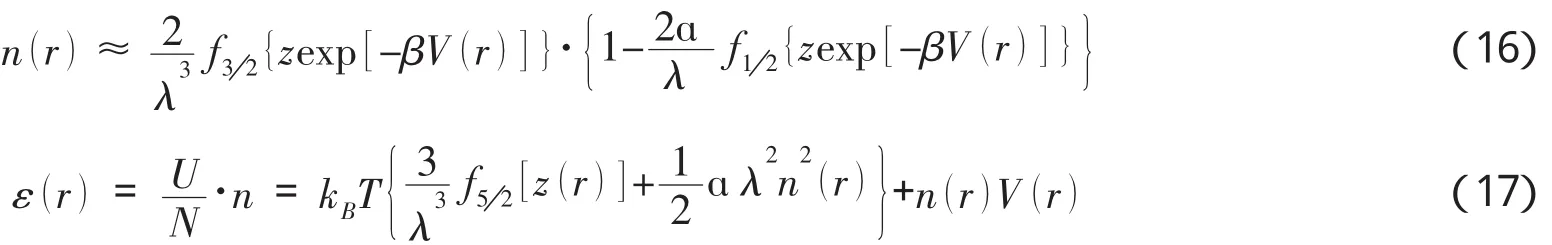
上式中的z为系统的无相互作用逸度，现将化学势μ和内能U分别表示为z的函数[2]，结果是：

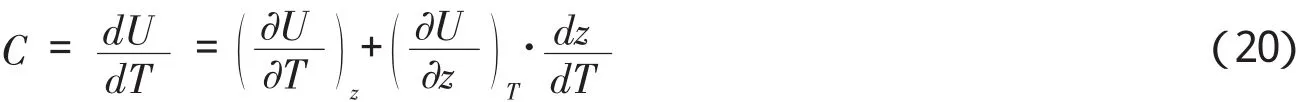
接下来我们着重讨论低温时弱相互作用费米气体的这几个热力学量，将以上式子通过大量的运算可得到超低温下、弱相互作用的费米气体在谐振势约束条件下的化学势、内能和热容量的解析表达式[2]分别为：

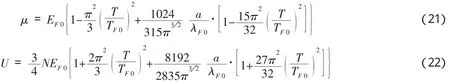
再由下式求解系统的热容量：

3 热平衡状态下弱相互作用费米气体的最小冷原子数的估算

3.1 估算方法

超低温下，一个系统若能满足热力学第三定律，且温度的涨落必须足够小[3]，这是一个系统能够达到热力学平衡状态必备的条件.

由度的相对涨落公式[4]得到温度的涨落公式：

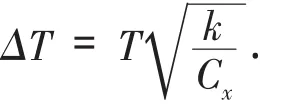
由于经典粒子系统的热容量Cx与粒子数N成正比，即Cx∝N k[4]，故相对温度涨落当相对温度涨落趋近于零时，系统达到平衡状态，此时粒子数很大[3].

表示每个粒子的平均热容量，则有低温下系统达到平衡态时所具有的最小粒子数为：

以下部分将按照这种讨论方法分别求出两种情况下弱相互作用下费米系统最小粒子数的量级.

3.2 具体估算过程

3.2.1无外磁场的情况

由式（12）和式（24）得到无外加磁场时，超低温的弱相互作用的费米气体单个粒子的平均热容量为：

将式（26）代入式（25）得

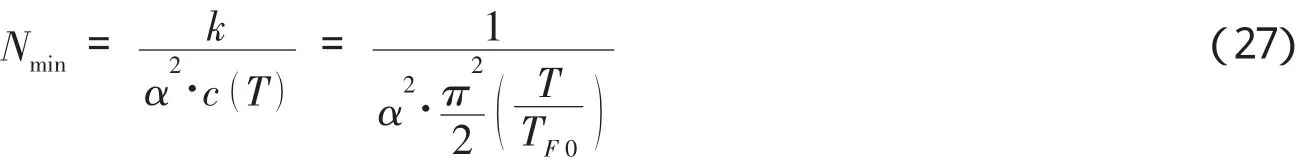
由此式可知，低温下、无外磁场情况下的弱相互作用费米气体，系统要处于热力学平衡态时所需的最小粒子数目会随温度的降低而迅速增加，即低温温度越低，系统的粒子数目Nmin将越大.

在此，近似给α取一个很小的定值，如α＝0.001，π＝3.14，经查得得出Nmin≈2.03×107个，因此，低温下、无外磁场情况下的弱相互作用费米气体要达到热力学平衡状态，至少需要数目量级为107的粒子数存在.，将这几个数值代入式（27）

3.2.2谐振势约束的情况

由式（23）和式（24）可得到有谐振势约束时、超低温的弱相互作用的费米气体单个粒子的平均热容量为：

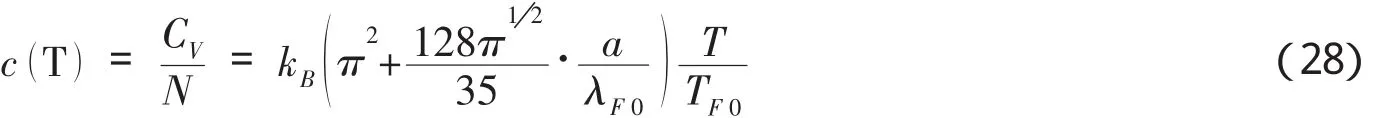
将式（28）代入式（25）得：

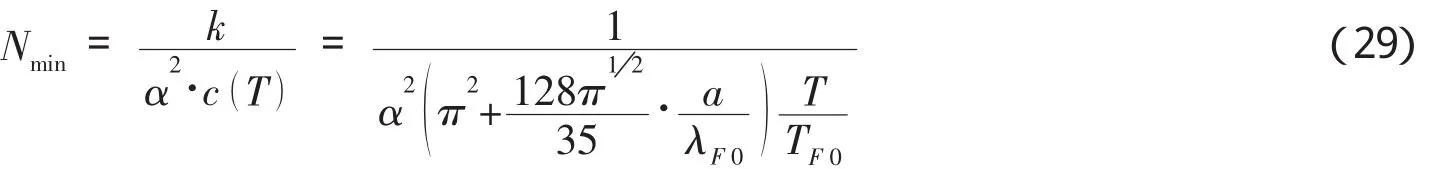
由此式可知，低温下、受谐振势约束的情况下的弱相互作用费米气体，系统要达到热平衡态时所需的最小粒子数会随温度的降低而迅速增加，即低温温度越低，系统的粒子数目Nmin反而越大.

4 结论

文章主要研究了超低温下、处于热力学平衡态的费米气体可能具有的最小的粒子数，并试着应用统计物理等知识得到费米气体的定容热容量Cr的解析表达式，再利用热容量与平衡态下冷原子的最小数目Nmin之间的关系分析讨论了弱相互作用费米气体在无外磁场和谐振势约束两种情况，给出了对这种系统的最小粒子数量级的估计.由此可知，在低温极限下，对于一个弱相互作用费米气体系统，无外磁场情况下至少要有量级为107的粒子才能构成一个热力学系统，而谐振势约束情况下则至少需要量级为105的粒子.

［1］熊宏伟，吕宝龙.超冷费米气体研究的新进展［J］.物理学进展，2005，25（3）：296~297.

［2］苏国珍，陈丽璇.弱相互作用费米气体的热力学性质［J］.物理学报，2004，53（4）：985~987.

［3］X.Wang，Q.H.Liu.Dependence of the existence of thermal equilibrium on the number of particles at low temperatures［J］.American Association of Physics Teachers，2007，75（5）：431~432.

［4］冯玉广，李士.热力学与统计物理学导论［M］.北京：中国科学技术出版社，1993.

［5］梁希侠.高等统计力学导论［M］.呼和浩特：内蒙古大学出版社，2000.