特殊的p2m+1阶capable群性质研究

李志秀

（晋中学院数学学院，山西晋中030619）

（编辑 郭继荣）

0 引言

给定了一个群G，若能够找到另外的一个群H，H Z（H ）≅G，则称G为capable群.最早是在1938年Baer开始对中心商问题研究，后来P.Hall和M.Hall等学者都对此问题做过研究.近年来也有一些学者取得了新的结果.2003年，Michael R.Bacon和Luise-Charlotte Kappe借助于他们对二元生成的类2的p（p＞2）群的分类结果，在文[2]给出了此类群是capable群的充要条件.此外，还给出了类2的p（p＞2）群是capable群的一个必要条件.2005年，Arturo Magidin利用幂零积的概念对capable群进行研究，推广了P.Hall和Baer的结果，给出了类为k的群是capable群的必要条件，并且在文[3]给出了二元生成的类为2的p（p＞2）群是capable群的充要条件的另一种证明.但是，迄今为止，对于这个问题的研究总的来看还是不够的，还有必要进一步探索.

1 主要结果

引理1.1 （[1]）设G是有限p-群.

（1）若 c（G ）＜p，则G正则.

（3）若p＞2且G′循环，则G正则.

（4）若 exp（G ）＝p，则G正则.

引理 1.2 （[1]）设 G 是有限正则p-群，a，b∈G，s，t为非负整数，则

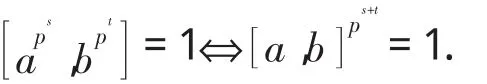
定理1.3 设m是正整数，p是素数，且满足p≥5.则群

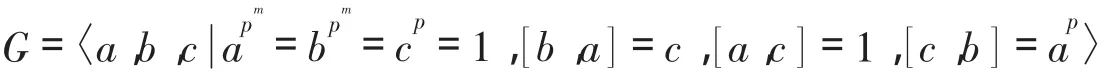
是capable群当且仅当m≤2.

证明 “⇒”因为c（G ）＝3，所以若存在p群H，使得H Z（H ）≅G时,有c（H ）＝4，由引理1.1可知H正则，H为正则p群的中心商.设.则cp∈Z（H ），由引理 1.2可知，即，若 m大于 2，则矛盾与.所以 m≤2.

“⇐”m＝1时，G是 p3阶群，存在

事实上，H可由交换群〈a〉×〈e〉出发，依次添加两个元素c，b做两次循环扩张得到.可设，在 A 中规定映射：

则ab＝a，C诱导A的一个p阶自同构，得到B，

在B中规定映射：

则ab＝a，b诱导B的一个p阶自同构，可得到H.Z（）G ＝〈e〉，H Z （ ）

H≅G.G是capable群.m＝2时，令

［1］徐明曜.有限群导引：下册［M］.北京：科学出版社，1999.

［2］M.Bacon，L.C.Kappe.On capablep-group of nilpotency class two［J］.lllinois Journal of Mathematics Volume，2003（47）：49~62.

［3］Magidin.Arturo.Capability of nilpotent productsof cyclic groups［J］.J.Grpup Theory，2005，8（4）：431~452.