氢原子的概率密度分布

宫建平

（晋中学院信息技术与工程学院，山西晋中030619）

（编辑 郭继荣）

作为量子力学的一个经典问题，氢原子一直是人们关注的对象，近年来关于氢原子概率密度在空间分布的讨论一直持续不断[1～10].氢原子的薛定谔方程是可以严格求解的为数不多的例子之一，能够得到波函数严格的解析解，从而可以精确描绘出其电子的径向、角向及整体的运动情况.近年来，随着计算机技术的迅速发展，结合计算机绘图软件的强大功能，通过对氢原子电子分布的概率密度图像的描绘，对氢原子中运动的图像描绘更加直观.近年来，人们利用数学软件绘制了氢原子波函数的平面和立体图形[1]，以及应用三维重构技术实现了氢原子基态和各个激发态电子云的外观图[2]，通过数值计算分析了氢原子中电子概率密度的分布情况，并进行了详细的讨论[3～4].

本文首先对氢原子的径向概率密度分布展开讨论，然后给出了氢原子的角向概率分布图像，最后利用概率等值线图和等概率曲面图给出了氢原子的电子概率的三维空间分布图像.从而对氢原子的运动形态有了更加直观的印象，并澄清了关于氢原子角向概率分布存在的一些模糊认识[11]68.

1 径向概率密度分布

当氢原子处于 ψnlm（r，θ，φ）态时，电子在（r，θ，φ ）点的周围的体积元dτ＝r2sinθdrdθdφ 内的概率是

将此式对θ从0→π，对φ从0→2π积分，并注意Ylmθ，（）φ是归一化的，我们便得到半径r到r→r+dr球壳内找到电子的概率是

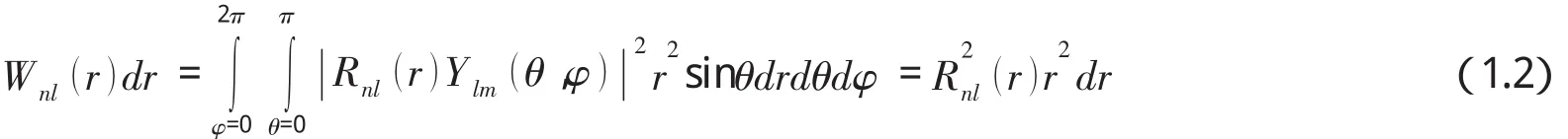
粒子的径向函数为

式中Nnl是归一化常数.归一化常数为氢原子的径向概率密度为：

注意（1.5）式给出的径向概率密度是指半径r到r→r+dr球壳内找到电子的概率，而并不是说在半径为r的球面上真实空间的概率密度.比如我们熟知的玻尔半径，是指在r＝ɑ的球面上总的概率取极大值，而不是在r＝ɑ的空间点上取极值.而空间沿径向真实的概率密度值应该由R2nl（r）给出.为了考察氢原子的概率密度在三维空间的真实分布，同时为了比较Wnl（r）与R2nl（r）的不同，下面给出不同的n，l分别由Wnl（r）、R2nl（r）绘制的曲线.比较发现两者存在明显不同.特别是W10（r）在rɑ＝1处（即玻尔半径处）有一极大值，如图1.3所示，而R210（r）只在rɑ＝0处有一最大值，如图1.1所示.再者Wnl（r）在原点总是为零，而R2nl（r）则不一定，这是因为Wnl（r）＝R2nl（r）r2.

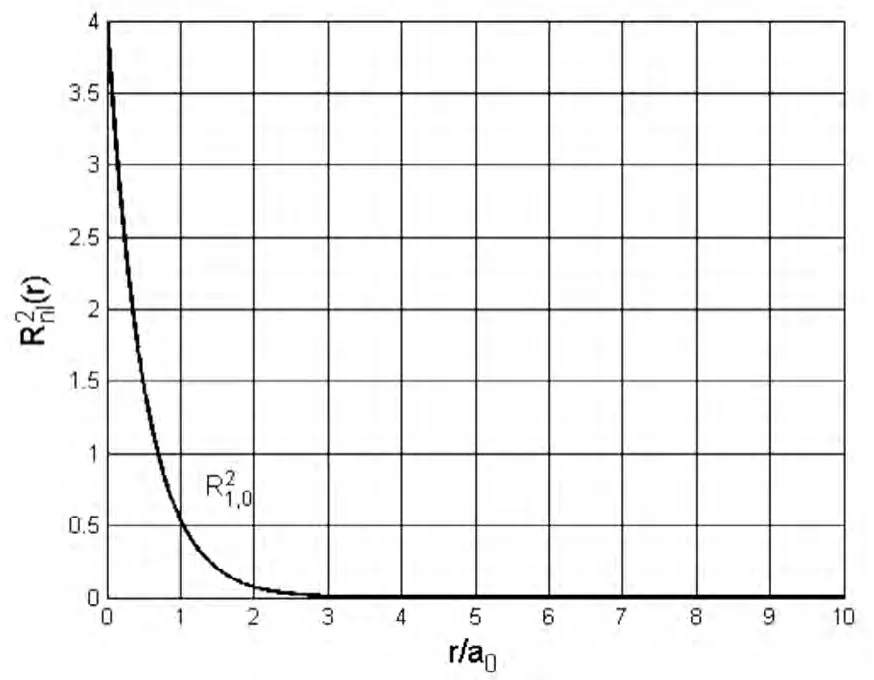
图1 .1 取n＝1，l＝0时的R210（r）分布曲线

图 1.2 分别取n＝2，l＝0，n＝2，l＝1时的 R220（r）（实线）和R221（r）（点线）分布曲线

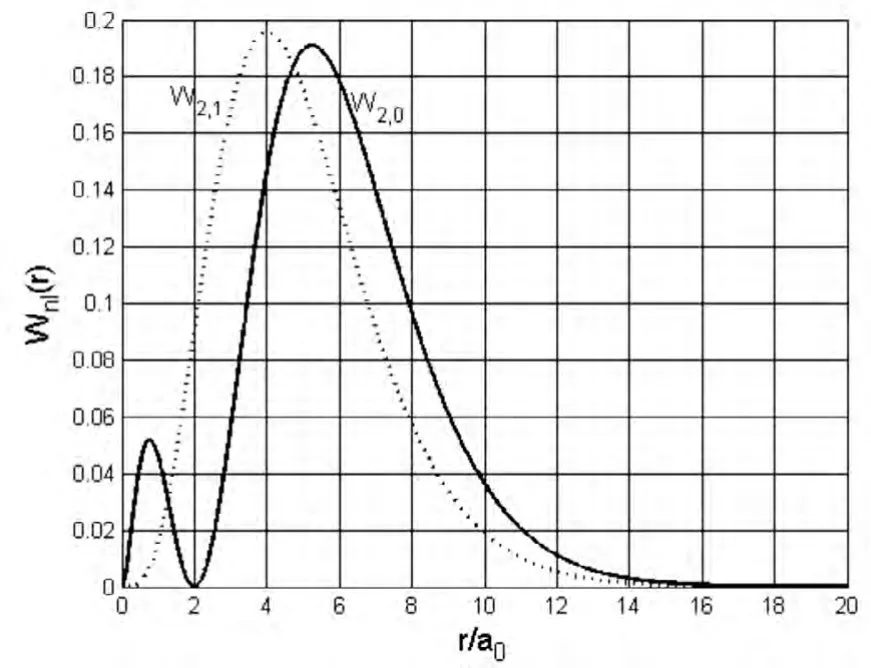
图1 .4 分别取n＝2，l＝0，n＝2，l＝1时的 W20（r）（实线）和W21（r）（点线）分布曲线

图1 .3 取 n＝1，l＝0时的 W10（r）分布曲线

2 角向概率密度分布

氢原子的角向波函数是球谐函数Ylmθ，（）φ

式中Pml（cosθ）是缔合勒让德多项式，Nlm是归一化常数.l表征角动量的大小称为角量子数，m则称为磁量子数.由（2.1）式可知，对应于一个l的值，m可以取（2l+1）个值.

将（1.1）对r从0到∞积分，并注意到Rnl（r）是归一化的，我们得到电子在方向（θ，φ）附近立体角dΩ＝sinθdθdφ 的概率是

因此得到

由于Wlm与φ角无关，所以这些图形是绕z轴对称的立体图形.例如，在l＝0，m＝0时，概率是

它与θ无关，所以在角向概率图是一个球面.又如l＝1，m＝±1时的概率

在θ＝π2（不论φ取任何值）有最大值，在极轴方向θ＝（）

0 的值为零.而 l＝1，m＝0 时，

情况则恰好相反，在θ＝0，π处概率有最大值，θ＝π 2处概率为零.

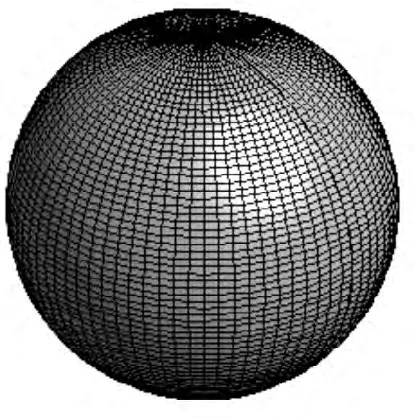
图2 .1 取l＝0，m＝0时s电子的角向概率密度分布的空间图像

图2 .3 取l＝1，m＝±1时p电子的角向概率密度分布的空间图像

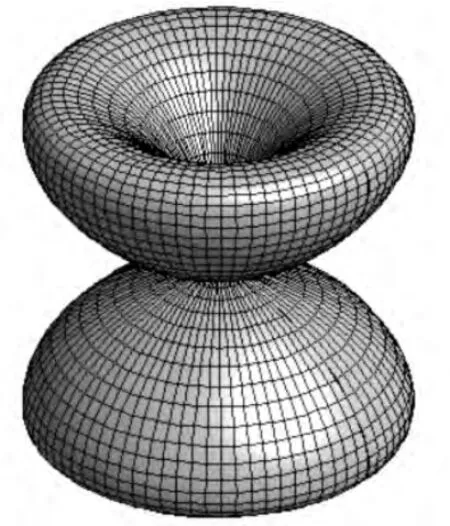
图2 .5 取l＝2，m＝±1时d电子的角向概率密度分布的空间图像

图2 .2 取l＝1，m＝0时p电子的角向概率密度分布的空间图像

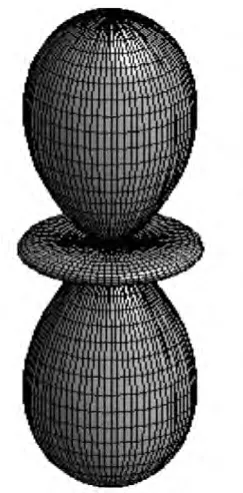
图2 .4 取l＝2，m＝0时d电子的角向概率密度分布的空间图像

图2 .6 取l＝2，m＝±2时d电子的角向概率密度分布的空间图像

利用（2.3）式可绘制出不同l，m时的Wlm（θ，φ ）图，即为角向概率密度分布图.比如l＝0，m＝0的s电子的角向概率密度分布，它的分布是球对称的.l＝1，m＝0，±1的p电子的角向概率密度分布，l＝2，m＝0，±1，±2的d电子的角向概率密度分布，它们如图2.1~图2.6所示.它们都是关于z轴旋转对称的.而教材中的角向概率分布图，其实是角向概率密度平面极坐标图形[11]，并非角向概率密度三维立体分布图形.此处的三维图形可以看作平面极坐标图形绕z轴旋转形成的.

3 氢原子的概率密度空间分布图像

氢原子的定态波函数是处于这个态时ψnlm与n，l，m三个量子数有关.

知道了氢原子的波函数，就可以进一步讨论氢原子内电子在空间各点的概率分布.当氢原子处于ψnlm（r， θ ，φ）态时，电子在（r，θ，φ ）点的周围的体积元dτ＝r2sinθdrdθdφ 内的概率是

根据（3.2）式可以绘制出氢原子空间的概率密度分布图像.

10氢原子处于ψ100（r，θ，φ）态时的概率密度空间分布图像.

从图1.1可以看出R210（r）只有在rɑ0＝0处有一极（最）大值，而从图2.1可以看出 ψ100（r，θ，φ）2角分布是球对称的，所以我们可以推测出处于基态的氢原子的概率分布应该如图3.1a所示，在xoz平面上xɑ0＝0，zɑ0＝0点处概率密度取最大值，并非在玻尔半径r＝ɑ0处取极大值.虽然在玻尔半径r＝ɑ0的球面上，概率密度并非取极大值，但径向概率密度Wnl（r）＝R2nl（r）r2是指在玻尔半径附近的球壳找到粒子的概率是最大.由于 Wnl（r）＝R2nl（r）r2与r2成正比，所以虽然在原点处电子的概率密度取极大值，但Wnl（r）＝R2nl（r）r2仍然为零，在玻尔半径r＝ɑ0（即rɑ0＝1）的球面上虽然电子的概率密度并非取极大值，但Wnl（r）＝R2nl（r）r2却为极大值.由图观察明显看到处于基态的氢原子的概率密度分布呈球对称分布.注意R210（r）的极大值为R210（0）＝4，而W100（r，θ，φ）的极大值为W100（r，θ，φ）＝1π＝0.3183.由于基态氢原子各向同性，且相同的r概率密度相同，所以等概率密度曲面为一球面，如图3.1b.

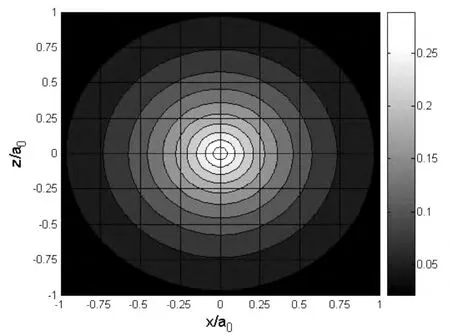
图3 .1a 取n＝1，l＝0，m＝0时基态氢原子电子的概率密度分布在xoz平面的等高线

图3 .1b 取n＝1，l＝0，m＝0时基态氢原子电子的概率密度相同的点组成的曲面

20氢原子处于ψ200r，θ，（）φ态时的概率密度空间分布图像.

图3 .2a 取n＝2，l＝0，m＝0状态时氢原子电子的几率密度分布在xoz平面r a0＜1.5区域的等值线图

图3 .2b 取n＝2，l＝0，m＝0状态时氢原子电子的几率密度分布在xoz平面r a0＞1.5区域的等值线图

图3.2c 取n＝2，l＝0，m＝0状态时氢原子电子的等概率密度面,可以看出它是一些同心球面，此时只可以看到两个等概率面.

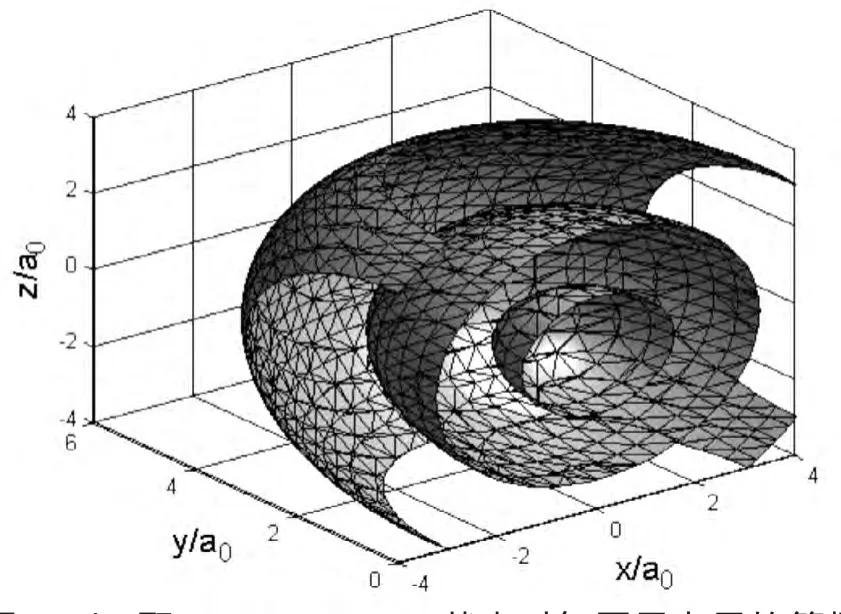
图3 .2d 取n＝2，l＝0，m＝0状态时氢原子电子的等概率密度面,可以看出它是一些同心球面,从此剖面图只可以看到三个等概率面

处于ψ200r，θ，（）φ态的氢原子仍然具有球对称性，即各向同性.从图1.2可以看出在原点和rɑ0≈4处径向概率存在两个极大值.但在原点处的最大值比rɑ0≈4处的极大值高出几十倍，所以很难在一张图中表示，故用图3.2 a、图3.2b分别表示rɑ0＜1.5和rɑ0＞1.5区域的等概率线图.在rɑ0等于零及rɑ0约为4处取极大值.由于概率分布各向同性，所以此时的等概率面仍然是一球面，从R220（r）曲线看，只要概率密度值取得合适（足够小）可以有三个不同的r满足它，所以此时的等概率面应当是三个不同半径的同心球面，从图3.2c只可以看到两个同心球面，从图3.2d可以看到三个同心球面.这与我们的分析结论一致.

图3.3a 取n＝2，l＝1，m＝0时氢原子电子的几率密度分布在xoz平面的等值线图

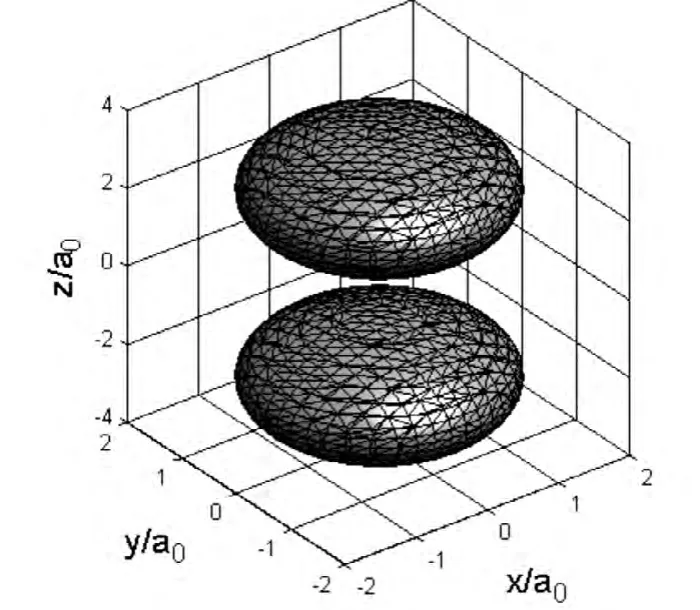
图3 .3b 取n＝2，l＝1，m＝0时氢原子电子的概率密度相同的点组成的曲面

30氢原子处于ψ210r，θ，（）φ态时的概率密度空间分布图像.

处于ψ210（r，θ，φ）态的氢原子其径向概率分布如图1.2中点线所示，R221在rɑ0≈2处有一极大值，其角向分布如图2.2，在θ＝0，π处概率有最大值，θ＝π 2处概率为零.这些分析的结论，可从氢原子在xoz平面的概率分布等值线图3.3a得到印证，而此时的等概率曲面图3.3b即为图3.3a中某一条等概率线绕z轴旋转得到.

40氢原子处于ψ21±1r，θ，（）φ态时的概率密度空间分布图像.

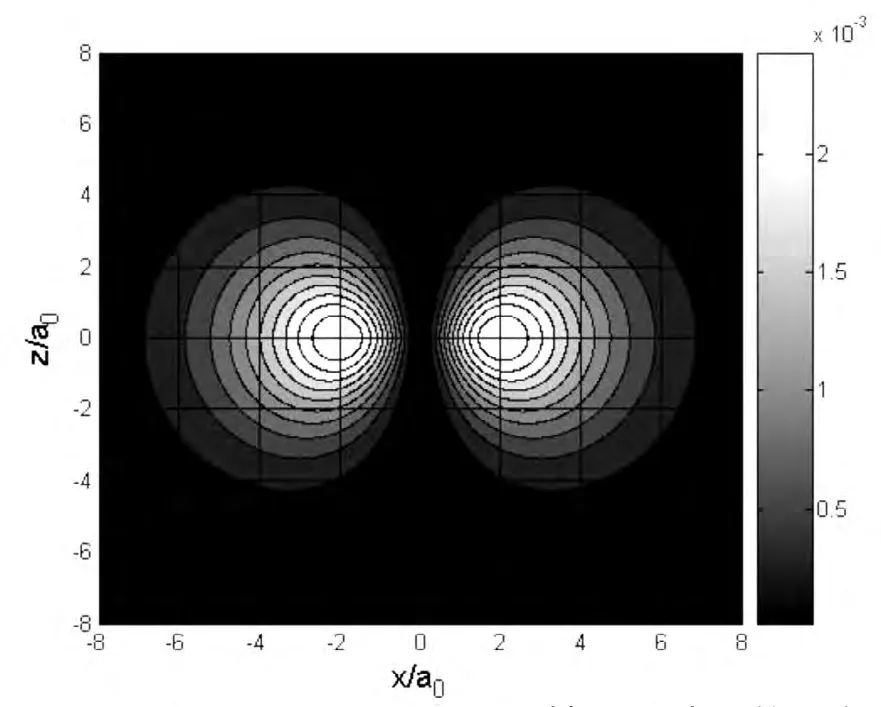
图3 .4a 取n＝2，l＝0，m＝±1时氢原子电子的几率密度分布在xoz平面的等值线图

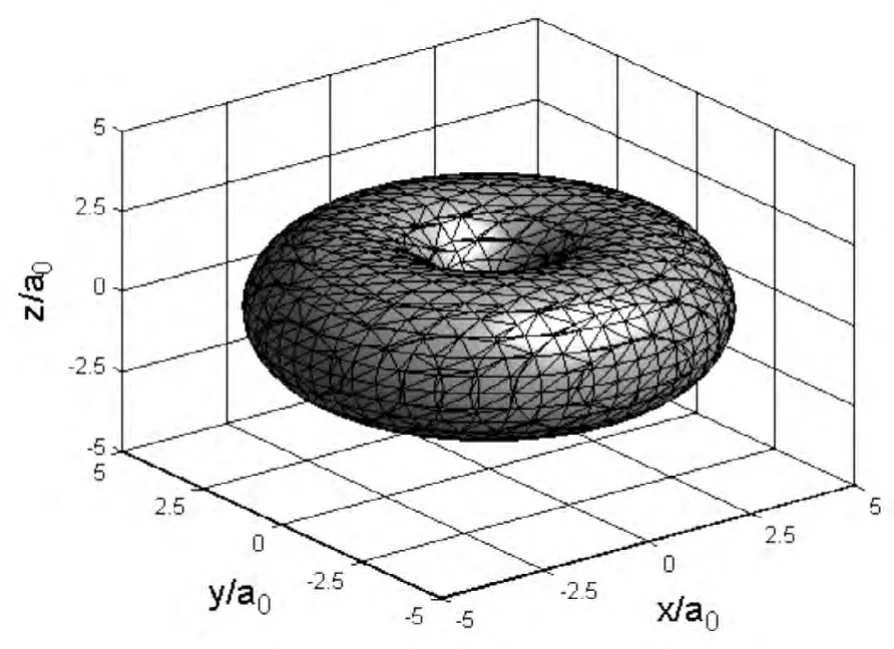
图3 .4b 取n＝2，l＝0，m＝±1时氢原子电子的概率密度相同的点组成的曲面

处于ψ21±1（r，θ，φ）态的氢原子其径向概率分布如图1.2点线所示，R221在rɑ0≈2处有一极大值，其角向分布如图2.3所示，与处于ψ210（r，θ，φ）态的情况则恰好相反，在 θ＝0，π处概率有最大值，θ＝π 2处概率为零.处于ψ21±1（r，θ，φ）态的氢原子在xoz平面的概率分布等概率线如图3.4a所示，将此图中的某一条等值线绕z旋转一周即构成等概率曲面，如图3.4b所示.

4 总结

认识氢原子概率密度的空间分布要从概率的径向（此处是指R2nl（r） 和角向分布两方面入手，空间某一点的概率由二者决定.比如空间某一点取极大值，必须是R2nl（r）在此半径的球面上取极大值，同时要求角向概率在此方向上也取极大值才行，两者缺一不可.再者考虑概率分布与φ角无关，所以空间的概率分布是关于z轴旋转对称的.所以将xoz平面或yoz平面的等概率线绕z轴旋转一周即可得到空间的概率分布.按照此方法可以将氢原子的其他状态的空间概率分布绘制出来，但鉴于篇幅关系在此不再讨论.

［1］卢志恒，费义艳，李雪春.量子力学可视化的计算机辅助表述——电子云、壳层结构以及共价键的三维重构［J］.物理，2001，30（4）：241~246.

［2］张建华，苏育志，宋建华，郭海燕.用 origln6.0绘制波函数平面图形［J］.计算机与应用化学，2003，20（4）：467~470.

［3］李金海，方恒忠，李子良.氢原子电子云密度分布分析［J］.大学物理，2004，23（3）：13~17.

［4］刘建军，高峰，华厚玉.氢原子波函数三维空间分布在MATLAB中的实现［J］.淮北煤炭师范学院学报，2004，25（4）：31~33.［5］邓明森.基于计算机仿真技术的氢原子电子云图模型［J］.贵州教育学院学报：自然科学，2005，16（2）：35~37.

［6］赵旭光，刘晓军.用 Matlab获得氢原子的电子云图像［J］.齐齐哈尔大学学报，2006，22（5）：98~100.

［7］马德明，仇海强，施卫.氢原子电子云分布的可视化分析［J］.西安理工大学学报，2007，23（2）：149~152.

［8］杨 林.氢原子电子概率分布可视化及其性质研究［J］.绥化学院学报，2009，29（2）：186~188.

［9］赵云芳，周战荣，李育新.氢原子电子云的计算和可视化分析［J］.大学物理，2009，28（9）：51~54.

［10］陆云清，刘洋，邓玲玲.氢原子电子云空间分布的可视化［J］.物理与工程，2009，19（5）：8~10.

［11］周世勋.量子力学教程［M］.北京：高等教育出版社，1979．

（SchoolofInformationandEngineering，JinzhongUniversity，JinzhongShanxi，030600China）