非规整报警的相关性分析方法

李元，章展鹏，徐鸣远，陈丙珍，赵劲松

（化学工程联合国家重点实验室（清华大学），北京 100084）

引言

报警系统建立的目的是防止化工生产过程中出现紧急停车、异常工况而引起经济损失。但由于分布式控制系统（distributed control system，DCS）的出现，增设报警位点成本极低，这直接导致工厂报警数量急剧上升，无效报警过多，报警泛滥现象频繁发生[1]。国际标准推荐操作员每10 min接受的平均报警数不超过1次，异常工况下10 min内的报警数不超过10次[2]，而各领域报警系统的实际现状与此标准差距很大。报警管理因此具有非常重要的地位。

随着化工生产过程耦合度的不断提高，相关报警也随之增多。Rothenberg[3]指出，相关报警可分为序列报警与非序列报警，序列报警为某一位号发生报警所引起的固定报警序列，非序列报警为接连出现但延迟时间不固定的多个报警。对于相关报警的分析有利于报警系统更加简洁、系统地展示报警信息，同时有助于操作员在此基础上进行报警原因分析、异常工况预测等工作。

Izadi等[4]提出报警系统分析、设计、管理的标准与方法，指出合理的报警系统应在漏报率、误报率、报警延迟等指标中做出平衡。Zhu等研究了重复报警的处置方法[5]，并提出动态报警管理策略[6]。Choi等[7]提出了计算0、1序列之间的相似度，并利用凝聚层次聚类算法进行分组的聚类方法。接下来的研究工作均在此框架下展开。Chen等[8-10]提出报警相似度色彩图（alarm similarity color map，ASCM）概念，认为它可以成为表征报警相似度的图形工具。此外，有研究者对现有的相似度函数进行总结归纳，提出了相似度函数性能的评价标准[11-12]，并指出可以使用互相关函数算法作为计算报警相似度的方法[13]。

现有的方法在处理序列报警时效果良好，但面对非规整报警时，传统方法难以挖掘其相关性。这是因为现有方法利用整体平移0、1序列的方法引入延迟[11]，却没有考虑到相似报警接连出现但延迟时间不固定的情况。其次，现有的方法均假定两个报警位点的相关性对称[12]，即报警位点A对B的相关性等于B对A的相关性，但在实际生产中，会出现报警A必然导致报警B但报警B未必导致报警A的情况。这种非对称的相关性是现有方法未考虑到的。

本文在传统的基于凝聚层次聚类的报警相关性挖掘方法基础上，提出了非规整报警相关性计算方法，弥补了传统方法难以处理延迟时间变化与非对称情况的不足。同时，为了能够让不同位点、不同装置之间的相关性结果具有可比性，提出以概率形式表示报警位点之间的相关性大小的方法。最后，利用仿真案例与工厂真实生产案例验证本方法的有效性。

1 相关性计算方法改进

1.1 生成报警0、1序列

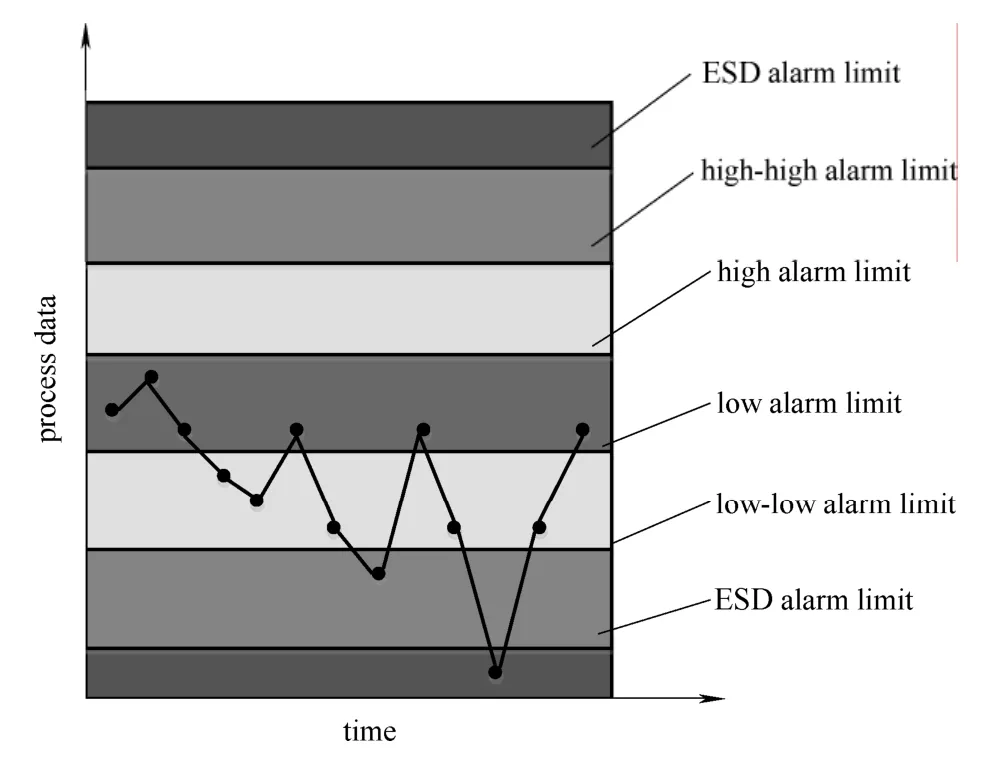
图1 典型的过程变量报警示意图Fig.1 Typical sketch for process variable alarm

如图1所示，在实际工业生产中，每一个位点设置有不同级别的报警限，当位点变量值超过报警限后，便会触发相应级别的报警。为表征这种随时间变化的报警序列，用“0”表示正常状态，“1”表示超限（包括高报警限与低报警限）的报警状态。以超出上限的情况为例，记过程变量序列为x(n)，报警序列为xalarm(n)，高报警限为xthreshold，则可以表示为

这样的表征方法虽可以准确反映变量是否处于报警状态，但在报警泛滥现象出现时，“1”的数量会急剧增多，导致需要挖掘的相关性被无效信息淹没。因此，在实际应用中采用另一种方法，即仅将报警由正常变为超限的时刻记为“1”，其余均记为“0”

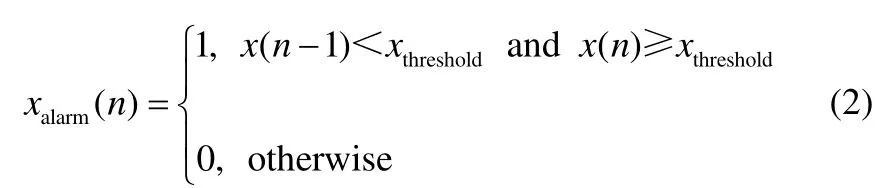
1.2 凝聚层次聚类算法

在得到各个位点的 0、1报警序列后，可利用相似度函数计算得到位点两两之间的相似度大小。接下来，利用凝聚层次聚类算法将位点之间的相似度聚类，得到若干组互相关联的报警位点，并利用ASCM图可视化地展示结果。

凝聚层次聚类算法是聚类算法的一种，由Johnson[14]首先提出，具体操作步骤如下：

（1）假设有N个对象，每个对象算作一个类C，得到类集合 {C1,C2,… ,CN}，计算每对类两两之间的相似度，相似度计算方法可以自行定义，常见的是利用相似度函数进行计算（见1.3节）；

（2）将相似度最大的两个类Ci和Cj合并成一个新类CN+1；

（3）用新类CN+1替换掉Ci和Cj，得到新的类集合，且新集合中类的数量比旧集合中类的个数少1个；

（4）重新计算新集合中新类CN+1与其他类之间的相似度；

（5）重复步骤（2）～步骤（4），直至步骤（4）中计算得到的相似度低于设定阈值。最终得到的类集合即是聚类结果。

在步骤（4）中，需要定义新类CN+1与其他类之间的相似度如何计算。在本文中，计算两个旧类Ci和Cj与其他类Ck之间的相似度，并将结果中的最大值作为新类CN+1与Ck的相似度。

将聚类后各对象之间的相似度记为维度为N的相似度矩阵，且同一类中的对象排列在对角线附近。以颜色的深浅表示相似度大小，则可以得到ASCM图。以图2为例，其中1～10表示10个对象，经过凝聚层次聚类后得到 4个类，并且C1= { 8}，C2= { 1,6,7,4}，C3= { 3,9}，C4= { 10,2,5}。

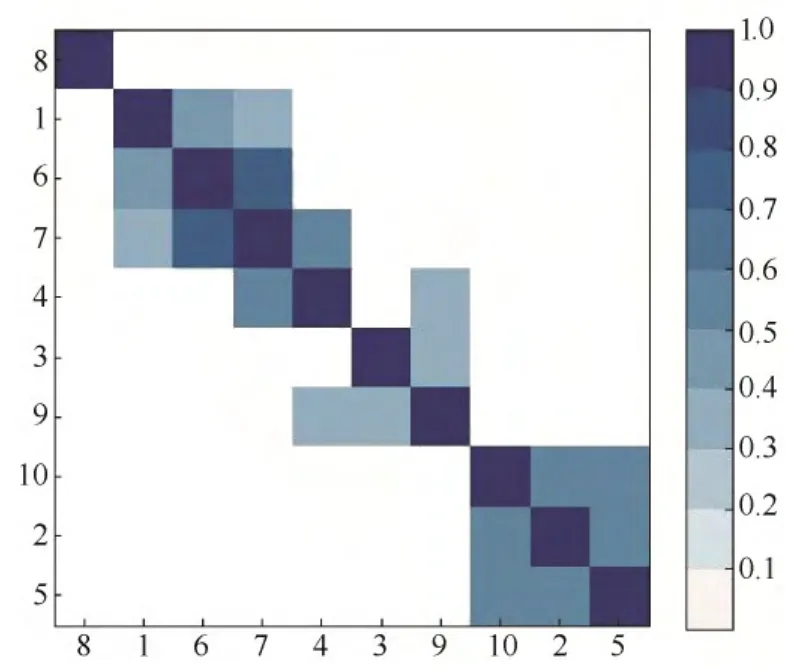
图2 ASCM示意图Fig.2 Alarm similarity color map

1.3 传统相似度函数

Yang等[11]指出，针对报警系统性能最好的相似度函数为 Jaccard函数与 Sorgenfrei函数。其中，Jaccard函数的形式为

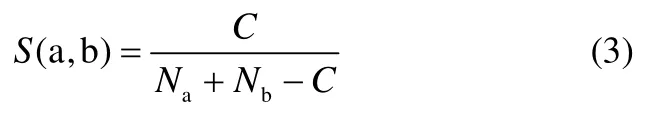
Sorgenfrei函数的形式为

式中，S为相似度大小，Na为序列a中出现的“1”的个数，Nb为序列b中出现的“1”的个数，C为两个序列中共同出现的“1”的个数。在Na、Nb不变的情况下，C的值越大，S的值越大，也就是说两个序列中同时出现的“1”越多，相似度越大。

为处理序列报警可能存在的整体延迟，可以对序列a进行时间长度为τ的整体平移，用平移得到的新序列aτ与b计算相似度S，并选取不同的τ多次计算以使S值最大，即

1.4 非规整报警相关性计算方法

利用传统的相似度函数可以计算有固定顺序形式的序列报警之间的相关性。但在实际生产过程中，还会出现延迟时间不固定和非对称的非规整报警，这类报警同样具有相关性，却是传统的方法无法挖掘到的。

因此，本文给出如下步骤计算非规整报警序列的相关性：

（1）计算序列a中“1”的数量，记为N；

（2）设定窗口长度l；

（3）对于序列a中的每一个“1”，若在序列b对应位置前后各为l的长度内存在一个“1”，则记为一个“A1”，将序列a中“A1”的数量记为m；

（4）则令序列b对序列a的相关性 /Sm N= ；

（5）同样的方法可计算序列 a对序列 b的相关性。

计算示例如图3所示，令l= 1。对于序列a，位置P1处的“1”在前后l的范围内不存在对应的“1”，而位置P2、P3处的“1”均可被记为“A1”，因此m=2 ，序列b对序列a的相关性S=2/3=0.66。

图3 相关性计算示例Fig.3 Example for correlation calculation

2 概率形式表示的相关性

2.1 概率形式表示相关性的基本思路

由相似度函数得到的报警相关性大小受到报警数量的影响，此外，报警限的高低也会影响报警相关性大小，这导致不同过程、不同位号，利用相似度函数计算出来的相关性并不具备可比性，难以确定一个固定的标准来比较两个报警序列的相关程度。

Yang等[11]指出，利用计算概率、不等式放缩与假设检验，可以得到传统相关性函数的相关性阈值，进而确定两个报警序列是否相关。但在使用非规整相关性计算方法后，序列a中一个位置的“1”是否记为“A1”不是单纯取决于序列b中的对应位置，而是取决于 b中对应位置前后各为l的长度内是否存在“1”，因此无法套用 Yang的方法计算阈值。为此，本文提出如下方法衡量相关性的大小：

（1）对于待测的两个序列a与b，记序列a中“A1”的个数为m；

（2）构造与待测序列中“1”的数量相同、但相互独立的序列a′与b′，由于这样的序列很多，因此记序列a′中存在的“A1”数量为随机变量X；

其中，最核心的部分为计算概率分布P(X=x)。

2.2 计算概率分布

令在序列a′中某一位置出现“1”的概率为ap′，序列b′中某一位置出现“1”的概率为bp′，并假设序列中各位置出现“1”的事件服从独立同分布。定义事件I为：如果序列a′中特定位置O出现“1”，且序列b′中位置 O前后各长度为l的窗口中出现“1”，则认为出现事件I，同时序列a′中的“1”可记为一个“A1”。

则事件I出现的概率p为

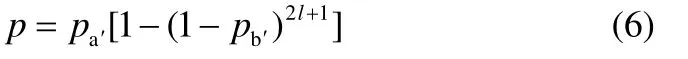
求解概率分布P(X=x)可以等价于计算事件 I发生的次数。在实际生产过程中，pa′、pb′均远小于1，即序列中“1”的个数极少，且l值往往较小，因此序列a′中多个位置的“1”对应于序列b′中同一个“1”的情况极为稀少，可以忽略。即认为事件I发生的概率服从独立同分布，X服从二项分布

式中，n表示序列的长度。

为验证式（7）的准确性，随机生成 10000对相互独立的0、1序列，序列长度均为2000，且有pa′=0.1，pb′= 0 .05，统计其中出现的 “A1”数量为k的序列对数量，并用此频率值与式（7）计算得到的概率值比对，结果如图4所示。

图4 概率分布结果验证Fig.4 Validation for result of probability distribution

可以看出，计算出的概率值与实际频率基本吻合。

在实际计算式（7）的过程中，可以用“1”出现的频率代替概率，即记序列长度为N，序列a′中“1”的个数为Na′，序列b′中“1”的个数为Nb′，则pa′=Na′/N，pb′=Nb′/N。

此外，可以仿照1.2节中介绍的ASCM图，采用概率形式代替传统计算方法得到的相关性，并将结果绘成色彩图，这样得到的图像更加具有可比性。

3 案例研究

3.1 仿真案例

假设i= 1 ,2,3,… ,1 00，而xA(i)是一个服从伯努利分布的随机变量xp(i)∈ ( 0,1)，且有P(xp(i)=0)= 0 .5，P(xp(i)= 1 )= 0 .5。对于t∈ [20i- 1 9,20i]，构造一对长度为2000的相关序列x(t)和y(t)

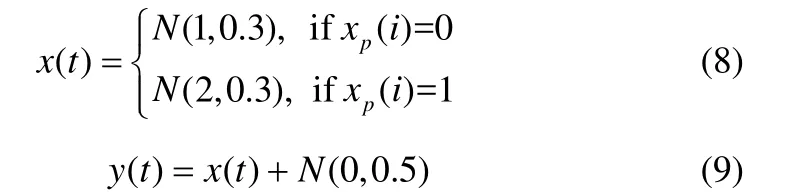
式中，N(μ,σ) 表示均值为μ、标准差为σ的正态分布。

为序列x(t)设置报警限2.5[图5 (a)]，y(t)设置报警限3.0[图5 (b)]，利用式（2）的方法得到报警序列xa1(t)与ya1(t)[图 5 (c)与图 5 (d)]，记为组 1#。将x(t)的报警限改为2.7，y(t)的报警限改为3.2，再次用式（2）的方法得到报警序列xa2(t)与ya2(t)，记为组2#。此外，利用Matlab生成长度为2000的随机0、1序列xa3(t)与ya3(t)，显然二者相互独立，如图6所示，记为组3#。分析这3组待测序列的相关性，得到结果如表1所示。

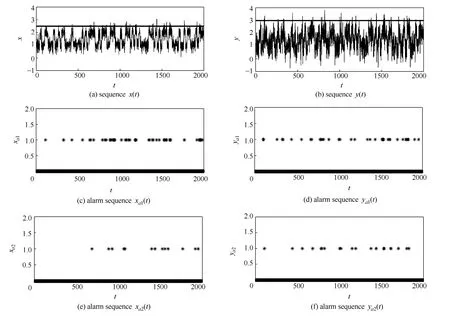
图5 仿真案例相关序列Fig.5 Dependent sequence of simulation case

图6 仿真案例独立序列Fig.6 Independent sequence of simulation case

表1 仿真数据的相关性分析Table 1 Correlation analysis of simulation data

对比组1#与组2#的结果可以看出，在报警限改变后，非概率形式的相关性由0.29降为0.14。而利用概率形式表示的相关性分别为0.99与0.85，说明即使报警限改变，但计算结果依然可以说明待测序列相关。

对比组2#与组3#中非概率形式表示的相关性，前者为0.14，后者为0.15，这与组3#为独立序列、组2#为相关序列的条件不符。这说明按照非概率形式，当报警限改变后，会出现相关序列计算出的相关性低于独立序列的情况。而在概率形式表示下，组3#的相关性仅有0.46，相比于组1#与组2#明显更低，是独立序列。这样的结果更符合实验条件。

需要说明，在利用概率形式表示相关性大小时，得到的结果会整体偏大，如独立序列组3#的相关性为0.46，远大于非概率形式时的0.15。而事实上，组3#利用概率形式表示的相关性大小为0.46，意味着待测序列3ax中“A1”数量大于独立序列3ax′中“A1”数量这一事件发生概率仅有46%，显然不能说明待测序列3ax与3ay相关。

3.2 工业案例

选取国内某化工厂聚合装置作为分析对象，局部流程如图7所示。以E釜为例，聚合釜R21E进料包括反应用水REC-WAT、引发剂INI，单体VCM经由泵P52A打入储罐R52，再经由阀V28进入聚合釜。冷却水COLD-WAT由泵P21E打入夹套，机封水SEAL-WAT进入釜底的搅拌机。聚合釜出料为气相产物GAS与产品PRODUCT。

图7 聚合工艺局部流程Fig.7 Scheme for part of polymerize process

选取该装置中时间跨度为1个星期内报警最多的15个位号进行统计，利用传统相关性计算方法得到ASCM图，如图8所示。做出使用非规整报警相关性计算方法并使用概率形式表示的色彩图，如图9所示。

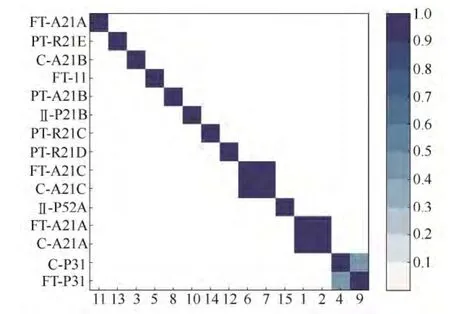
图8 传统方法得到的ASCM图Fig.8 Alarm similarity color map made by traditional method

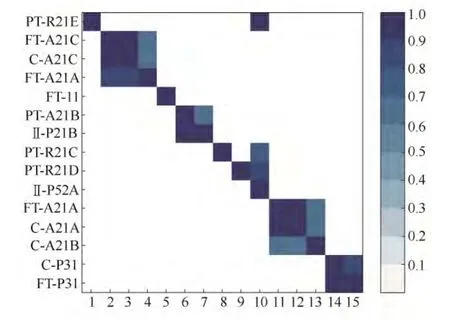
图9 利用非规整报警相关性计算方法且用概率形式表示的色彩图Fig.9 Color map made by non-regular alarm correlation method in form of probability

可以看出，传统的ASCM图仅得到3组相关位点，分别为 FT-A21C与 C-A21C、FT-A21A与C-A21A、C-P31与FT-P31。这3组位点都为序列报警，且都是管路流量与该管路阀门阀位，其相关性显而易见，因此指导意义有限。

而利用非规整报警相关性计算方法且用概率形式表示的色彩图还可以得到以下3组相关位点。

（1）位点II-P52A对位点PT-R21E、PT-R21C、PT-R21D分别呈现出相关性。II-P52A为聚合釜单体进料泵的电流，而PT-R21E、PT-R21C、PT-R21D分别为3台聚合釜的压力。聚合釜单体进料增加会导致反应加剧，进而引发聚合釜的压力升高，因此该相关性成立。而 PT-R21E、PT-R21C、PT-R21D对II-P52A的相关性并不成立，所以此组相关位点属于非对称的相关位点。

（2）位点PT-A21B与II-P21B互相呈现出相关性。II-P21B为聚合釜B的循环水泵电流，PT-A21B为聚合釜B的搅拌机封水压力。聚合釜循环水泵加大功率后，会导致循环水流量上升，聚合釜温度下降，聚合釜内以及与聚合釜联通的机封水管路压力均下降，因此该相关性成立。当釜内反应物的存量变化时，报警循环水泵功率过大与报警釜内压力过低发生的间隔时间也会变化，所以此组相关位点属于延迟时间变化的相关位点。

（3）不同釜之间搅拌机封水流量（如FT-A21A与FT-A21C）之间呈现出相关性。由于各分管路间的搅拌机封水流量由同一个总阀门控制，因此分管路间的搅拌机封水流量会同时波动，该相关性成立。当总管路与各分管路的流量变化时，某两个分管路间搅拌机封水流量报警发生的间隔也会发生变化，所以此组相关位点属于延迟时间变化的相关位点。

可以看出，利用非规整报警相关性计算方法且用概率形式表示的色彩图可以得到更加全面、准确的结果。此外，上述15个位号中存在3组相关的非规整报警与3组相关的序列报警，相关的非规整报警组数占到全部相关组数的50%，这说明非规整报警相关性应该得到足够的重视。

需要说明，聚合装置的操作参数需要随着产品牌号的不同而进行改变，而操作参数的改变必然会影响各位点的报警序列，进而影响到挖掘出的相关性结果。与此类似，当化工装置的生产工况发生改变时，需要重新进行相关性挖掘。

为了进一步说明不同方法之间存在的差异，选取位点II-P52A与PT-R21D为待测序列组1，位点II-P21B与PT-A21B为组2，位点FT-A21C与C-21C为组3，C-A21B与II-P52A为组4，分别利用传统的 Jaccard相关性函数、非规整报警相关性计算方法、概率形式表示的相关性大小进行分析。其中，组1为非对称的相关位点，组2为延迟时间不固定的相关位点，组3为相关的序列报警位点，组4为相互独立的对照组。在利用非规整报警相关性计算方法与概率形式时，仅分析每组两个位点中前者对后者的相关性，如组2中即为II-P52A对PT-R21D的相关性。

此外，可以进一步计算组 1中 PT-R21D对II-P52A的相关性，得到利用概率形式表示的相关性大小为0.56。因此，PT-R21D对II-P52A的相关性不成立，这与组1为非对称相关位点的条件一致。

由表2可以看出，非规整报警相关性计算方法与传统相关性函数相比，可以更好地挖掘出延迟时间变化（组1）、非对称（组2）的相关性位点。然而，仅利用非规整报警相关性计算方法而不使用概率形式表示时，组1与组4的结果十分接近，这与组1相关、组4独立的条件不符。相比之下，利用概率形式表示的相关性结果更加合理。

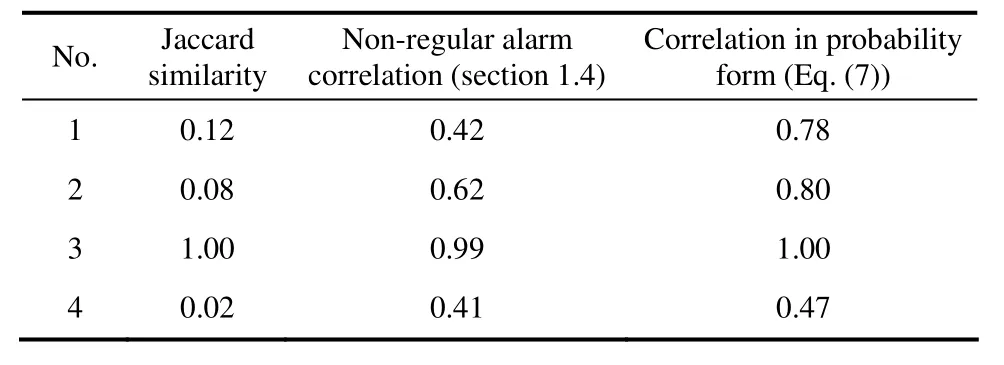
表2 实际数据的相关性分析Table 2 Correlation analysis of industry data

4 结 论

本文在传统的基于凝聚层次聚类的报警相关性发掘算法基础上，对相关性计算方法进行改进，提出了非规整报警相关性计算方法，从而能够更全面、更准确地挖掘化工过程中不同变量间的相关性。经由工业数据验证，改进后的相关性发掘算法能够挖掘出延迟时间变化、非对称的相关位点，得到真实存在而传统算法很难发掘到的相关性。

此外，本文提出了利用概率形式表示相关性大小的计算方法，使不同位号、不同装置间的相关性大小具有可比性，这在3.2节的工业案例中得到了验证。在报警相关性发掘算法中，一个重要的问题是当变量的报警限改变、报警数量大幅变化后，如何保证发掘相关性的算法结果依然成立。经过 3.1节中数据的验证，利用概率形式表示相关性大小的方法可以有效解决此问题。

[1] Izadi I, Shah S L, Shook D S, Chen Tongwen. An introduction to alarm analysis and design//The 7th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes [C].Barcelona, 2009.

[2] Engineering Equipment and Materials Users’ Association (EEMUA).EEMUA Publication 191：alarm systems—a guide to design,management and procurement [S]. London, 2007.

[3] Rothenberg D H. Alarm Management for Process Control：A Best-Practice Guide for Design, Implementation, and Use of Industrial Alarm System [M]. NewYork：Momentum Press, 2009.

[4] Izadi I, Shah S L, Shook D S, Kondaveeti S R, Chen Tongwen. A framework for optimal design of alarm systems//The 7th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes [C]. Barcelona, 2009.

[5] Zhao Jinsong (赵劲松), Zhu Jianfeng (朱剑锋). Data filtering based alarm processing strategy for repeating alarms [J].Journal of Tsinghua University：Science and Technology(清华大学学报：自然科学版), 2012, 52 (3)：277-281.

[6] Zhu Jianfeng, Shu Yidan, Zhao Jinsong, Yang Fan. A dynamic alarm management strategy for chemical process transitions [J].Journal of Loss Prevention in the Process Industries, 2014, 30：207-218.

[7] Choi Seung-Seok, Cha Sung-Hyuk, Tappert C C. A survey of binary similarity and distance measures [J].Journal of Systemics,Cybernetics and Informatics, 2010, 8 (1)：43-48.

[8] Kondaveetia S R, Izadi I, Shaha S L, Black T, Chen Tongwen.Graphical tools for routine assessment of industrial alarm systems [J].Computers & Chemical Engineering, 2012, 46：39-47.

[9] Ahmed K, Izadi I, Chen Tongwen, Joe D, Burton T. Similarity analysis of industrial alarm flood data [J].Automation Science and Engineering,IEEE Transactions on, 2013, 10 (2)：452-457.

[10] Yang F, Shah S L, Xiao D, Chen T. Improved correlation analysis and visualization of industrial alarm data [J].ISA Transactions, 2012, 51(4)：499-506.

[11] Yang Zijiang, Wang Jiandong, Chen Tongwen. Detection of correlated alarms based on similarity coefficients of binary data [J].Automation Science and Engineering, IEEE Transactions on, 2013, 10 (4)：1014-1025.

[12] Faith D P. Asymmetric binary similarity measures [J].Oecologia,1983, 57 (3)：287-290.

[13] Masaru N, Fumitaka H, Tsutomu T, Hirokazu N. Event correlation analysis for alarm system rationalization [J].Asia-Pacific Journal of Chemical Engineering, 2011, 6 (3)：497-502.

[14] Johnson S C. Hierarchical clustering schemes [J].Psychometrika,1967, 32 (3)：241-254.