模态试验传感器优化布置的松弛序列法*

潘 安，彭珍瑞，殷 红，董海棠

(兰州交通大学 机电工程学院，甘肃 兰州730070)

0 引 言

模态分析是结构动力学分析的基础，其中模态试验是模态分析的一种常用方法。模态试验系统中传感器布置直接影响了试验效果［1］。如何将传感器以最少的数目布置在最佳的位置是模态试验传感器优化布置问题的目的。

解决传感器优化布置问题，首先要根据试验目标的不同确定优化准则，然后选择适当的优化方法。常用的布置准则有:Kammer D C 提出的有效独立法［2］;Carne T G 和Dohrmann C R 根据模态保证准则(modal assurance criterion，MAC)提出以MAC 矩阵最大非对角元素为目标函数的优化准则［3］。传感器配置的优化方法分为传统方法和随机类算法。随机类算法如模拟退火［4］、遗传算法［5］等;传统方法中基于MAC 法提出的序列法(逐步积累法［6］、逐步消去法［7］)最为实用，应用广泛［8］。

松弛思想源于图论中的最短路径问题［9］。松弛操作被Dijkstra 算法、有向无环图最短路径算法和Bellman－Ford算法使用，成功地在多项式时间复杂度内求出了最短路径问题的最优解。

在序列法的基础上，通过融入松弛思想，本文提出松弛序列法。松弛序列法首先执行积累序列法得到不同传感器数量对应的初始布置方案，然后对每个初始布置方案进行松弛操作。

1 基于松弛序列法的传感器优化布置

1.1 理论基础与优化准则

结构动力学中，n 自由度系统的运动方程可以表示为

其中，M，C，K，f(t)和x(t)分别表示质量矩阵、阻尼矩阵、刚度矩阵、力向量和响应向量。根据模态叠加性原理，响应向量可以表示为

其中，Φ 为模态振型矩阵，q(t)为模态坐标向量。

实践上，模态试验工程师需要观察模态振型，通过视觉判断模态的精度。Carne T G 和Dohrmann C R 根据MAC提出的无关性度量公式符合模态试验工程师需要观察模态振型的视觉要求［3］。MAC 矩阵i 行j 列的元素计算公式为

其中，Φi和Φj分别为Φ 的第i 列和第j 列，Φ 为布放方案的振型矩阵。

将振型矩阵^Φ 中第k 行(此行还未被Φ 选取)加到现有布放方案中去，MAC 就变为［3］

其中，A=ΦTΦ 为已有布置方案的振型矩阵的乘积，为的第k 行i 列的元素为完整的振型矩阵。

1.2 积累序列法

序列法的基本思想是每次从剩余的候选布放位置中选择最优的一个加入现有解，直至目标函数达到设定条件。QR 分解用于确定初始布置方案。设n 自由度结构的前m阶振型矩阵为，则其中，E ∈Rn×n为 置 换 矩 阵，Q ∈Rm×m，R ∈Rm×n，

|R11|＞|R22|＞…＞|Rmm|。

1.3 松弛思想

松弛思想是在原有估计的基础上，通过增广现有解得到新解当增广解优于现有的解时，原有估计将被更新。传感器优化布置的松弛序列法采用以最优方式增加和减小布放传感器的方式，执行松弛操作。同时，采用式(4)评价增广解，可以降低操作的时间复杂度。

1.4 松弛序列法

松弛序列法将松弛思想引入传感器优化布置的积累序列法中，算法的流程如图1 所示。

图1 算法的流程图Fig 1 Flow chart of algorithm

传感器优化布置的松弛序列算法的执行过程分为以下步骤:

1)根据1.2 节描述的积累序列法，得到初始布置方案集合。

2)遍历当前布置方案集合，执行松弛操作。例如:对于含有t 只传感器的布置方案，计算其增加一只传感器和减小一只传感器后产生的两个新布置方案(得到含有t－1 只传感器的新布置方案和含有t+1 只传感器的新布置方案)，如果新布置方案优于对应传感器数量的原有布置方案，则用新布置方案替换原有布置方案(松弛成功);否则，保留原有布置方案(松弛失败)。

3)如果步骤(2)中产生了松弛过程(即其中的某个解被松弛成功)，返回步骤(2)继续执行;反之，结束计算，输出结果。

2 算 例

以图2 所示的悬索桥的加速度传感器优化配置为例，实施传感器优化配置问题的松弛序列法。某悬索桥［10］采用钢筋混凝土加劲桁架悬索桥体系，索塔中心间距为128 m，高54 m。桥面宽度为10.8 m，长度220 m。利用ANSYS 14.0建立悬索桥的有限元模型。对建立的悬索桥有限元模型进行模态分析，提取桥面的两侧214 个节点的y 轴和z 轴方向(共428 个自由度)的前9 阶振型，得到振型矩阵Φ∈R428×9。以Matlab R2010a 为平台，进行数值模拟。

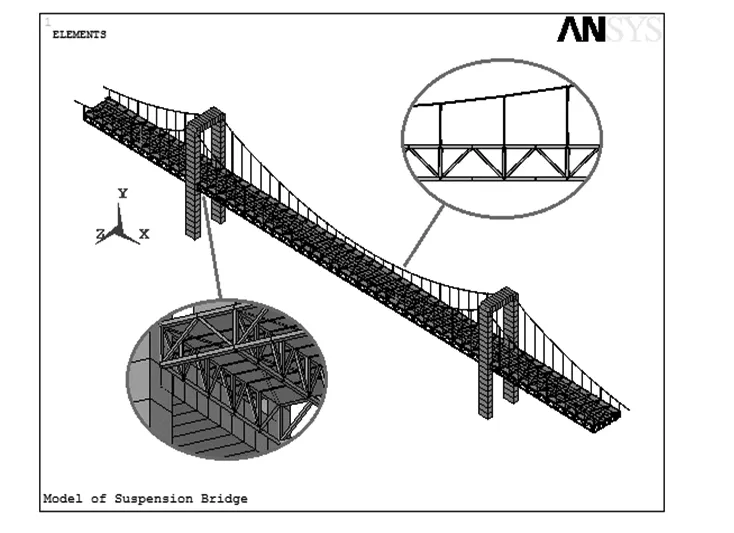
图2 悬索桥的有限元模型Fig 2 Finite element model of suspension bridge

分别采用积累序列法和松弛序列法(本文方法)进行优化配置，对比结果如图3 所示。从图3 中曲线可以看出，松弛序列法的布置效果明显优于积累序列法的布置效果。当传感器数量相同时，松弛序列法和积累序列法的布置结果对比如表1 所示，松弛序列法的MAC 矩阵最大非对角元素值较小，表明在模态相似性方面优于松弛序列法。当目标函数取值相同时，松弛序列法和积累序列法的布置结果对比如表2 所示，表明在模态相似性要求相同时，松弛序列法需要的传感器个数较少，有效减小了实验成本。

图3 积累序列法与松弛序列法的结果对比图Fig 3 Results comparison of two algorithms

表1 传感器数量相同时，两种方法的布置结果对比Tab 1 Placement results comparison of two algorithms when numbers of sensors are the same

表2 目标函数取值相同时，两种方法的布置结果对比Tab 2 Placement results comparison of two algorithms when target functions are the same

从图3 中松弛序列法的曲线可以看出，当选择的传感器只数为25 时，MAC 矩阵最大非对角元素就已经达到很好的优化效果，继续增加传感器时曲线下降缓慢。因此，本文最终选择25 只传感器，作为悬索桥模态试验的最终配置，此时MAC 矩阵最大非对角元素0.028 59。图4 和图5分别显示了积累序列法和松弛序列法得到的MAC 矩阵，其中第2 阶模态和第7 阶模态相似度最高，图4 和图5 中分别为0.061 56和0.028 59，可见两种方法中松弛序列法的优化布置方案较好。

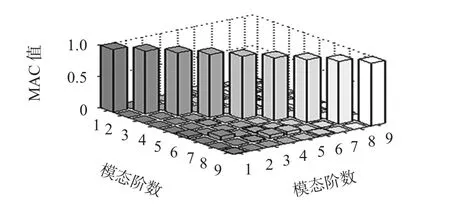
图4 积累序列法布置25 只传感器的MAC 柱状图Fig 4 MAC histogram of 25 sensors placed by accumulation sequential algorithm

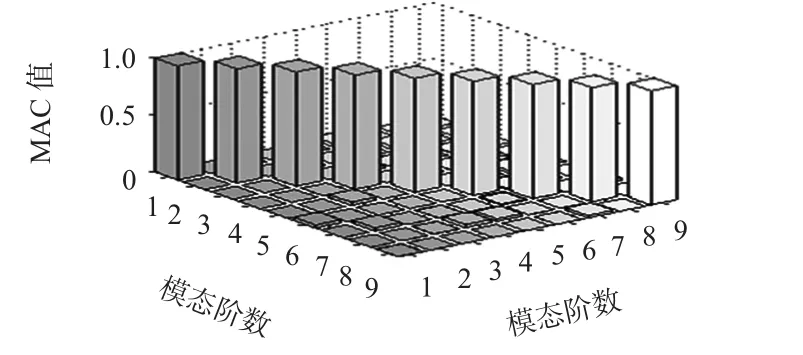
图5 松弛序列法布置25 只传感器的MAC 柱状图Fig 5 MAC histogram of 25 sensors placed by sequential algorithm with relaxation

3 结束语

本文将松弛思想应用于模态试验传感器优化布置问题中，松弛序列法在积累序列法的基础上，使MAC 矩阵的最大非对角元素进一步降低。当布置的传感器数量相同时，由于布置的传感器位置不同，与积累序列法相比松弛序列法得到的振型相似性更低，便于模态试验者观察振型;当振型相似性的标准一致时，与积累序列法相比松弛序列法需要的传感器数量更少，不仅可以节约模态试验的成本，而且能够减少数据采集、数据传输和数据分析的工作量。

［1］ 海伦·W，拉门兹·S，萨斯·P.模态分析理论与试验［M］.白化同，郭继忠，译.北京:北京理工大学出版社，2001:118－121.

［2］ Kammer D C.Sensor placement for on－orbit modal identification and correlation of large space structures［J］.Journal of Guidance，Control，and Dynamics，1991，14(2):251－259.

［3］ Carne T G，Dohrmann C R.A modal test design strategy for model correlation［C］∥Proceedings of the 13th International Modal Analysis Conference，1995:927－927.

［4］ 田 莉，陈换过，祝 俊，等.基于自适应模拟退火遗传算法的传感器优化配置研究［J］.振动工程学报，2012，25(3):238－243.

［5］ 耿 飞，龙海辉，赵健康，等.基于改进遗传算法的传感器优化配置［J］.计算机仿真，2014，31(5):56－59.

［6］ 秦仙蓉，张令弥.一种基QR 分解的逐步累积法传感器配置［J］.振动、测试与诊断，2001，21(3):168－173.

［7］ 黄民水，朱宏平，宋金强.传感器优化布置在桥梁结构模态参数测试中的应用［J］.公路交通科技，2008，25(2):85－88.

［8］ 梁 鹏，李 斌，王晓光，等.基于桥梁健康监测的传感器优化布置研究现状与发展趋势［J］.建筑科学与工程学报，2014，31(1):120－129.

［9］ Cormen T H，Leiserson C E，Rivest R L，et al.Introduction to algorithms［M］.3rd ed.Cambridge:MIT Press，2009:648－650.

［10］包 陈，王呼佳，陈洪军，等.ANSYS 工程分析进阶实例［M］.修订版.北京:中国水利水电出版社，2009:183－206.