框架式垂直陀螺仪误差特性研究

李丽锦，汤恒先，周志广，周军涛

(西北工业大学 第365 研究所，陕西 西安710065)

0 引 言

框架式垂直陀螺仪是测量飞机姿态角(俯仰角和倾斜角)的一种装置，是飞机自动驾驶仪的主要部件之一，并具有“仪表之王”的美称，在军事和民用领域广泛应用［1］。近代飞机以框架式垂直陀螺仪为敏感元件组成飞机的姿态系统，并形成中心姿态信号源，使框架式垂直陀螺仪仍具有不可取代的地位［2］。

框架式垂直陀螺仪主要由双自由度陀螺仪、修正装置组成，其工作原理是基于综合利用了陀螺和摆的特性。陀螺自转轴具有方向的稳定性，但缺少方向的选择性;摆对地垂线具有方向的选择性，但缺少方向的稳定性。框架式垂直陀螺仪结构特性使其测量具有完全自主、可靠性高等特点，但也使其在运动状态下具有原理性测量误差。

本文针对框架式垂直陀螺的结构特性，推导出其在运动状态下的误差模型，并进行仿真和实验验证，为工程应用提高测量精度提供了理论基础。

1 框架式垂直陀螺仪运动方程

根据框架式垂直陀螺仪的结构特点和动静分析法，其运动方程如下［3］

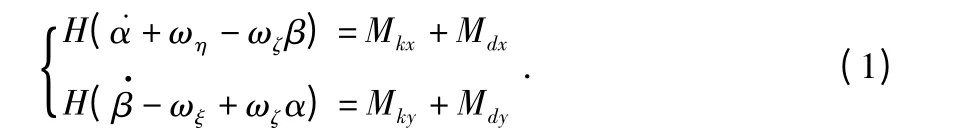
其中，H 为垂直陀螺的角动量;α 为内环横轴与地平横轴夹角(影响倾斜角)，β 为内环纵轴与地平纵轴夹角(影响俯仰角)，实际上就代表了自转轴相对地垂线的运动;Mkx，Mdx分别为作用在内环上的修正外力矩和干扰外力矩;Mky，Mdy分别为作用在外环上的修正外力矩和干扰外力矩;ωη，ωξ，ωζ分别为倾斜角速率，俯仰角速率，航向角速率。

2 机体静止状态分析

当机体处于静止状态，ωη，ωξ，ωζ均为零，运动方程式(1)可简化为

在断开陀螺修正情况下，即Mkx=Mky=0，假设自转轴初始偏角为α0，β0，可得运动规律如下

由式(3)可知，在静止状态下，在断开陀螺修正情况下，框架式垂直陀螺仪测量值随时间呈线性变化关系。

3 机体水平加速运动分析

设飞机作水平加速飞行，纵向加速度为a，则作用在摆上的惯性力使沿纵轴偏离地垂线，处于视垂线位置，该横向偏角为

这时纵修正装置将产生错误的修正力矩，使自转轴向视垂线进动而沿横向偏离地垂线，从而造成俯仰角的测量误差。

以常值式修正为例，在常值式修正中，修正力矩的大小为一常值，与自转轴偏角的大小无关，而其符号则取决于偏离的方向，作用在内、外环轴上的修正力矩表达式为

式中 Mkx和Mky为常值修正力矩的量值;而sgn 为表示符号正或负的函数，sgn α 的定义为

sgn β 的定义与此相同。

从运动方程分析，在纵向错误的常值修正力矩作用下，假设陀螺干扰力矩为零，ωη，ωξ，ωζ均为零。运动方程式(1)可简化为

自转轴向视垂线的进动偏角即为陀螺的加速度误差

其中，ta为飞机连续加速时间。

由式(8)可看出，由于飞机水平加速所引起的框架式垂直陀螺仪俯仰角测量误差与时间呈正比。如果加速的时间较长，则自转轴有可能被错误修正到视垂线位置，这时测量误差的最大值即为θa。例如:假设纵向修正速度为2°/min，则机体连续加速1 min 时，错误的纵向修正产生的测量误差为2°。

因此，在加速度时间比较长，纵向加速度值比较大的情况下，飞机大多采用切断框架式垂直陀螺仪的纵向修正来减小该项误差。

4 机体盘旋运动分析

设飞机作盘旋飞行，盘旋角速度为ωζ，则沿横向必存在向心加速度ωζV，从而存在向心力［4］，这时框架式垂直陀螺仪的摆受到重力和向心力的合力作用，沿横向偏离地垂线，处于视垂线位置，该横向偏角为

这时横向修正装置将产生错误的修正力矩，使自转轴向视垂线进动而沿横向偏离地垂线［5］，从而造成倾斜角的测量误差。而且，由于飞机盘旋角速度的影响，还将引起自转轴沿纵向偏离地垂线，从而造成俯仰角的测量误差。

从运动方程分析，由于飞机在盘旋时，俯仰角速度和倾斜角速度几乎为零，假设ωη，ωξ为零。运动方程(1)可简化为

求取微分方程式(10)的解析解

其中

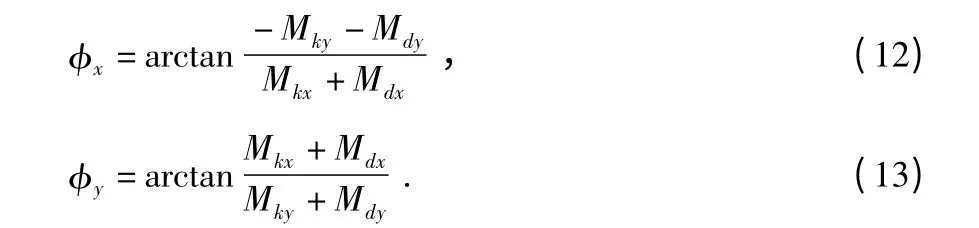
由式(11)可看出，由于飞机盘旋在框架式垂直陀螺仪俯仰角和倾斜角方向均会引起测量误差，该测量误差与修正速度呈正比，与盘旋角速度呈反比，且呈正弦变化。

由于在实际应用中，框架式垂直陀螺仪内环和外环均存在干扰力矩［6］，即使将横向修正和纵向修正力矩均断开，框架式垂直陀螺仪在盘旋状态下的俯仰角和倾斜角测量误差均呈正弦变化。目前，在盘旋状态下，飞机大多采用切断框架式垂直陀螺仪的横向修正来减小盘旋误差［7］。

5 仿真与实验结果

5.1 仿真结果

假设陀螺角动量4 000 gf·cm/s，纵向摩擦力矩4 gf·cm，横向摩擦力矩4 gf·cm;纵向修正力矩8 gf·cm，横向修正力矩8 gf·cm。

1)15°右盘盘旋角速率ωζ=2.55°/s 情况下，接通与断开横向修正的倾斜角仿真结果分别如图1、图2 所示。

2)25°右盘盘旋角速率ωζ=5.6°/s 情况下，接通与断开横向修正的倾斜角仿真结果分别如图3、图4 所示。

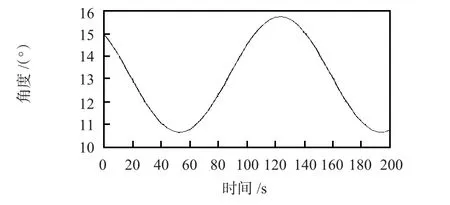
图1 横向修正下的倾斜角仿真结果Fig 1 Simulation results of inclination angle under lateral correction

图2 无横向修正的倾斜角仿真结果Fig 2 Simulation results of inclination angle without lateral correction

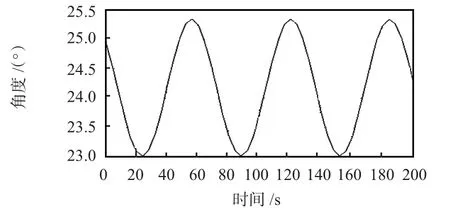
图3 横向修正下的倾斜角仿真结果Fig 3 Simulation results of inclination angle under lateral correction

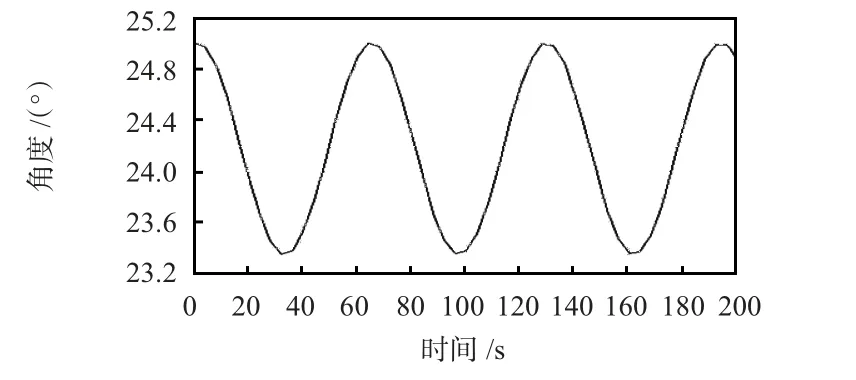
图4 无横向修正的倾斜角仿真结果Fig 4 Simulation results of inclination angle without lateral correction

5.2 实验结果

以某型框架式垂直陀螺仪模拟盘旋状态做跑车试验。将框架式垂直陀螺仪分别倾斜15°和25°固定于车内，并分别以角速率ωζ=2.55°/s 和ωζ=5.6°/s 进行试验。由于实际应用中盘旋状态下自动断开横向修正，仅以断开横向修正的倾斜角为例，得出实验结果如图5、图6 所示。

仿真和试验结果表明:

1)框架式垂直陀螺仪在盘旋状态下测量误差呈周期性变化，其变化周期与盘旋周期一致;

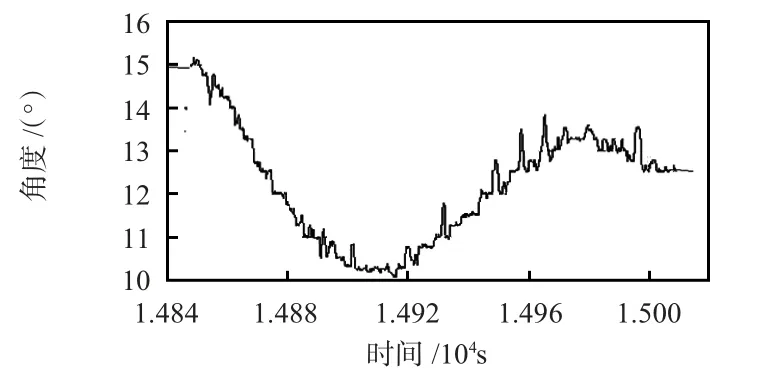
图5 ωζ=2.55°/s 下的倾斜角试验结果Fig 5 Experimental results of inclination angle when ωζ=2.55°/s

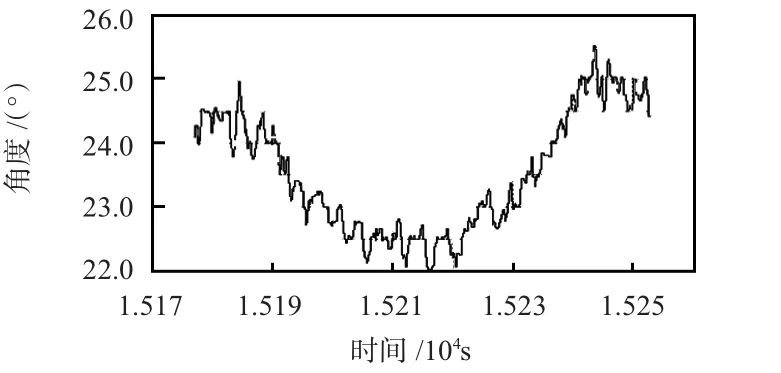
图6 ωζ=5.6°/s 下的倾斜角试验结果Fig 6 Experimental results of inclination angle when ωζ=5.6°/s

2)框架式垂直陀螺仪在盘旋状态下测量误差幅值与修正力矩呈正比。

6 结束语

本文着眼于框架式垂直陀螺仪的测量误差研究，针对在工程不同状态下实际应用情况，对其结构运动特性进行数学解析分析，同时推导出具有工程意义的原理性误差特性，为工程应用提供了理论基础，同时，在此基础上进行误差建模与模型仿真，并进行试验验证。这对于航空工程应用中尤其是余度控制误差研究乃至保障飞行安全与任务作业精度有着重要的意义。

［1］ 冯 莉，董桂梅.陀螺灵敏部的精密升降定位控制［J］.传感器与微系统，2010，29(4):114－116.

［2］ 董桂梅，赵东升.陀螺经纬仪全自动化关键技术的研究［J］.传感器与微系统，2010，29(3):29－31.

［3］ 王有隆.航空仪表［M］.成都:西南交通大学出版社，2001.

［4］ Race R，Schott C，Huber S.Electronic compass sensor［C］∥Proceeding of IEEE，2004:1446－1449.

［5］ 林玉池，林明春，夏桂锁，等.全自动智能陀螺寻北仪中待测光标信号采集模块的设计［J］.传感器与微系统，2007，20(3):559－562.

［6］ 郭金运，刘 新，李瑞国.陀螺经纬仪陀螺定向测量分析［J］.山东矿业学院学报，1998，17(4):323－328.

［7］ Vaneck T W.Fuzzy guidance controller for an autonomous boat［J］.IEEE Control Systems Magazine，1997，17(2):43－51.