一种基于改进支持度的节能型WSNs 数据融合算法*

王 波，孙智国，熊 涛

(重庆大学 计算机学院，重庆400044)

0 引 言

无线传感器网络(WSNs)应用数据融合技术可将来自多个节点的数据进行整合，降低网络的能耗、提高数据采集的准确性和效率［1］。但由于节点自身的测量误差、部署环境、传输误差等因素的影响，节点采集到的数据往往含有不确定或错误的信息，并不能完全反映事物的真实情况，因此，在数据融合时需要找出不同数据间的关系来确定其可信度，并根据数据的可信度进行融合［2］。支持度函数的数据融合方法可以很好地完成这一任务，引起了广泛的研究兴趣。文献［3］提出一种指数衰减函数计算传感器数据间的支持度，并通过多次实验确定了数据一致性度量最优的计算方式。文献［4，5］运用指数衰减函数计算传感器数据间的支持度，提出了一种充分利用数据一致性度量蕴含的可信度的加权方式进行数据融合。文献［6］针对时变非线性的状态估计问题提出了一种置信距离的支持度函数，使用该函数进行多传感器的数据融合。文献［7］对基于置信距离的支持度函数的支持度函数进行了调整，并与加权数据融合算法相结合用于雷达的目标识别中。文献［8］提出基于邻近量测认知信息的支持度函数获得传感器数据的一致性关联矩阵，用于多传感器的数据融合进行温度检测。

支持度函数的数据融合算法运行于汇聚节点，依次接收感知节点发送的每一个数据进行融合，这种方法不利于节省节点能量。本文在感知节点对数据进行初次融合，并将自支持度的概念与灰色接近度理论相结合的改进支持度函数数据融合算法用于汇聚节点，提出一种节能型WSNs数据融合算法。通过仿真实验表明:该算法在提高数据融合的精确度的同时，还可以降低节点的能耗。

1 基于改进支持度的节能型WSNs 数据融合过程

本文提出的基于改进支持度的节能型WSNs 数据融合算法包括感知节点监测数据的初次融合和汇聚节点的二次数据融合两部分，其融合模型如图1 所示。在感知节点依据设定的阈值对采集到的数据进行初次融合并传送给汇聚节点;汇聚节点收到初次融合的数据后，采用改进支持度函数计算最终的融合估计值。

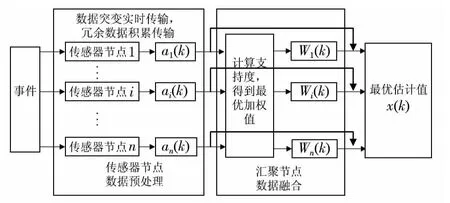
图1 数据融合模型Fig 1 Data fusion model

2 感知节点监测数据的初次融合过程

感知节点监测数据初次融合的目的主要是减少节点间的数据通信量、降低节点能耗。由文献［9］可知，计算上的能耗是通信能耗的10－3倍，因此，在感知节点对数据进行初次融合，减少数据的通信量是可达到节能的目的。假设WSNs 中:1)由n 个传感器节点监测同一环境;2)传感器被唤醒后以等待时间间隔t 采集一次数据为aij(i=1，2，…n;j=1，2…)。

设定2 个阈值δ 和τ，其中，δ 取传感器的最大误差，用来限定节点采集到的数据间的最大差值，τ 用来限定采集次数，每个传感器将采集的数据保存在节点存储器中。数据的预处理分为两种情况［10］:1)如果第i(i ＜τ)次采集到的数据与前i－1 次采集到的数据任意一个之间的差值超过阈值δ 时，此时认为数据出现突变，计算前i－1 次数据的均值并发送到汇聚节点。2)当采集数据的次数达到τ 次时，计算前τ－1 次数据的均值并发送到汇聚节点，将第τ 次的数据作为下一次采集的第一个数据。

节点采集到的数据的预处理过程如下:

1)设ai1为第i 个节点采集的第1 个数据。

2)每采集一次数据aij，分别与前j－1 次的数据ai1，ai2，…，aij－1进行比较:

a.当任一组数据的差值超过阈值δ，即|aij－aik|＞δ，k=1，2，…，j－1 时，认为数据出现突变，计算前j－1 次采集到数据的均值

b.当数据的采集次数超过τ 时，计算前τ－1 次采集到数据的均值

3)将第j 次采集的数据aij作为下一次采集的第一个数据ai1，将¯a 发送到汇聚节点。

4)重复步骤(1)～(3)。

3 基于改进支持度函数的汇聚节点数据融合算法

经过传感器感知节点初次融合后的数据和实际值之间仍可能存在较大的误差，需要对初次融合值进行再次融合。

用指数衰减型支持度函数描述传感器节点数据间的支持度，其定义如下:

定义1 d=exp(－β(a－b)2)。其中，参数β 是支持度衰减因子，对于指定的|a－b|，调整β 的大小，可以调整支持度函数的衰减幅度。

3.1 改进型支持度函数的一致性度量算法

为了更可靠地评估不同传感器节点数据间的支持度，除了要考虑同一时刻，不同传感器节点数据的可靠性，还应该考虑同一节点在整个观测区间内多次采集到数据的可靠性，据此本文提出一种改进的支持度函数。

设k(1≤k≤m)时刻传感器节点i，j 经预处理后的数据分别是ai(k)和aj(k)。

定义2 传感器节点i 的自支持度为

由改进支持度函数的定义可知:

1)zij(k)=zji(k)，即传感器节点i，j 的数据对彼此的支持度是相同的。

2)zij(k)的取值范围为0≤zij(k)≤1;当zij(k)=0 时，表示传感器节点i，j 的数据互不支持;当zij(k)=1 时，表明传感器节点i，j 的数据强支持。

由改进支持度函数计算出各传感器节点数据的支持度并构建支持度矩阵

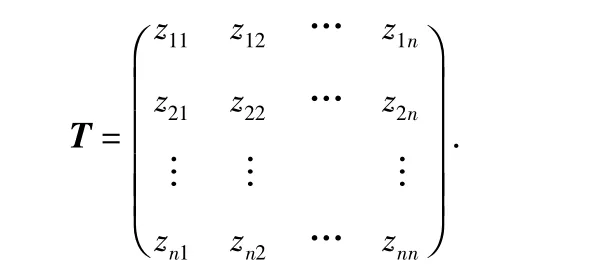
在k 时刻，传感器节点i 的数据与其他所有传感器节点数据的一致性度量为

0≤γi(k)≤1，传感器节点数据的支持度一致性度量反映了在某个观测时刻，第i 个传感器节点数据与其他传感器节点数据的接近程度，若γi(k)大，表明k 时刻第i 个传感器节点数据与其他传感器节点数据的接近度高;反之，第i 个传感器节点数据偏离多数传感器节点数据。

3.2 使用改进支持度函数计算汇聚节点的融合估计值

为保证事件发生的整个观测区间上一致性和可靠性高的传感器节点数据充分被利用，采用传感器节点数据的一致性均值和一致性方差的概念来描述事件发生的整个观测区间上各个传感器节点数据一致性度量蕴含的可靠性［4］。

整个观测区间上的m 个观测时刻，第i 个传感器节点数据的一致性均值为

第i 个传感器节点数据的一致性方差为

为充分利用一致性均值大，且一致性方差小的传感器节点数据，取第i 个传感器节点数据的加权值wi与数据一致性均值正相关，而与数据一致性方差负相关

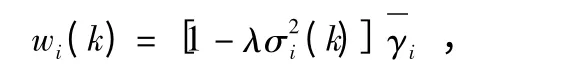
融合后的最优估计值为

式中 ai(k)为k 时刻传感器节点i 的数据，wi(k)为时刻传感器节点i 的数据的加权值。

4 仿真实验与结果分析

采用Matlab 7.0 进行仿真测试，模拟出一个温度保持在900 ℃左右的恒温箱内部环境，3 个节点随机的散布在恒温箱内部，以相同的时间间隔采集一次温度数据，每个节点的初始能量为2 J。文献［4］中采用3 个传感器节点对恒温箱进行温度检测得到了6 组观测数据如表1 所示，为尽可能地使模拟测试的数据接近真实情况，本测试使用这组数据作为原始数据。

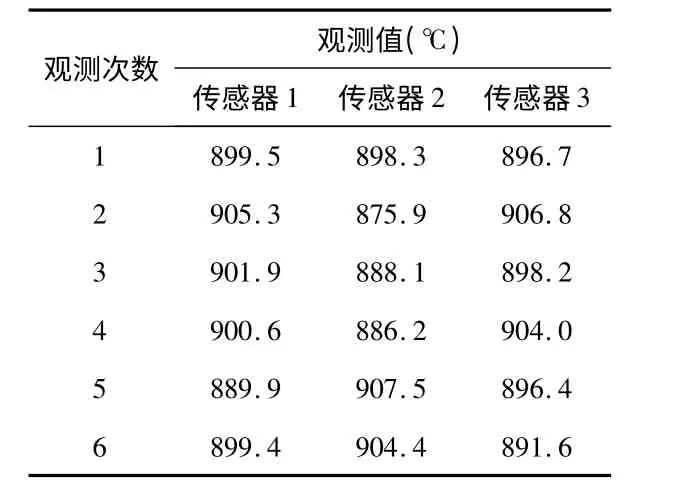
表1 传感器节点的观测数据Tab 1 Observed data of sensor nodes

4.1 融合结果分析

以加权数据融合作为算法1，以文献［3］中的指数衰减型支持度函数进行数据融合的方法作为算法2，以文献［8］中基于邻近量测认知信息的支持度函数进行数据融合的方法作为算法3，与本文算法对表1 数据融合后的结果如表2所示，为详细比较四种方法的融合效果，将数据采集的次数提高到100 次，得到的绝对误差效果如图2 所示。

从图2 和表2 的实验结果可以看出:加权数据融合算法因需人为设置传感器的方差，其融合精度最低;本文算法的绝对误差最小约为0.98 ℃，更加接近真实值(900 ℃)。

表2 融合结果Tab 2 Fusion results

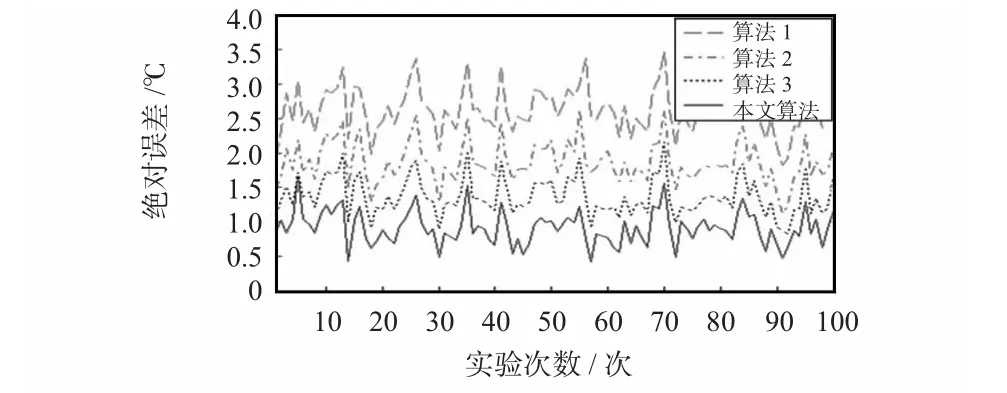
图2 四种方法的绝对误差Fig 2 Absolute error of four methods

4.2 能耗结果分析

本文算法与传感器节点将采集的数据直接发送给汇聚节点的算法相比，节点的平均能耗如图3 所示。经多次实验表明:随着在传感器节点数据预处理阶段设置的阈值δ的增加，节点可节约较多的能量;但为了保证融合的精确度，阈值不能无限增大。在本文实验中，当阈值δ=5 时，可达到最好的节能效率，可节能27.87%，并保证数据融合的精确性。

图3 节点平均能耗Fig 3 Average energy consumption of node

5 结束语

本文提出一种改进支持度的节能型数据融合算法，该算法首先在感知节点对数据进行初次融合处理，然后将初次融合后的数据发送到汇聚节点，采用基于改进支持度函数进行二次融合，以达到降低节点能耗和提高数据融合精度的目的。使用Matlab 7.0 进行仿真的结果表明:运用本文提出的算法，当节点在数据初次融合时选择最适当的阈值δ=5，节点可节能27.87%，最终数据融合的绝对误差均值约为0.98 ℃。

［1］ Bleiholder J，Naumann F.Data fusion［J］.ACM Computing Surveys，2008，41(1):1－41.

［2］ Luo R C.Multi－sensor fusion and integration:Approaches，applications，and future research directions［J］.IEEE Sensors Journal，2002，2(2):107－111.

［3］ Yager R R.The power average operator［J］.IEEE Transactions on Systems，Man，and Cybernetics，2001，31(6):724－731.

［4］ 孙 勇，景 博.基于支持度的多传感器一致可靠性融合［J］.传感技术学报，2005，18(3):537－539.

［5］ 张建业，王占磊，张 鹏，等.基于支持度的限定记忆二次融合算法［J］.计算机应用研究，2012，29(4):1338－1340.

［6］ 王 华，邓 军，王连华，等.改进的一致性数据融合算法及其应用［J］.中国矿业大学学报，2009，38(4):590－594.

［7］ 周 尧，姜礼平，刘 杨.复杂环境下基于支持度的多传感器数据融合算法［J］.火力与指挥控制，2014，39(3):12－15.

［8］ 张 鹏，张建业，王占磊，等.基于邻近量测认知信息的多传感器融合估计［J］.计算机工程，2012，38(8):1－3.

［9］ 张 强，杨 涛.用于环境监测的自供电传感器网络［J］.仪表技术与传感器，2008(2):34－36.

［10］林 薇，祝启龙.无线传感器网络节能型数据融合算法［J］.哈尔滨工程大学学报，2011，32(10):1386－1390.

［11］刘思峰，谢乃明，Jeffery F.基于相似性和接近性视角的新型灰色关联分析模型［J］.系统工程理论与实践，2010，30(5):881－887.