一种基于传感器的测量目标运动参数方法研究

常景娜，高慧斌，乔冠宇

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033;2.中国科学院大学，北京100039)

0 引 言

光电经纬仪对目标进行跟踪测量［1］时，目标的运动参数是确定捕获和瞄准技术要求的主要依据。将目标的运动参数反馈给光电经纬仪的伺服控制系统或武器平台的发射系统，作为目标继续捕获或攻击参数确定的参考。因此，提高目标运动参数的精度，在经纬仪目标跟踪测量中具有非常重要的现实意义。

为了获得目标的速度，首先要根据经纬仪输出的测量数据计算目标的空间坐标;其次，拟合目标的运动轨迹，采用相应的数据处理方式得到目标的运动参数。动态目标的跟踪测量一般选用两台或两台以上的光电经纬仪对目标进行交会跟踪测量。多站交会测量［2，3］时，多台经纬仪要满足多站布站的原则，测量数据较多，需切换交会公式，因此，数据的利用率低，且带来较多的误差项，后续误差计算较麻烦;对于双站交会测量［4］方法，当目标位于两台经纬仪基线上方时，交会精度不高，测量数据不可用;采用一台光电经纬仪匹配激光测距传感器［5］，根据其输出的角度值和距离值就可以确定目标的空间坐标，适用于靶场光电测量试验和外场试验，但易发生单站丢失目标的情况，且测量精度低于双站交会测量方法。目前，应用在经纬仪上拟合目标运动轨迹的方法大多采用最小二乘法［6～9］，最小二乘法是根据均方根误差最小的原理得到目标的运动轨迹。对于做复杂运动，且速度较快的目标来说，要达到较高的拟合精度，拟和函数的阶次较高，计算量大，实时性不好。

本文提出了一种两台经纬仪仅一台匹配激光测距仪，单站、双站综合测量目标空间位置;采用三次样条插值函数拟合目标运动轨迹的测量方法。相比于传统方法，既避免了一台经纬仪测站丢失目标的情况，又具有较高的测量精度;且三次样条插值函数具有二阶光滑度和良好的收敛性，在理论和应用上均有重要意义。

1 激光测距传感器

激光测距传感器是通过测量激光往返目标所需时间来确定目标距离的一种传感器。光电经纬仪上安装的激光测距子系统由激光器、激光发射装置、激光接收装置以及处理电路组成。传感器工作时，由激光二极管向目标发射脉冲极窄的激光脉冲，经目标反射后激光脉冲向各个方向散射，部分散射光返回到传感器的接收装置，记录并处理从激光脉冲发出到返回被接收所经历的时间，即可确定目标的距离，如式(1)所示

其中，R 为目标距光电经纬仪的距离，c 为光速，t 为激光脉冲从发射到返回接收器的时间。本文采用的激光测距传感器测量距离可达6 000 m，当测量距离小于2 000 m 时，测距精度为0.2 m。

2 空间坐标测量原理

将满足交会测量条件的两台光电经纬仪其中一台安装激光测距装置，两台经纬仪的布站方式如图1 所示。OXYZ为发射坐标系，两台经纬仪的光心位置分别为O1，O2，两测站之间的距离为L，基线与X 轴正向的夹角为φ。以O1，O2为坐标原点建立符合右手定则的坐标系O1X1Y1Z1，O2X2Y2Z2。为简便起见，布站时将坐标原点O1，O2和O 设置于同一平面内，且坐标轴的方向一致。在发射坐标系下，两测站原点的坐标分别为(X10，Y10，Z10)，(X20，Y20，Z20)。目标沿M0M1M2…Mn轨迹飞行，在测量水平面的投影为M0'M1'M2'…Mn'。在跟踪测量的ti时刻，目标位于Mi点，两台光电经纬仪测得的方位角和俯仰角分别为A1i，A2i，E1i，E2i，由三角形正弦定理，可得目标在发射坐标系下基于A 站O1X1Y1Z1的空间坐标方程，如式(2)所示

根据函数误差传递原理对式(2)中的各自变量分别求偏微分，易知，当目标位于两台经纬仪基线上方时，(A2i－A1i)约等于π，分母上sin2(A2i－A1i)为极小值，给空间坐标带来较大的测量误差。这时，采用激光测距仪输出的空间距离和经纬仪输出的测角数据，通过式(3)实现单站空间定位，可以有效地避免双站交会带来的测量误差。由此可见，采用单站、双站交会综合测量的方法可以有效地提高目标空间位置的测量精度

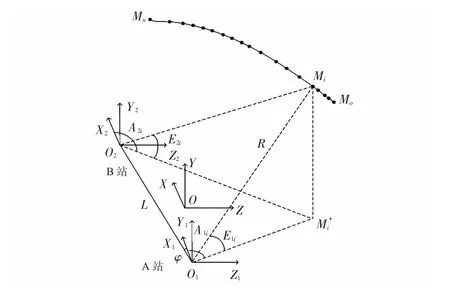
图1 经纬仪布站图Fig 1 Station-distribution of theodolite

3 建立三次样条插值函数

根据光电经纬仪输出的数据可以得到目标各时间节点的空间位置，获得目标的离散空间运动轨迹。为了获取目标的连续运动轨迹往往需要求出不在时间节点上的目标方位坐标，因此，选择插值方法来获得目标运动轨迹的变化规律。

三次样条插值函数由分段三次曲线并接而成，不仅在连接点上二阶导数连续、具有二阶光滑度，还克服了高次插值既不收敛又不稳定的特点，因此，更适合于目标运动参数的求取。将目标的复合运动分解成X，Y，Z 三个方向的分运动，沿X，Y，Z 三个方向随时间变化的分量分别为(ti，Xi)，(ti，Yi)，(ti，Zi)。其中，在ti～ti+1时间段中，X 方向上的三次样条插值函数如式(4)所示

其中，hi为步长。

利用起始点和终止点的导数值已知并连续的条件建立固支样条可得矩阵式(5)，并求得N0N1N2…Nn

得到目标在各时间节点间的三次样条插值函数，对目标各方向分运动函数分别求取一阶导数，就可以得到目标在X，Y，Z 三个方向分运动的速度值。

4 实验结果与分析

为验证本文提出算法的合理性与可靠性，根据现有的实验条件设计以下实验予以验证。在图1 所示的坐标系下，目标沿M0M1M2…Mn轨迹做跃升机动运动。两台经纬仪分别位于目标轨迹的两侧，A，B 两观测站相对于发射坐标系的坐标分别为(－900，0，－200)m 和(1200，0，200)m。为了充分验证本文提出方法的可靠性，实验将分为两部分进行，首先根据两台光电经纬仪和激光测距仪输出的数据计算目标的空间位置、拟合目标的运动轨迹、计算运动参数，然后对比本文提出方法与传统方法的测量精度。

通过A，B 两台光电经纬仪输出的角度信息采用交会测量方法利用式(2)可计算目标的空间位置;当目标位于两台经纬仪基线上方时，采用A 站光电经纬仪输出的方位角、俯仰角和激光测距仪输出的目标距离通过式(3)得到目标的空间位置。两台经纬仪匹配编码器的测角精度均为20″，激光测距仪的测距精度为0.2 m(R ＜2 000 m)，由函数误差传递原理求得目标空间位置的测量精度，目标空间位置坐标及测量误差如图2 所示。由图易知，当目标位于两台经纬仪基线上方时，测量精度出现极大值，给空间位置测量带来极大的误差。因此，采用本文提出的空间坐标计算方法可以有效地减小空间坐标的测量误差。

将目标的空间运动分解到X，Y，Z 三个方向，由上述得到的目标在各时间节点的空间坐标，以及目标在起始点和终止点的速度分量建立固支样条，通过式(4)、式(5)计算目标在各时间段的三次样条插值函数，获得目标的分运动轨迹，如图3 所示。由矢量合成方法得到目标的空间运动轨迹如图4 所示，符合目标的跃升机动运动状态。

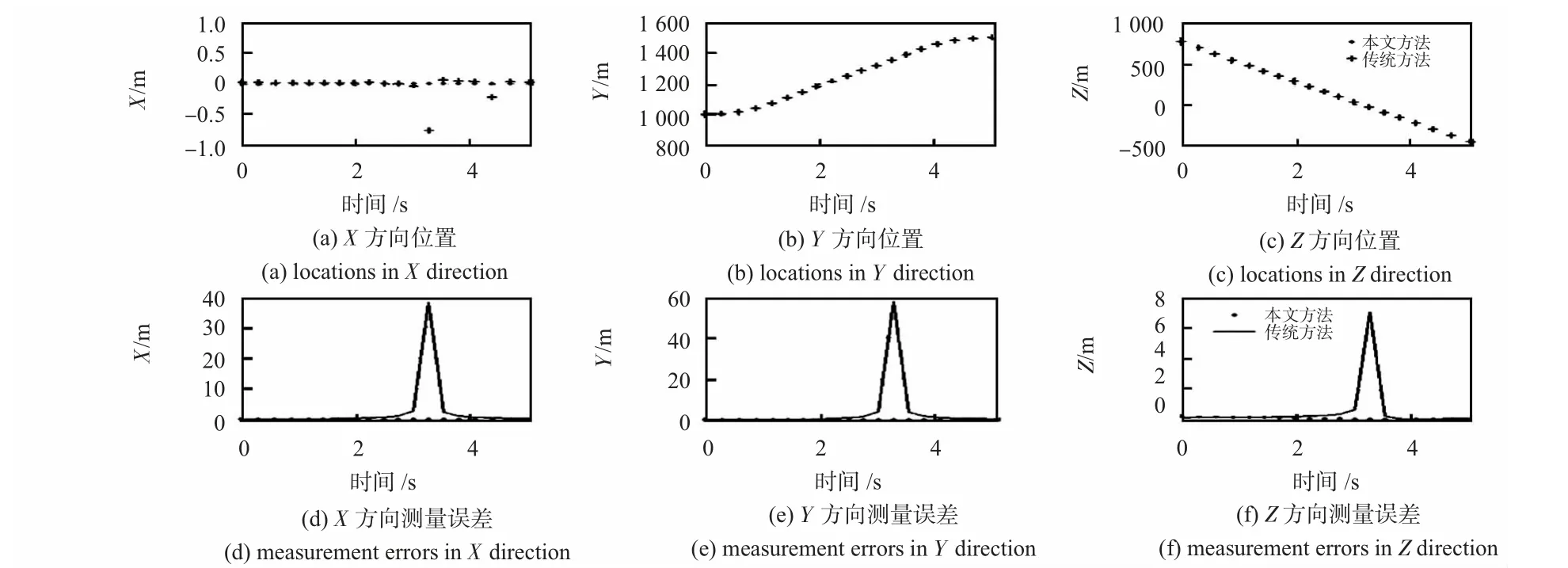
图2 目标的空间位置坐标与测量误差Fig 2 Spacial position coordinates of target and measurement errors

图3 目标分运动轨迹Fig 3 Moving track of target

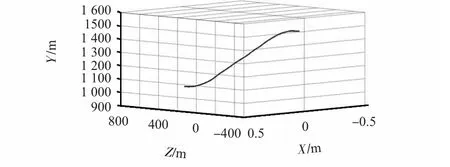
图4 目标的空间运动轨迹Fig 4 Spacial moving track of target

对目标的分运动轨迹进行数据处理得到目标的速度，如图5 所示。由轨迹图和速度图易知，目标在空间内做跃升机动运动。在X 轴方向上基本没有位移，速度趋近于零;在Y 轴方向上，目标从1000 m 跃升到1500 m，随着跃升高度的增加，速度先增加然后保持稳定又逐渐降低;在Z 轴方向上，从Z 轴的正向运动到了Z 轴的负向，速度始终为负值，在跃升运动的初始阶段速度加速降低，随后保持平稳，最后又加速降低，反映了目标先平稳飞行然后机动跃升再平稳飞行的实际情况。

图5 目标分速度曲线图Fig 5 Velocity components curves of target

由误差传递原理易知，利用三次样条插值方法拟合目标的运动轨迹，在X，Y，Z 三个方向的测速精度分别为0.194，0.514，0.347 m/s。由此可见，三次样条插值方法可以很好地拟合目标的运动轨迹，在测量距离不超出2 000 m的空间范围内测速精度可以达到0.649 m/s，测速精度提高了0.351 m/s。同时，三次样条插值方法的数据处理速度优于传统方法，更适合应用于实际目标的实时跟踪。

5 结 论

本文结合光电经纬仪伺服控制系统的需求，提出了一种计算目标运动参数的新方法。本方法主要基于空间坐标理论和曲线拟合的相关算法，首先将光电经纬仪和激光测距仪输出的测量数据转换成目标的空间坐标，其次采用三次样条插值方法拟合目标的运动轨迹，最后通过数据处理得到目标的运动参数及其测量精度。实验证明:该方法提高了目标运动参数的测量精度，在X，Y，Z 各方向上测量误差都在0.6 m/s 以内，验证了该方法的可行性。

［2］ 贾 涛，吴能伟，陈 涛.光电经纬仪组网测量位置估计的Cramer－Rao 限［J］.光电工程，2005，32(7):4－6.

［3］ 顾 青，毛建民.光电经纬仪空中轨迹交会测量方法研究及误差分析［J］.地矿测绘，2009，25(1):12－14.

［4］ 谭振江，郭丽虹，于 涌，等.经纬仪目标交汇测量及航迹曲线拟合［J］.光电工程，2002，29(6):17－20.

［5］ 张黎明，张 毅，赵 欣.基于TDC 的激光测距传感器飞行时间测量研究［J］.传感器与微系统，2011，30(12):71－72.

［6］ 蔡 山，张 浩，陈洪辉，等.基于最小二乘法的分段三次曲线拟合方法研究［J］.科学技术与工程，2007，7(3):352－355.

［7］ 陈岚峰，杨静瑜，崔 崧，等.基于Matlab 的最小二乘曲线拟合仿真研究［J］.沈阳师范大学学报，2014，32(1):75－79.

［8］ Jens Hacker，Bernd－H Kroplin.An experimental study of visual flight trajectory tracking and pose prediction for the automatic computer control of a miniature airship［J］.SPIE Intelligent Computing，2003，5103(3):25－36.

［9］ 李庆扬，王能超，易大义.数值分析［M］.北京:清华大学出版社，2001:90－97.