汇聚太阳能流体流速对吸热器温度场和应力场影响

张 淳，王富强，谭建宇，来庆志

(1．中国机械设备工程股份有限公司，北京 100055;

2．哈尔滨工业大学(威海)汽车工程学院，山东 威海 264209)

0 前言

国际上太阳能热动力发电的聚光系统主要有三种形式:槽式，塔式和碟式［1］。槽式聚光系统太阳能热动力发电技术的优点是:容量可大可小;吸热器和聚光系统都布置于地面上，安装和维护方便;各聚光系统可同步跟踪，控制系统成本低［2］。目前只有槽式聚光系统太阳能热动力发电技术已商业化运行，而含有塔式聚光和碟式聚光太阳能热动力发电技术仍处于实验和示范阶段［3］。

入射太阳光经过槽式聚光系统反射后汇聚在管式吸热器外表面的下半段。管式吸热器外表面的下半段受到高汇聚、非均匀热流密度的照射，而管式吸热器外表面的上半段却受到非汇聚的低太阳热流密度的照射［4］。因此，管式吸热器外表面的热流密度场分布为高度非均匀的，管式吸热器容易承受大温度梯度并引起高热应力而导致吸热器的失效［5］。

为了降低吸热器的热应力，Verlotski 等通过控制流体速率达到降低吸热器热应力的目的［6］;Flore等提出了一种铜－不锈钢双层管式吸热器［7］;Lata等采用高镍合金替代奥氏体不锈钢作为管式吸热器材料来实现热应力降低的目的［8］。采用实验方法研究太阳能吸热器的热应力及热变形是多数学者采用的方法;即便采用数值模拟的方法研究吸热器的温度场和热应力场的过程中，多数学者也是采用了简化的热流密度场或温度场作为热分析的边界条件［9］。为此，本文作者曾采用蒙特卡洛与有限元相耦合法分析了管式吸热器的温度场和热应力场［10］。

本文采用光热力顺序解耦计算法研究流体流速对管式吸热器的温度场、热应变以及热应力场的影响。相关计算结果可以为实际运行过程中防止运行温度过高以及对热应变和热应力的抑制提供参考。

1 光热力顺序解耦计算法

在光热力顺序解耦计算过程中，管式吸热器外表面热流密度场的计算采用本文作者等根据蒙特卡洛法编写的程序代码进行计算［11］。蒙特卡洛法作为一种概率统计的数值计算方法，具有物理概念清晰、对复杂问题适应性强等优点而被计算物理学界广泛应用。采用蒙特卡洛法求解太阳能聚集传输问题的基本思想是:将太阳能看作是大量的、独立的太阳光线组成;为了保证太阳光线分布的均匀性，假设每根光线携带相同的能量;将每根光线的传输过程分解为发射、反射、透射及吸收等一系列相互独立的子过程，每个子过程都遵循特定的分布函数概率模型［12－13］。

在整个热流密度场计算过程中，采用自编网格节点划分程序将管式吸热器的外表面离散成轴向为300 个节点、径向为300 个节点的网格。在光热力顺序解耦计算过程中热流密度场计算的边界条件为:太阳光不平行度为16';太阳辐照度为1 000 W/m2;环日比为0．05;忽略跟踪误差、指向误差及位置误差等对热流密度场分布的影响。在光热力顺序解耦计算过程中采用的槽式聚光系统、管式吸热器及玻璃罩的几何尺寸和物性参数如表1 所示。在实际应用中，多根管式吸热器串联到一起可达上百米。为了计算简化，本文仅取流体入口处2 m 长管式吸热器作为研究对象。

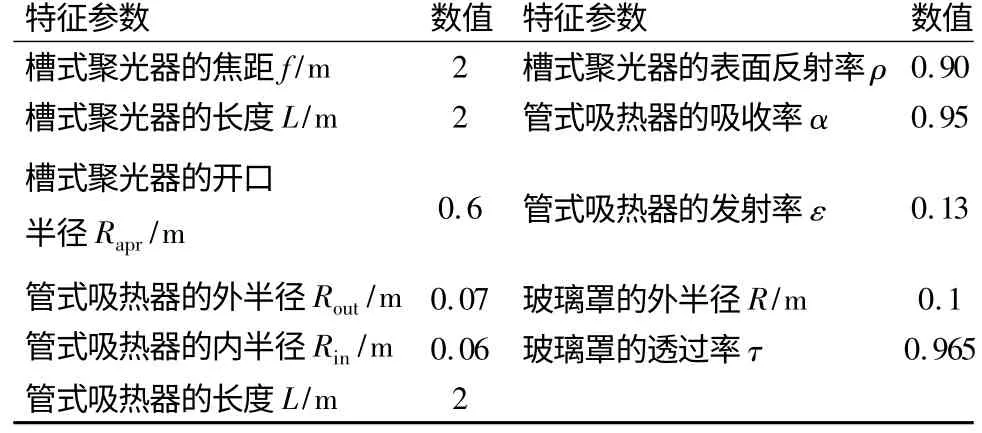
表1 槽式聚光系统和管式吸热器的几何尺寸及物性参数

为了增加管式吸热器的玻璃罩对入射太阳能光线的透射率以及降低吸热器热损失，管式吸热器的玻璃罩会敷有选择性透过涂层。此外，管式吸热器的金属表面还会涂以选择性吸收涂层。管式吸热器金属表面的选择性吸收涂层在太阳光谱下的高吸收率和工作温度下的低发射率不但可以提高吸热器对入射太阳光的吸收，还可以有效的降低吸热器的辐射换热损失。由表1 可知，管式吸热器玻璃罩的透过率高达0．965，非常接近于1．0，而且玻璃罩的厚度非常薄，仅为1．9 ×10－3m［14］，玻璃罩对管式吸热器金属表面的热流密度场的数值大小及分布影响非常小，因此本文在光热力顺序解耦计算过程中将不考虑玻璃罩对管式吸热器表面热流密度分布的影响。

本文采用蒙特卡洛法计算得到的管式吸热器外表面下半段的热流密度分布如图1 所示。为了将计算得到的热流密度导入到温度场计算中，采用拟合函数法将计算得到的管式吸热器外表面下半段的热流密度分布进行多段函数拟合，并作为管式吸热器温度场分析过程中的第二类边界条件。拟合函数得到的热流密度场与计算得到的热流密度场吻合良好，拟合误差小于0．01%［10］。

将温度场分析得到的网格节点温度场通过插值的形式映射到有限元热应力分析网格节点上，并作为体力载荷施加在后序的热应力场分析中，并作为热应力场分析的输入载荷。本文对管式吸热器的热应力场分析过程中无外部边界约束，因此管式吸热器热应力的产生是由于吸热器壁面上不均匀温度分布而引起的。关于光热力顺序解耦计算法的更详细介绍及相关的模型验证，请参见文献［5，10－11，13］。

图1 管式吸热器外表面下半段的热流密度场分布

2 计算网格划分

在采用有限元进行热应力场分析的过程中，模型的网格划分质量对求解结果的精度有着重要的影响;提高网格划分质量，减少离散化随意性带来的误差是有限元分析过程中的重要工作。原则上，Ansys有限元分析只要求网格划分质量在0．2 以上即可计算求解;但是有限元分析过程中的网格质量不高会带来计算时间长、收敛稳定性差、甚至计算结果不准确等缺点［10］。

图2 温度场分析和热应力场分析的网格划分

为了更加精确的捕捉热应力沿吸热器管壁径向和切向方向的分布，在热应力分析过程中的管壁网格划分密度比温度场分析过程中的管壁网格划分密度高。本文采用Ansys Workbench 中提供的ICEM网格划分模块对管式吸热器的流体及管壁几何模型进行网格划分，网格划分过程中采用映射网格技术产生O 型结构化四面体网格。网格划分结果如图2所示，其中用于温度场计算分析的网格划分单元数为95 888，用于热应力场网格划分单元数为175 168。在进行温度场和应力场分析前的网格无关性检查中发现，本文划分的网格单元数足以保证计算精度。网格质量检查结果表明用于温度场分析的网格划分质量均在0．65 以上;用于热应力场分析的网格划分质量更高，均在0． 95 以上，远远高于Ansys 有限元分析的网格划分质量要求。

3 流速对温度场分布的影响

图3 所示为不同流速下管式吸热器出口端面处温度场分布。由图3 可知，随着流体流速的增加，管式吸热器出口端面处的温度迅速的降低;流体未被加热区域也不断的增大。当流体流速为0． 1 m/s时，管式吸热器出口端面处的最高温度为430 K;而当流体流速增加到0．5 m/s 时，管式吸热器出口端面处的最高温度仅为350 K。

图4 所示为不同流速下管式吸热器内壁面温度场沿长度方向分布。由图可知，对于流体流速为0.3 m/s 和0．5 m/s 两种计算工况，入口段的温度分布沿吸热器长度方向迅速地增加(z≤0．1 m)，而后温度沿长度方向的增加速度变缓，温度分布趋于线性增加;对于流体流速为0．1 m/s 的计算工况，在整个管式吸热器长度下温度场沿长度方向都是迅速增加。

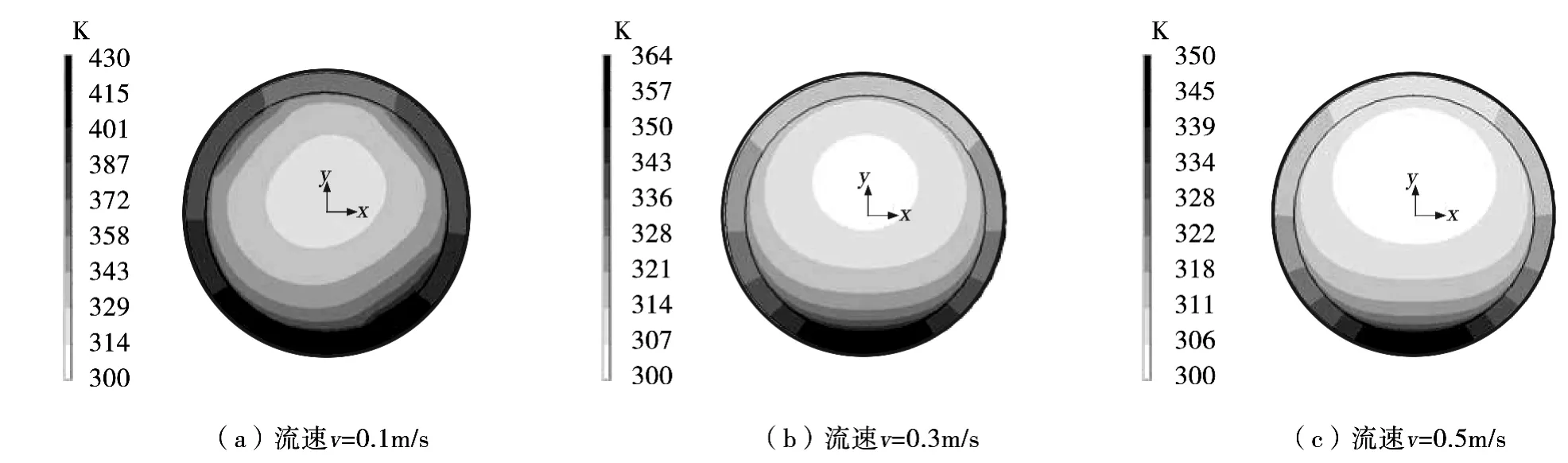
图3 管式吸热器出口端面处温度场分布

4 流速对总应变分布的影响

图5 所示为不同流速下管式吸热器出口端面处的总应变沿圆周角分布。由图可知，管式吸热器的总应变随着流体流速的增加而迅速的降低，当流体流速由0．1 m/s 增加到0．5 m/s 时，总应变由4．14×10－4降低到0．62 ×10－4。在流体流速为0．1 m/s和0．3 m/s 两种计算工况时，总应变沿圆周角分布趋势是一致的:总应变的最大值都出现在圆周角为270°的位置处，两条曲线都在圆周角为38°、140°、234°及305°四个位置处出现了曲线的拐点。流体流速为0．1 m/s 管式吸热器的总应变与流体流速为0．3 m/s 管式吸热器的总应变相差不大，流体流速为0．1 m/s 时的管式吸热器总应变比流体流速为0．3 m/s 的管式吸热器总应变稍高一点，总应变最高差值为22%，出现在圆周角为78°位置处。

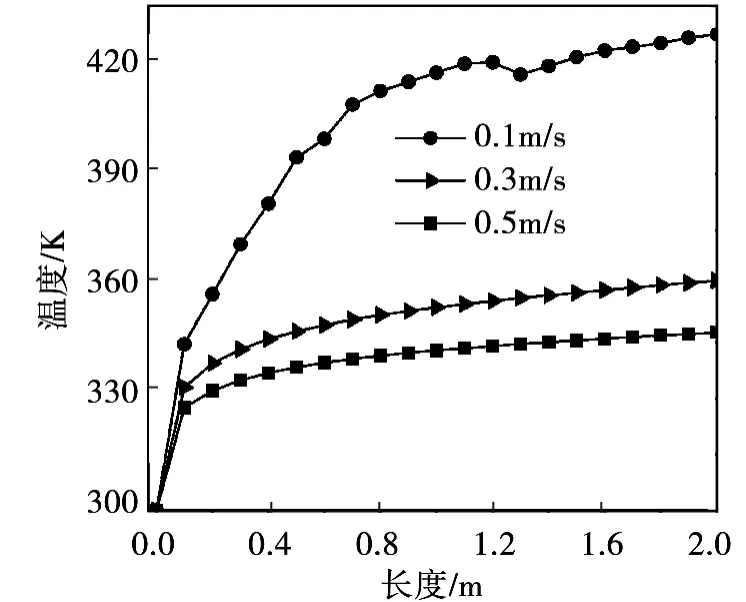
图4 管式吸热器内壁面温度沿长度分布

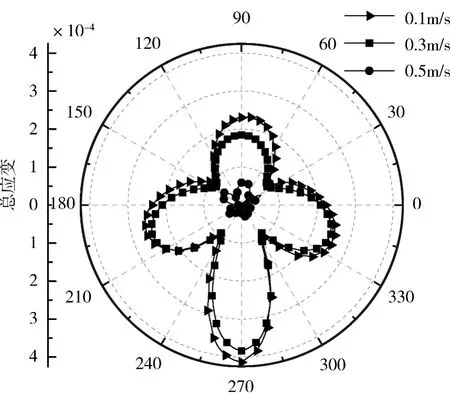
图5 管式吸热器出口端面处总应变沿圆周角分布

5 流速对热应力场的影响

图6 所示为不同流体流速下管式吸热器内壁面轴向热应力沿长度方向分布。由图可知，轴向热应力随着流体流速的增加而降低。在三种不同流体流速计算情况下，管式吸热器入口端面处的轴向热应力均呈现为拉应力且数值非常小，接近于零;随着长度的不断增加，轴向热应力迅速的由拉应力转变为压应力，并且达到一个很高的、接近各自曲线最大值的压应力;在管式吸热器出口端面处，轴向热应力迅速的降低到接近于零。引起这种现象的原因如下:管式吸热器外表面圆周角为270°的位置处受到的热流密度最大，温度也最高;管式吸热器外表面圆周角为270°的位置受到高温后的膨胀速度比周边位置膨胀速度快，因此圆周角为270°的位置会受到来自周边温度相对低、膨胀速度相对慢的位置的约束，造成管式吸热器中间段区间内的轴向热应力为压应力而非拉应力;而在管式吸热器两端面处，两个端面为自由膨胀端，没有外界约束，可以自由的沿轴向方向的两端面处膨胀，因此两端面处轴向热应力比较小，而且接近于零。

图6 管式吸热器内壁面轴向热应力沿长度分布

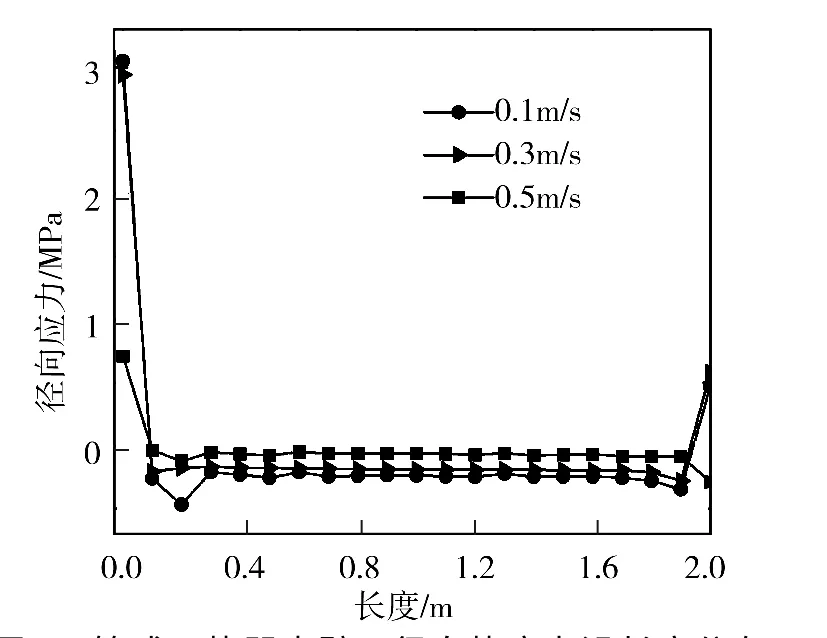
图7 管式吸热器内壁面径向热应力沿长度分布

图7 所示为不同流体流速下管式吸热器径向热应力沿长度分布。由图可知，径向热应力随着流体流速的增加而降低。三种不同流体流速计算情况时，管式吸热器的径向热应力随着长度的增加，迅速的由入口端面处的拉应力变为压应力;在管式吸热器长度为0．1 m 到1．9 m 区间内，三种不同流体流速情况时管式吸热器的径向热应力均变化不大，维持在接近于零的压应力。在管式吸热器出口端面处，三种流体流速情况时管式吸热器的径向热应力又迅速的由压应力变为拉应力。三种不同流体流速情况时的管式吸热器最大径向热应力都出现在吸热器入口处。

图8 所示为不同流体流速下管式吸热器切向热应力沿长度分布。在管式吸热器两端面处的切向热应力的数值远高于沿吸热器长度方向其他位置处的切向热应力的数值。在管式吸热器入口端面处，切向热应力表现为拉应力，沿着吸热器长度的增加，切向热应力迅速的由拉应力转变为压应力。在管式吸热器长度0．1 m 到1．9 m 的范围内，三种不同流体流速情况时管式吸热器的切向热应力均表现为压应力，且三种不同流速情况时管式吸热器的切向热应力都各自维持在一个稳定值附近变化。在相同位置处，切向热应力随着流体流速的增加而降低。与轴向热应力和径向热应力相比，切向热应力的最大值大于轴向热应力和径向热应力。

图8 管式吸热器内壁面切向热应力沿长度分布

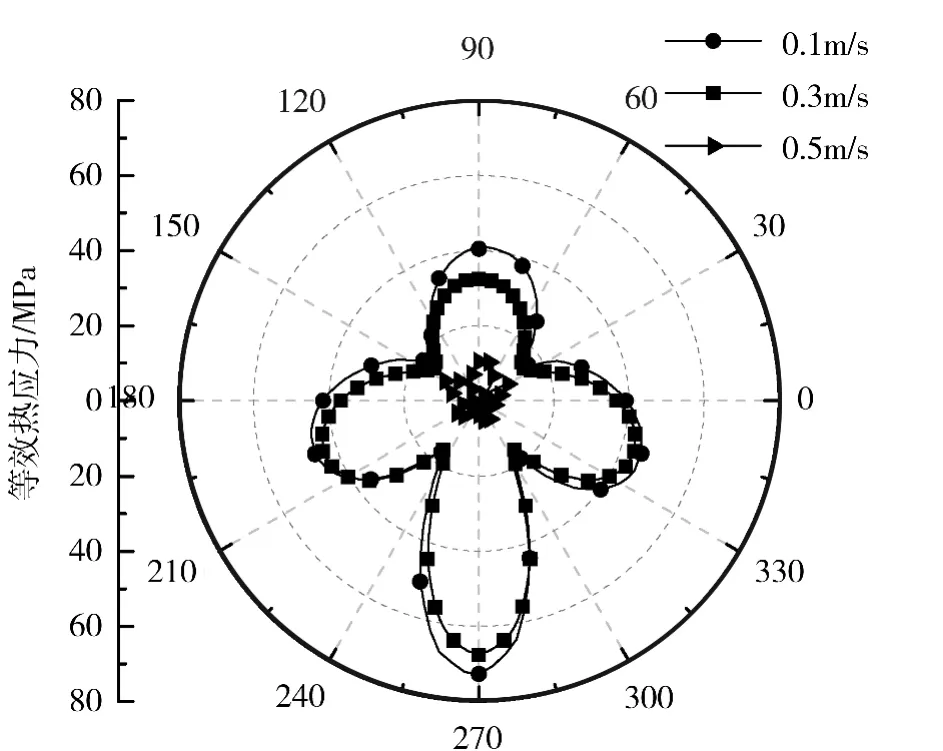
图9 管式吸热器出口端面处等效热应力沿圆周角分布

由形变应变能理论可知，等效热应力与径向热应力、轴向热应力和切向热应力的关系为［15］

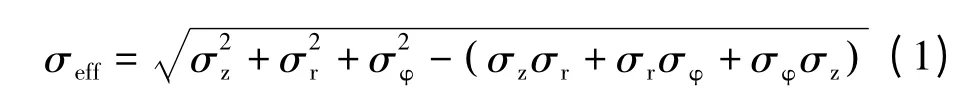
式中 σr、σz、σφ和σeff——径向热应力、轴向热应力、切向热应力和等效热应力。

图9 所示为不同流体流速下管式吸热器的出口端面处等效热应力沿圆周角分布。由图可知，管式吸热器的等效热应力随流体流速的增加而迅速降低。当流体流速由0．1 m/s 增加到0．5 m/s 时，管式吸热器的等效热应力由72． 7 MPa 降低到10．9 MPa。与总应变沿圆周角分布规律一样，在流体流速为0．1 m/s 和0．3 m/s 两种计算工况下，等效热应力沿圆周角分布趋势是一致的，等效热应力的最大值都出现在圆周角为270°的位置处，两条曲线都在圆周角为38°、140°、234°及305°四个位置处出现了曲线的拐点。根据公式(1)可知，与轴向热应力和径向热应力相比，切向热应力对管式吸热器的等效热应力贡献比例更大。因此，均匀化温度沿管式吸热器圆周方向的分布是热应力抑制的有效手段之一。

综合以上分析，本文数值计算结果与Verlotski［6］的实验结论相类似，通过控制流体的流速可以有效的降低管式吸热器的总应变及等效热应力。

6 结论

本文采用光热力顺序解耦计算法分析了流体流速对管式吸热器温度场、总应变及热应力场的影响。计算结果表明管式吸热器的温度场、总应变及等效热应力均随着流体流速的增加而降低，控制流体速率可以有效的降低管式吸热器的总应变和热应力。与轴向热应力和径向热应力相比，切向热应力对管式吸热器的等效热应力的贡献比例更大。因此，均匀化温度沿管式吸热器的圆周方向分布是热应力抑制的有效手段之一。

［1］屠楠，魏进家，方嘉宾．太阳能腔式吸热器表面反射率的选择［J］．工程热物理学报，2014，35(4):700 －704．

［2］何梓年．太阳能热利用［M］．合肥:中国科学技术大学出版社，2009．

［3］Mao Q J，Xie M，Tan H P． Effects of material selection on the radiation flux of tube receiver in a dish solar system［J］．Heat Transfer Research，2014，45(4):339 －347．

［4］Cheng Z D，He Y L，Xiao J，Cui F Q，Du B C，Zheng Z J，Xu Y． Comparative and sensitive analysis for parabolic trough solar collectors with a detailed Monte Carlo ray － tracing optical model［J］．Appl． Energy，2014(115):559－572．

［5］Wang F Q，Shuai Y，Yuan Y，Yang G，Tan H P．Thermal stress analysis of eccentric tube receiver using concentrated solar radiation［J］．Solar Energy，2010，85(10):1809－1815．

［6］Verlotski V，Schaus M，Pohl M． A solar thermal mgopowder receiver with working temperatures of more than 1600℃:model investigation by using laser as an irradiation source［J］．Solar Energy Materials and Solar Cells，1997，45(3):227－239．

［7］Flores V C，Almanza R F． Behavior of compound wall copper－steel receiver with stratified two－phase flow regimen in transient states when solar irradiance is arriving on one side of receiver［J］．Solar Energy，2004(76):195 －198．

［8］Lata J M，Rodriguez M A，Lara M A． High flux central receivers of molten salts for the new generation of commercial stand－alone solar power plants［J］． Journal of Solar Energy Engineering，2008(130):0211002．

［9］Kumar N S，Reddy K S． Thermal analysis of solar parabolic collector with porous disc receiver［J］． Applied Energy，2009(86):1804 －1812．

［10］Wang F Q，Shuai Y，Yuan Y，Liu B． Effects of material selection on the thermal stresses of tube receiver under concentrated solar irradiation［J］．Materials and Design，2012(33):284 －291．

［11］Wang F Q，Shuai Y，Tan H P，Lin R Y，Cheng P． Researches on a new type of solar surface cladding reactor with concentration quartz window［J］．Solar Energy，2013(94):177－181．

［12］Dai G L，Xia X L，Hou G F． Transmission performances of solar windows exposed to concentrated sunlight［J］．Solar Energy，2014(103):125 －133．

［13］Wang F Q，Tan J Y，Ma L X，Wang C C． Effects of glass cover on heat flux distribution for tube receiver with parabolic trough collector system［J］． Energy Conversion and Management，2015(90):47 －52．

［14］Almanza R F，Lentz A，Jimenez G． Receiver behavior in direct steam generation with parabolic toughs［J］． Solar Energy，1997(61):275 －278．