常用太阳跟踪系统接收辐射量的计算

彭 军，杨智奇，董菁雯，虞正发

(1．中国人民大学 农业与农村发展学院，北京 100872;

2．陕西首创天成工程技术有限公司，陕西 宝鸡 721016;3．上海电力设计院，上海 200025)

随着光伏发电规模持续地扩大，太阳跟踪发电系统的可靠性不断提高，建设成本显著下降［1］，该技术逐渐得到社会认可［2］。根据跟踪原理的不同现有太阳能跟踪系统主要可以分为垂直轴跟踪系统、双轴跟踪系统和斜单轴跟踪系统(图1)。因图1(a)和图1(c)在国内光伏电站中较为常见，本文着重分析该种跟踪系统的太阳能辐射量的接收特点。

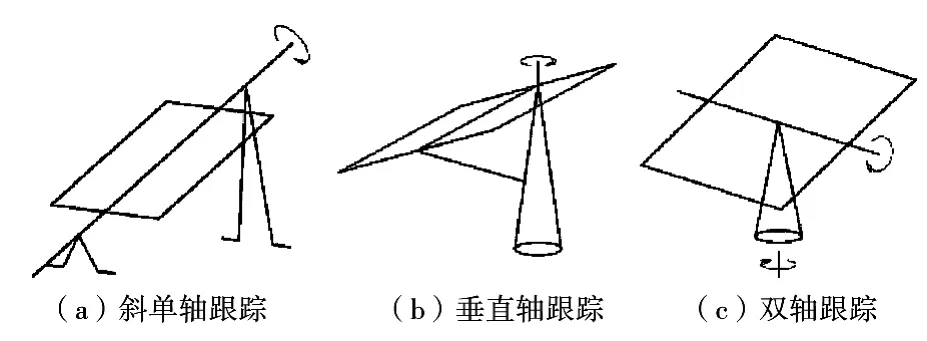
图1 太阳跟踪系统的典型类型

光伏发电的储能和上网均要求进行发电出力的短期预测，而气象观测站只提供水平面上的观测值，这就要求能够使用有效计算方法将水平面实测数据推算为跟踪系统的有效接收量。针对这一问题有很多学者从理论和实验两个方面进行了卓有成效的研究。Chang 对斜单轴跟踪系统所接收的地外理论辐射、经验模型的总辐射和实际观测值进行了对比分析［3］。Koussa 通过研究肯定了太阳跟踪系统可以有效增大平板光伏电池的出力［4］。Maatallah 对位于突尼斯蒙耐斯帝尔市的不同太阳跟踪系统的出力进行了分析［5］。Cruz－Peragón 对西班牙25 个城市使用双轴跟踪系统的优越性进行了分析［6］。Koussa重点研究了北非和地中海地区不同太阳跟踪方式对平板光伏发电装置出力的影响［7］。以上文献主要从理论公式或者半经验公式来研究跟踪系统所接收辐射量的变化。本文梳理和总结了现有研究成果，并从理论推导着手，对常用太阳跟踪系统接收辐射量的计算进行了系统阐述，推荐了以实测水平数据作为设计输入的计算方法。

1 太阳光的几何分析

从任意位置太阳辐射接收面的入射角推导过程开始(见图2)。

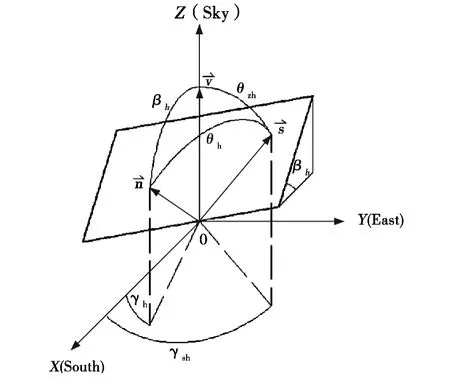
图2 太阳光几何图

以斜面上的任意一点为原点0，做起始于原点的铅垂向量v⇀，斜面法线向量n⇀和入射光向量s⇀。在单位球面上连接三个向量的端点，形成球面nvs。)nv的弧长等于倾角βh，)sn的弧长等于入射角θh，以及)sv的弧长等于天顶角θzh。太阳方位角γsh为太阳入射光在水平面上投影和当地经度线所成夹角。斜面方位角γh为斜面法线在水平面上投影和当地经度线所成夹角。通常定义方位角的边线正向指向赤道为0，偏西为负，偏东为正。对球面nvs 应用余弦定理，得入射角θh的方程［8］

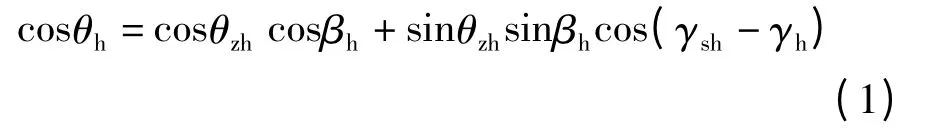
利用地心天球图可直观推导出入射光天顶角和方位角的表达式(见图3)。地球中心位于点0，N 为北极，P 为观测点，Q 为太阳在时角ω 时的位置。

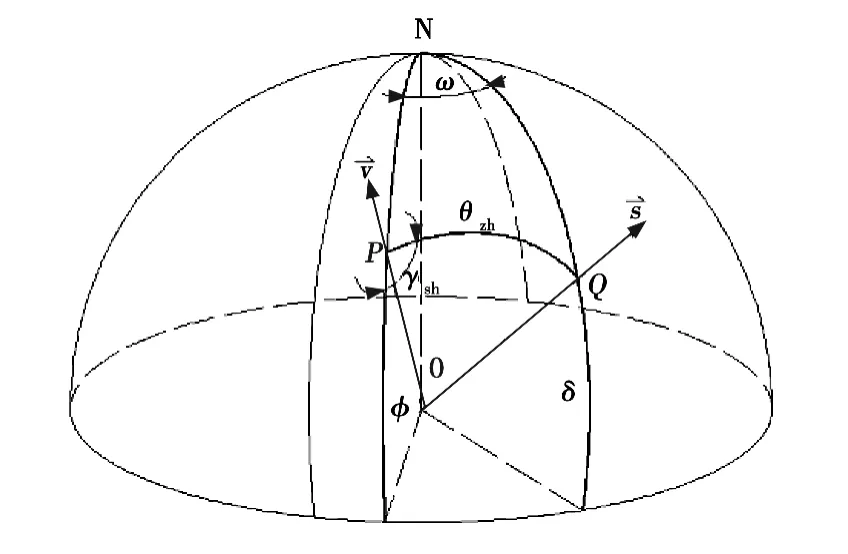
图3 太阳光的地心天球图

以中午12 点为基准0，每偏离1 h 增减15°，上午为负下午为正。同样v⇀为铅垂向量、s⇀为入射光向量，故∠POQ 和)PQ均等于天顶角θzh。利用全年序数日n 可以得到赤纬角δ 的近似表达式［9］

对球面NPQ 运用余弦定理，加之纬度φ 可以得到天顶角θzh的方程

cosθzh=cosφcosδcosω+sinφsinδ (3)

再对球面NPQ 运用正弦定理，可得入射光方位角γsh的表达式

其中

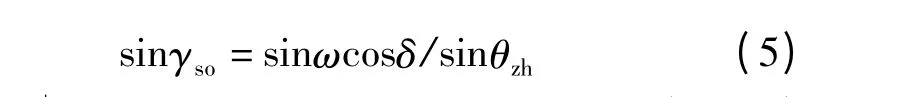
2 计算方法

本文认为完全的理论公式或者半经验公式均难准确地模拟小气候环境下特有的太阳辐射特性。而实测水平面数据是当地有关太阳辐射的综合反映，以此为设计输入的计算结果相较其它方法将更加接近实测结果。因而，该节从任意斜面逐时辐射量的计算出发，结合跟踪系统的运行特点给出了相应倾角和方位角的计算方法。

2．1 斜面逐时总辐射

假设散射光和反射光均为各向同性，根据已有文献斜面逐时总辐射量的计算方法为［10］

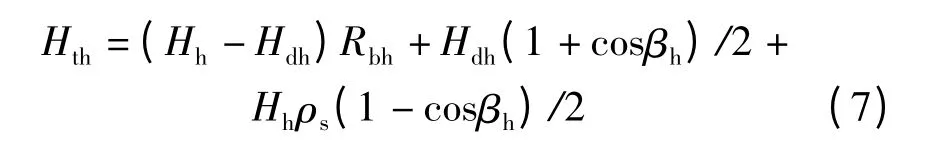
式中的总辐射量Hh和散射辐射量Hdh采用水平面实测数据。βh为斜面相对于水平面的逐时倾角，因跟踪系统的工作原理而异;ρs为地表反射率，温度大于0℃时取0．2，小于－5℃时取0．7，介于两者之间时采用线性插值［11］。

其中直射光增强系数Rbh的计算方法为

当斜面倾角βh和斜面方位角γh为定值时，式(7)和式(8)可用于计算固定倾角系统所接受的辐射量。

2．2 双轴跟踪系统

太阳跟踪系统通过调节方位角或者倾角从而使所接收的直射辐射量实现最大化，对于入射角方程(1)来说就是求cosθh的极大值。双轴跟踪系统通过两个维度的调节总可以令斜面垂直于入射直射光，进而使接收到的直射辐射量最大

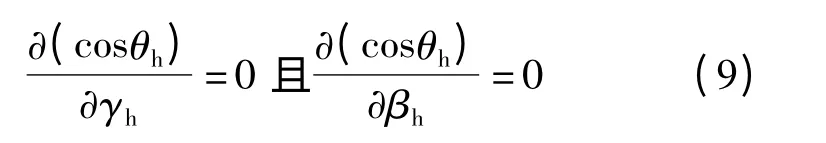
2．3 斜单轴跟踪系统

斜单轴跟踪系统的运动特征是旋转轴的安装倾角β'和方位角γ'固定，并且斜面围绕倾斜轴旋转，进而使所接受到的辐射量尽可能的大。由入射角方程(1)的极值条件和球面三角形的余弦定理可得斜面方位角的表达式

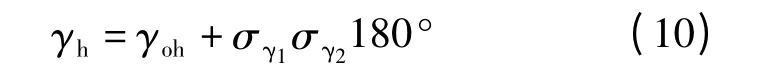
其中

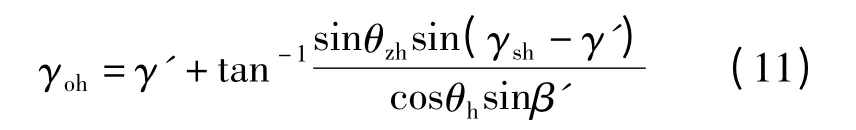
当(γoh－γ')(γsh－γ')≥0 时，σγ1取0 否则为1;当(γsh－γ')≥0 时，取1 否则为－1。

斜面倾角的表达式

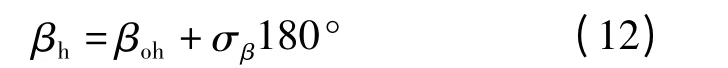
其中

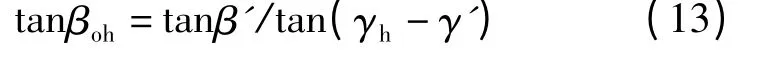
且当βoh≥0 时，σβ取0 否则为1。

3 实验验证

在广东省珠海地区，利用太阳辐射测量仪对水平面、斜单轴跟踪系统和双轴跟踪系统的太阳辐射量的接收状况进行了同步对比观测。实验场所位于N 22°15'、E 113°34'，海拔8 m。斜单轴跟踪的安装倾角为22°，安装方位角为0。选取1 月份的某日实测数据，对本文所述计算方法进行验证(见图4)。

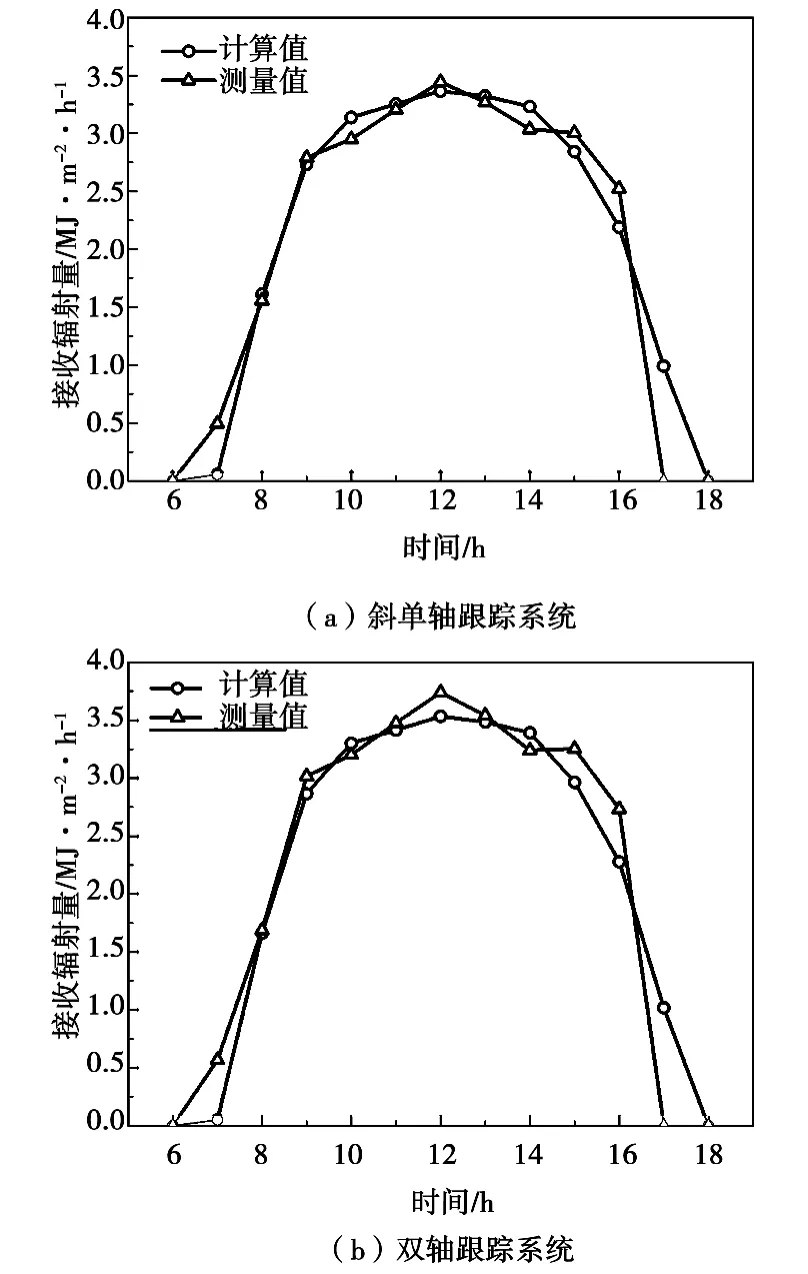
图4 全天逐时辐射量变化对比图

斜单轴跟踪系统的计算值和实测值之间的日接收辐照量的相对误差为1．73%，双轴跟踪系统的同为1．73%。该计算方法总体上可以较好地模拟跟踪系统所接收的辐射量。但是早晨和傍晚的误差较大，这可能与跟踪系统弱光下的灵敏性欠佳有关。

对比分析发现，两种太阳跟踪方式均有助于提高斜面所接收的辐射量。相对于固定安装方式而言跟踪方式在早晨和傍晚的效果尤为显著。但是双轴跟踪方式相对于斜单轴跟踪的优势并不明显。

4 结语

综上研究可知:

(1)本文阐述了常用太阳跟踪系统所接收到的逐时辐射量的计算方法;

(2)以广东省珠海地区某日的观测实验为例，将本文所述方法的计算值与实测值进行了对比分析。结果表明，该方法可以较好地模拟常用太阳能跟踪系统所接收的辐射量。

符号表

Hh——水平面逐时总辐射量;

Hdh——水平面逐时散射辐射量;

Hth——斜面逐时总辐射量;

φ——纬度;

γ'——斜面安装方位角;

β'——斜面安装倾角;

ρs——地表反射率;

Rbh——直射光逐时增强系数;

θzh——入射光逐时天顶角;

n——全年序数日;

δ——赤纬角;

ω——时角;

θh——斜面逐时入射角;

γsh——入射光逐时方位角;γso、ωew、σew、σns、σw——计算入射光方位角过程中的参数;

γh——斜面逐时方位角;

γoh、σγ1、σγ2——计算斜面方位角过程中的参数;βh——斜面逐时倾角;

βoh、σβ——计算斜面逐时倾角过程中的参数。

［1］刘庆才，沈辉． 太阳跟踪装置应用的经济性分析［J］．电源技术，2012，36(10):1489 -1492．

［2］曹石亚，李琼慧，黄碧斌，等． 光伏发电技术经济分析及发展预测［J］．中国电力，2012，45(8):64 -68．

［3］Chang T P． Comparative study on the gain of a tracking panel according to different radiation sources［J］．Journal of the Chinese Institute of Engineers，2010，33(1):131 -139．

［4］Koussa M，Cheknane A，Hadji S，et al． Measured and modelled improvement in solar energy yield from flat plate photovoltaic systems utilizing different tracking systems and under a range of environmental conditions［J］．Applied Energy，2011，88(5):1756 -1771．

［5］Maatallah T，El Alimi S，Nassrallah S B． Performance modeling and investigation of fixed，single and dual-axis tracking photovoltaic panel in Monastir city，Tunisia［J］． Renewable and Sustainable Energy Reviews，2011，15(8):4053 -4066．

［6］Cruz-Peragón F，Casanova -Peláez P J，Díaz F A，et al． An approach to evaluate the energy advantage of two axes solar tracking systems in Spain［J］． Applied Energy，2011，88(12):5131 -5142．

［7］Koussa M，Haddadi M，Saheb D，et al． Sun Tracking Mechanism Effects on Flat Plate Photovoltaic System Performances for Different Step Time and Main Parameters Affecting the Obtained Gains:Case of North Africa and Mediterranean Site［J］．Energy Procedia，2012，18(5):817 -838．

［8］Paulescu M，Paulescu E，Gravila P，et al． Modeling Solar Radiation at the Earth Surface［M］//Weather Modeling and Forecasting of PV Systems Operation． Springer London，2013:127 -179．

［9］Lukaĉ N，Žlaus D，Seme S，et al． Rating of roofs’surfaces regarding their solar potential and suitability for PV systems，based on LiDAR data［J］． Applied Energy，2013，102(2):803 -812．

［10］NASA Surface meteorology and Solar Energy:Methodology［EB/OL］．(2004 -12 -16)［2014 -01 -12］．http://eosweb．larc．nasa．gov/sse

［11］Zhang H L，Baeyens J，Degrève J，et al． Concentrated solar power plants:Review and design methodology［J］．Renewable and Sustainable Energy Reviews，2013，22(6):466-481．