某型AUV对转电机子群协同多目标粒子群优化
王司令 宋保维 段桂林
(1.西北工业大学航海学院 西安 710072 2.中船重工第710所 宜昌 443003)
某型AUV对转电机子群协同多目标粒子群优化
王司令1宋保维1段桂林2
(1.西北工业大学航海学院 西安 710072 2.中船重工第710所 宜昌 443003)
某型自主水下航行器(AUV)需要一种高效、小质量的对转电机,同时要求电机在尾段密闭条件下可长时间航行。针对这一问题,从电机计算模型和多目标优化算法两方面,提出基于电磁-热耦合模型和子群协同的多目标粒子群帕累托最优(MOPSO)设计方法。该模型使用气隙磁场解析法进行电磁计算,使用等效热网络法计算电磁-热耦合情况下的电机温升。利用计算流体力学(CFD)方法计算旋转部件及航行器壳体的对流换热系数,以解决对流等效热阻计算不准确的问题。最后以效率和质量为优化目标,电机温升和几何条件及磁路磁密为约束条件,使用改进的MOPSO方法进行优化,并将优化结果与NSGA-Ⅱ算法优化结果进行比较,结果表明该方法能够获得更接近于真实帕累托前沿的解集,且解集分布性良好。制作样机后进行试验,功率、转速、效率、质量等指标均满足要求,且尾段密闭条件下5 h负载温升符合要求。
自主水下航行器 对转电机 多目标优化 粒子群 电磁-热耦合 计算流体力学
0 引言
自主水下航行器(AUV)具有活动范围大、机动性好、安全、智能化等优点,成为海底考察、数据收集、侦察、布雷、扫雷、援潜和救生等水下任务的重要工具。AUV广泛使用对转电机驱动对转螺旋桨以提高推进效率和平衡AUV的横滚力矩。对转电机一般有两种形式:一种是内外转子共用一套定子;另一种是利用定转子的作用力与反作用力驱使两个转子朝相反方向转动。不同的AUV对于推进电机有不同要求。对于长航时AUV,由于电池电量有限,推进电机必须有足够高的效率;同时应减小质量,避免AUV重心失衡导致运动姿态难于控制的问题。由于推进电机所处的AUV尾段完全密封,使得散热效率降低,还需考虑电机在密闭条件下的温升。
电机的设计是一个包含多变量和多约束的非线性多目标优化问题。国内外一些学者对此进行了相关研究[1-6]。电机的优化模型一般选取集总参数模型或有限元模型;优化算法可使用梯度优化算法、直接搜索算法和遗传算法。文献[1,2]使用改进的遗传算法和集总参数模型对开关磁阻电机进行了优化;文献[3]推导出双转子风力发电机的计算公式,并对齿槽转矩进行了优化;文献[4]利用场路耦合方法计算机桨一体化电机性能,并进行了优化;文献[5]使用有限元模型对汽车用高功率密度电机进行了优化设计;文献[6]使用磁路模型进行了初始优化设计[6]。而AUV用对转电机,目前还无相关优化设计文献。
本文综合考虑计算效率和准确度,提出一种基于气隙磁场解析模型和等效热网络法的AUV对转电机电磁-热场耦合模型,并进行了电机的电磁设计和温度分析。该模型避免了使用集总参数法过于依赖经验参数(如漏磁系数等)的问题,同时相比有限元法计算效率大大增加。使用热网络法计算电磁-热耦合状态下的电机温升。为解决热网络法中对流热阻计算不准确的问题,使用CFD预先计算各旋转部件和壳体的对流散热系数。与有限元计算结果对比表明该模型电磁计算和温度计算均较为准确。最后使用了一种改进的基于子群协同优化的多目标粒子群算法(MOPSO),并将优化结果与NSGA-Ⅱ算法进行了比较。最后选取其中一个方案试制后进行试验,各指标均满足要求。
1 对转电机计算模型
本文中AUV所使用的对转电机结构如图1所示。电机的外转子与内转子通过作用力与反作用力驱动朝相反的两个方向转动。通过法兰盘安装在AUV舱体内侧。考虑到两个转子转动惯量的平衡,将电枢放置在内转子。通过安装在内轴后端的滑环和刷架实现对电枢供电。永磁体以表贴的方式安装在外转子内侧。

①内轴 ②工字钢 ③内转子铁心(轭部) ④电枢端部(前)⑤槽内电枢 ⑥内转子齿部 ⑦电枢端部(后)⑧绕组端部空气(前) ⑨绕组端部空气(后) ⑩气隙 永磁体外转子外壳外转子气隙电机罩壳体外轴AUV后端空气壳体图1 AUV永磁对转电机结构示意图Fig.1 Schematic diagram of permanent magnet counter-rotating rotors motor for AUV
优化参数选取:外转子轭内半径Ro,永磁体厚度hm,气隙长度g,铁心长度Lst,外转子轭部磁密Boc,内转子轭部磁密Bic,齿部磁密Bt。优化选取参数示意图如图2所示。

图2 对转电机设计参数示意图Fig.2 Design parameter schematic of counter-rotating rotors motor
1.1 解析法计算气隙磁密
磁场计算需要在随机或优化过程中给定的优化参数和常数情况下,计算电机的气隙磁场。解析法要求磁路磁导率无限大。因此本文将冲片和外转子轭部磁密限定在膝点附近,先假设磁导率无穷大,通过对外转子轭厚、内转子齿宽、内转子轭厚进行设计,确保永磁体的磁路不出现饱和。对转电机空载气隙磁密为[7]
(1)

(2)
将考虑内转子开槽影响的每极下的气隙磁密积分,即可得到每极磁通量
(3)
假定每极磁通量的一半通过外转子轭,则外转子轭厚为
(4)
同理齿宽和冲片轭厚分别为
(5)
(6)
式中,BIyoke为外转子轭部设计磁密,T。在求得每极磁通量后,可根据空载转速得到每相串联匝数。由电机的功率要求可得到电流值,结合每相匝数即可得到每槽最小截面积。由于生产工艺的不同,可设置不同的槽满率,进而逆向求解得到实际槽面积。以圆底槽为例,再根据平行齿的要求求得槽底圆半径、槽深和槽宽。槽开口宽和齿肩角等由生产工艺和下线的宽度决定。
1.2 对转电机损耗
电机的损耗可分为铜损耗、铁心损耗和机械损耗3部分。铜损耗在内转子中产生,可由绕组电阻和电流得到,并且随温度的升高而增加。由于永磁体与外转子轭相对静止,所以相对频率为零,且由内转子绕组产生的电枢反应磁场相对较小,因此外转子轭磁损耗基本为零,只考虑内转子磁损耗。在本文电机中,永磁体时刻暴露在由内转子绕组产生的高频磁场中,永磁体中会产生涡流损耗。但永磁体的涡流损耗相对较小,因此可忽略。
内转子铁心损耗主要包括磁滞损耗、涡流损耗和附加涡流损耗。磁滞损耗与磁密波形无关,表示为[8]
(7)
式中,f为频率,Hz;Bmax为铁心最大磁密,T;n为Steinmetz常数,由磁密决定,通常在1.5~2.5之间。对于非正弦磁密,涡流损耗和附加涡流损耗为
(8)
(9)
式中,k″e和k″x为修正系数。由于包含两个转动轴,所以对转电机机械损耗包括两个轴承摩擦的损耗及风阻。在密闭情况下圆柱电机的风阻相比损耗,可忽略不计。轴承摩擦损耗为
(10)
式中,Fb为径向负载,N;di为轴承内径,m;fr为轴承摩擦系数;Nb为轴承数。
至此可得到电机的损耗
P=Pcu+Ph+Pe+Px+Pb
(11)
1.3 等效热网络法计算温升
对转电机内外转子均在转动,所以无法通过注入液体的办法进行冷却。为节省电池能量,降低航行噪声,也无法通过加装风扇强制对流进行散热。所以AUV对转电机一般通过自然对流将热量传递至AUV壳体,通过海水散热。本文采用等效热网络法计算电机温升,等效热网络图如图3所示。
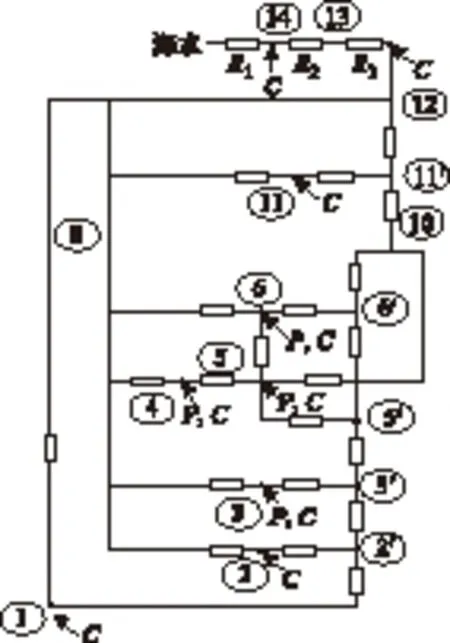
图3 永磁对转电机等效热路图Fig.3 Thermal network of permanent magnet counter-rotating rotors motor
电机的旋转部件均可简化为圆柱体,传导热阻可通过空心圆柱体等效热阻计算公式获得[9]。对流热阻与几何形状和电机转速有关。为准确得到AUV壳体及电机各旋转部件(如外转子端盖,内转子工字钢等)的对流热阻,使用CFD方法计算得到对流换热系数,再根据公式R=1/αA计算等效热阻,其中A为部件面积,α为对流散热系数。当AUV速度为12节,对转转速为1 200r/min时,以AUV壳体为例,对流换热系数计算结果如图4所示。各部分平均对流换热系数计算结果如表1所示。

图4 AUV 壳体散热系数(W/(m2·K))Fig.4 Heat transfer coefficient of AUV shell(W/(m2·K))

壳体后段转子端盖工字钢铁心绕组端部自然对流轴48852522131856
由于转子间的相对运动,电机气隙中的空气受到切向运动的影响,因此,气隙中的气流切向速度呈双曲线型分布[10]。其表面传热系数可表示为
(12)
求解方程(13)可得到电机稳态温升为
(13)式中,C为热容,J/(kg·℃);θ为节点温度,℃;P为每个节点的损耗,W;Yr为热导,W/K;α为温度系数。
1.4 电磁-热耦合计算模型
设计开始阶段设定初始温度。在进行磁场分析和绕组设计后,计算电机损耗,作为热网络的热源。求解热网络中每个节点的温升,进而更新永磁体剩余磁密和电阻率等参数,再次进行求解,直到收敛为止。

图5 电磁-热耦合计算流程Fig.5 Flowchart of the combined electromagnetic-thermal analysis
2 优化过程
2.1 目标函数和约束条件
将优化变量表示为矢量Χ
X=[RohmgLstBocBicBt]T
(14)
根据AUV的总体控制要求和航程需要,确定以质量f1、效率f2为优化目标。
约束条件主要包括AUV尾段密闭情况下的电机温升以及由AUV直径限制的最大电机外径、最长电机轴向长度等。同时,为了使电机的磁路分布更为合理,本文对于槽型也进行了约束,在搜索空间内限制了槽型的深宽比。考虑到制造条件的限制,还设置了最小气隙长度。为了计算获得更精确的磁通量,约束条件还包括冲片各部分及轭部的饱和磁密。因此,对转电机多目标优化问题可表示为
(15)
其中约束条件为
(16)
式中,mc为绕组质量;ms为内转子铁心质量;mp为永磁体质量;mi为外转子轭部质量;Pe为额定功率;SHB为槽深宽比;Tmax为最高温度。
2.2 子群协同多目标粒子群优化方法
传统的电机设计在面对多目标问题时,均是将多目标折合成不同的权重,转换为单目标进行处理,称之为“准”多目标优化。而不同目标的权重基于经验给出,遇到新型电机各权重往往难以确定。本文给出了一种改进的多目标粒子群方法,用以处理AUV对转电机的多目标优化问题。
标准PSO算法的运动方程为[11]
Vi(t+1)=wVi(t)+c1r1(Pi-Xi(t))+c2r2(Pg-Xi(t))
(17)
Xi(t+1)=Xi(t)+Vi(t+1)
(18)
式中,w为惯性权重;c1、c2为加速常数;r1、r2为区间[0,1]内均匀分布的随机数;Pi为粒子自身经历的最好历史位置;Pg为整个群体所经历的最好位置;Xi(t)、Vi(t)分别为微粒在t时刻的位置与速度。本文使用一种改进的基于两个子群体的多目标PSO方法。两个子群体分别进行优化,然后交换两个子群的最优解,作为子群更新速度的全局最优解。为解决解集分布不均和早熟收敛的问题进行部分改进:①通过Pareto前沿集中个体的拥挤距离来判断解之间的疏密程度,拥挤距离大的微粒被保留下来,拥挤距离小的微粒被删除。②在基本种群每次迭代过程中随机选择5%的支配解进行变异操作,以增强算法的全局搜索能力。另外在使用罚函数时,并未直接将违反约束的解剔除掉,而是在进化过程中禁止将粒子引导至不可行解,当不可行解出现在Pareto前沿集中时,才直接剔除。
3 优化结果及试验测试
3.1 优化结果对比
本文针对某型AUV设计一台功率5 kW,对转转速为1 200 r/min的推进电机。常数初始化表格见表2。MOPSO两个子群粒子数均为50个,进化代数100代,惯性权重0.7,c1=0.4,c2=0.5。

表2 常数参数值Tab.2 Constant parameters and their values
基于经验权重系数进行准多目标优化的结果及基于Pareto最优的MOPSO优化结果如图6所示。图6清晰地反映了粒子群的飞行方向不断靠近Pareto前沿。基于权重的准多目标PSO优化结果为Pareto最优结果上的一个点。可以看出,增加电机重量,可提高电机的效率,这是因为增加重量可减小电磁负荷,从而减小损耗。因此,需要在前沿集中根据需要选取一个最佳设计方案,使效率和重量均达到要求。
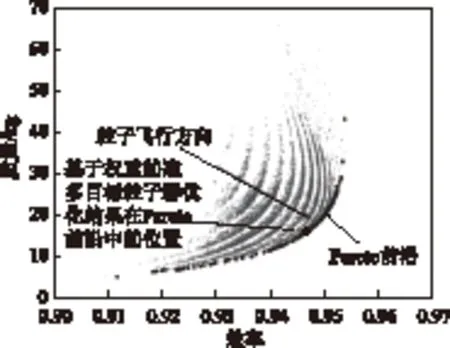
图6 改进多目标粒子群优化结果Fig.6 The optimization results of improved MOPSO
在两个子群中分别取3个粒子,以Ro为例,其收敛过程如图7所示。由图7可看出,粒子经过40代左右趋于收敛,但与准多目标PSO不同的是,最终并不收敛于一个确定的值,而是一个范围。这是因为改进的MOPSO两个子群中始终保持5%的粒子进行变异,引导子群飞向附近新的方向。
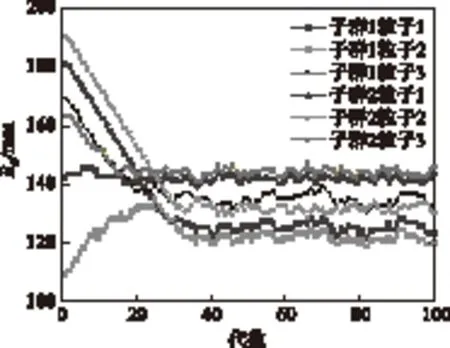
图7 参数Ro收敛过程Fig.7 The convergence process of Ro
将基于改进的MOPSO优化结果同NSGA-Ⅱ多目标优化算法进行比较。其中NSGA-Ⅱ初始种群100个,进化代数100代。两者的Pareto前沿对比如图8所示。由图8看出,改进的多目标粒子群算法所得到的Pareto前沿同NSGA-Ⅱ算法相比较,可在相同质量下获得更高的效率,即得到的Pareto前沿距离实际的Pareto前沿更接近。通过计算两种Pareto前沿的平均间距及归一化欧氏距离,分析其分布性,如表3所示。可看出,改进的MOPSO获得的Pareto前沿平均间隔和归一化欧氏距离均较小,分布性更好。

图8 Pareto前沿集对比Fig.8 The contrast of pareto front set

指标NSGA-ⅡMOPSO平均间距2.91892.1531归一化欧氏距离5.42675.1456Pareto前沿集数量212227
在Pareto前沿中,需要根据实际要求选择最佳方案。本文根据在AUV总体设计时限定的最大质量选取对应的效率,作为最佳设计方案,3种方法的最佳方案如表4所示。由表4可看出,经验权重法未充分利用总体给出的质量要求,而NSGA-Ⅱ法在相同质量要求下得到的电机效率没有改进的MOPSO高。

表4 优化结果Tab.4 Optimization results
3.2 模型验证
电磁-热耦合模型的准确性直接影响优化结果的准确性。通常使用有限元方法对设计结果进行验证,本文使用Magnet软件对电机气隙磁密进行计算对比,图9为空载气隙磁密分布对比。可以看出,解析法与有限元法计算所得的气隙磁密趋于一致,空载每极磁通量磁通误差约为0.4%。

图9 优化电机空载气隙磁密分布Fig.9 No-load magnetic flux distribution of the optimization motor
同样,使用Ansys 软件计算水温为10℃时稳态温度分布,如图10所示。和等效热网络法计算的温升结果对比如表5所示。可看出等效热网络法和有限元法计算的最高温度均出现在绕组处,且温度分布一致,各部分误差在2℃以内。

图10 水池温度为10℃时AUV温度分布Fig.10 Temperature distribution of AUV when the water temperature is 10℃
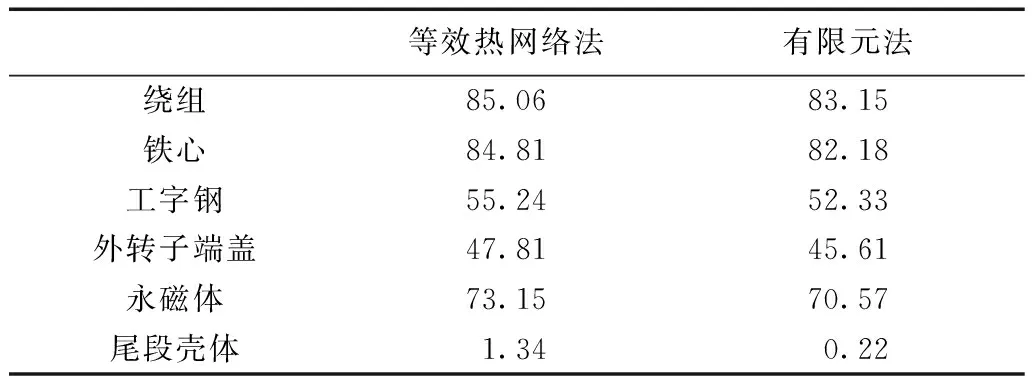
等效热网络法有限元法绕组85.0683.15铁心84.8182.18工字钢55.2452.33外转子端盖47.8145.61永磁体73.1570.57尾段壳体1.340.22
3.3 样机试验
根据MOPSO优化结果制作样机,在实验室加210 V电压,空载转速为1 258 r/min,与本文计算模型相比,空载转速误差为4.8%。将样机安装在尾段舱内,AUV尾段经过舱内加压密封试验后,安装在实验平台上,并全部浸于水池中,通过水下航行器尾段静态负载试验系统检测尾段输出功率。使用K型热电偶测量内转子的温度,热电偶导线连接至温度检测装置,将电压信号转换为数字信号。数字信号通过串行红外信号传送至电机壳体接收端。温度检测装置安装在内轴上未连接螺旋桨的一端,并且与内转子一同旋转。为减小测量误差同时保证转子动平衡,将4个K型热电偶均匀分布贴在绕组端部,测量结果取平均值。动力电池输出电压为210 V,通过电机控制器调节实验转速为1 200 r/min。通过扭矩测试平台得到尾段的推进功率为4.59 kW。对转螺旋桨效率为90%,因此电机输出功率约为5.1 kW。测量电机的输入电压和电流,得到电机的输入功率为5.363 kW,计算得到电机的效率约为95.1%。
实验时水池温度为10.2℃,持续推进5 h。实际测试的满负载瞬态温升曲线如图11所示。可看出电机经过约110 min后温度趋于稳定,端部绕组温度为90.8℃,温升为80.6℃。绕组温升计算误差为4.26℃。这是因为试验测量的是端部绕组温度,而实际上绕组最高温度应在槽内绕组的中间。另外,轴承损耗和端部绕组的长度是基于经验给出的,因此此误差是合理的。

图11 5 h负载实验电机温度测量Fig.11 Motor temperature measuring on 5 hours load
随着水池温度增加,电机的最高温度会随之上升,不同水温下电机的温升如表6所示。

表6 不同水温下电机温升Tab.6 Motor temperature rise at different water temperature
由表6可知,当水池温度升高时,AUV尾段温差基本不变。这是因为热量传递主要和传热介质的热物理性质有关,而水温度变化并未改变这种性质,因此尾段温升及温度分布基本无变化。
4 结论
本文针对某型AUV对推进电机的特殊需求,提出了一种基于电磁-热耦合的子群协同优化的多目标粒子群设计方法。将计算模型与有限元法进行比较,表明计算模型较准确。以质量和效率为优化目标,电机温升和几何条件及磁路磁密为约束条件进行优化。将改进的MOPSO算法与NSGA-Ⅱ算法进行比较。结果表明相对于NSGA-Ⅱ,该方法能够获得距离真实Pareto前沿更近的解集。最后在多目标优化的前沿集中选取最终方案,试制样机后进行水下航行器尾段静态负载实验,且尾段密闭条件下5 h负载温升达到要求。
[1] 宋受俊,葛乐飞,刘虎成,等.开关磁阻电机设计及多目标优化方法[J].电工技术学报,2014,29(5):1-9. Song Shoujun,Ge Lefei,Liu Hucheng,et al.Design and multi-objective optimization method of switched reluctance machines[J].Transaction of China Electrotechnical Society,2014,29(5):1-9.
[2] Upadhyay P R,Rajagopal K R.Genetic algorithm based design optimization of a permanent magnet brushless DC motor[J].Journal of Applied Physics,2005,97(10):(10Q516-10Q516-3).
[3] 褚占宇,安忠良,佟文明,等.双转子永磁风力发电机设计[J].电工技术学报,2013,28(1):265-270. Chu Zhanyu,An Zhongliang,Tong Wenming,et al.Design and research on dual-rotor permanent-magnet wind generator[J].Transaction of china electrotechnical society,2013,28(1):265-270.
[4] 张晓锋,梁京辉,乔鸣忠,等.机桨一体化推进电机设计及分析[J].电工技术学报,2013,28(11):170-175. Zhang Xiaofeng,Liang Jinghui,Qiao Mingzhong,et al.Design and analysis of propelling motor used in a integrated motor propulsor[J].Transaction of china electrotechnical society,2013,28(11):170-175.
[5] Hwang C C,Chang J J.Design and analysis of a high power density and high efficiency permanent magnet DC motor[J].Journal of Magnetism and Magnetic Materials,2000,209(1-3):234-236.
[6] Yang Y P,Chiao T C.Multi-objective optimal design of a high speed brushless DC motor[J].Electric Machines and Power Systems,2000,28(1):13-30.
[7] Zhu Z Q,Howe David,Chan C C.Improved analytical model for predicting the magnetic field distribution in brushless permanent-magnet machines[J].IEEE Transactions on Magnetic,2002,38(1):229-238.
[8] Rahideh A,Korakianitis T,Ruiz P,et al.Optimal brushless DC motor design using genetic algorithms[J].Journal of Magnetism and Magnetic Materials,2010,322(22):3680-3687.
[9] Mellor P H,Roberts D,Turner D R.Lumped parameter thermal model for electrical machines of TEFC design[C].IEE Proceedings Electric Power Applications,1991,5(138):205-218.
[10]Howey David A,Childs Peter R N,Holmes Andrew S.Air-gap convection in rotating electrical machines[J].IEEE Transactions on Industrial Electronics,2012,3(59):1367-1375.
[11]Parsopoulos K E,Vrahatis M N.Particle swarm optimization method in multi-objective problems[C].Proceedings of the 2002 ACM Symposium on Applied Computing,Madrid,Spain,2002,603-607.
Optimization Design of An AUV’s Motor with Counter-rotating Rotors Based on the Collaborative Multi-objective Particle Swarm Algorithm
WangSiling1SongBaowei1DuanGuilin2
(1.College of Marine Engineering Northwestern Polytechnical University Xi’an 710072 China 2.China Shipbuilding Industry Corporation 710 Yichang 443003 China)
An autonomous underwater vehicle (AUV) in design requires a new motor with counter-rotating rotors which should have a high efficiency and a small mass,and can be operated for a relatively long time in a closed space where the temperature rise must be considered.An electromagnetic-thermal coupling analysis model and an improved multi-objective particle swarm optimization (MOPSO) algorithm based on the Pareto optimal are used for the design of the motor.Firstly,an analytical model is applied for the calculation of the air gap magnetic field,an equivalent thermal network analysis is used to calculate the motor’s temperature rise,and the interaction between the electromagnetic field and the thermal field is considered.Secondly,the computational fluid dynamics (CFD) method is used for calculating the convection heat transfer coefficient of the rotating parts of the motor and the AUV shell to solve the problem of the inaccurate equivalent thermal resistance.Finally,the efficiency and the mass are set as the optimization objectives,the temperature rise and the geometric condition are designated as the constrains.Then the results of a two sub-groups collaborative MOPSO algorithm is compared with the results of the standard multi-objective optimization algorithm NSGA-Ⅱ.The Pareto front shows that the method can obtain a solution set that is closer to the true Pareto front with good distribution.The experimental results of the prototype show that all the indices including power,speed,efficiency and mass meet the requirements,and the temperature rise after 5 hours’ full-load is satisfied.
Autonomous underwater vehicle,counter-rotating rotors motor,multi-objective optimization,particle swarm,thermal-electrical coupling,computational fluid dynamics
2014-11-27 改稿日期2015- 01- 06
TM315
王司令 男,1985年生,博士研究生,研究方向水下航行器电机设计与控制。(通信作者)
宋保维 男,1963年生,教授,博士生导师,研究方向为水下航行器总体技术。
总装预研项目(401030201)资助。

