盾构隧道注浆抬升施工对衬砌结构的影响

赵 欣

(湖南交通职业技术学院 长沙 410132)

盾构隧道注浆抬升施工对衬砌结构的影响

赵 欣

(湖南交通职业技术学院 长沙 410132)

基于盾构隧道注浆抬升工程，建立盾构隧道注浆抬升对管片衬砌结构影响计算模型，通过对比现场实测数据和数值计算结果，验证计算模型的正确性；在此基础上探讨分析不同注浆位置、不同注浆顺序对管片衬砌结构的影响，为盾构隧道注浆抬升施工提供参考依据。

盾构隧道注浆抬升；计算模型；不同注浆位置；不同注浆顺序；管片；衬砌结构

1 盾构隧道注浆抬升技术研究现状

本文根据上海市某工程盾构隧道结构注浆抬升工程现场实测数据，验证隧道结构注浆抬升计算模型的正确性；在此基础上探讨不同注浆位置、不同注浆顺序对衬砌管片结构内力的影响，为盾构隧道注浆抬升的施工提供参考依据。

2 数值模拟计算

2.1 模型建立及参数取值

上海市某工程盾构隧道管片外径为6.2 m，内径5.5 m，混凝土强度为C50，采用螺栓强度等级为5.8级的弯螺栓拼接而成；隧道顶覆土11.48 m，地下水位埋深0.6～2.2 m。在注浆过程中为了提高隧道的整体性，减少隧道变形，要在隧道注浆各环内架设支撑。

采用有限元软件Plaxis2D建立计算模型，其中隧道左右两侧边缘距离隧道中心50 m，大于3倍隧道直径，以便忽略边界影响。土体采用摩尔库伦本构模型，具体土层物理力学性质参数如表1所示，模型中土层分布如图1(a)所示。隧道结构假定为均质圆环，采用板壳单元模拟，刚度折减系数取为0.75，根据实际支撑布置情况在隧道内增加支撑，隧道中部支撑用杆单元模拟，结构参数如表2所示。对衬砌管片K8、K10两注浆孔下方土体进行注浆，如图1(b)所示，图中隧道下方红色单元为注浆单元。邓指军等研究了盾构隧道微扰动注浆过程中的注浆参数[12]，通过对比计算地层和上海试验地层的土体性质、注浆深度、浆液配比等参数，发现注浆加固后土体刚度及强度参数对注浆抬升过程和结构内力的影响不大，土体膨胀法模拟隧道注浆抬升，隧道结构内力主要与下方注浆单元体应变有关。因此，根据上海地区试验选取的注浆后土体刚度及强度参数较为合理。

表1 土层物理力学性质指标

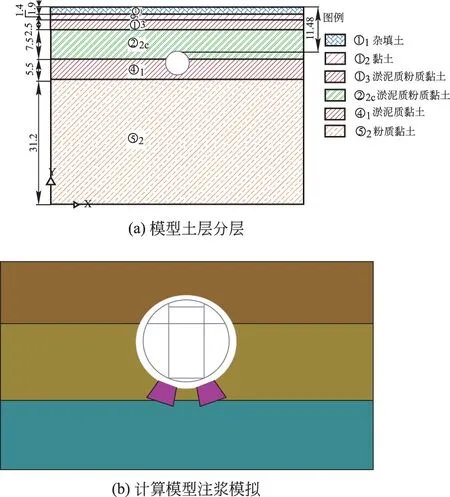
图1 数值计算模型

结构名称单元类型EI/(kN·m2/m)EA/(kN/m)泊松比v隧道管片板壳单元9.24×1041.21×1070.15竖向支撑杆单元—8.65×1050.30横向支撑杆单元—2.95×1050.30

2.2 数值计算步骤

1) 建立几何计算模型；

2) 划分网格，隧道附近细化网格并设置各材料的模型参数;

3) 施加初始条件并约束左、右两边及底部对应方向的位移：施加重力场，计算初始有效应力，并将各方向位移归零；

4) 关闭衬砌内的土体对应单元，激活钢支撑对应单元，同时激活衬砌单元生成土体与衬砌的接触作用；

5) 根据隧道注浆抬升不同工况进行计算，输出变形和应力云图以及特征节点的计算数据。

模拟隧道注浆抬升时，通过对注浆单元(即代表注浆土体的单元)施加体应变使单元体积膨胀来模拟抬升过程，包括2个步骤：增加注浆区域的土体刚度和强度；施加各向大小相同的体应变。在数值模拟过程中，通过判断隧道抬升量是否达到实际隧道抬升量来控制模拟注浆过程，具体流程如图2所示。

图2 数值模拟流程

2.3 数值计算与实测数据对比数值计算与现场实测的地表隆沉计算结果、隧道内支撑轴力及水平直径收敛变形对比如表3所示。

表3 数值计算与现场实测数据对比

由表3可知，数值计算所得结果与实测数据存在误差。在实际注浆过程中，168、169环隧道的两侧支撑轴力相差较大，且隧道发生了较大的横向收敛变形，这是由于隧道支撑特别是右侧支撑在架设时未和隧道管片结构紧密贴合，造成隧道的变形较大。通过数值计算方法研究注浆抬升对隧道管片的影响是可行的。

3 不同注浆抬升工况对衬砌结构的影响

3.1 隧道内部支撑对注浆抬升时衬砌结构的影响研究单环管片内部支撑体系对结构内力的影响。注浆后土体参数及其他假设与2.1相同，分别模拟隧道在有、无支撑情况下注浆抬升10、20、30、40、50 mm的情形。

结构内力计算结果如图3所示：在隧道抬升量10～50 mm时，无支撑情况管片的最大弯矩、最大弯矩处轴力均大于有支撑情况管片的对应值，当抬升量为50 mm时，无支撑情况管片的最大弯矩比有支撑的情况大132.9%；无支撑情况管片的水平收敛变形量约是有支撑情况的4～10倍；根据对最大弯矩处截面进行裂缝宽度验算，在有支撑情况下的截面裂缝宽度发展缓慢，无支撑情况下截面裂缝宽度发展较迅速，当抬升量为50 mm时，无支撑情况的裂缝宽度已接近有支撑情况的5.4倍。

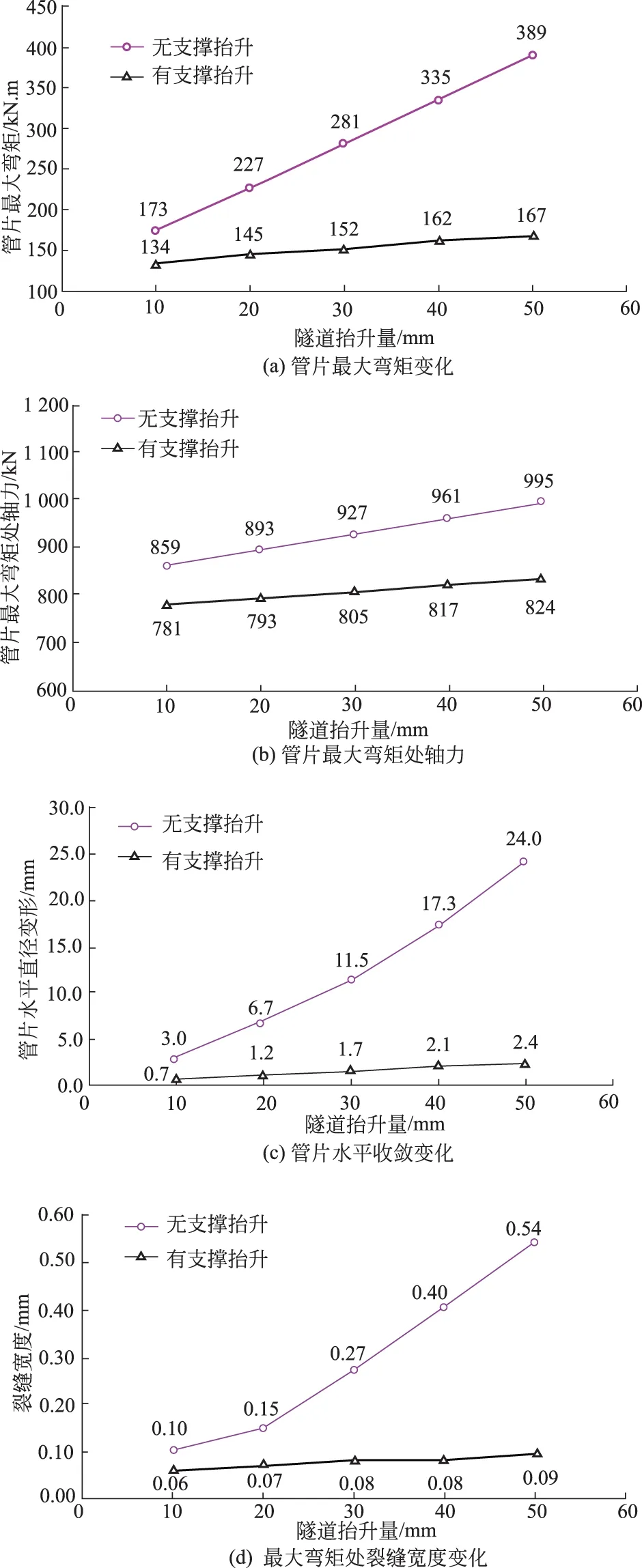
图3 隧道内部有无支撑注浆抬升对结构的影响

注浆抬升施工后待支撑轴力及隧道变形收敛值保持稳定后，需进行拆撑(拆除支撑)。通过现场监测发现支撑拆除后支撑轴力、变形收敛基本保持平稳，说明注浆起到了预期的效果，能够有效增强侧向土体强度以及土体抗力，从而控制隧道在拆除支撑后应力释放过程中的变形；同时部分支撑在隧道抬升期间发生了塑性变形，从而在一定程度上保证了隧道的过量收敛变形。

3.2 不同注浆位置及顺序对衬砌结构的影响

3.2.1 不同注浆位置对衬砌结构的影响

对比两边注浆(K8、K10两孔)与中间注浆(K9单孔)，研究单环管片注浆位置对隧道结构内力的影响。假定两边注浆时左右两侧注浆量相同，注浆深度为1.50 m，注浆后土体参数及其他假设与2.1相同。分别模拟单环管片在隧底不同范围注浆抬升10、20、30、40、50 mm的情况。

隧道结构内力计算结果如图4所示。隧道注浆抬升相同高度时，采用中间注浆比两边注浆的隧道内支撑轴力大，二者差值随着隧道注浆抬升量的增大而增大，其中隧道抬升50 mm时，采用中间注浆比两边注浆的隧道内支撑轴力大36.5%；采用中间注浆比两边注浆的隧道管片最大弯矩大，二者差值随着隧道注浆抬升量的增大而逐渐增大，当隧道抬升50 mm时，中间注浆比两边注浆的管片最大弯矩大137.3%；采用中间注浆管片的最大弯矩处的裂缝宽度远大于两边注浆的情况，当隧道抬升50 mm时，采用中间注浆管片最大弯矩处的裂缝宽度是两边注浆的6倍。通过对比发现，采用两边(K8、K10注浆孔)注浆相比中间(K9注浆孔)注浆，对隧道结构内力的影响更小。

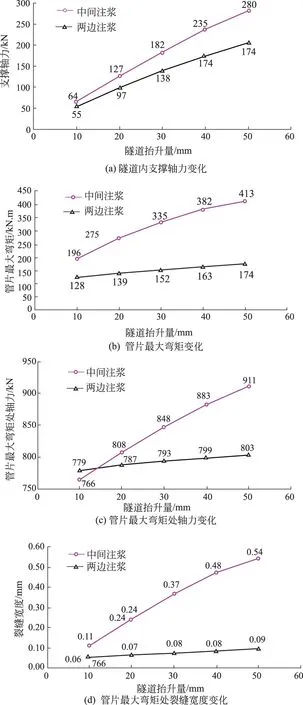
图4 不同注浆位置对隧道结构的影响

3.2.2 深度方向不同注浆顺序对衬砌结构的影响

对比K8、K10两注浆孔采用自上而下与自下而上两种注浆顺序，研究单环管片深度方向不同注浆顺序对隧道结构内力的影响，注浆顺序如图5所示。注浆深度为1.50 m，分10层(每层0.15 m)逐层等量注浆。

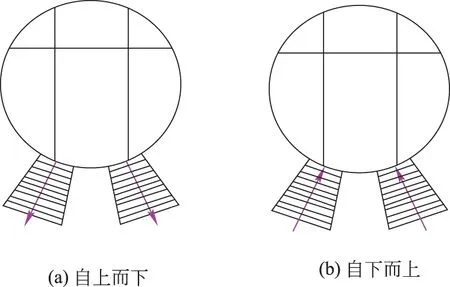
图5 深度方向不同的注浆顺序

隧道结构内力计算结果如图6所示。隧道注浆抬升相同高度时，采用自下而上注浆比自上而下注浆的隧道内支撑轴力大，二者差值随着隧道注浆抬升量的增大而增大，当隧道抬升50 mm时，自下而上注浆比自上而下注浆的隧道内支撑轴力大14.5%；采用自下而上注浆比自上而下注浆的隧道管片结构最大弯矩大，当隧道抬升50 mm时，自下而上注浆比自上而下注浆的隧道最大弯矩大8.5%；采用自下而上注浆与自上而下注浆相比，管片的最大弯矩处裂缝宽度差别不大。

图6 深度方向不同注浆顺序对结构的影响

将不同注浆顺序等抬升量模拟改为不同注浆顺序等注浆量(体应变)模拟，分别模拟深度及方向不同的注浆顺序，注浆单元体应变为8.5%、10.0%、11.5%时的隧道抬升情况，模拟结果如图7所示。

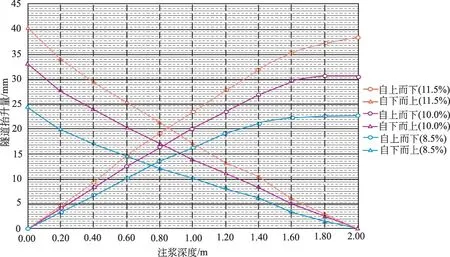
图7 隧道抬升量随注浆深度变化

在0～2.0 m范围内注浆时，采用自下而上注浆，因为下方1.8 m范围内凝固的浆液为上部注浆提供了更好的持力层，所以在注浆量相同的情况下，采用自下而上顺序注浆比自上而下顺序注浆，隧道的抬升量更大。采用自上而下的注浆顺序，当注浆深度超过1.6 m时，上部浆液凝固对下部注浆的阻隔作用逐渐增大，注浆对隧道抬升的影响逐渐减小，表现为曲线斜率逐渐降低，尤其当注浆量不大时，在1.8～2.0 m范围内注浆对隧道抬升已基本无影响。因此，需根据隧道所需抬升量，结合具体地层情况选择合适的注浆深度。

3.2.3 注浆不同先后顺序对衬砌结构的影响

对比先中间(K9)后两边注浆(K8、K10)与先两边(K8、K10)后中间注浆(K9)的两种顺序注浆，研究单环管片水平方向注浆顺序对隧道结构内力的影响。

注浆顺序如图8所示，注浆深度为1.50 m，假定3个注浆孔注浆量相等，注浆后土体参数及其他假设与2.1章节相同，分别模拟隧道以水平方向不同顺序注浆抬升10、20、30、40、50 mm的情况。

图8 不同注浆顺序

隧道结构内力计算结果如图9所示。隧道注浆抬升相同高度时，采用先两边后中间注浆比先中间后两边注浆的隧道内支撑轴力大，二者差值随着隧道注浆抬升量的增大而增大，当隧道抬升50 mm时，先两边后中间注浆比先中间后两边注浆比隧道内支撑轴力大10.5%；采用先两边后中间注浆比先中间后两边注浆的隧道管片最大弯矩大，二者差值随着隧道注浆抬升量的增大而增大，当隧道抬升50 mm时，先两边后中间注浆比先中间后两边注浆的隧道最大弯矩大32.1%；先两边后中间注浆比先中间后两边注浆的管片裂缝宽度增长更快，在隧道抬升50 mm时，先两边后中间注浆的管片最大弯矩处裂缝宽度是先中间后两边注浆的2倍。因此，需要对隧道底部3个注浆孔注浆时，采用先中间后两边的顺序注浆，对隧道结构内力的影响更小。

图9 注浆不同先后顺序对结构的影响

4 结论

对盾构隧道注浆抬升不同工况进行数值模拟，计算了不同注浆位置及顺序时，使隧道抬升至相同高度时的结构内力、变形的变化规律，得到以下结论：

1) 在注浆过程中通过在隧道架设支撑可有效减小结构内力。

2) 在抬升量相同的情况下，仅两侧注浆情况引起的结构内力值明显小于仅隧底注浆的情况。

3) 深度方向的注浆顺序不同，隧道结构内力、变形也不同。

4) 采用自上而下注浆时，上部浆液凝固对下部注浆有一定的阻隔作用，当注浆深度超过一定范围后，继续注浆对隧道抬升基本无影响。

5) 如注浆范围一定而注浆顺序不同时，结构内力也不同。

6) 以隧道抬升量相同、结构内力最小为控制标准，建议采用“自上而下，先中间后两边，中间加固两边抬升”的注浆抬升方法，并尽量加大注浆范围。

[4] 李军.注浆加固技术在地铁隧道结构沉降处理中的应用研究[D].广州:华南理工大学,2013.

[10] 蔡军.隧道穿越建筑物过程中注浆抬升技术研究[D].北京:北京交通大学,2009.

[11] 董葳.注浆抬升的数值模拟及抬升规律研究[D].北京:北京交通大学,2014.

(编辑：郝京红)

Influence on Lining Structure by Grouting Uplift of Shield Tunnel

Zhao Xin

(Hunan Communication Polytechnic, Changsha 410132)

Based on a grouting uplift project of shield tunnel, the influence calculation model of shield tunnel uplift grouting on segment lining structure is established. The calculation model is verified to be correct by comparing the measured on-site data and the numerical results, and the influence of different grouting positions, different grouting orders on the segment lining structure is discussed, which provides theoretical reference for shield tunnel grouting uplift projects.

grouting uplift of shield tunnel; calculation model; different grouting position; different grouting order; shield segment; lining structure

赵欣，男，硕士，讲师，从事轨道交通安全及测绘测量的研究，zhlwtg@163.com

U456.3

A