基于熵权TOPSIS的轨道交通线网分级测度

戢小辉 张 磊 金 键 沈 犁

(1. 西南交通大学交通运输与物流学院 成都 610031;2. 广州铁路(集团)公司安全监察室 广州 510088)

戢小辉1张 磊2金 键1沈 犁1

(1. 西南交通大学交通运输与物流学院 成都 610031;2. 广州铁路(集团)公司安全监察室 广州 510088)

轨道交通；熵权法；TOPSIS模型；分级测度

1 轨道交通线网分级测度简介

目前，在众多评价模型中，应用于轨道交通线网评价的主要模型有层次分析法[4]、模糊数学评价法[5]、物元分析法[6]、灰色关联度法[7]、逼近理想解算法[8]5种以及它们的组合，其中层次分析法因其思路清晰、计算简捷最为常用。

这5类模型虽各具特点，能从不同角度对轨道交通线网进行分级测度，但经过详细分析发现，这5类模型都存在诸多不足:1)层次分析法中的指标权重因受专家主观选择偏好影响，在数理逻辑层面缺乏一定说服力;2)当指标集较大时，模糊数学法相对隶属度权重系数会偏小，导致权向量与模糊矩阵不匹配，使结果出现超模糊现象;3)物元分析法中也存在指标权重取值的主观性，尽管可以通过熵权法解决，但是其经典域和节域的确定仍缺乏有效的依据;4)灰色关联法中分辨率的取值缺乏合理标准，一旦标准选择失误，会导致灰色关联系数计算结果放大失真;5)逼近理想解算法中决策矩阵没有分析各评价指标的权重差异。

2 模型建立

2.1 熵权法

申农(C.E.Shannon)于1948年将热力学中的熵概念引入信息论，称为信息熵。按照信息论中解释：信息熵是表征一个系统有序程度的量，一个系统有序程度越高，信息熵越大；一个系统的无序程度越高，信息熵越小。根据这一原理，引入一种客观赋权法，即根据自身评价指标值来确定权重的熵权法，该方法能通过各指标的变异程度，根据信息熵测算各个评价指标的熵权，再通过熵权结合客观要求对各指标的权重进行修正，进而得到各指标的评价权重。通常来说，信息熵越小，表征评价指标的差异程度越大，即该指标提供的信息量越大，权重越大。利用熵值法计算轨道交通线网分级指标权重的步骤如下。

1) 将m个预选方案和n个评价指标值的原始数据Xij(i=1,2…,m;j=1,2…,n)组成的矩阵定义为X。

2) 将指标数据标准化

(1)

3) 测算指标信息熵

(2)

信息偏差度dj为

dj=1-Ej

(3)

4) 熵权测算

(4)

(5)

2.2 TOPSIS模型

TOPSIS(technique for order preference by similarity to ideal solution)通常被称为逼近于理想值的排序方法，它是Hwang和Yoon于1981年提出的一种适用于有限方案多目标决策的综合评价方法。该方法具有如下优点：利用原始统计数据信息反应方案差距；对样本数据资料要求简洁方便；测算结果真实、直观、可靠；较单项指标相互分析法，能集中反映总体情况及综合分析评价，具有普遍适用性。故其目前已在公共事业管理、项目风险评价、方案比选、宏观经济效益评价等多个领域受到广泛应用。该方法的核心思想是定义决策问题指标集的理想解和负理想解。理想解是设想的最优解，其属性值是所有预选方案中最好的；负理想解是设想的最差解，其属性值是所有预选方案中最差的。为了在所有预选方案中找到一个方案，使其与理想解的距离最近，而与负理想解的距离最远，需要测算待评价的各个方案到理想值和负理想值之间的加权欧式距离，进而得出各预选方案与最优方案的接近程度，以此为评价方案优劣的标准。计算步骤如下。

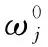
(6)

2) 筛选理想解和负理想解。令A+表示最偏好的方案，A-表示最不偏好的方案，通常成本型指标和效益性指标选择方法不同，笔者所用的方案为

(7)

(8)

3) 测算各个预选方案到理想解和负理想解的欧式加权距离

(9)

(10)

式中,a+j和a-j分别为集合A+和A-中的元素。

4) 测算预选方案与理想解的贴近度

(11)

将c+i由大到小进行降序排列，最大的c+i对应的预选方案为最优方案，最小的c+i对应的预选方案为最差方案。

3 算例分析

3.1 指标构建

轨道交通线网评价是明显的多目标决策问题，构建其评价指标体系，关键是完成影响因素的机理分析。由于城市轨道交通项目是一项长期、复杂的系统工程，影响其线网分级水平的因素众多，目前工程界和学界都尚无一套公认的评价指标体系。成都和昆明从城市发展战略、线网结构、客运效果、社会效益和可实施性角度出发，构建如图1所示的评价体系。

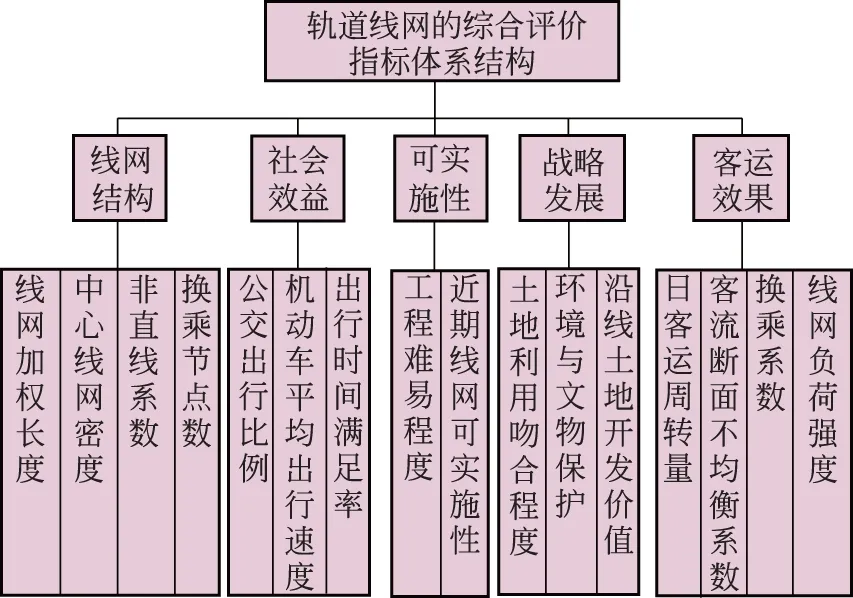
图1 成都和昆明轨道交通线网评价指标体系

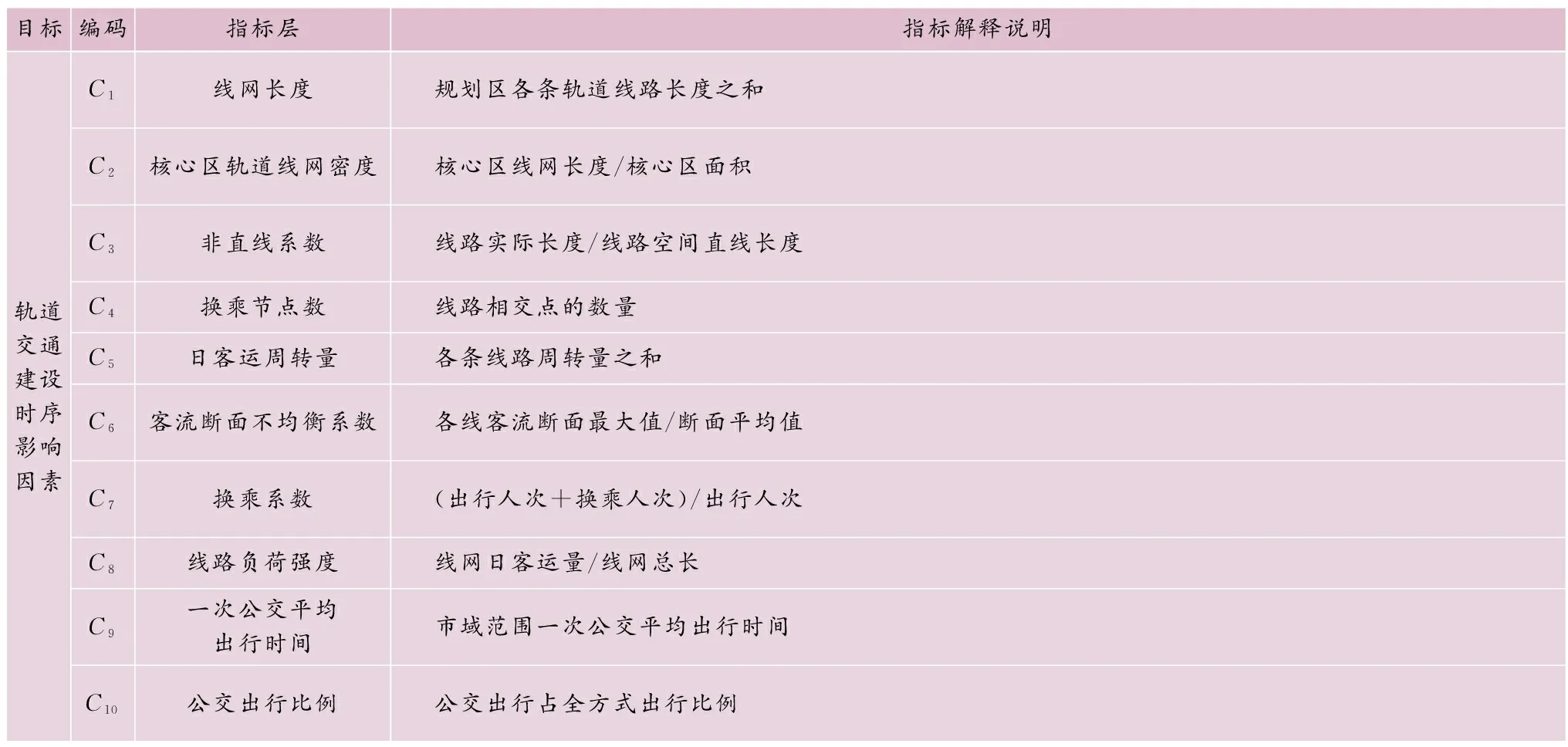
表1 城市轨道交通综合测评指标

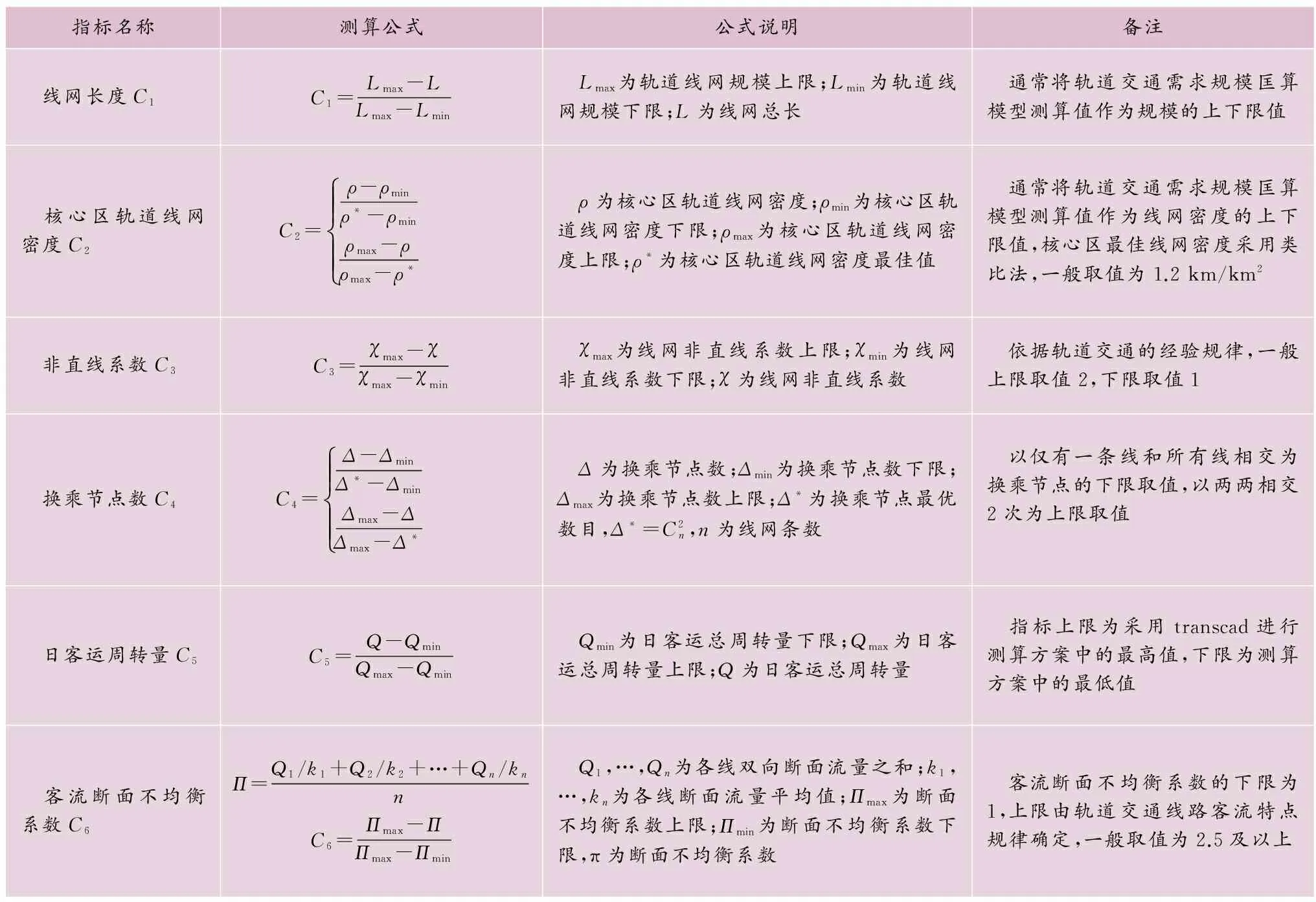
表2 评价指标测算处理

续表

表3 4个方案的评价指标统计值与处理值

3.3 熵值法计算权重将表3中4个预选方案的所有指标的理论值构造成目标矩阵X,再由式(1)得到标准化矩阵Pij

由式(2)计算得到每个评价指标的熵值为

Ej=(0.000 748,0.001 141,0.001 033,0.001 084,0.000 626,0.000 447,0.000 317,0.001 055,0.000 543,0.000 667)

由式(3)～(5)得到各指标熵权为

ωj=(0.10,0.15,0.13,0.14,0.08,0.06,0.04,0.14,0.07,0.09)

由于原始统计数据方案间差距表征性不强，故运用表1中的测算公式，将所有指标进行相应的规范化处理，得到表3中的指标得分值。将该得分值与利用熵权法得到的权重向量进行加权化处理，并利用公式(6)得到相应的加权化标准决策矩阵Z。

利用公式(7)、(8)筛选得到表征方案优劣的理想解和负理想解。

利用公式(9)、(10)分别计算4个预选方案得到理想解A+和负理想解A-之间的欧式几何距离d+和d-，计算结果如下

利用公式(11)，分别测算得到的4个预选方案与理想解的贴近度，见表4。

表4 贴近度计算结果

测算结果表明： C+2>C+3>C+1>C+4,即最终的方案分级结果为方案2最优，方案3、方案1次之，方案4最差。将测算结果与AHP测算结果对比分析还可以看出:两种方法对轨道交通预选方案的分级测算评估结果是基本相同的，恰好验证了模型的可靠性。

4 结论

2) 对成都的4个远景轨道交通预选方案进行实例分析，结果显示4个预选方案的贴近度值分别为0.489 21，0.857 16，0.702 79，0.262 26，即方案2最优，方案3、方案1次之，方案4最差，其中方案2与目前成都主推线网走向基本一致，从侧面验证了模型的合理性和有效性。

3) 根据不同城市、不同时期的准确交通需求数据进行指标上下限取值，提高测算模型精度是下一步需要继续探讨的课题。

(编辑：王艳菊)

Grading Evaluation Model of Urban Rail Transit Network Based on Entropy TOPSIS

Ji Xiaohui1Zhang Lei2Jin Jian1Shen Li1

(1.School of Traffic & Logistics, Southwest Jiaotong University, Chengdu 610031;2.Security Supervising Department, Guangzhou Railway (Group) Corp., Guangzhou 510088)

It is very difficult, subjective and sensitive in determining the index weights of the conventional grading evaluation model. To avoid these problems, entropy weight method was adopted to build a comprehensive evaluation model for rail transit network. On the basis of the properties of urban rail transit network, the paper presented the evaluation index system and the equations to get the indexes which were calculated objectively from original data. Then the entropy TOPSIS evaluation model was built and verified in appraising the prospective preliminary programs of Chengdu urban rail transit. The simulation results which were applicable in making comprehensive decisions for rail transit network demonstrated the scientific validity and feasibility of this approach.

urban rail transit; entropy weight method; TOPSIS model; grade evaluation

戢小辉，男，硕士，主要研究城市轨道交通规划与客流预测，947683336@qq.com

国家自然科学基金项目(51108390)

U231.2

A