CGCS2000与独立坐标系转换模型适用性研究
李 东,毛之琳,廖文兵,陈 敏
(国家测绘地理信息局 大地测量数据处理中心,陕西 西安,710054)
国家参心坐标系控制网受当时科技水平限制,大地控制点的相对精度为10-6,而 CGCS2000[1]控制网采用GPS方法施测,大地控制点的相对精度为10-7~10-8[2]。而大多数城市独立坐标系是基于国家参心坐标系控制点建立的,其控制网建立方法与国家参心坐标系控制网基本相同,其精度也基本相同。CGCS2000与城市独立坐标系相互转换,由于两者精度不同,对转换产生的坐标(简称:转换坐标)有不同的要求:①当CGCS2000向城市独立坐标系转换时,有需要尽可能与原独立坐标符合;又有需要尽可能保持CGCS2000成果高精度。但是,如果转换坐标与原独立坐标具有高符合性,两者精度必然接近,也就不可能保持CGCS2000成果的高精度。反之,保持了高精度,必然与原独立坐标符合的较差。②当城市独立坐标系向CGCS2000转换,属于低精度成果向高精度转换,通常要求转换坐标尽可能与CGCS2000坐标符合。采用重合点和模型进行坐标转换时,当重合点精度和数量满足条件前提下,转换坐标特性可通过不同模型来反映,如何根据需要选择最佳转换模型,又如何通过某种方法来检验模型所具有特性等问题。本文提出利用CGCS2000与城市独立坐标系的边长差和方位角差,对常用转换模型进行比较 根据其变化量大小和变化趋势,分析转换模型特性,并用同一地区两期GPS数据进行验证,通过图表反映出转换模型的特性。
1 常用坐标转换数学模型
1.1 Bursa(三维七参数)模型

其中,3个平移参数 [ΔX ΔY ΔZ]T,3个旋转参数 [ωXωYωZ]T和 1 个 尺 度 因 子 m。[XNYNZN]为目标坐标系坐标。
1.2 多项式(多元逐步回归)模型

式中:BT,LT分别为目标坐标系大地坐标;BS,LS分别为源坐标系大地坐标;ΔB,ΔL分别为坐标转换改正量,用下式计算:
ΔB或ΔL=a1+a2B+a3L+a4B2+a5BL+a6L2+…+a20BL4+a21L5.
其中:a1,a2,a3,a4,a5,a6… 为系数,通过最小二乘求解。
1.3 平面四参数模型
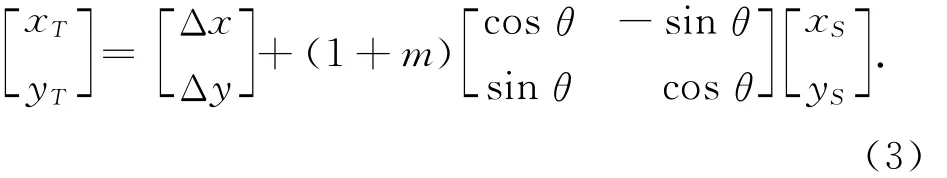
式中:xT,yT为目标坐标系高斯平面坐标;xS,yS为源坐标系高斯平面坐标;Δx,Δy为平移参数;θ为旋转参数;m为尺度参数。
1.4 二维七参数模型
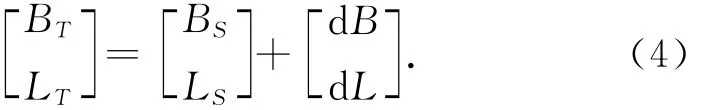
式中:BT,LT分别为目标坐标系大地坐标;BS,LS分别为源坐标系大地坐标;d B,d L分别为坐标改正量,用下式计算:
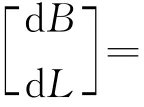

其中:e2,M,N为源坐标系椭球第一偏心率、子午圈曲率半径、卯酉圈曲率半径;d a,d f为源坐标系椭球与目标坐标系椭球长半径差、扁率差;3个平移参数[ΔX ΔY ΔZ]T,3个旋转参数[εXεYεZ]T和1个尺度参数m。
2 检验转换模型特性方法
2.1 利用边长差和方位角差检验转换模型特性
以高精度CGCS2000坐标计算平面边长和方位角作为参照值,将独立坐标系的边长和方位角与其比较,通过变化量大小反映模型的特性。对于城市范围而言,当转换坐标与CGCS2000坐标具有相同精度时,其平面边长差和方位角差极小,接近一个常数。具体是以边长差和方位角差的最大相差和振幅来反映转换坐标特性。最大相差是指最大边长差与最小边长差之差,反映最大波动差;振幅是指离开平均值位置的最大距离边长差。由于边长差与距离成正比,为了统一衡量标准,以每千米边长差作为衡量单位。方位角差的衡量方法类似[7]。公式如下:
边长差最大相差
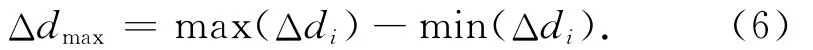
边长差振幅

其中,边长差Δdi= (d2k-d独)×1000/d2k。
方位角差最大相差
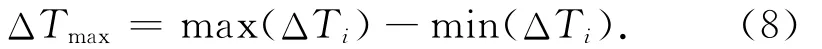
方位角差振幅

其中,方位角差ΔTi=T2k-T独
2.2 用GPS控制网数据验证转换坐标特性
利用同一地区、不同时期两次GPS控制网数据,通过CGCS2000与城市独立坐标系转换,验证转换坐标特性。两次转换选取的重合点及坐标各不同,第一次独立坐标系选用低精度三角测量坐标,第二次选用第一次产生的转换坐标。当高精度成果向低精度转换,如果转换坐标具有高精度,第二次转换为两个高精度坐标之间进行,产生转换坐标为高精度,具体表现为转换残差较小,转换前后形成的边长差和方位角差极为接近。否则,转换坐标为低精度。
3 实例分析
某城市独立坐标系是基于克拉索夫斯基椭球建立的,投影在参考椭球面上,早期城市基础控制网是以三角测量方法布设,2001年和2008年先后布设GPS控制网对原控制网进行改造,两次平差CGCS2000成果的水平方向精度分别为1 c m和0.3 c m。两期坐标转换采用不同的重合点,2001年为7个点;2008年10个点,且独立坐标为2001年转换产生的坐标,见图1。
3.1 坐标转换
以相同模型分别对两期数据进行坐标转换,转换残差见表1。
3.2 2001年CGCS2000向独立坐标转换比较

图1 两次转换重合点分布图

表1 CGCS2000向独立坐标系转换平面坐标残差 m
重合点转换前后独立坐标系边长和方位角与CGCS2000比较,各模型结果见表2,边长差和方位角差波动最小的依次是四参数、Bursa、二维七参、多项式。选择有代表性的多项式和Bursa模型数据,绘制边长差图2和方位角差图3,其中Bursa的边长差及方位角差数值相近,呈一条直线,说明成果保持高精度;而多项式模型转换前后边长差及方位角差数值较相近,图形走势相似,说明保持转换三角测量成果特性,具有较高符合性。

表2 2001年CGCS2000向独立坐标转换边长差和方位角差

图2 2001年CGCS2000向独立坐标系转换边长差图
3.3 2008年CGCS2000向独立坐标转换比较
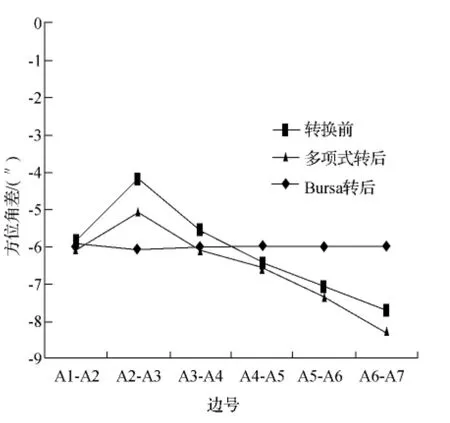
图3 2001年CGCS2000向独立坐标系转换方位角差图
2008年转换的比较结果见表3、图4和图5。Bursa模型转换前后边长差和方位角差极为接近,比2001年结果小一个数量级,反映到图形上,两条线基本合二为一呈水平形状,另外转换残差较小,说明2008年转换属于两个高精度坐标之间的转换,转换坐标具有高符合性,另外说明2001年高精度成果向低精度成果转换,形成转换坐标具有高精度。

表3 CGCS2000向独立坐标系转换边长差及方位角差
如果仅从表1转换残差分析,多项式模型转换精度比Bursa高,但从表3、图4和图5比较,2001年转换前后边长差和方位角差图形走势是基本一致,说明转换成果的符合性较好。虽然先后两次转换残差变小,但边长差、方位角差数量级没变,说明仅提高的是符合性。
3.4 2001年独立坐标向CGCS2000转换比较
独立坐标向CGCS2000转换,为三角测量低精度成果向GPS高精度成果转换,各模型边长和方位角比较结果见表4,其中多项式模型波动最小,其转换成果与CGCS2000成果数值最相近,说明符合性相对最好。

图4 2008年CGCS2000向独立坐标系转换边长差图
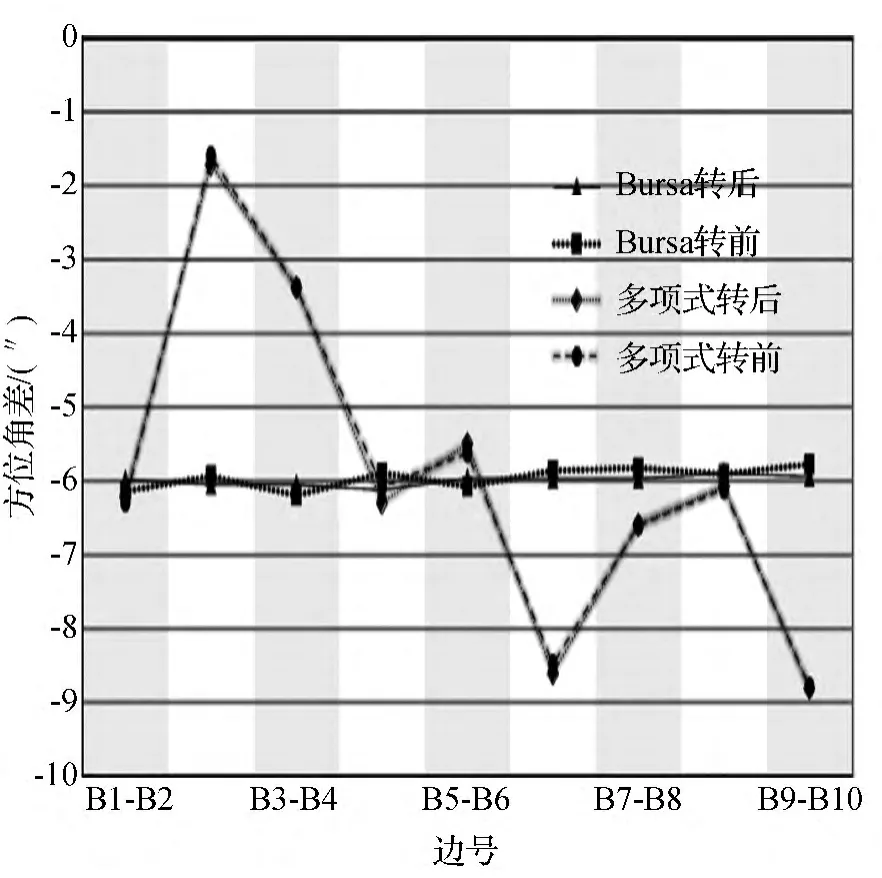
图5 2008年CGCS2000向独立坐标系转换方位角差图
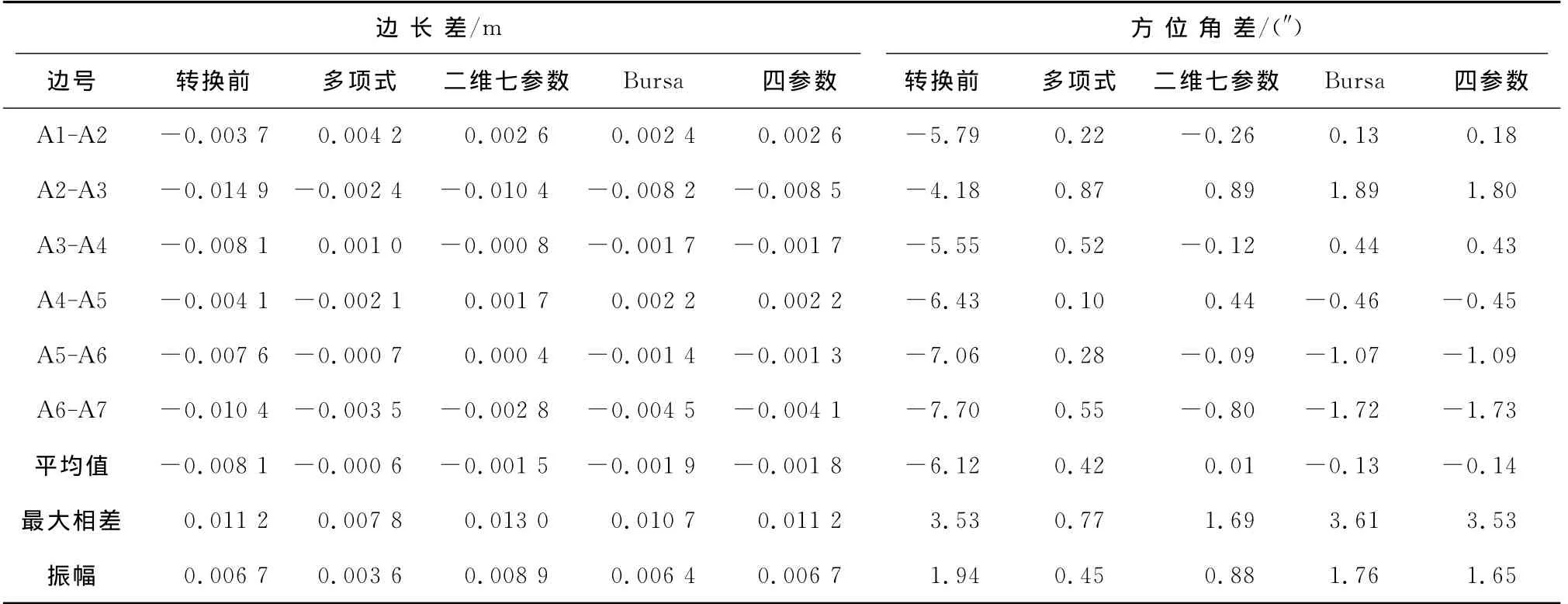
表4 2001年独立坐标向CGCS2000转换前后边长差和方位角差
4 结束语
CGCS2000与城市独立坐标系转换,归纳出常用模型适应性如下:
1)当高精度成果向低精度成果转换,平面四参数或Bursa模型产生转换坐标具有高精度;而多项式模型产生转换坐标具有相对较好符合性。
2)当低精度成果向高精度成果转换,多项式模型产生的转换坐标具有相对较好符合性。
3)当两个不同坐标系高精度成果相互转换,Bursa模型产生转换坐标即保持高精度,又有高符合性。
[1] 陈俊勇.中国现代大地基准-中国大地坐标系统2000(CGCS 2000)及其框架[J].测绘学报,2008,37(3):269-271.
[2] 程鹏飞,成英燕,文汉江,等.2000国家大地坐标系实用宝典[M].北京:测绘出版社,2008.
[3] 杨元喜,徐天河.不同坐标系综合变换法[J].武汉大学学报:信息科学版,2001,26(6):509-513.
[4] 王解先.王军,陆彩萍.WGS-84与北京54坐标的转换问题[J].大地测量与地球动力学,2003,8(3):70-73.
[5] 王文利,程传录,陈俊英.常用坐标转换模型及其实用性研究 [J].测绘信息与工程,2010,35(5):37-39.
[6] 鲍建宽,李永利,李秀海.大地坐标转换模型及其应用[J].测绘工程,2013,22(3):56-60.
[7] 李东,毛之琳,廖文兵,等.CGCS2000向城市独立坐标系转换精度分析与估计研究[J].测绘通报,2013(10):8-10.

