附加误差修正的GM（1，1）模型在卫星钟差预报中应用

刘铁柱，杨登科，马向向

（1．郑州市市政工程勘测设计研究院，河南 郑州450046；2．华亭煤业集团公司，甘肃 平凉744000）

在卫星导航系统中，卫星钟差产品的实时性与精度是决定系统实时导航定位的关键因素，尤其是精密单点定位技术（PPP）［1－3］。目前，IGS提供的事后精密钟差产品有13 d的滞后时间，即便超快速精密钟差也有3 h的延迟，因此，使得PPP技术主要停留在事后处理模式中，然而PPP的真正优势在于实时应用，因此，针对卫星钟差预报，已有大量学者开展相关研究［4－7］，并得出许多有益的结论。目前，采用GM（1，1）模型预报卫星钟差已得到大多数学者认可［8－9］。为提高 GM（1，1）模型预报精度，又有学者对GM（1，1）模型进行改进研究［10］，但其改进方法较为复杂，不利于编程实现与实际应用。为此，本文通过大量统计实验，提出一种附加误差修正的GM（1，1）模型，并与传统 GM（1，1）模型进行比较。实验结果表明，方法明显改善卫星钟差的预报精度。

1 附加误差修正的GM（1，1）模型

1．1 GM（1，1）模型原理

GM（1，1）模型基本思路如下［11－12］：假定x（0）（k）为原始钟差数据序列，其中k＝1，2，…，n，即

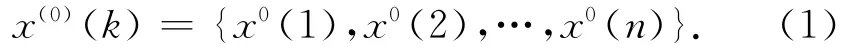
对序列x（0）（k）进行一次累加，生成一个新的累加序列，如式（2）所示。

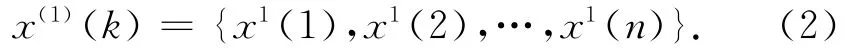
一般来说，可以认为累加序列x(1)k 是时间t的连续函数，将其用一阶微分方程来表示

式中：a为发展系数；u为内生控制灰数。通过最小二乘法求解式（3）的微分方程，算式为

式中：B为（n－1）×2阶矩阵，Y 为（n－1）×1阶矩阵。

由最小二乘求解得模型的时间响应函数为

将时间代入式（7），并对其进行一次累减，即可得到原始数据模型

其中：当k≤n时，得到的值是原始数据的拟合值；当k＞n时，得到的数据为预报值。

1．2 误差修正思路

GM（1，1）模型预报卫星钟差的残差在短时间内一般为系统性的偏差，尤其当卫星钟差呈现单调递增与递减时，为此，本文提出利用GM（1，1）模型预报残差进行二次预报，其基本思路如下：假定要预报未来200个数据，首先，利用GM（1，1）模型预报300个数据，其中前100个预报数据的观测值已知；其次，利用前100个数据的预报残差求解得到一个线性模型；最后，利用该模型对剩下的200个预报数据进行补偿，从而削弱其系统偏差，提高GM（1，1）模型预报的精度。同时，为了提高其预报的可靠性与稳定性，应对前100个预报数据进行统计，若85%的预报残差的绝对值小于1 ns且最大值小于1．5 ns，则进行误差修正，若未能满足上述条件，则认为该GM（1，1）模型的预报结果精度较高，因而不进行补偿，从而避免因错误补偿而造成更大的误差。

2 实例分析

为了验证本文方法的有效性与可靠性，采用IGS网站提供的5 min采样间隔的事后精密GPS卫星钟差数据进行实验分析。本文选用GPS系统第1 791周第一天的数据进行建模，预报接下来一天的钟差。值得注意的是：根据本文误差修正的思路，附加误差修正的GM（1，1）模型采用第一天的第177～188个数据进行建模，预报剩下的钟差以及第二天的钟差，根据上文提出的修正方法对预报结果进行补偿，而传统GM（1，1）模型是采用第一天最后12个数据建模，预报接下来一天的卫星钟差。由于卫星钟差的预报结果与卫星钟的类型有较大关系，因此，选用不同类型的卫星进行分析，卫星原子钟类型和卫星号对照表如表1所示，每个类型的原子钟各选用2颗，分别为 PRN01、PRN27、PRN05、PRN32、PRN11、PRN18、PRN07、PRN12。

表1 GPS卫星原子钟类型和卫星号对照表

图1为卫星PRN01与PRN07的预报结果，其中图（a）与图（b）分别是PRN01与PRN07卫星的钟差预报残差结果。为了更加清晰地看出其前100个钟差的预报残差，对其进行局部放大，其结果分别是各个子图中的小图。从局部放大图中可以明显看出，PRN01与PRN07卫星前100个预报结果小于给定的阈值，因此不进行补偿，此外，这两颗卫星采用GM（1，1）模型预报钟差的精度都在ns级，而影响导航定位精度的是预报钟差较大的卫星钟，因此，提高GM（1，1）模型较大偏差的钟差是提高导航定位精度的关键。

图1 未进行误差修正的卫星钟差预报残差结果

图2是PRN32与PRN11卫星的钟差预报结果，限于篇幅，其他卫星的预报结果本文并未给出，但其预报结果与图2基本一致。从图2可以看出，经过误差修正后的卫星钟差残差小于传统GM（1，1）模型的预报结果，尤其是PRN32卫星，经误差修正后的预报精度基本在ns级，相对于传统GM（1，1）模型的预报结果提高一个数量级。这说明本文提出的附加误差修正的GM（1，1）模型预报卫星钟差是有效的。为了进一步对比其预报效果，又分别统计这8颗卫星的预报残差的绝对值、最大值、最小值以及标准差，其结果如表2所示。从表2中可以看出，本文提出的附加误差修正的GM（1，1）模型预报精度都优于传统的GM（1，1）模型，尤其是标准差，附加误差修正的GM（1，1）模型预报精度有较大提高。此外，由于PRN01与PRN07卫星并未经误差修正，但其预报精度仍高于传统GM（1，1）模型，这说明GM（1，1）模型受模型初始值影响较大。

图2 进行误差修正的卫星钟差预报残差结果

表2 所有卫星钟差预报误差统计结果 ns

3 结 论

本文提出的附加误差修正的GM（1，1）模型相对于传统GM（1，1）模型在卫星钟差预报中，通过采用不同类型的卫星进行比较分析，结果表明，本文提出的修正模型能有效提高其预测精度，相对于传统GM（1，1）模型，标准差最大改善精度可达90%，最小也提高30%，同时，也保证其预测结果的稳定性，具有一定实际应用价值。另外，本文还为卫星钟差长期预报提出思路，即以天为单位，进行建模预报，并根据本文方法进行误差修正，最后对修正后的预报钟差进行内插，以满足其采样要求。尽管本文提出的模型精度有较大改善，但仍存在不足：1）GM（1，1）模型预报结果受建模数据的影响；2）在表2中PRN01与PRN07卫星本文并未进行改进，而是直接采用GM（1，1）模型的预报结果，尽管其预报精度仍是ns级，已满足导航精度要求，但如何在其基础上提高精度，仍是下一步的研究目标。

［1］ 于合理，郝金明，刘伟平，等．卫星钟差超短期预报模型分析［J］．大地测量与地球动力学，2014，34（1）：161－164．

［2］ 韩保民，欧吉坤．基于GPS非差观测值进行精密单点定位研究［J］．武汉大学学报：信息科学版，2003，28（4）：409－413．

［3］ WANG Jigang．Prediction of clock errors of ato mic clocks based on modified linear combination model［J］．Chinese Astrono my and Astrophysics，2011，35：318－326．

［4］ 王宇谱，吕志平，陈正生，等．一种新的导航卫星钟差预报与内插方法［J］．大地测量与地球动力学，2013，33（4）：112－116．

［5］ 王颖，徐波，杨旭海．一种利用泛函网络进行导航卫星钟差预报的方法研究［J］．宇航学报，2012，33（10）：1401－1406．

［6］ 黄观文，杨元喜，张勤．开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报［J］．测绘学报，2011，40（1）：15－21．

［7］ 郑作亚，党亚民，卢秀山，等．附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究［J］．天文学报，2010，51（1）：95－102．

［8］ 李玮，程鹏飞，秘金钟．灰色系统模型在卫星钟差短期预报中的应用［J］．测绘通报，2009（6）：32－35．

［9］ 崔先强，焦文海．灰色系统模型在卫星钟差预报中的应用［J］．武汉大学学报：信息科学版，2005，30（3）：447－449．

［10］陆晓峰，杨志强，贾小林，等．灰色系统理论的优化方法及其在卫星钟差预报中的应用［J］．武汉大学学报：信息科学版，2008，33（5）：492－495．

［11］孙泽信，庞逸群，黄腾．改进的灰色模型在建筑物沉降预测中的应用［J］．测绘工程，2010，19（3）：59－62．

［12］唐争气，谭志强．灰色时序组合模型在基坑监测中的运用［J］．测绘工程，2014，23（2）：49－53．