基于空间约束外点处理的图像非盲去卷积

陈幼芬，廖斌

（1.顺德职业技术学院电子与信息工程学院，广东 佛山 528333；2.湖北大学计算机与信息工程学院，湖北 武汉 430062）

0 引言

模糊图像的逆处理过程称为图像去卷积，其目的是由模糊图像恢复出清晰图像，以达到图像在视觉上的改善［1］.给定一幅输入的模糊图像y，现有的去模糊方法中为模糊图像建立的线性模糊模型可以表示为：y=k*x+n.其中，k是模糊核，x是潜在的清晰图像，n是噪声，*是卷积算子.图像盲去卷积方法就是通过输入的单幅模糊图像y来求解出两个未知量k和x，这显然是一个病态问题.图像非盲去卷积方法为了避免这个问题先估计出一个模糊核k，结合给定的模糊图像y，来估算出潜在的清晰图像x［2-4］.

人们已经提出很多非盲去卷积方法，包括经典的维纳波滤器、基于图像先验知识的优化方法等［5-7］.但是，即使模糊核已很好的估计出来，这些方法也很可能会得到一些含有严重振铃效应的结果.究其原因，主要是模糊图像的线性模糊模型没有考虑实际的图像采集、处理过程中经常出现的非线性像素点，即外点（相应地，称可以由线性模糊模型建模的像素点为内点）.文献［8］中分析了这些不同类型外点的产生的原因，并且分别进行处理，取得较好的去卷积结果.但是，该方法在基于外点处理估计潜在的清晰图像时，引入了清晰图像的稀疏先验知识.该先验知识是基于高斯核函数定义，其对于噪声和亮度变化有很强的敏感性.因此，该方法的表现并不鲁棒，在很多情况无法取得满意的结果.文献［9］和文献［10］假设图像中的噪声是一类噪声或者特定的噪声，不能有效地处理含有其它类型外点的情况，得到的结果存在严重的振铃效应.对于有噪图像，谭乐婷等［11］介绍了消噪-分离-消噪策略，可获得较清晰图像.

本文中提出一种基于空间约束外点处理的图像非盲去卷积方法.首先，借助于马尔科夫随机场［12］，构造图像邻域点的空间约束信息.然后，对模糊图像的内点和外点分别建模，基于空间约束信息，提出一种新的估计潜在清晰图像的目标函数.基于该目标函数，通过最大后验概率估计来求解潜在的清晰图像.在求解过程中，该方法可以直接且有效地利用EM（expectation-maximization）迭代算法［13］来优化参数.

1 本文中方法

1.1 非盲去卷积目标函数的构造 首先，根据图像的像素强度把像素点划分为内点和外点.为了有效区分这两类点，引进一个二值映射m.当观察到的像素强度xi是一个内点时，mi=1；否则mi=0，其中，下标i表示像素点索引.基于二值映射m，给定含有外点的模糊图像y和模糊核k，就可估计出最佳的潜在清晰图像x.由于不知道m的值，笔者用EM算法来计算m的期望值，然后用其进行去卷积处理.

为了建立能够准确描述外点的非线性模糊模型，假设传感器得到的是无噪声的模糊图像.然后，将该图像的像素强度剪切到相机的动态范围内，并加上噪声和外点.由此，非线性模糊模型可以表示为：

其中，c是剪切函数.当u在动态范围内时，c(u)=u；否则c(u)返回动态范围的最大或最小强度.假设添加的噪声n是空间独立的，且只有内点的噪声符合高斯分布.外点的观察强度与k和x完全独立，其值可以是动态范围内的任意值.同时，外点符合均匀分布，不对其提供任何先验.基于以上前提，找到最佳的潜在清晰图像x可以形式化为一个基于最大后验估计的目标函数求解问题，表示为

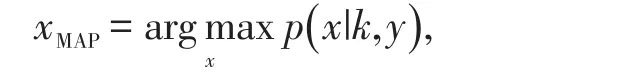
通过贝叶斯定理可以得到：

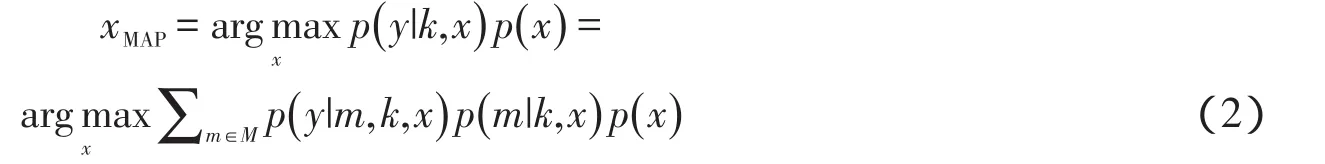
其中，M是m所有可能组合的集合.

基于马尔科夫随机场分布构造图像像素点的空间约束信息，并定义潜在清晰图像的先验为：

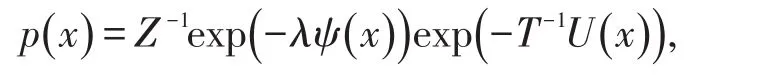
其中，Z是归一化常数，T是温度常数，U(x)是光滑先验.，其中，∇h、∇v分别表示沿着图像水平、竖直方向上的微分操作.，其中是控制光滑先验的温度值，∂i表示像素点x的邻域，Ni表示像素点x邻域的像素点个数，x0是x的初始估计值，j表示像素点索引.本文中，取Ni=25，β=12，Z=1，T=1，λ=1，α=0.6.

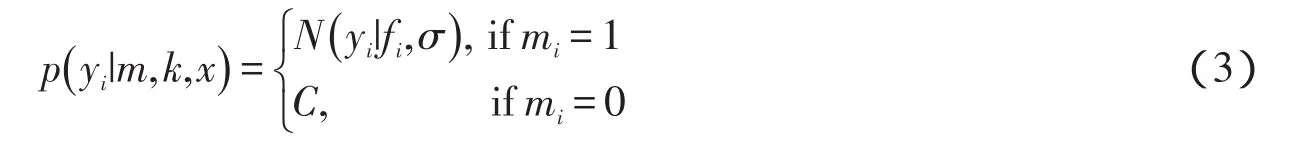
其中，f=k*x，N是高斯分布，σ是标准差.C是一个常量，定义为输入图像的动态范围值的倒数.

对于分类先验知识p(m |k,x)，假设m同样是空间独立的，即定义基于fi值的p(mi|fi)为：

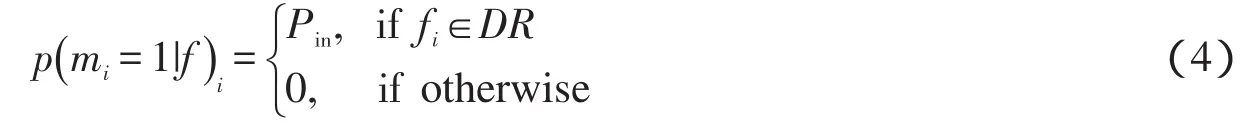
其中，DR∈[0 ,1]是动态范围，Pin∈[0 ,1]表示yi是内点的概率.在本文中，取Pin=0.92.

1.2 目标函数的优化求解 由于m有多种可能的组合，直接求解方程（2）很困难.本文中用EM算法来解决该问题.在E和M步骤中分别更新p(y |m,k,x) p(m |k,x)的期望和x的估计.在E步骤中，基于x的初始估计值x0，p(y |m,k,x) p(m |k,x)的期望Q(x ,x0)定义为：

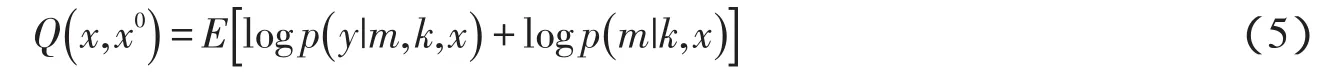
把式（3-4）式代入（5）式中，可以得到：

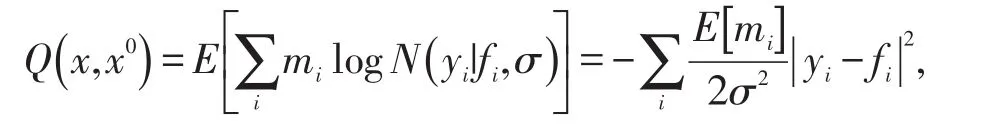
其中，E[mi]=p(mi=1|y,k,x0).并且，根据贝叶斯定理可以得到：

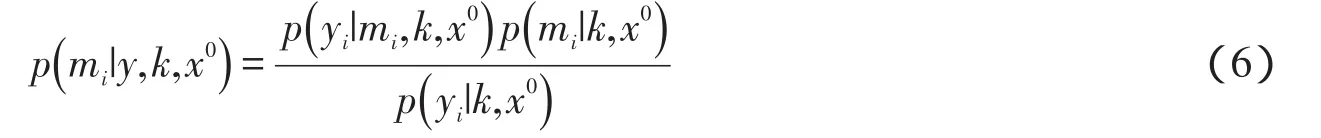
其中，p(yi|k,x0)=∑1mi=0p(yi|mi,k,x0)p(mi|k,x0).

将式（3-4）式代入（6）式可以得到：

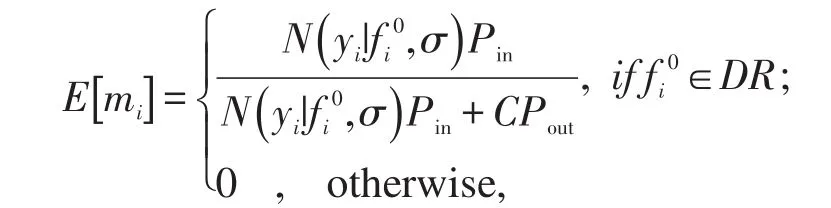
其中，fi0=k*x0，Pout=1-Pin.

在M步骤中，估计更新后的xn为：

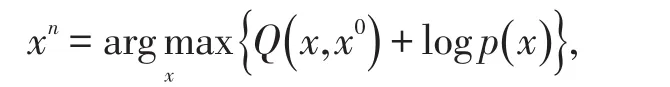
其等同于最小化式：

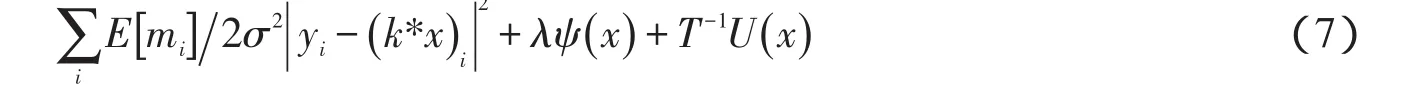
（7）式是一个关于x的二次方程，可以通过共轭梯度法来最小化求解.本文中取σ=0.5.

图1给出按照本方法对模糊图像进行非盲去卷积的一个示例.可以看出，本文中方法对含有非高斯噪声且进行剪切操作的模糊图像进行去卷积处理，可以得到很好的结果，没有产生振铃现象，有较好的抗噪能力.

图1 本文中方法去卷积的结果

2 实验结果与讨论

采用2.66 GHz四核CPU、NVIDIA GeForce GTX 760和8 GB内存的PC用Matlab编程实现提出的方法，并在合成或真实的图像上进行测试.如图2所示，用一个已知的模糊核将合成图像进行模糊处理后，添加一些不同类型、不同大小的外点.然后，分别使用文献［8］中的方法、文献［9］中的方法、本文中方法对这些合成图像进行去卷积处理.结果表明，本文中方法将底层纹理很好地恢复，并不是简单平滑处理外点，而是尽可能地恢复其原始像素强度.文献［8-9］中的方法对于小的外点，底层纹理恢复的较好.但是，对于大的外点，则不能精确地恢复，而是平滑掉.这是因为，本文中的模糊模型比文献［9］中的拉普拉斯分布、文献［8］中的像素点二分映射更好地描述了外点.

图2 富含纹理的模糊合成图像去卷积结果对比

如图3所示，对一幅均匀亮度的合成图像剪切高强度像素并加入均匀噪声.可以看到，文献［9］中的方法得到的结果出现了振铃效应.文献［8］中的方法得到的结果虽然有效抑制了振铃效应，但是得到图像效果并不清晰，说明其对于噪声还是比较敏感.本文中方法在均匀噪声以及饱和像素处都没有振铃效应，并且图像结果也非常清晰.

图3 均匀亮度的模糊合成图像去卷积结果对比

图4给出了对真实模糊图像的去卷积处理结果.利用文献［2］中的盲去卷积方法得到真实图像的模糊核.考虑到外点可能会影响估计的模糊核质量，从输入图像中把不存在明显外点（比如饱和像素）的区域剪切下来，并用其来估计模糊核.然后，用估计的模糊核对输入图像进行去卷积处理.结果表明，本文中方法对外点的处理最有效.利用文献［11］、文献［9］中方法结果存在着严重的振铃效应.利用文献［8］中方法结果虽然没有明显的振铃效应，但是结果不清晰，说明其中还含有高频噪声.

图4 真实模糊图像的去卷积结果对比

3 结束语

借助马尔科夫随机场分布，将图像邻域点的空间约束信息结合到估计潜在清晰图像的过程中.基于空间约束信息的外点分析，提出一个鲁棒的、基于EM算法的非盲去卷积算法.该方法可以有效地检测出外点，然后在去卷积时单独地处理这些点.将本文中的方法和以往的相关工作应用于合成图像和真实图像的去卷积处理并进行结果比较，实验结果表明，与当前主流的方法相比，本文中方法更有效，表现出更好的性能，基本上消除了以往方法中很常见的严重振铃效应，并且对于噪声和亮度变化有较强的抵抗能力.

［1］Chan T F，Shen J J.Image processing and analysis:variational，PDE，wavelet，and stochastic methods［M］.Philadelphia：Society for Industrial and Applied Mathematic，2005.

［2］Cho S，Lee S.Fast motion deblurring［C］//ACM Transactions on Graphics（TOG）.ACM，2009，28（5）:145.

［3］J Joshi N，Kang S B，Zitnick C L，et al.Image deblurring using inertial measurement sensors［J］.ACM Transactions on Graphics（TOG），2010，29（4）:30.

［4］Levin A，Weiss Y，Durand F，et al.Understanding and evaluating blind deconvolution algorithms［C］//Computer Vision and Pattern Recognition，2009.CVPR 2009.IEEE Conference on.IEEE，2009:1964-1971.

［5］Lucy L B.An iterative technique for the rectification of observed distributions［J］.The Astronomical Journal，1974，79:745.

［6］Richardson W H.Bayesian-based iterative method of image restoration［J］.JOSA，1972，62（1）:55-59.

［7］Banham M R，Katsaggelos A K.Digital image restoration［J］.Signal Processing Magazine，IEEE，1997，14（2）:24-41.

［8］Cho S，Wang J，Lee S.Handling outliers in non-blind image deconvolution［C］//Computer Vision（ICCV），2011 IEEE International Conference on.IEEE，2011:495-502.

［9］Bar L，Kiryati N，Sochen N.Image deblurring in the presence of impulsive noise［J］.International Journal of Computer Vision，2006，70（3）:279-298.

［10］Levin A，Fergus R，Durand F，et al.Image and depth from a conventional camera with a coded aperture［C］//ACM Transactions on Graphics（TOG）.ACM，2007，26（3）:70.

［11］谭乐婷，王娟.基于小波变换和ICA的新型有噪混合图像盲分离方法［J］.华中师范大学学报：自然科学版，2013，47（5）：632-635.

［11］赵宏宇，肖创柏，禹晶，等.马尔科夫随机场模型下的Retinex夜间彩色图像增强［J］.光学精密工程，2014，22（4）: 1048-1055.

［12］Bishop C M.Pattern recognition and machine learning［M］.New York:Springer，2006.