基于信息增量的弹道目标协同跟踪方法*
李志汇,刘昌云,于 洁
(空军工程大学 防空反导学院,陕西 西安710051)
0 引 言
在弹道导弹防御系统中,传感器在不同的时刻获得的量测主要由以下因素决定:1)传感器部署的位置;2)传感器的观测性能;3)当前目标的状态;4)战场环境。如何充分利用这些传感器获取的数据对弹道目标进行无缝交接和连续跟踪面临着许多挑战,迫切需要多传感器之间相互协同。协同跟踪属于传感器管理的范畴,其研究方法主要有协方差控制的方法及其改进方法[1,2]、基于信息论的方法[3~7]、后验克拉美罗界的方法[8]和基于多贝努力滤波的方法[9]等。
根据弹道导弹防御系统中对弹道目标跟踪的要求、以及弹道目标的特点,把信息增量的方法引入到多传感器弹道目标的协同跟踪问题中。采用无迹卡尔曼滤波(unscented Kalman filtering,UKF)计算不同时刻各传感器对弹道目标的信息增量,选择信息增量最大的传感器对弹道目标进行跟踪。仿真表明:所提的方法能够及时动态地选择能提供给目标最多信息的传感器对弹道目标进行跟踪,并能选择合理的传感器交接班时机。
1 多传感器协同跟踪问题描述
反导传感器网络对弹道目标协同跟踪的示意图如图1所示,多传感器弹对道目标的跟踪与对其他目标跟踪的不同之处在于:弹道目标轨迹跨度范围大,会不断脱离一个传感器的视野而进入另一个传感器的视野,需要多个传感器之间进行协同跟踪;弹道目标速度快,需要提前规划传感器部署方案。在局部战场态势下,从传感器资源优化的角度,当多个传感器可以同时对弹道目标进行跟踪时,选择其中一个对其进行跟踪,既能提高传感器网的整体跟踪性能和资源效能,也能提高传感器的生存时间和反侦察的能力。

图1 多传感器对弹道目标协同跟踪示意图Fig 1 Diagrams of multi-sensor collaboration tracking on ballistic target
2 自由段弹道目标跟踪模型与算法
根据文献[10]提出的分段匀加速模型,建立自由段弹道目标分段匀加速跟踪模型,如图2 所示。
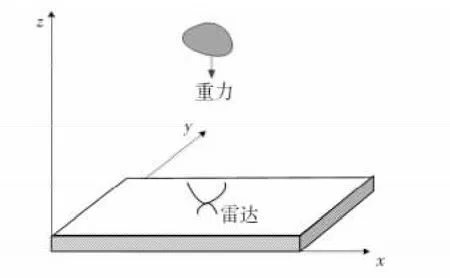
图2 自由段弹道目标运动模型假设示意图Fig 2 Kinematic model of ballistic target in free flight
在这种假设下,得到弹道目标的分段匀加速模型离散形式
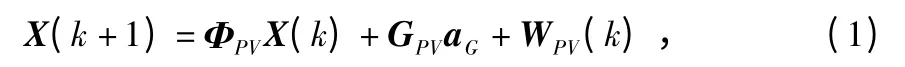
雷达的量测方程为
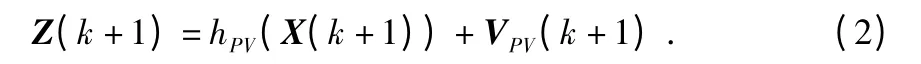
其中,Z(k+1)=[r(k+1),θ(k+1),φ(k+1)]',)为目标与雷达的距离,和φ(k+1)=分别为目标的方位角和俯仰角,VPV(k+1)为协方差矩阵为R(k+1)的高斯量测噪声。
采用不敏卡尔曼滤波进行跟踪,一方面是因为上述模型的雷达量测方程是非线性的,UKF 采用对概率密度函数的近似代替了扩展卡尔曼滤波(extended Kalman filtering,EKF)中对非线性函数的近似,具有更高的跟踪精度;另一方面,弹道目标的跟踪实时性要求很高,相对于粒子滤波(particle filtering,PF),UKF 的滤波速度更快。
3 信息熵与信息增量
Shannon 第一次提出采用信息熵作为信息的测量。在连续情形下,随机变量X 的信息熵为[4]
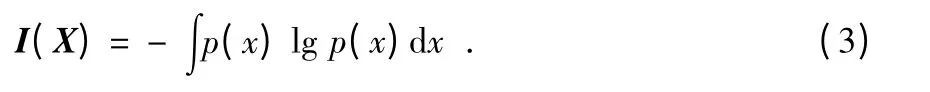
信息熵反映了随机变量X 的随机性,不能反映信息量的变化;信息熵的变化才能反映信息量变化的多少。针对跟踪问题,采用信息论中先验信息熵与后验信息熵之间的差定义为信息增量,假设I(X)表示先验信息熵,I(X|z)表示后验信息熵,则
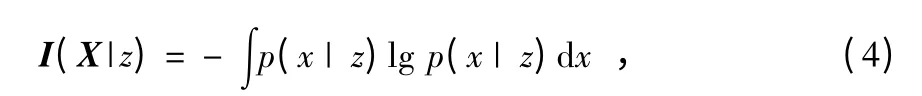
那么,由传感器的量测z 带来的信息增量为

在目标跟踪过程中[11],协方差阵P 表示目标状态的不确定性,因此,信息增量可以利用观测前后协方差矩阵的变化来计算。
针对随机变量X,假设其概率密度函数p(x)服从标准正态分布,根据香农信息论,其信息熵为
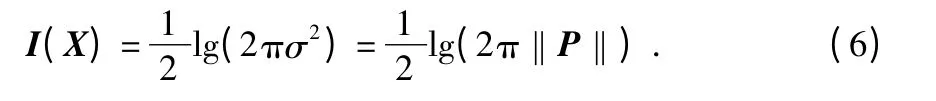
传感器对目标观测前,其预测协方差阵为P(k+1|k),先验信息熵为

传感器对目标观测后,其状态估计协方差阵为P(k+1|k+1),后验信息熵为

观测前后信息熵的差即信息增量为
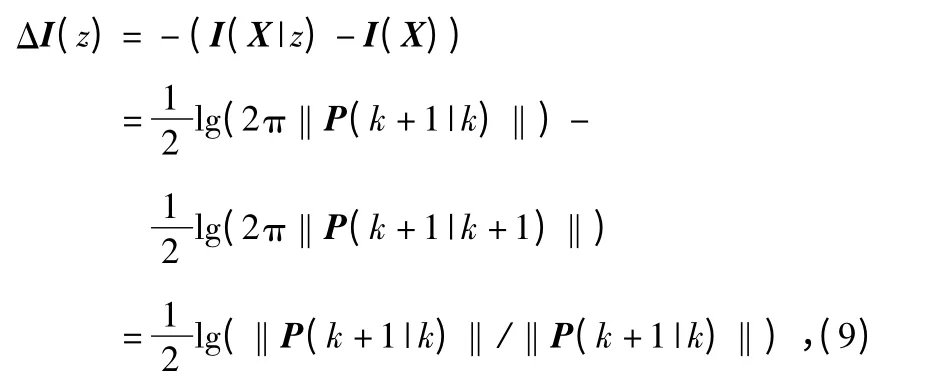
式中 ‖P‖为协方差阵的范数,对式(9)进行化简[6],得到
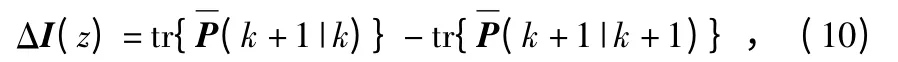
4 协同跟踪算法实现步骤
假设条件:k 表示时间,N 为传感器的只数,L 为协同跟踪时间,i 表示第i 只传感器。
初始化:k=0,i=1,初始化N 只传感器的滤波初值。
1)第i 只传感器采用UKF 跟踪目标,并利用式(10)计算第i 只传感器k 时刻的信息增量ΔIi,i=i+1,执行步骤(2)。
2)如果i <N,执行步骤(1);否则,执行步骤(3)。
3)比较ΔII~ΔIN的大小,选出其中的最大值ΔImax和最大值对应的传感器标号imax,第imax只传感器采用UKF 算法对目标进行跟踪,执行步骤(4)。
4)将第imax只传感器跟踪获得的有关目标的信息送到网络中心,并置i=1,k=k+1,如果k <L,执行步骤(1);否则,执行步骤(5)。
5)协同跟踪任务结束,输出最优传感器分配结果。
5 仿真分析
5.1 仿真场景一
如图3 所示,假设仿真环境为多只传感器对一个自由段飞行的弹道目标进行跟踪,传感器网络采用3 部雷达{s1,s2,s3}进行仿真分析,假设雷达部署位置与目标的运动轨迹位于X-Z 平面内。三部雷达性能参数相同,距离和角度量测噪声标准差分别为100 m 和0.02°,采样间隔为T=0.5 s,部署坐标分别为(0,0)km,(87.45,0)km 和(176,0)km。目标由雷达s1飞向雷达s3,其初始状态为x0=1 km,z0=72.24 km,v0=1.589 km/s,目标的初始速度方向与X 轴正向夹角为φ0=12.8°,仿真时间为235 s。
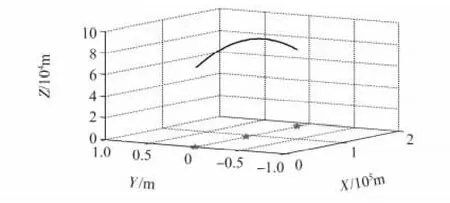
图3 目标的运动轨迹和雷达部署位置Fig 3 Motion trajectory of target and deployment location of radars
评价指标:采用目标估计位置(^x,^z)到实际位置(xr,zr)的距离误差均值作为跟踪性能的评估指标,即
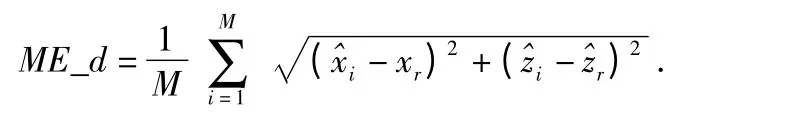
其中,M 表示Monto-Calo 次数。
通过单次仿真,得到雷达1 采用UKF 跟踪,三部雷达采用EKF 和信息增量法相结合的协同跟踪(EKF-ΔI)以及本文的方法(UKF-ΔI)的跟踪滤波距离误差均值对比,如图4所示。图5 为三部雷达采用UKF 获得的归一化信息增量对比。表1 为100 次蒙特卡罗实验的距离误差均值。
从图4、图5 和表1 可以看出:本文的弹道目标协同跟踪误差最小。首先,在非线性条件下,EKF 对非线性函数进行近似,造成了较大的线性化误差,固其滤波效果较差;其次,单部雷达虽然也用UKF 跟踪,但57 s 后,其归一化信息增量不是最大的,不能提供更多有关目标的信息,故本文方法选择信息增量最大的传感器对目标进行跟踪,提供了更多的信息,跟踪效果最好。

图4 距离误差均值对比Fig 4 Contract of distance error mean value

图5 归一化信息增量对比Fig 5 Contract of normalized information gain

表1 目标跟踪性能对比Tab 1 Contract of target tracking performance
图6 为本文方法得到的雷达跟踪选择结果。在三部雷达性能参数相同时,对雷达的选择近似于从雷达到目标的距离选择雷达。

图6 雷达跟踪选择结果Fig 6 Results of selection of radar tracking
5.2 仿真场景二
同仿真场景一中的布置情况相同,不同之处是三部雷达的距离和角度量测噪声标准差分别为400 m,0.05°;200 m,0.02°;50 m,0.01°,其他参数设置同仿真场景一。
采用本文的方法进行跟踪,对比方法为根据雷达离目标的远近选择雷达进行跟踪,简称UKF 距离法。图7 为单次仿真实验距离误差均值对比,图8 为两种方法得到的雷达选择结果,表2 为100 次蒙特卡罗实验距离误差均值。

表2 目标跟踪性能对比Tab 2 Contract of target tracking performance

图7 距离误差均值对比Fig 7 Contract of distance error mean value
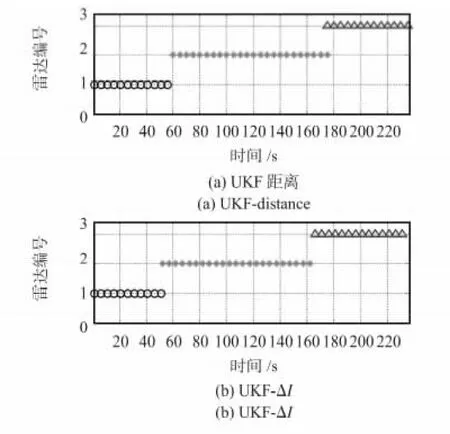
图8 雷达跟踪选择结果Fig 8 Results of selection of radar tracking
从图7、图8 和表2 可以看出:本文的方法比UKF 距离方法的整体跟踪误差较小。首先,在52 s 和176 s 左右,UKF 距离方法的距离误差均值相比本文方法略有增大的趋势;其次,跟UKF 距离方法对比,本文方法均提前进行雷达1 和雷达2 以及雷达2 和雷达3 的切换。表明在雷达性能参数不同时,本文方法能够及时动态地选择性能参数更好的雷达对目标进行跟踪,合理地选择雷达交接班的时机,从而提高整体的跟踪精度。
6 结 论
针对弹道导弹防御系统中的多传感器对弹道目标的协同跟踪问题。本文采用信息增量作为传感器跟踪性能的量测标准,并选择信息增量最大的传感器对弹道目标进行跟踪。通过仿真结果表明:本文方法能够及时动态地选择跟踪性能最佳的传感器对弹道目标进行跟踪,提高整体的跟踪性能,同时能够合理地选择传感器交接班的时机。
[1] Kalandros M,Pao L Y.Covariance control for multisensor systems[J].IEEE Transactions on Aerospace and Electrionic Systems,2002,38(4):1138-1157.
[2] 王 琳,于 雷,寇英信,等.以任务需求为驱动的多传感器资源管理方法[J].系统工程与电子技术,2010,32(9):1925-1930.
[3] 罗开平,姜 维,李一军.传感器管理述评[J].电子学报,2010,38(8):1900-1907.
[4] Aughenbaugh J M,La Cour B R.Sensor management for particle filter tracking[J].IEEE Transactions on Aerospace and Electrionic Systems,2011,47(1):503-523.
[5] 刘 钦,刘 铮.一种基于Rényi 信息增量的机动目标协同跟踪算法[J].控制与决策,2012,27(9):1438-1440.
[6] 李彬彬,冯新喜,王朝英,等.基于信息增量的被动多传感器资源分配算法[J].系统工程与电子技术,2012,34(3):502-507.
[7] 王 勇.基于Fisher 信息距离的被动传感器目标协同跟踪方法[J].传感器与微系统,2014,33(7):119-122.
[8] Kirubajan R tharmarasa.Decentralized sensor selection for largescale multisensor-multitarget tracking[J].IEEE Transactions on Aerospace and Electrionic Systems,2011,47(2):1307-1324.
[9] Hung Gia Hoang,Ba Tuong Vo.Sensor management for multitarget tracking via multi-Bernoulli filtering[J].Automatica,2014,50(2):1135-1142.
[10]Li X Rong,Jilkov Vesselin P.Survey of maneuvering target tracking—Part II:Motion models of ballistic and space targets[J].IEEE Transactions on Aerospace and Electrionic Systems,2010,46(1):96-119.
[11]张华睿.面向目标跟踪的传感器管理算法研究[D].长沙:国防科技大学,2006.

