弹丸姿态对感应式线圈靶测速精度影响
谢 彤,狄长安,王耀辉
(1.南京理工大学 机械工程学院,江苏 南京210094;2.南京理工大学 理学院,江苏 南京210094)
0 引 言
弹丸测速技术在武器系统的研制、定型、制表以及弹道学理论的研究中有着重要的地位,它是“诊断”武器威力、射程和射击精度的重要参数。目前,国内外常用的弹丸测速传感器有线圈靶、天幕靶、声靶和光幕靶等。与其他测速装置相比,线圈靶简便可靠,不与测试弹丸接触,不影响弹丸的运动轨迹[1],且不受气候和光线强弱等条件的限制。尤其在曳光弹和水下高速航行体测速中,感应式线圈靶发挥着重要的作用。但是在实际使用中,线圈靶测速精度会受到弹丸运动姿态和靶面安装位置的影响,如,在水下弹道的布靶时,弹丸速度较慢、散布较大,很难保证从各靶中心垂直穿过[2];在线圈靶安装时,两线圈靶中心位置不一致而造成弹丸以一定的偏移量穿越线圈靶等。因此,对线圈靶测速精度影响因素的研究有较高的实用价值。
目前,对于线圈靶测速误差分析主要考虑弹丸沿线圈靶轴线方向以一定的偏移量穿越线圈靶对线圈靶感应电动势的影响[3~5],而未考虑弹丸入射姿态对测速结果的影响。本文根据线圈靶测速原理和斯托克斯定理,建立了与弹丸姿态相关的线圈感应电动势特性的理论模型,利用Matlab软件对高速运动中的弹丸在入射时的感应电动势随偏航角、俯仰角和偏移量的变化进行了数值计算分析,进而获得弹丸姿态对感应式线圈靶测速精度的影响。
1 线圈靶测速原理
目前,测时仪常采用弹丸过靶时刻的特征点(过零点)触发,因此,线圈靶感应电动势的零点位置、过零点斜率和峰值大小等可以很好地反映出弹丸运动姿态对测速精度的影响。
2 感应式线圈靶感应电动势模型
根据弹丸测速的技术要求,线圈的径向尺寸一般为被测弹丸直径的20 ~40 倍。为了便于分析,可以忽略被测弹丸的尺寸,将其视为一个由正、负“磁荷”构成的磁偶极子[8],用磁矩p 表示它的磁学特性。因此,感应式线圈靶的物理模型可归纳为:磁矩为p 的点磁偶极子以速度v 穿越半径为a、匝数为N 的线圈靶。
为了便于分析线圈产生的感应电动势,建立如图1 所示的地面柱坐标系oxyz 和第一弹轴坐标系o'x'y'z'。点磁偶极子p 位于o'点,极矩沿x'轴方向以速度v 沿x 轴方向穿越感应线圈,入射点位于z 轴且距原点距离为b,磁偶极子的俯仰角和偏航角分别为θ 和ω。

图1 线圈靶测速模型Fig 1 Velocity measurement model for coil target
假设所讨论的空间里不存在传导电流,根据电磁场理论,在地面坐标系oxyz 中磁偶极子在空间任意一点Q 的磁矢势为

式中 μ0为空气的磁导率,其中
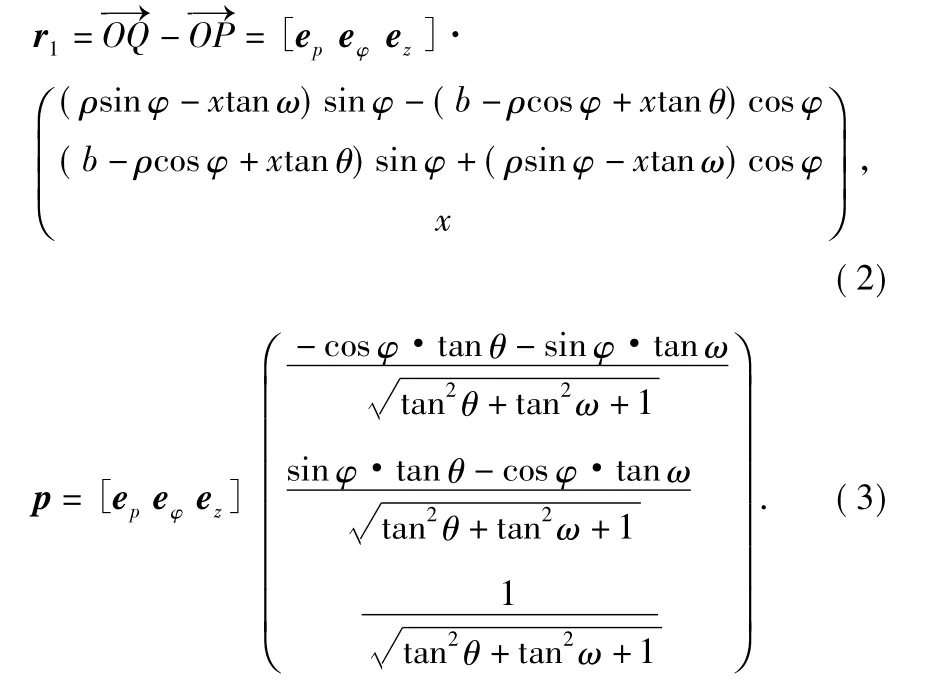
点磁偶极子p 产生的磁感应强度为

由斯托克斯定理可知,点磁偶极子p 穿越感应线圈的磁通量
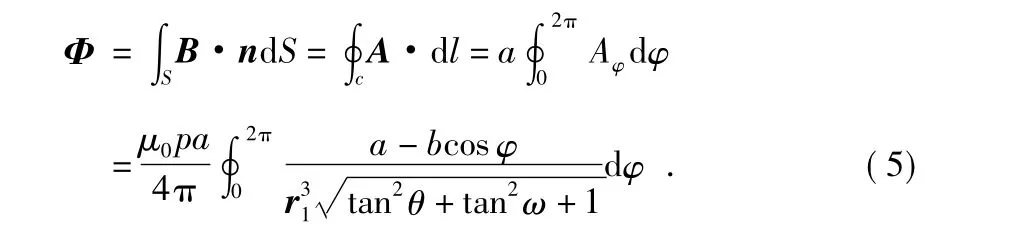
其中
相较于图文,短视频更加一目了然,消费者更加容易看见正真的商品,短视频更是以极富创意和观赏性的短视频内容来打动用户,从而引发用户发自内心的一种认同,继而心甘情愿地买单,名人效应流量非常的可观。

当弹头接近和远离线圈时,穿过线圈的磁通量发生变化,由电磁感应原理可知
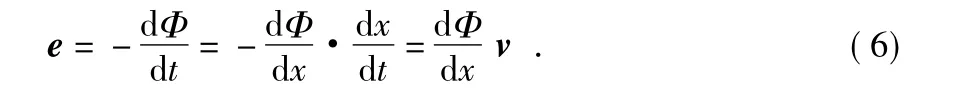
线圈靶的感应电动势为

式中 x 为弹丸到线圈靶的距离。因此,式(7) 揭示了线圈靶的区截信号和弹丸到线圈靶靶面距离间的关系。
3 线圈靶感应电动势特性分析
由感应电动势模型式(7)可以看出,系统感应电动势的误差与弹丸入射靶面的俯仰角、偏航角和偏移量有密切关系。由于式(7)没有解析解,只能利用仿真软件求解其近似值。本文以300 mm 口径线圈靶为例,利用Matlab 软件仿真分析了不同运动姿态下线圈靶的感应电动势特性,通过对其特征值的判断,分析弹丸运动姿态和偏移量对系统测速精度的影响。
3.1 偏移量对感应电动势的影响
当子弹沿轴线以偏移量b 穿过线圈靶时,线圈俯仰角和偏航角为零,线圈靶的感应电动势为

图2 为磁化弹丸沿线圈靶轴线方向分别以偏移量0,0.05,0.1 m 穿越线圈靶的感应电动势曲线。仿真曲线表明:高速运动的弹丸穿越感应线圈时,随着穿越位置距感应线圈轴线偏离量的增加,产生的感应电动势幅值逐渐增大;感应电动势峰值靠近靶面,峰值与谷值之间距离减小,零点附近斜率增大。弹丸以一定偏移量穿越线圈靶并不影响其产生感应电动势零点位置。因此,在测时仪用过零比较器提取特征值触发时,可以适当以一定偏移量垂直射击,提高信噪比,从而提高判读精度。
3.2 偏航角对感应电动势的影响

图2 偏移量对感应电动势的影响Fig 2 Impact of offset on EMF
根据式(7)利用Matlab 仿真偏移量为0.05 m、俯仰角为0 时,弹丸以偏航角0,π/6,π/3 的运动轨迹与感应电动势关系曲线。从图3 所示的仿真结果可知,当偏航角为π/3 时,感应电动势曲线变化趋势改变,同时出现多个零点。由于零点位置决定测时仪的触发时刻,多个零点的出现将给测时仪带来计时误差。因此,通过对式(7)零点的讨论可知,在偏移量一定条件下,当弹丸偏航角ω 绝对值大于ω0时,感应电动势曲线出现多个零点,ω0与偏移量b 关系如图4 所示。从图中可以看出:随着偏移量的增加ω0逐渐增大,由于偏移量具有不确定性,因此,弹丸偏航角大于0.685 rad时线圈靶感应电动势曲线出现多个零点。当ω 小于ω0时,弹丸穿越线圈靶靶面时刻的线圈靶感应电动势不为零,偏航角改变了感应电动势零点位置。随着偏航角的增加,感应电动势零点位置逐渐远离靶面,过零点斜率减小,感应电动势极值逐渐减小。
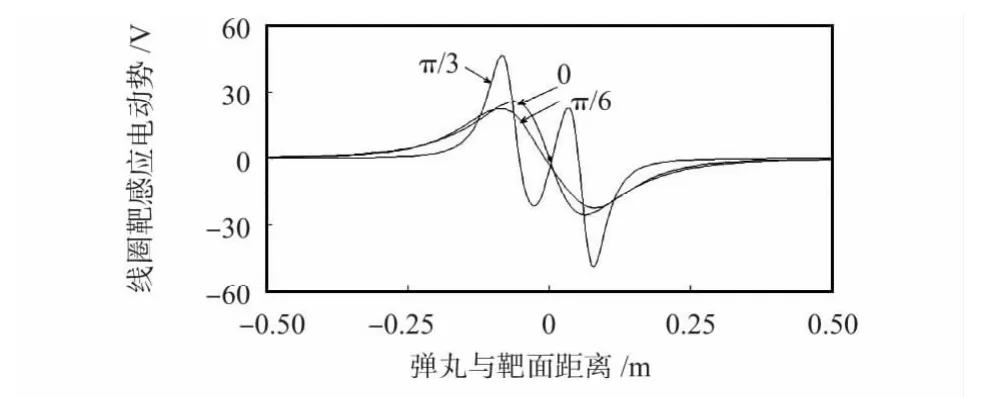
图3 偏航角对感应电动势的影响Fig 3 Impact of yaw angle on EMF

图4 感应电动势出现多个零点时偏航角与偏移量的关系Fig 3 Relationship between yaw angle and offset when EMF occur multi zero point
3.3 俯仰角对感应电动势的影响
如图5 所示仿真,b 为0.05 m,偏航角为0 时,弹丸以俯仰角0,π/6,π/3 的运动轨迹与感应电动势关系曲线。从图5 所示的仿真结果可知,线圈靶感应电动势与弹丸位置的关系呈现非对称分布。当俯仰角为π/3 时,感应电动势曲线出现多个零点。同3.2 节分析方法可知,当弹丸入射临界偏航角θ0为0.685 rad 时,感应电动势曲线出现多个零点,且随着偏移量的增加,临界偏航角逐渐增大。当θ <θ0时,弹丸穿越线圈靶靶面时刻的线圈靶感应电动势不为零,偏航角改变了感应电动势零点位置。随着偏航角的增加,感应电动势零点位置逐渐远离靶面,过零点斜率减小,感应电动势极值逐渐减小。

图5 俯仰角对感应电动势的影响Fig 5 Impact of pitching angle on EMF
在实际测速过程中,弹丸的俯仰角和偏航角同时存在,由于式(7)没有解析解,无法直接求得俯仰角和偏航角同时作用时感应电动势零点位置。因此,可以对俯仰角和偏航角分别赋值求取感应电动势为零时刻的弹丸位置。根据外弹道学理论可知,弹丸平稳飞行时的攻角(速度矢量与弹丸纵轴之间的夹角)一般在7°以内,图6 所示,曲面反映了偏移量为50 mm、ω 和θ 分别为-7°~7°入射对线圈靶感应电动势零点位置的联合影响。从图中可以看出:弹丸的偏航角对测速结果影响较大,而感应电动势零点位置受俯仰角影响较小。在俯仰角一定时,感应电动势零点关于偏航角呈线性变化,且随着偏航角角度的增加感应电动势零点位置逐渐远离靶面。当俯仰角为7°、偏航角从-7°变化到7°时,线圈靶感应电动势零点位置从-5.11 mm 变化到5.11 mm。此时,若线圈靶靶距为1 m,弹丸攻角所引入的测速误差为0%~0.511%;当偏航角为7°、俯仰角在-7°~7°变化时,线圈靶感应电动势零点位置在5.02 ~5.11 mm之间变化。此时,若线圈靶靶距为1 m,弹丸攻角所引入的测速误差为0.502%~0.511%。

图6 弹丸不同姿态下线圈靶感应电动势零点位置Fig 6 Zero point position of EMF of coil target at various attitude of projectile
4 线圈靶速度测试实验与验证
为了验证上述模型的正确性,设计了感应式线圈靶测速实验。实验系统由磁钢、感应式线圈靶、玻璃管、调理电路和数据采集系统组成。将一个高8 mm,直径为6 mm 径向充磁的圆柱形磁钢从1 m 高处沿直径7 mm 的玻璃管内以速度v 自由下落。速度v 由磁钢固定位置孔的装置控制,通过改变线圈靶的位置和角度模拟弹丸入射时的角度和偏移量,靶心始终保持在距磁钢50 mm 处。为使实验效果明显,磁钢以大角度入射,并且假设磁钢的磁感应强度保持不变且匀速下落。图7 给出了不同姿态和偏移量条件下,弹丸穿越线圈靶的感应电动势测试结果。从实验得到曲线可以看出:实际测量结果与软件仿真分析的感应电动势变化规律一致。图7(a),(b)中弹丸以偏移量0.05 m 和0.1 m 垂直入射靶面,感应电动势零点位置均出现在靶面零点处,随着偏移量的增加感应电动势峰值和过零点斜率逐渐增大。图7(c)~(f)中在偏移量一定的条件下,弹丸以偏航角和俯仰角分别为π/6 和π/3 入射靶面。当角度为π/3 时感应电动势曲线出现多个零点;当角度为π/6时,感应电动势零点逐渐远离零点位置。

图7 弹丸姿态对线圈靶感应电动势影响Fig 7 Impact of projectile attitude on EMF of coil target
5 结 论
1)当弹丸垂直入射靶面时,随着入射点与靶心的距离的增加线圈靶测速精度逐渐增大。
2)在偏移量相同下,弹丸的偏航角和俯仰角的大小会影响线圈靶的测速精度。在实际弹丸测速过程中,俯仰角的变化对感应电动势零点的影响较小,俯仰角所引起的测速误差可以忽略。而偏航角的变化对感应电动势零点的影响较大,在靶距为1 m 时误差为0%~0.5%。因此,在线圈靶测时仪用过零比较器提取特征值触发时,应将靶面安放在弹丸飞行的稳定阶段同时尽量增加靶距,以减小测速误差提高测速精度。
[1] 秦会国,马 峰,仲 霄,等.水中弹药的电磁感应测速方法研究[J].测试技术学报,2012,26(4):280-287.
[2] Di Changan,Kong Deren,Wang Changming,et al.Influence of projectile passing through single coil with a little deviation from axes of coil on measuring velocity[J].Journal of Ballistics,2008,20(3):100-103.
[3] 章启成,孔德仁,狄长安.感应式线圈靶感应电势模型及其分析[J].测试技术学报,2009,23(6):501-504.
[4] 郝光荣,张 越.弹丸穿越线圈靶偏移对测速精度的影响[J].四川兵工学报,2011(9):19-21.
[5] Li Boquan,Wang Xiaofei,Pan Haibin,et al.Study on error analysis of measuring projectile’s speed using induction-type coil target[C]∥2010 International Conference on Electrical and Control Engineering,2010:2084-2087.
[6] Xiong Xianfeng,Kong Deren,Ruan Xiaofeng.Mechanism analysis of induction-type coil target for velocity measurement[J].Advanced Materials Research,2011,30(3):666-670.
[7] 倪晋平,田 会,姜凌彦.测速线圈靶信号放大与转换电路[J].测试技术学报,2004,18(4):316-319.
[8] Di Chang’an,Shi Xiaoqin,Kong Deren.Study on offset measurement of underwater high-speed moving body based on single induction coil[J].Measurement,2014,47:422-426.

