矿柱下软弱夹层的极限承载力分析

殷 勇 乔来军 周国庆

(1.深部岩土力学与地下工程国家重点实验室，江苏 徐州221008;2.盐城工学院土木工程学院，江苏 盐城224051;3.中煤国际工程集团北京华宇工程有限公司，河南 平顶山467002)

地下采矿工程中为了保护矿井巷道、控制地表沉降、改善顶板控制条件等原因经常需要预留一些矿柱(包括非煤矿柱)，随着煤炭资源开采不断向深部发展，为确保安全，设置的矿柱尺度也越来越大，合理地进行矿柱设计并确保其稳定性对于煤炭资源的安全及高效开采具有重要的意义。

针对矿柱的稳定性研究，目前主要是从矿柱的强度出发分析其承载能力的大小。比如考虑到地下开采过程中应力重分布会引起矿柱上荷载的变化，从极限强度理论出发，以矿柱所承受的荷载是否超过矿柱的强度来判断其稳定性。围绕这方面的矿柱稳定性研究内容涉及矿柱上荷载的计算理论以及矿柱的强度理论，已有不少学者对此进行了深入研究并得到了一些工程实用计算理论，如矿柱载荷计算的压力拱理论［1］、有效面积理论［2］、A. H. Wilson 两区约束理论等［3］;矿柱强度理论也形成了瞬时强度理论体系和长期强度理论体系［4-5］，并考虑了影响矿柱强度的多种因素［2］。这些理论主要围绕将矿柱作为支撑结构分析各种荷载因素对其稳定性的影响，实际上，矿柱结构稳定性的影响因素很多，除了从矿柱自身强度及其作用荷载进行分析外，矿柱下伏地层条件与矿柱的稳定性也有很大关系。在这方面，矿柱下伏地层的承载能力是保证矿柱安全的重要因素。对于矿柱下伏常规均质地层的承载力分析可以参照上部结构地基承载力的一般算法，但是对于一些特殊的地质构造情况，如矿柱底板下存在一定厚度软弱夹层时其承载力的计算则并没有相对成熟的方法。此外，从地质构造条件上看，地层中的软弱夹层是一类广泛存在的地层结构，在采矿及地下洞室开挖中经常遇到，容易给采矿工程及地下工程建设带来安全隐患。

目前，煤矿工程及其他地下工程中对于软弱夹层的研究多数偏向于夹层的存在对井下巷道或边坡稳定性的影响［6-8］，对矿柱及其他地下结构下伏软弱夹层的承载特性研究较少，相应的承载力分析理论还比较缺乏。因此，实际工程中，对于矿柱下伏软弱夹层的地层极限承载力仍需要进一步研究其实用计算方法。

1 软弱夹层破坏模式

含软弱夹层的地层结构本质上属于层状地基，目前常用的一些层状地基承载力计算公式［9-10］，如汉森加权平均法、魏锡克法、迈耶霍夫法等，多数是基于均质地基承载力进行经验修正得到，其极限状态的破坏模式主要围绕整体剪切破坏、局部剪切破坏、冲剪破坏3 类。但含有软弱夹层的地层结构在极限状态时破坏模式已不同于均质地基或层状地基中的剪切破坏，由于软弱夹层厚度不大且强度较周边岩土层低，极限状态时更易出现侧向塑性挤出的破坏型式，类似于两块刚性平行板之间的挤压，其极限荷载也不能利用现有的承载力理论进行分析。我国《GB50290—98土工合成材料应用技术规范》、《SL225—98 水利水电工程土工合成材料应用技术规范》、《HG/T20708—2011 化工建(构)筑物地基加筋垫层技术规程》对加筋垫层下的软弱夹层也均指出这种塑性挤出破坏模式，要求按此破坏模式进行夹层的稳定性验算。张道宽［11］、Azam［12］、Christopher 等［13］的研究成果也表明软弱夹层的极限荷载受侧向塑性挤出破坏模式的影响。对于含有软弱夹层的矿柱地基而言，矿柱底板在矿柱荷载下容易发生冲切破坏，使得底板及下部岩土层形成类似于上下准刚性岩土层挤压中间软弱夹层的破坏模式(图1)。围绕该破坏模式，采用理想塑性材料挤压模型，将软弱夹层上下岩土层面当做刚性层面，考虑软弱夹层面不同的剪应力条件，通过上限法计算了软弱夹层的极限荷载，得到的极限荷载计算式可以为矿柱下含软弱夹层的地层承载稳定性分析提供参考，以便进行矿柱的优化设计。

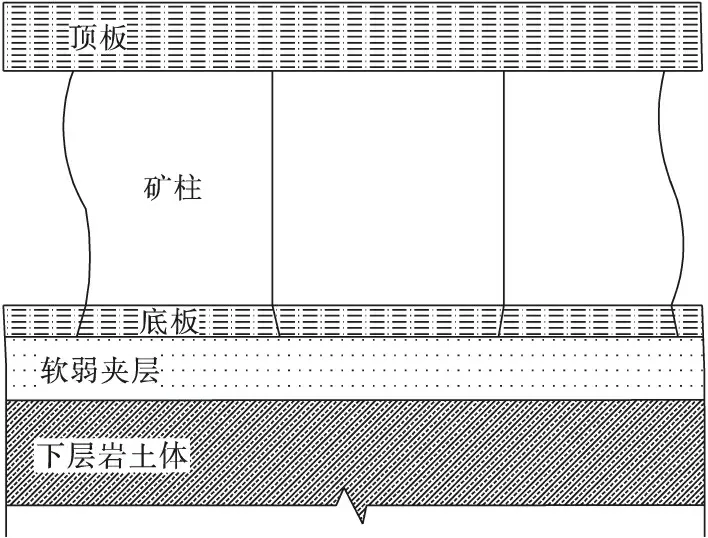
图1 矿柱下卧软弱夹层示意Fig.1 Illustration of soft interlayer underlying pillar

2 夹层结构的挤压模型

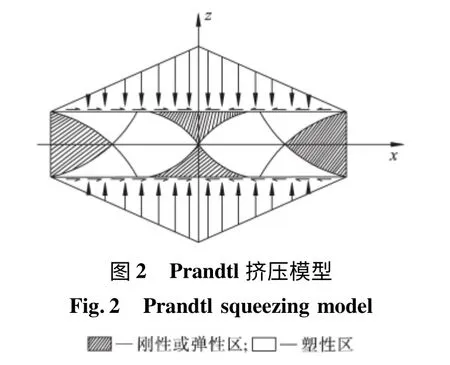
夹层挤压问题是一个经典的力学问题，Prandtl(1923)首次对该问题进行了研究，采用图2 所示的平面挤压模型，根据塑性理论滑移线方法提出了2 个粗糙刚性平面间塑性材料的挤压力解答。张国霞将Prandtl 的解答用于筏板基础下软弱夹层的承载力计算，提出了薄层挤压理论并被相关的行业规范引用于软弱夹层的稳定性分析［14］。虽然Prandtl 解答被众多学者引用于挤压力的分析，但该解答仅假设板面为完全粗糙，板面与材料间不发生任何滑动，而且解答还存在一些与实际应力边界条件不符的情况［15］，只能是一个较为近似的解答。

实际上，对于夹层材料的极限挤压力，一方面与材料的强度有关，另一方面还与夹层面的摩擦条件及夹层的宽高尺度有关。Hill［16］、Sherwood［17］考虑了不同的壁面摩擦条件，对刚性平板及圆盘挤压塑性材料的极限荷载进行的研究表明，采用不同的摩擦条件得到的极限压力有很大差异，但研究者仅假定板面服从单一滑动摩擦条件或具有一定粗糙度的情况。翁克索夫［18］通过大量实验验证和理论分析对刚性平板挤压塑性材料时的接触应力随摩擦条件的变化进行了系统研究，认为接触面的应力分布决定于板面摩擦条件和试样宽高比。对于夹层宽高比较大且板面摩擦系数0 ＜μ≤0.5 的情况，板面的摩擦条件分为黏滞区、制动区、滑动区，板面的剪应力分布如图3 所示，μ＞0.5 时末端的AB 段消失，板面属于完全粗糙状态，剪应力恒定并等于材料的剪切强度。

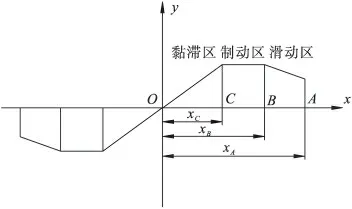
图3 板面摩擦条件分布Fig.3 Distribution of friction conditions on plate surface

下面基于翁克索夫得到的板面剪应力分布规律，利用Prandtl 塑性挤出破坏模式和极限分析上限法对塑性夹层结构的极限挤压力进行求解，提出矿柱下伏软弱夹层的极限荷载计算方法。考虑到目前房柱式采煤法中矿柱的布置形式通常有2 种，一种是连续条带式矿柱，另一种是不连续的断面为圆形的矿柱，因此针对这2 种情况分别根据平面应变条件及空间轴对称条件下的挤压模型进行分析。

3 极限挤压力解答

3.1 平面应变条件

采用图4 所示平面应变挤压模型，向内沿y 方向取单位厚度，设宽度为b 的刚性压板以速度v0压缩高度为h 的理想塑性材料，材料水平向挤出速度为vx。假设整个位移速度场是连续的，材料内部不存在速度间断面，根据体积不变及y 方向应变率εy= 0 的条件，可得

2vxh = 2xv0，

即

根据几何方程可得

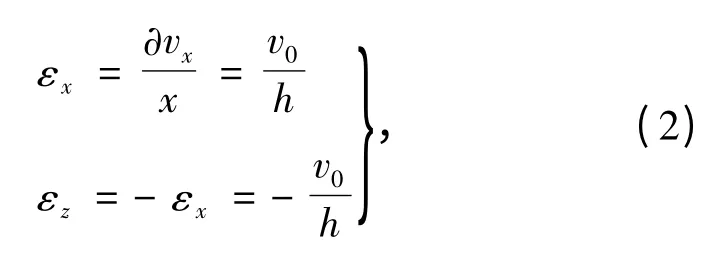
式中，εx、εz分别为x 和z 方向的应变率。

图4 挤压模型Fig.4 Squeezing model

考虑Mises 屈服准则，理想塑性变形功率可写为［23］

式中，σ0为材料单轴屈服应力，(k 为材料强度，对于软弱夹层可取其不排水饱和强度);表示等效塑性应变率，由下式确定:

根据式(2)、式(3)、式(4)可求得到塑性变形功率(由于对称，取一半模型计算):

下面计算板面接触摩擦引起的耗散功率，考虑到软弱夹层的厚度远小于其水平尺度，因此这里采用翁克索夫如图3 所示的板面摩擦规律［19］，其中3 个不同的板面摩擦条件如下。

黏滞区OC 段(0 ≤x ≤xC= h):

式中，σz表示库伦摩擦条件下板面竖向应力，

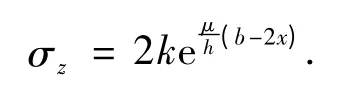
板面上接触摩擦引起的耗散功率可按下式计算:

将式(1)、式(6)、式(7)、式(8)代入式(9)可得

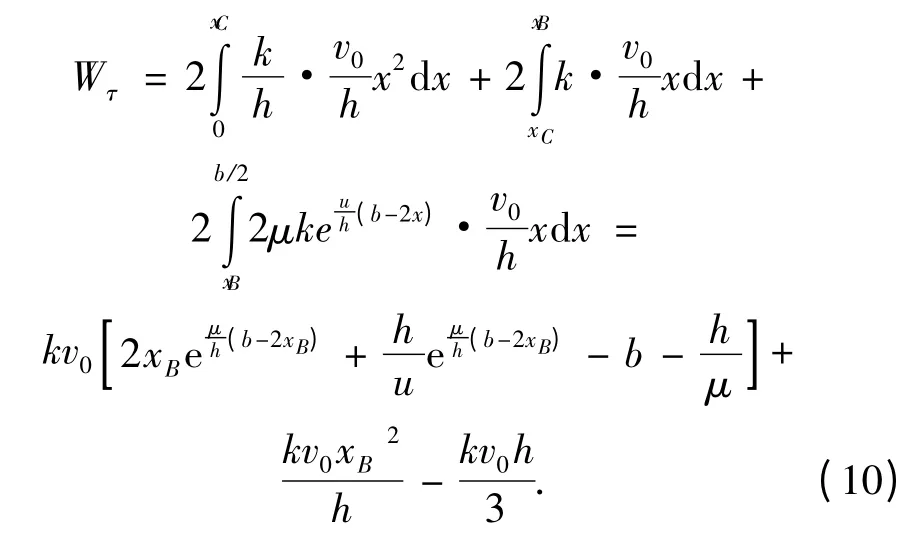
根据上限定理，材料的外部功率等于内部变形功率与界面摩擦耗散功率之和，整个板面的极限压力Q可按下式得到:

3.2 轴对称条件

轴对称条件下的挤压模型与图4 挤压模型类似，半径为R 的上部刚性压板以速度v0压缩高度为h 的理想塑性材料，假设材料处于均匀连续挤压变形过程，与z 轴垂直的断面在变形中仍保持为圆形截面，径向挤出速度为vr。根据体积不变条件，可得

πr2v0= 2πrhvr，

即

由几何方程可得各方向的应变率

根据式(3)计算轴对称条件下塑性变形功率为

板面接触摩擦引起的耗散功率计算方法与平面问题类似，仍采用翁克索夫板面摩擦条件。

黏滞区OC 段(0 ≤r ≤rC= h):

滑动区AB 段(rB≤r ≤R):

将式(15)、式(16)、式(17)代入式(9)可得板面上接触摩擦引起的耗散功率

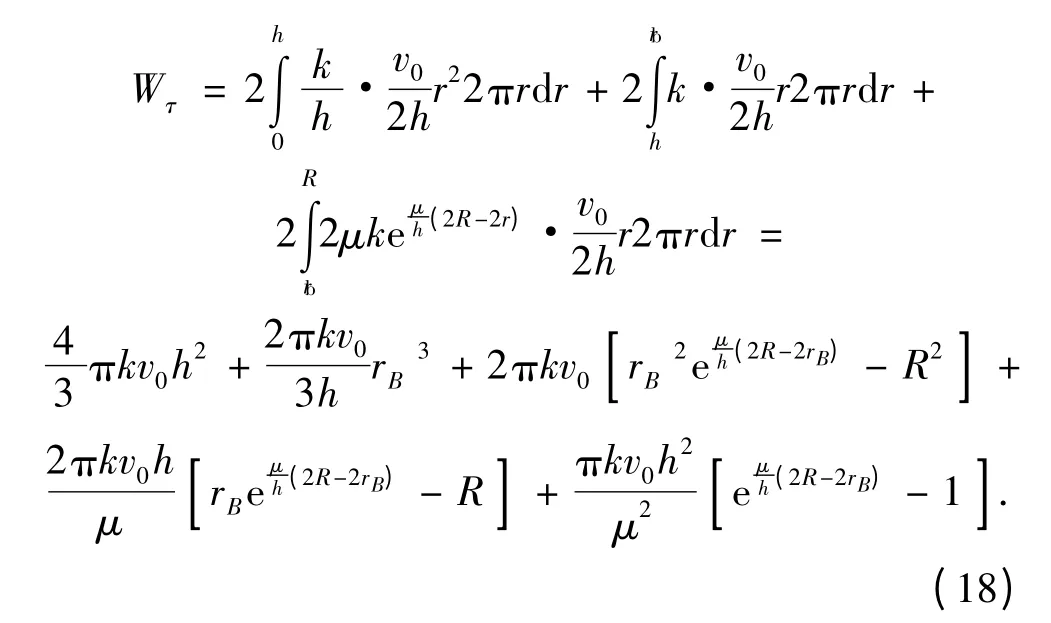
利用材料的外部功率等于内部变形功率与界面摩擦耗散功率之和，整个板面的极限压力Q 可按下式得到:

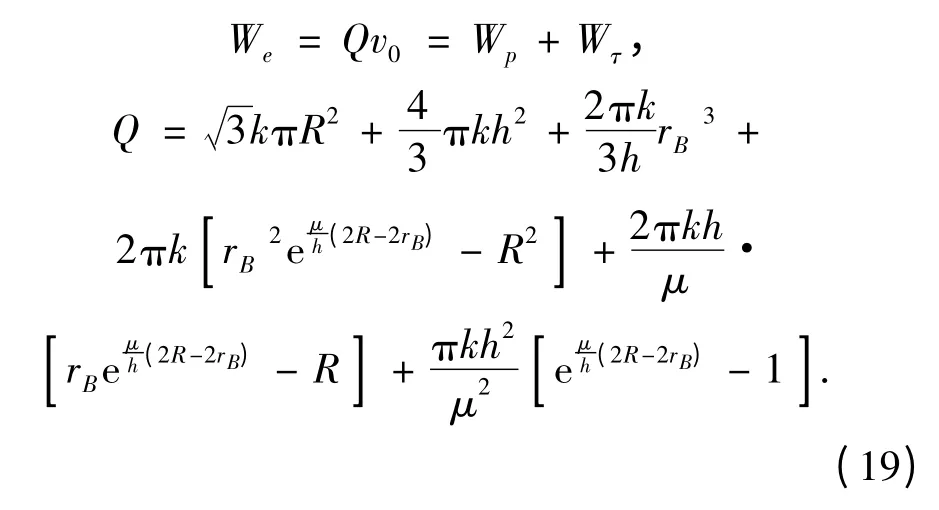
此外，根据前述极限压力计算过程可知，对于μ＞0.5 的情况，平面应变问题及轴对称问题中板面的摩擦条件将分别由式(6)、式(7)和式(15)、式(16)构成，表明不存在极限状态的滑动区，此时计算的极限板面极限压力与μ=0.5 时相同。

4 结果分析与讨论

上述平面应变条件下和空间轴对称应力条件下的极限压力计算式(11)和(19)可分别用于条带式矿柱及圆形矿柱下软弱夹层的极限承载力分析。为便于对比分析本研究提出的计算方法，以平面问题为例，不失一般性，取软弱夹层参数宽b =1 ～10 m，厚度h=1 m，μ=0.1 ～0.5，分别按本研究方法、Prandtl理论以及板面摩擦条件全部为τ = 0 、τ = mk(m 为粗糙度系数，m=0 表示完全光滑，m =1 表示完全粗糙)、τ = μσz计算的极限压力结果如图5 ～图7 所示，其中极限压力以Q/k 表示。

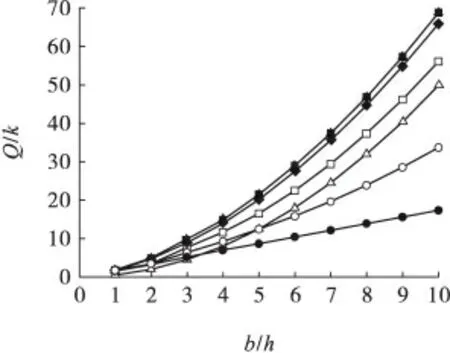
图5 本研究解答与Prandtl 解答的对比Fig.5 Comparison of solutions between this text and Prandtl

图6 本研究解答与摩擦条件τ=mk 的对比Fig.6 Comparison of solutions between this text and friction condition of τ=mk

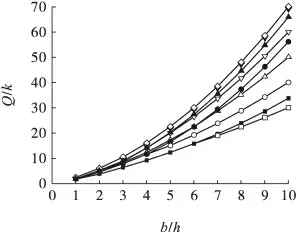
图7 本研究解答与摩擦条件τ=μσz 的对比Fig.7 Comparison of solutions between this text and friction condition of τ=μσz

由图5 计算结果可以看出，软弱夹层的宽高比及层面的摩擦系数对极限压力的影响具有一定的规律，软弱夹层的极限压力随夹层的宽高比增加而增大。在一定的宽高比下，极限压力随板面摩擦系数的提高而增大，但增加幅度逐渐减小，各种宽高比尺度下夹层的极限压力在摩擦系数接近0.5 时达到峰值。在较小的宽高比时板面摩擦条件对极限压力的影响不大，但随着夹层宽高比的增大，摩擦系数对极限压力的影响逐步增加，需要注意的是摩擦系数达到0.3 以上时其对极限压力的影响幅度趋于减小。

对比本研究方法计算结果与Prandtl 解答结果可以看出，Prandtl 解答按照夹层面完全粗糙的条件即(7)式考虑，计算的极限压力随宽高比增加而增大，在软弱夹层宽高比小于5 时计算值低于本研究方法μ=0.1 的取值，宽高比大于5 时介于本研究方法μ=0.1 及μ =0.2 之间，计算结果明显偏低。不考虑板面摩擦条件时(μ=0)极限压力总体上最小。

图6、图7 分别对比了本研究方法与板面采用单一剪应力条件τ = mk 及τ = μσz(图7 中以μ' 代表式中μ)的结果，总体上其他方法的计算结果低于本研究方法，在宽高比较小时与本研究方法的差值不大，随着宽高比增大，一般摩擦条件时其他方法计算的极限压力与本研究方法计算值差异较大，但在高摩擦系数或粗糙程度时与本研究方法基本趋于一致，其中m=1 时取值略低于本研究方法，μ' = 0.5 时取值略高于本研究方法。同时，宽高比一定的情况下，采用单一τ = mk 及τ = μσz条件计算的极限压力均随着摩擦系数或粗糙度系数线性增加，不能充分反映板面粗糙到一定程度时材料易在夹层面附近发生剪切破坏的情形。因此，对于宽高比较大的软弱夹层来讲，考虑非极端条件下的摩擦系数或粗糙程度时采用本研究方法计算能较好地反映实际夹层面的剪切条件。

根据上述不同软弱夹层宽高比及摩擦系数对极限压力影响规律的分析可知，对于矿柱下含有一定厚度的软弱夹层地基来讲，进行矿柱的设计时，增大矿柱截面宽度有助于提高下卧软弱夹层的极限承载力，在矿柱尺度有限制时，也可以采用局部注浆等方式改善软弱夹层面的摩擦条件进而有助于其承载力的发挥，但考虑增大夹层面摩擦条件的改善效果仅限于一定范围。

5 结 论

(1)基于翁克索夫得到的板面3 种剪应力分布规律，求解了平面应变条件及轴对称条件下软弱夹层的极限压力计算式，该计算式适用于夹层面摩擦系数0 ＜μ≤0.5 的软弱夹层，μ ＞0.5 时的软弱夹层极限压力与μ=0.5 时相同。

(2)对各种宽高比及板面摩擦系数的软弱夹层极限压力分析表明，软弱夹层的极限承载力随夹层结构宽高比的增加而增大，摩擦系数的增加也会提高夹层的极限承载力，在较大的宽高比时尤为显著，但摩擦系数增加到0.3 时其对极限压力的影响逐步减小，摩擦系数达到0.5 时其对软弱夹层的极限压力不再有影响。

(3)与软弱夹层面的其他剪应力假定条件相比，本研究采用的层面摩擦条件更符合塑性材料的挤压特性与实际，对于宽高比较大且摩擦系数取值非最大值的情况下本研究方法的解答总体上高于其他方法的计算结果。

(4)本研究得到的极限压力计算式可以从软弱夹层极限承载力的角度为下伏软弱夹层的矿柱地基设计及稳定性分析提供参考，同时对其他结构物下含软弱夹层的地层稳定性分析也具有一定的借鉴意义。

［1］ 吴立新，王金庄，郭增长.煤柱设计与监测基础［M］.徐州:中国矿业大学出版社，2000:25-26.

Wu Lixin，Wang Jinzhuang，Guo Zengzhang.Foundation for Coal Pillar Design and Monitoring［M］.Xuzhou:China University of Mining and Technology Press，2000:25-26.

［2］ 胡炳南. 条带开采中煤柱稳定性分析［J］. 煤炭学报，1995，20(2):205-210.

Hu Bingnan.Pillar stability analysis in strip mining［J］. Journal of China Coal Society，1995，20(2):205-210.

［3］ 谢和平，段法兵，周宏伟，等. 条带煤柱稳定性理论与分析方法研究进展［J］.中国矿业，1998，7(5):37-41.

Xie Heping，Duan Fabing，Zhou Hongwei，et al.Recent development of theory and analysis methods of strip pillar stability［J］. China Mining Magazine，1998，7(5):37-41.

［4］ 陈绍杰.深部条带煤柱长期稳定性基础实验研究［D］. 青岛:山东科技大学，2009:35-53.

Chen Shaojie. Basic Experimental Study on Long-term Stability of Deep Strip Coal Pillar［D］.Qingdao:Shandong University of Science and Technology，2009:35-53.

［5］ 邹友峰，柴华彬. 我国条带煤柱稳定性研究现状及存在问题［J］.采矿与安全工程学报，2006，23(2):141-145.

Zou Youfeng，Chai Huabin.Research status of strip coal pillar stability and its main problems in China［J］. Journal of Mining ＆ Safety Engineering，2006，23(2):141-145.

［6］ 伍国军，陈卫忠，杨建平，等. 基于软弱夹层损伤破坏模型的软岩巷道支护优化研究［J］. 岩石力学与工程学报，2011，30(S2):4129-4135.

Wu Guojun，Chen Weizhong，Yang Jianping，et al.Support optimization of soft rock roadways based on damage constitutive model for weak intercalated layers［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(S2):4129-4135.

［7］ 张 农，李桂臣，阚甲广.煤巷顶板软弱夹层层位对锚杆支护结构稳定性影响［J］.岩土力学，2011，32(9):2753-2758.

Zhang Nong，Li Guichen，Kan Jiaguang. Influence of soft interlayer location in coal roof on stability of roadway bolting structure［J］.Rock and Soil Mechanics，2011，32(9):2753-2758.

［8］ 丁立明，才庆祥，刘 雷，等. 软弱夹层对露天矿边坡稳定性的影响［J］.金属矿山，2012(4):41-58.

Ding Liming，Cai Qingxiang，Liu Lei，et al.Effect of weak interlayer on slope stability of open-pit mine［J］. Metal Mine，2012(4):41-58.

［9］ 钱家欢，殷宗泽.土工原理与计算［M］.北京:中国水利水电出版社，1996:371-386.

Qian Jiahuan，Yin Zongze. Geotechnical Principles and Calculation［M］.Beijing:China Water Conservancy and Electricity Press，1996:371-386.

［10］ Chugh Y P，Pula O，Pytel W M.Ultimate bearing capacity and settlement of coal pillar sub-strata［J］.International Journal of Mining and Geological Engineering，1990，8(2):111-130.

［11］ 张道宽.土工织物加强软土路基的研究［D］.北京:铁道部科研院，1987:116-120.

Zhang Daokuan. Embankment on Soft Clay Foundation Strengthened with Geotextile［D］.Beijing:China Academy of Railway Sciences，1987:116-120.

［12］ Azam G，Hsieh C W，Wang M C. Performance of strip footing on stratified soil deposit with void［J］. Journal of Geotechnical Engineering，1991，117(5):753-772.

［13］ Christopher B R，Holtz R D，Berg R R. Geosynthetic reinforced embankments on soft foundations［J］. Geotechnical Special Publication(GSP112)，2001:206-236.

［14］ 张国霞.基础工程学［M］. 北京:中国建筑工业出版社，1991:231-233.

Zhang Guoxia.Foundation Engineering［M］.Beijing:China Architecture ＆ Building Press，1991:231-233.

［15］ Hoffman O，Sachs G.Introduction to the Theory of Plasticity for Engineers［M］.Mcgraw-Hill Book Company，1953:154.

［16］ Hill R.The Mathematical Theory of Plasticity［M］. Oxford University Press，1950:246-256.

［17］ Sherwood J D，Durban D.Squeeze flow of a power-law viscoplastic solid［J］. Journal of Non-Newtonian Fluid Mechanics，1996，62(1):35-54.

［18］ 翁克索夫. 塑性的工程理论［M］. 秦开宗，译. 北京:科学出版社，1963:146-152.

Унксов ，Translate E П.Theory of Plasticity Engineering［M］.Qin Kaizong，Transtate.Beijing:Science Press，1963:146-152.