热电偶快速高精度测温算法*

闫 鑫，王晓娜，丁渊明，杨遂军，叶树亮

(1.中国计量学院 工业与商贸计量技术研究所，浙江 杭州310018;2.浙江省计量科学研究院，浙江 杭州310013)

0 引 言

随着热分析技术的快速发展，传统的热电偶测温技术已经不能满足其性能指标的要求，特别是在使用相对计算能力较差的单片机进行温度采集计算的应用中，很难在达到较高精度的同时拥有较快的响应速度。传统的电动势—温度转换方法［1，2］是根据热电偶的热电势值进行查表或者分段曲线拟合，求得当前温度值。查表法求取温度值虽然简单，但是需要存放大量的分度表数据，对系统的内存容量要求较高。分段曲线拟合法不需要大量的内存空间，但是分度表数据有限，随着分段拟合精度的提高，拟合公式所需要的数据也成倍增加，加之热电偶分度表数据的舍入误差，很难保证无限制提高拟合精度;相反，随着分段数目的增多，曲线拟合的精度可能会下降，即出现龙格现象［3］。由分度公式组成的方程求根法［4］虽然在计算精度上有了较大提高，但是由于公式的阶数较高，在计算时间上却远远不如分段拟合法。

针对上述问题，本文提出了一种新型测温算法，利用分段拟合法与查表法相结合求出温度值及其误差范围，即在方程求根法的思想上缩小二分法的查找区间，根据秦九昭简化算法降低分度公式运算复杂度，从而实现快速高精度的热电偶测温计算。

1 快速高精度算法原理

国际电工委员会ICE584—1 标准［5］提供的热电偶分度公式如式(1)所示

其中ai的值由分度表给出，其中T 型热电偶分度公式中温度t 阶数最高为14 阶。公式(1)给定的是热电偶的电动势关于温度的函数(E-T)，即给定某一温度值，由公式计算得到理想的热电动势值。实际使用中，通常是在测得热电动势的基础上计算出温度值，因此，需要把公式(1)变形如下

测得热电偶某一热电动势值E，使得求解公式(2)变为解一元多次方程的根。直接求解方程运算过程复杂不利于算法设计，而二分法利用无限逼近与叠代的数学思想，理论上能够快速无限接近实际值的根(即方程求根法思想)，因此，采用二分法求得方程的近似根。实际中，算法设计有2 个方面的难点:1)利用二分法求解需要给定一个初始区间，以免在不必要的区间段消耗时间;2)公式(2)存在很高的阶数，需要简化计算公式降低运算复杂度。因此，本文在方程求根思想上对算法作了改进如图1所示的改进，结合线性最小二乘法与查表法得到最接近实际温度一个温度值，利用导数确定二分法查找的初始区间，并且使用秦九昭算法简化高阶复杂运算公式，在保证精度的同时也提高了运算速率。

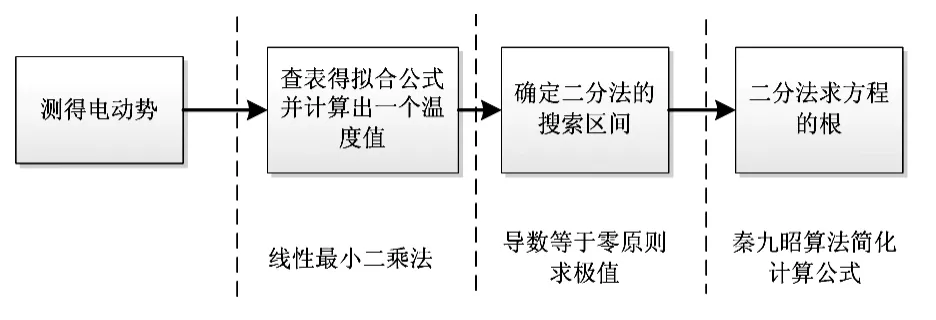
图1 算法整体思想Fig 1 Whole idea of algorithm

2 快速高精度算法设计

2.1 优化的方程求根方法

2.1.1 确定二分法温度区间

在测得热电偶的电动势E 后，用曲线拟合的方法得到电动势转换为温度的粗略关系式和该温度的误差范围，即确定了二分法的温度区间。

线性最小二乘法［2，6］是解决曲线拟合最常用的方法，基本思路是

其中，rk(x)为事先选定的一组线性无关的函数，ak为待定系数(k=1，2，…，m)。以N 型热电偶为例，由于其分度表公式的阶数比较高，在保证精度及减少运算量的前提下，在0 ～1000 ℃范围内将N 型热电偶热电势分为10 段，利用线性最小二乘法分别得到各区间段的T-E 拟合方程。

拟合公式如式(4)所示，表1 为部分拟合系数和正负最大偏差，分别记为max 和min

正负最大偏差由误差函数G(T)确定，G(T)可表示为式(5)的复合函数形式

表1 N 型热电偶部分拟合系数Tab 1 Part of fitting coefficients of N type thermocouple

其中，T 为理论温度值，F(T)为利用线性最小二乘法分段拟合的函数，f(T)为分度表给定的温度—热电动势(T-E)函数，即为公式(2)所代表的函数。

由于热电偶分度公式和分段拟合的公式均为单调线性多项式，而且在各自分段区间内连续，因此复合函数G(T)在任意分段区间内连续。求导分别得出函数在各连续区间内的最大值与最小值，即正负最大偏差值。为了验证这些数值是否准确，利用Matlab 绘出0 ～1 000 ℃之间各分段的温度差函数G(T)的图形如图2 所示。

图2 理论温度与计算温度的偏差图Fig 2 Deviation chart of theoretical temperature and computational temperature

由图2 可以看出，分段拟合公式已经能够保证偏差小于0.015 ℃，但是由于环境和硬件设备误差等因素的影响，算法在实际应用并不能达到理想的效果，因此，设计了优化算法以满足实际需要，算法在获得某一热电动势值E 后通过查表和多项式计算得出一个温度数值t，那么，这个温度值与真实温度值之间的偏差在区间［min，max］之间，令ta=t+min，tb=t+max，因此，所需确定的温度区间可以表示为［ta，tb］。

需要说明的是，在国际电工委员会ICE584—1 标准中也有由E 转换为T 的公式，但在0 ～600 ℃范围内，该公式计算的误差在［-0.016，0.027］℃之间，在600 ～1 300 ℃的公式误差在［-0.039，0.021］℃之间。由于本文拟合公式分段较多，计算出的误差要小于国标中给出的公式误差，也就是缩小了所需确定的温度区间，为下一步精确计算减小了运算时间。

2.1.2 降低运算复杂度

方程求根等价于求f(x)与x 轴的交点。如果函数单调连续，且在区间两端点的函数值异号，则方程有唯一的解。因此，只要给定一个单调连续，且两端函数值异号的初始区间，即可通过二分法把f(x)的零点所在小区间收缩50%，使区间的两个端点逐步逼近函数的零点，最终以求得方程根的近似值。

在算法设计中，由于二分法需要循环计算公式(2)这类复杂高阶方程，因此，为了降低运算复杂度，利用秦九昭算法简化如下

求公式(6)的值时，首先计算最内层括号内一次多项式的值，然后由内向外逐层计算一次多项式的值，求n 次多项式的值就转换为求n 个一次多项式的值，计算次数可以减少到只做n 次乘法和n 次加法，有效降低了运算复杂度。

2.2 算法流程

图3 所示为算法流程，其过程为:

1)获取经冷端补偿过的热电动势E，查找拟合公式系数表获取分段拟合公式，确定温度t0。

2)根据分段拟合函数值正负最大误差确定二分法查找的起始温度区间［ta，tb］。

3)由公式tc=(ta+tb)/2 算出区间中点tc，判断条件tb-ra＜δ是否成立，如果条件成立，则tc便是所求温度值;否则，判断分度表公式与实际热电势的差值函数函数P(tc)=f(tc)-E是否等于0。

4)如果函数值P(tc)等于0 成立，则tc便是所求温度值;否则，判断其是否大于0，若成立，则令tb=tc;否则，令ta=tc。最后，返回步骤(3)直至求得最佳解。

图3 算法流程图Fig 3 Algorithm flow chart

3 实验结果与分析

算法的仿真测试实验主要包括测温精度测试和运算时间测试。实验是在差示量热扫描仪(热分析仪的一种)上测试的，该仪器以ATmega128 单片机为核心，时钟为16 MHz。

表2 为实验选取的比较有代表性的温度点的温度对照表。其中理论温度为根据分度公式计算的当前热电动势所对应的温度值，测得温度为使用本算法得到的温度值，δ=0.001。由表中数据对比可以看出:使用本算法温度误差小于0.005 ℃，达到了计算的精度要求。不仅如此，本算法可以根据实际需求，通过改变δ 值，减少不必要的程序循环计算过程，提高运算速度。

在同样的硬件平台上对比四种常见算法的实验数据，算法1:查表法;算法2:分段曲线拟合法，即国标中给出的电动势转换为温度的函数(T-E);算法3:传统的方程求根法;算法4:本文提出的结合分段曲线拟合和二分法。4 种算法的温度误差如图4 所示。

表2 理论温度与测得温度对照表Tab 2 Comparison table of theoretical temperature and measured temperature

从图4 可以看出:在0 ～1 000 ℃范围内，本文提出的算法精度可达到±0.005 ℃，计算精度与算法3 的精度相近，远高于算法1 和算法2。

图5 为四种算法所需的计算时间。由图可见，算法1和算法2 运算时间在10 ms 以下，远远低于算法3 和算法4。而算法4 在运算时间上比算法3 快近4 倍。

因此，综合运算时间和精度，本文算法具有运算速度快、计算精度高的优势。

4 结束语

图4 四种算法误差图Fig 4 Error plot of four kinds of algorithms

图5 四种算法运行时间Fig 5 Running time of four kinds of algorithms

本文提出了一种改进的快速高精度热电偶测温算法，以方程求根法为基础，使用最小二乘法和导数定义快速确定查找温度最小误差区间，秦九昭算法简化计算公式，二分法快速收敛求得温度值，克服了传统计算方法的计算精度低和运算时间长的缺点。实现结果显示:在以ATmega128为控制核心，时钟为16 MHz 的硬件平台下，本文算法在0 ～1 000 ℃的温度范围内在达到±0.005 ℃的较高精度的同时拥有相对较快的80 ms 响应速度。

［1］ 吴来杰，严隽薇，刘 敏.基于数值计算的热电偶测温［J］.仪表技术与传感器，2009(5):94-95.

［2］ 王红萍.一种基于基本样条插值的热电偶特性曲线拟合方法［J］.元器件与应用，2000(10):33-35.

［3］ 邓建中.计算方法［M］.西安:西安交通大学出版社，2001.

［4］ 宗殿瑞，任志考，钱 峰.方程求根法计算热电偶测量温度［J］.青岛化工学院学报:自然科学版，2002(2):88-90.

［5］ GB/T 16839.1—1997，第1 部分:分度表.热电偶［S］.

［6］ 瞿江峰.一种基于热电偶的温度测量的线性拟合方法［J］.中国西部科技，2010，26(9):21-23.