基于矢量传感器的空中脱靶量测量方法研究

綦笑微，高洪举，马丽丽，董佳新，宋文利

(中国白城兵器试验中心，吉林 白城137001)

0 引 言

在连续介质声场中，任意一点附近的运动状态可用声压p，密度ρ 及介质质点振速v 唯一表示［1］。声压是标量，振速是矢量，其方向与波到达的方向一致。传统的声学定位系统采用声压传感器阵列，利用信号传播时间延迟确定目标的方位，属于标量测量，没有利用声波的矢量信息。近年来，利用声波矢量场的声矢量传感器技术已经在水声领域开始广泛的重视和探索研究，其具有单阵元定向，方位分辨率高、抑制栅瓣等优点［2］。

现有声学脱靶量测量系统均属于标量测量［3］。如果将矢量传感器技术引入到现有声探测的研究中，可以实现声脱靶量测量的三维矢量定位。要进行矢量测量就需要振速信息，国内现有矢量传感器，主要针对水声测试原理，不适用空气范围内，这样就给直接获取振速带来一定困难。对此本文开展研究，分析声压、振速关系特性，利用现有声压传感器构造了基于压差原理的三维声矢量传感器，提出声压、质点振速联合信息处理的空气声矢量定位思路，采用复声强法利用声压、振速互谱实现了目标的到达方向(direction of arrival，DOA)估计，并通过概率法实现了多基阵的目标声学定位。

1 矢量声学传感器的布阵方案设计

1.1 目标声场声压与振速之间的关系

设声场中某点r 处的声压为p(r，t)，振速为v(r，t)，声源的目标方向为(β，θ)。系统坐标系如图1 所示。对于均匀平面波声场，声学的运动方程［4］

在上式中可以由r 方向上距离为Δr 的相近两点(kΔr≪1，k 为波数)的声压值p1(r，t)，p2(r，t)近似求得振速［5］

1.2 三维声学矢量传感器构建

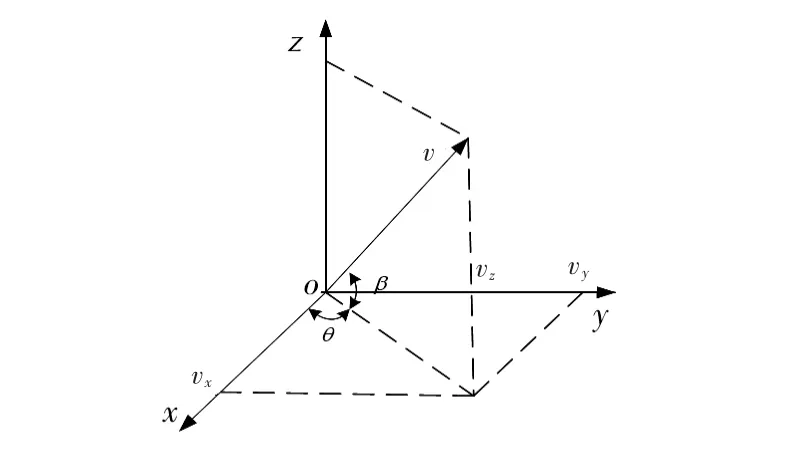
图1 振速及其3 个正交分量的投影图Fig 1 Projection of vibration speed and three orthogonal components

根据式(2)给出的同点声压、振速的关系特性，可以在3 个坐标轴上分别布设2 个近距离声压传感器构建一个基于压差原理的三维矢量传感器，以获取矢量振速信息。三维矢量传感器与被测目标的声源入射方向存在如图2 的位置关系。设目标满足远场条件，矢量传感器在x 轴方向上的阵元记为1，2，接收到的声压分别记为p1(t)，p2(t);y轴方向上的阵元记为3，4，接收到的声压分别记为p3(t)，p4(t);z 轴方向上的阵元记为5，6，接收到的声压分别记为p5(t)，p6(t)。

图2 目标入射方向与矢量传感器位置关系Fig 2 Position relationship between incident direction of target and vector sensor

1.3 空中脱靶量测量布阵设计

现有声脱靶量测量系统采用直线一字型空中吊靶布阵方式，属于二维测量，不能进行三维定位。这样就限制了其试验使用范围。如果采用传统声压传感器进行空间大尺寸布阵，利用几何关系进行结算来确定三维脱靶量坐标，既存在具体布站困难，又存在由于空中扭曲、型变所引起的误差。如果将本文设计构建的矢量传感器进行封装、固化，选取一定数量组成线型阵布设于靶机下面可以实现脱靶量的三维矢量测量，其结果如图3 所示。

2 基于声压与质点振速联合的声矢量波达方向估计

2.1 三维矢量传感器目标定向原理

设矢量传感器各阵元距阵中心o 的距离均为D，信号频率为fo，根据矢量传感器输出的振速的三个分量可得到目标的俯仰角β 和方位角θ

图3 矢量传感器空中脱靶量测量布阵示意图Fig 3 Airy miss distance measurement embattle diagram of vector sensor

由于同一点的声压和质点振速是完全相关的，而其测量噪声是不相关的。因此，可以联合处理每个声矢量传感器测得的声压和质点振速信息，有利于减小噪声的影响，提高声矢量传感器的定向能力。

由于［6］

其中，I 为声强，即取能流密度的时间平均值表示声波能量的强度;T 为平均时间;p 为声压。

可知，声场中同一点处的声强方向与该点处的质点振速方向相同，即每个声矢量传感器处的声强方向也为目标相对于该声矢量传感器的方向。用声场中某点r 处的声强在3 个轴上的分量确定俯仰角和方位角为

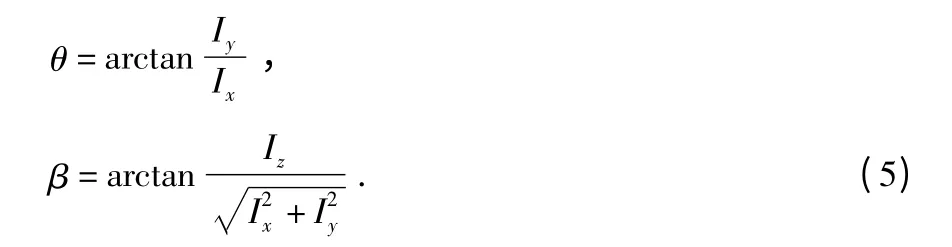
在无干扰的理想情况下，式(3)和式(5)给出相同的结果;在有干扰时，式(5)结果将优于式(3)。

2.2 基于矢量传感器的目标DOA 估计

由于目标信号的声压和振速是相关的，而各种同性环境干扰中声压和振速是不相关的或相互很弱［7］，因此，利用声强来确定波达方向具有良好的抗干扰性。基于平均声强只能用于单目标的方位估计，复声强测向可以分辨频谱有差异的多目标方位，所以，采用声压、振速互谱来测向。

在时域中，声强等于相同时刻声压与振速的相关函数，即

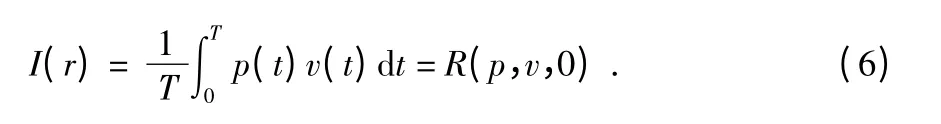
在频域中，与互相关函数相对应的量为互谱密度函数，即

式(7)将时域中的互相关函数转换为频域中互谱密度函数。相反地进行傅里叶逆变换就可经频域互谱密度函数转换为时域对应的互相关函数，即为

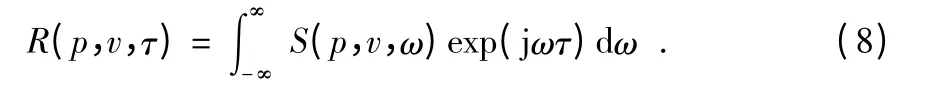
对p(t)和vi(t)(i=x，y，z)作Fourier 变换，得到相应的谱为p(ω)和Vi(ω)，则声压、振速互谱(互功率谱密度函数)为

式中 *表示共轭运算。

将式(8)代入式(6)，有

并根据傅里叶变换基本特性，2 个同相位输入的能量集中在互谱的实部，即可得到原点o 处声强在3 个轴上的分量

式中 po(ω)为原点o 处的声压的Fourier 变换，Vi(ω)为原点o 处的3 个振速分量的Fourier 变换。

下面分别计算po(ω)和Vi(ω):

由于两点连线中点的声压可近似表示为两参考点的平均值，所以，po(ω)可以表示为

对式(2)取Fourier 变换，得

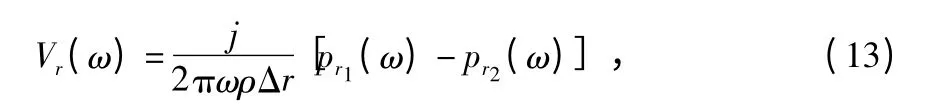
即得到原点o 处的三个振速分量的Fourier 变换。

综合以上分析并代入式(5)可得到目标声源的DOA 估计

3 基于概率的多基阵被动声定位原理

用概率的观点来看，目标位置落在空间不同点的概率密度是不一样的。目标位置落在测量子集上的概率要大一些，落在测量子集以外的区域，距测量子集越远概率越小。多个基阵将形成多个测量子集，目标落在空间某一点的概率就应由多个测量子集对应的多个概率而定。根据分析，在整个空间内总的概率密度函数只有一个峰值，故可以将该峰值对应的位置作为多基阵的定位结果。系统布阵如图4所示，声源坐标为(x，y，z)。

由多种测量误差所形成的实际误差分布呈正态分布，即某个意义的测量ω 的具体测量结果为ω'，可以用ω 的概率密度函数来描述，即

设具体的测量w 对应一个子集，它所给出的坐标点与测量值之间的关系为

下面需通过每个的测量基阵的结果来确定关系式(16)。系统的n 个基阵，其坐标为(xh，yh，zh)，h∈{1，2，3，…，n}，每个单基阵，其测得的目标俯仰角为βh、方位角为θh。这样，对于单基阵h 可以用俯仰角为βh、方位角θh实际估计值为(βho，θho)。假设目标的方位角和俯仰角不相关，其概率密度函数可表示为

将复杂的非线性问题线性化。将(18)式在(x0，y0，z0)((x0，y0，z0)可取几何交叉法的定位结果)附近的区域，采用泰勒级数展开的办法，取一级近似并带回式(17)，经计算得到单基阵定位的概率密度函数可写成

假设基阵与基阵之间相互独立，对于多个基阵联合估计目标位置的情况，其概率密度函数应为单个基阵概率密度函数的乘积。多基阵系统的概率密度函数可写为

求解目标位置的过程为求解概率密度函数最大点的过程。对分别求总概率密度函数的指数F(x，y，z)对X，Y，Z的导数，并令其等于零，由此可得求解目标位置的方程组为

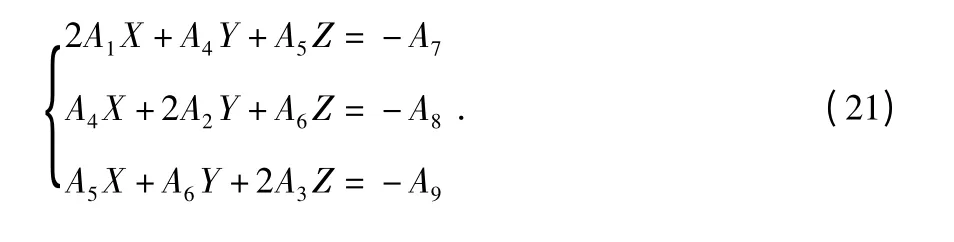
从上式可以看出，当线性方程组的行列式不为0 时，目标位置有唯一解。

图4 多基阵系统布阵示意图Fig 4 Diagram of multi－array system embattle

4 仿真实验与精度分析

采用实测的炮口声音数据，对基于三维压差式矢量传感器复声强测量的目标定位在各种条件下的估计精度进行仿真实验研究。本节仿真实验采用的炮口声信号的采样频率为100 kHz，火炮距离矢量传感器几何中心的距离为1 000 m，空气声速取c=340 m/s。

4.1 不同矢量传感器尺寸时的目标DOA 估计精度

取SNR=30 dB，积分时间取为T=1 s，目标的俯仰角为60°，方位角在-180°～180°之间变化时，不同矢量传感器尺寸R 时的目标方位角估计精度如图5 所示。目标的方位角为45°，俯仰角在0°～90°之间变化时，不同传感器尺寸R时的目标俯仰角估计精度如图6 所示。

图5 不同传感器尺寸时的目标方位角估计精度Fig 5 Target azimuth angle estimation precision with varying size of sensor

图6 不同传感器尺寸时的目标俯仰角估计精度Fig 6 Target pitching angle estimation precision with varying size of sensor

通过仿真可以看出:在一定的信噪比和积分时间下，目标DOA 估计的精度随矢量传感器尺寸的增大先增大，后减小。阵的尺寸为D=0.15 m 时，目标的俯仰角估计精度最高。综合考虑，选取式矢量传感器的尺寸R=0.25 m 时，可以获得最佳的DOA 估计精度。

4.2 不同积分时间时的目标DOA 估计精度

取SNR=30 dB，矢量传感器尺寸取R=0.25 m。目标的俯仰角为60°，方位角在-180°～180°之间变化时，不同积分时间时的目标方位角估计精度如图7 所示。目标的方位角为45°，俯仰角在0°～90°之间变化时，不同积分时间T 时的目标俯仰角估计精度如图8 所示。

图7 不同积分时间时的方位角估计精度Fig 7 Precision of target azimuth angle estimation at different integral times

图8 不同积分时间时的俯仰角估计精度Fig 8 Precision of target pitching angle estimation at different integral times

由实验结果可知，目标方位角的估计精度随积分时间的增大而提高，当积分时间大于0.8 s 时，目标方位角估计的均方根误差小于1°;当积分时间小于1 s 时，目标俯仰角估计精度随积分时间的增大而提高，但当积分时间大于1 s时，俯仰角估计精度有所降低;积分时间大于0.25s 时，目标俯仰角估计精度在1°以内;积分时间为1s 左右，俯仰角估计精度为0.8°。

4.3 矢量传感器空中脱靶量定位精度分析

传统声脱靶量测量系统采用声压传感器构成，测量中没有利用声波的矢量信息，只能进行垂直于入射方向的传感器直线阵列所在平面的二维坐标定位，并且其垂直方向结果是应用水平方向传感器时间差拟和得到的，往往误差很大(最大可能达到十几厘米)。假定声脱靶量测量系统的脱靶量测试靶幅为8 m×8 m。矢量传感器的定向精度为0.8°。就三维定位精度进行简单推算，其可以实现定位误差7 cm 以内的三维坐标定位，这样就大大扩展了其设备的使用范围。

5 结 论

1)基于声压、质点振速联合信息处理的声矢量定位方法，可以实现空气中目标的声学定位。矢量传感器可以用于空中脱靶量测量，可是实现10 cm 以内误差的三维坐标测试。

2)用声压、振速互谱实现目标的方向估计，可以抵消各项同性的噪声干扰，信号不变，从而提高信噪比。

3)由于复声强定向的多目标分辨优势，可以利用矢量传感器来进行多目标的定位、运动目标的轨迹跟踪，并可以开展相关领域的矢量声定位技术研究。

［1］ 赵 微.矢量传感器阵高分辨方位估计及其稳定性研究［D］.哈尔滨:哈尔滨工程大学，2008:2-3.

［2］ 陈丽洁，张 鹏.矢量水听器综述［J］.传感器与微系统，2006，25(6):5-8.

［3］ 綦笑微，张 军.声脱靶量测量系统误差分析［J］.兵器试验，2006(3):67-68.

［4］ 惠俊英，惠 娟.矢量声信号处理基础［M］.北京:国防工业出版社，2009.

［5］ Thompson J K，Tree D R.Finite difference approximation errors in acoustic intensity measurements［J］.J Sound and Vibration，1981，75(2):229-238.

［6］ 蔡宗义，赵俊渭.低频小尺寸高精度空中运动目标定位算法［J］.火力与指挥控制，2008，33(11):148-149.

［7］ 白兴宇.基于联合信息处理的声矢量阵测向技术［D］.哈尔滨:哈尔滨工程大学，2006:11-15.