基于序贯检测的无线传感器网络决策融合算法*

宋晓鸥

(武警工程大学，陕西 西安710086)

0 引 言

无线传感器网络(WSNs)通过节点冗余布置提高整体感知性能和健壮性，但是采集信息的冗余使网络负载随之增加，能量有效又是无线感知网络设计中需要考虑的首要问题，因此，在无线传感器网络采用数据融合算法是必需的［1］。无线传感器网络与有线传感器网络的数据融合存在着极大的差异，其表现在网络的数据通过无线信道的衰减后可能变得无法辨识。针对无线传感器网络运行在衰减信道上的情景条件，国内外学者进行了相应的研究:文献［2］研究了无线传感器网络中衰减信道下的最优决策融合规则，并提出了在性能、耗费资源量和复杂度之间折衷的次优算法。文献［3］利用条件概率密度函数推导了新的融合规则，减少了对信道参数的估计，在不同信噪比情况下提出了次优融合规则。文献［4］研究了在带宽受限的条件下的簇网络结构下的分布式融合问题，簇首节点将接收信息进行简单平均后作出判决。文献［5］采用二进制对称信道考虑由无线通信而引入的错误，提出基于权重平均的分布融合检测算法。这些融合算法在特定条件下均取得了良好的效果，但是，它们的应用场景的设想条件都是参与融合的节点数目恒定，其目标是在参与节点数目固定的条件下实现某一性能指标的最优化。

假设在参与数据融合的节点达到一定数目后，数据融合系统达到预定性能，此时，出于能源管理的角度，剩余节点最好的策略是进入休眠或停止发送，即参与节点的数目应该是可变的。本文引入信号处理中序贯检测(SD)的概念，使参与节点的数目不固定，采用边接收边判决的方式，在衰减信道模型下构建基于序贯检测的无线传感器网络数据融合数学模型。考虑物理层调制解调特性，进一步提出基于序贯检测思想的无线传感器网络数据融合判决(WSNs data aggregation based on sequential detection，WDASD)方法。

1 数据融合系统模型

数据融合从网络拓扑结构上可分为分簇型数据融合、树形网内数据融合、簇树型网内数据融合［6］。无论以哪种网络结构进行，数据融合的最小单元都可归为星形网络。在数据融合的最小单元中，设定有一个汇聚节点和N*个传感器节点。在本文中，假定节点的通信模式为半双工通信，如此，传感器节点与汇聚节点的通信是依次建立的。细化最小单元的工作模式，设定网络的接入采用TDMA，汇聚节点为每个传感器节点分配一个时隙，传感器节点与汇聚节点的依次通信可以描述成数据包的依次到达，构成序列{x1，x2，…，xN}。

文中设定系统模型进行的是决策融合［1］，设想在检测事件发生的场景中，目标区域布置有大量传感器节点，节点感知后，分别做出二元判决“0”或“1”，这些局部判决通过无线传输在融合中心汇集，得到全局判决H0假设和H1假设。此处事件判决过程划分的两种假设检验定义如下:

1)H0:无指定事件发生。

2)H1:有指定事件发生。

为了验证融合决策算法的性能，考虑虚警概率P(H1|H0)、检测概率P(H1|H1)两个指标。此外，无线传感器网络是能量有限的网络［7］，所以，在满足上述两个指标的条件下，系统能量消耗也是必须考虑的一个因素。文献［8］指出，节点发射功率固定时，系统消耗的能量正比于传输的数据量。当传感节点发送的数据包长度一致时，整个系统的数据传输量正比于参与融合的传感节点数目N。因此，本文将N 作为能量消耗的指标。

2 WDASD 算法

序贯检测属于统计检测的一种［9］，其多用于信号检测。Wold 和Wolfwitz 已经证明在给定虚警概率和漏检概率的情况下，序贯检测所需的平均观测次数是最小的［9］。假设传感器处在理想的工作环境，即传感器可以准确判决事件的发生与否，那么多个传感器的观测判决结果经过无线信道后，在融合中心处依次汇聚成数据序列，整个系统引入的噪声为无线信道噪声。此时，可以将判决过程建模为序贯检测问题，其中观测次数相当于汇聚节点接收的传感数据包的数目。因此，在给定指标的情况下，应用序贯检测理论的事件判决方法所需的平均参与节点数目最小，即传输数据量最小，系统能耗最小。下面具体分析基于序贯检测的传感器节点传输数据融合的判决过程。

假设，当第N 个传感器节点与汇聚节点的传输完成时，汇聚节点处获得了N 个观测信号采样序列［x1，x2，…，xN］T，将这个N 维随机矢量映射到观测空间Φ 中的一个点。判决域分布如图1 所示，它们满足

图1 序贯检测的判决域Fig 1 Decision domain of sequential detection

3 结合物理层和无线信道特性的判决方法

3.1 问题描述与判决方法

选择2FSK 作为物理层调制方式进行分析，解调采用同步检测法，模型［10］如图2 所示。解调时分上下两条支路，采用两个带通滤波器区分中心频率分别为f1和f2的信号，在经过相干解调后，送入抽样判决器。

图2 2FSK 信号采用同步检测法性能分析图Fig 2 2FSK performance analysis using synchronization detection method

假设发射端发送的是“1”信号，此时比较的两路输入波形分别为:

上支路

下支路

式中 a 为信号成分;n1c(t)和n2c(t)均为低通型高斯噪声，其均值为0，方差为

发送的信号为“0”信号时，两路输入波形分别为:

上支路

下支路

同步检测法中输出的结果由抽样比较器得出，定义变量z 为

z 为高斯随机变量，接收信号为“1”时。均值为a，方差为;接收信号为“0”时，均值为(－a)，方差为

进一步考虑无线通信信道中的衰落，可设

其中，Ploss为路径损耗，Pt为发射功率，Pr为接收功率。对于每个传感器节点，其与汇聚节点之间的信道的路径损耗基本不变，可以当作恒参信道。设发射功率始终维持不变，对于第i 个传感节点，其参数ai始终维持不变。

根据物理层性质，可构建二元数据通信系统的假设模型，两个假设下的汇聚节点处的观测信号分别为

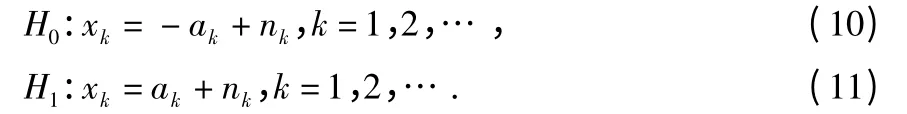
其中，观测噪声nk是均值为0、方差为的高斯噪声。ai为固定值序列{a1，a2，…，aN*}，其中，N*为系统中传感节点的总个数。

若进行到第N 次接收，则似然比函数为

对数似然比函数为

判决表达式可以表示为

将这种基于序贯检测的无线传感器网络数据融合判决方法简称为WDASD。

3.2 似然比检测门限的求值

设P(H1|H0)和P(H0|H1)的约束值分别为

根据P(H1|H0)和P(H0|H1)的定义，有

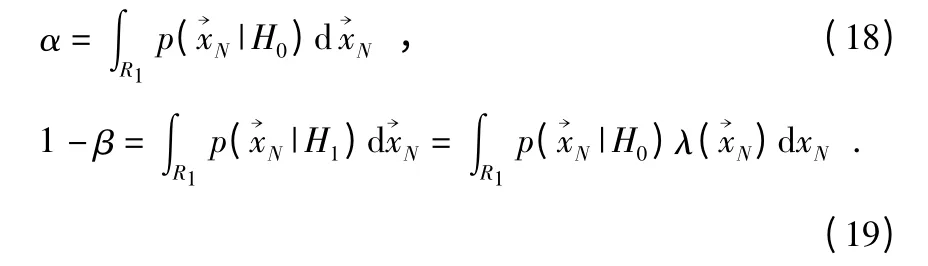
H1为真的条件下判决假设H1成立时，需满足λ(xN)≥η1，代入式(19)，有从而有不等式

又因为信号的序贯检测的条件是，当似然比函数λ(xN)≥η1时，判决假设H1成立，所以，只有取η1的理论值上限，似然比检验时才能有足够的观测数据个数以满足性能指标。此时，检测门限η1的设计公式为

同理，可得

当ln η0＜ln λ(xn)＜ln η1时，汇聚节点不作出判决。而无线传感器网络中的节点是有限的，因此，定义能参与融合的传感器节点的最大数目为N*，当参与的节点数目达到上限时，转为固定节点数目的数据融合，强制做出判决。

3.3 仿真实验

如第2 节所述，检测概率和虚警概率是数据融合需要的指标。通过仿真实验对上述指标进行验证。首先，假定各传感器节点到汇聚节点的信道条件一致，设a 序列为1 序列，信噪比为，即0 dB。最小单元内传感器节点的总个数为100，设P(H1|H0)和P(H0|H1)的约束值均为0.01，仿真结果如图3 所示。

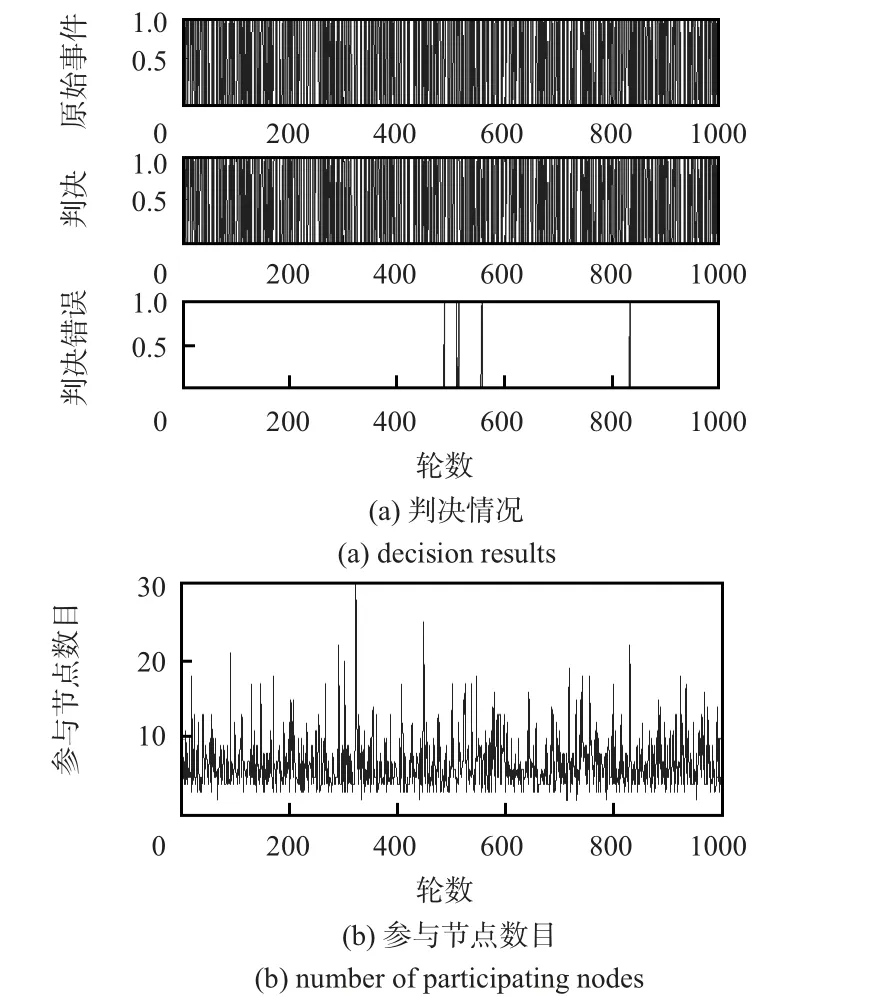
图3 信参一致条件下WDASD 算法Fig 3 WDASD algorithm under condition of the same channel parameters

图3 (a)展示了相应于发生事件的最终判决，1 000 次判决中判决错误总数为5，满足错判概率的约束值要求，算法达到预期性能。另一方面，由图3(b)可见，由于噪声的不重复性，参与节点数目不定，从2 个至30 个不等，其平均值为6.561 0。其中，噪声方差越大，参与节点数目上下波动越大、平均值越大。

在现实环境中，受随机布置和地形环境等条件影响，信道条件很难达到一致。假设汇聚节点接收到的信号的强度在［0，1］区间内均匀分布，汇聚节点处噪声方差为，进行仿真，结果如图4 所示。

图4 不同信参条件下的WDASD 算法Fig 4 WDASD algorithm under conditions of different channel parameters

由图4 中信道参数一致和不一致两种情况对比可知，信参不一致时融合判决的质量较低，表现在参与的节点数目较多，且曲线上下波动较大。在此基础上，考察信道参数的不同排列对平均参加节点数目的影响，仿真时，对a 进行50 次随机分布参数，每次分布参数后进行1000 轮融合判决，取其平均参与节点数目，结果如图5 所示。

图5 各信道参数随机排列时WDASD 算法Fig 5 WDASD algorithm while each channel parameter is randomly arranged

由结果可见，不同参数分布对平均参与节点数目的影响较大，究其根本原因，主要是因为不同信道参数分布下汇聚节点处收到的传感器节点的信号的衰减不同，导致信噪比不等。而本文提出的WDASD 算法的本质是一种根据信号统计分布特性进行加权的判决算法，信噪比大的信号能提供更大的信息量，所以，不同信噪比的信号到达顺序对算法性能有着较大影响。

4 结束语

本文从减少网络中最小融合单元中参与融合的节点数目角度出发，对无线传感器数据融合问题进行建模，将序贯检测的思想应用于数据融合判决中，提出了WDASD 算法，并对其进行了仿真实验。实验表明:算法性能良好，能在满足系统要求的条件下使参与节点数目减少，进而降低了系统整体功耗。

［1］ 陈正宇，杨 庚.无线传感器网络数据融合研究综述［J］.计算机应用研究，2011，28(5):1601-1604.

［2］ 李燕君，王 智，孙优贤.资源受限的无线传感器网络基于衰减信道的决策融合［J］.软件学报，2007，18(5):1130-1137.

［3］ 戎 舟，王锁萍.基于衰减信道的无线传感器网络［J］.仪器仪表学报，2010，31(11):2622-2628.

［4］ Luo Z Q.Universal decentralized detection in a bandwidth constrained sensor network［J］.IEEE Transactions on Signal Processing，2005，53(8):2617-2624.

［5］ Tian Q，Coyle E J.Optimal distributed detection in clustered wireless sensor networks:The weight median［C］∥Proc IEEE INFOCOM，2006:562-568.

［6］ 屈剑锋.无线传感器网络数据融合与目标跟踪研究及其应用［D］.重庆:重庆大学，2007:33-34.

［7］ 回春立，刘 巍.无线传感器网络中的数据融合及其能效评估［J］.计算机应用研究，2008，25(2):546-550.

［8］ Heinzelman W R，Chanddasan A.Balakrishnan H.Energy-efficient communication protocol for wireless microsensor networks［C］∥Proc Hawaii International Conference on System Sciences，Maui，2000:1-10.

［9］ 赵树杰，赵建勋.信号检测与估计理论［M］.北京:清华大学出版社，2005:104-108.

［10］樊昌信，曹丽娜.通信原理［M］.4 版.北京:国防工业出版社，2009:201-203.