一种新型微力传感器设计

章晓明，刘晓东，班 炯，陈靖宇，顾小稳

(1.上海航天控制技术研究所，上海200233;2.同济大学 机械与能源工程学院，上海201804)

0 引 言

微力传感器是微传感器的一种，而微传感器的体积小、功耗低，便于和信号处理部分集成以构成微传感器测试系统，这些特性使其可以应用于汽车、航空航天、电机、医学、环境监测等广阔领域。微力传感器是最早开始研制的微机械产品，也是微机械技术中最成熟、最早开始产业化的产品，其原理是将力转换成电信号输出［1］。

目前微力传感器的量程范围小且灵敏度低，很难对更加微小的力进行测量［2］。同时在进一步提高灵敏度的过程中，会遇到非线性度随着灵敏度的提高变差、灵敏度提高、稳定性变差等问题［3］。

本文利用电阻应变原理，设计了一种微力传感器，该传感器采用柱式结构，灵敏度可达0.057 5 V/N，适用于微力测量，能保持较好的线性度，静态特性良好。

1 微力传感器结构

微力传感器的工作原理是电阻应变片发生变形时，其电阻值发生变化，柱式结构对压应变尤为敏感，纵向应变测量精度高，此传感器选用立柱结构［4］，如图1 所示。

图1 传感器结构图Fig 1 Structure diagram of sensor

2 弹性元件的有限元分析

微力传感器的灵敏度和量程直接相关，需对传感器结构进行受力分析，用弹性元件的单位应变表征传感器的灵敏度，固有频率表征量程。

对传感器的弹性柱体进行静力分析和模态分析，主要物理参数为弹性柱体的形变量和固有频率［5］。

静力分析用于计算固定不变的载荷和响应作用于结构或部件上引起的位移、应力、应变和力，忽略惯性和阻尼效应的影响［6］。传感器承受纵向外力发生形变，通过静力分析求解纵向应变量，传感器应变云图如图2 所示。

图2 传感器静力分析应变云图Fig 2 Strain cloud diagram of static force analysis of sensor

模态分析用于研究结构的振动特性，即固有频率和振型。固有频率表征结构刚度，振型表征结构在某个方向的变形趋势，传感器模态分析的纵向振型云图如图3 所示。

图3 传感器模态分析纵向振型云图Fig 3 Cloud diagram of longitudinal vibration type of modal analysis of sensor

利用ANSYS 进行有限元分析前处理相关参数如表1所示，对传感器进行静态分析和模态分析的求解结果如表2所示。

表1 有限元分析前处理相关参数Tab 1 Related parameters of finite element analysis pre－processing

表2 有限元静力分析和模态分析求解结果Tab 2 Solution of static and modal analysis of finite element

3 传感器静态特性

测量装置的静态特性是在静态测量情况下描述实际测量装置与理想线性系统的接近程度，通过静态标定实现［7］。传感器的静态标定是基于单一变量原则，利用标准设备产生已知的标准量，或用基准量来确定传感器输出量和输入量之间关系的过程［8］。传感器的静态特性必须在静态标准条件下进行标定，传感器的静态特性指标主要有线性度、重复性、灵敏度和回程误差，其中灵敏度和线性度是传感器最重要的性能特征［9］。

静态标定所用主要实验装置为YD—21 电阻应变仪和研华PCI—1711UL 数据采集卡。传感器静态标定实验原理图如图4 所示。

图4 传感器静态标定实验原理图Fig 4 Principle diagram of static calibration experiment of sensor

将砝码置于传感器上，应变电桥输出相对应的电压，应变仪进行信号调理，采集卡采集电压信号，通过串口传输至计算机，上位机以LabVIEW 为平台，实时显示采样得到的传感器信号，并将数据存至EXCEL。传感器静态标定的指标如表3 所示。

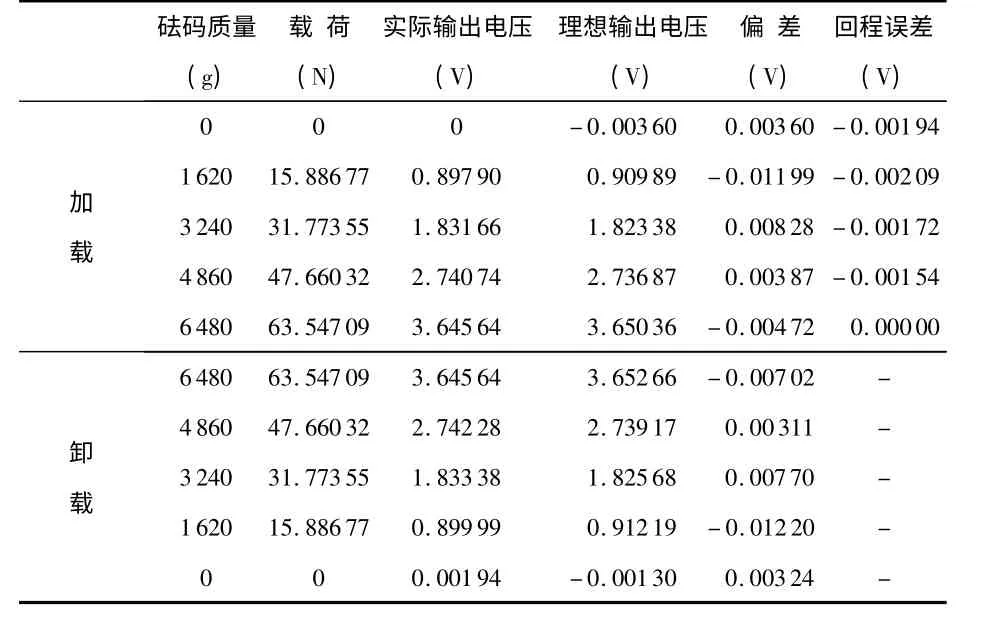
表3 传感器静态指标标定Tab 3 Static calibration of sensor

样本数据表示为X，取容量N=1 000。虽然目前国内外传感器的标定尚无统一标准，但数据处理总体方法和理论依据是一致的，一般取样本的算术平均值作为该整体的均值估计量［10，11］，传感器加载曲线和卸载曲线分别如图5所示。

图5 传感器静态标定拟合曲线Fig 5 Fitting curve of static calibration of sensor

利用最小二乘法对加载曲线和卸载曲线线性拟合，得到加载曲线拟合表达式

卸载曲线拟合表达式

采集卡参考电压为5 V，故传感器最大电压输出量取为5 V，则传感器静态指标如表4。

表4 传感器静态指标Tab 4 Static indicators of sensor

4 误差分析

随机误差是在重复测量中按不可预见的方式变化的测量误差的分量，其参考值是对同一被测量进行无限多次重复测量所得的平均值，随机误差等于误差减去系统误差。测试系统测试实验中，近似认为传感器静态指标的随机误差服从正态分布［12］。

利用正态分布假设和最大似然估计法，对传感器静态指标的随机误差进行统计分析。传感器静态指标的随机误差统计分析参数如表5 所示。

表5 传感器静态指标的随机误差统计参数Tab 5 Random error statistics parameters of static indicators of sensor

5 结 论

1)设计了新型微力传感器的结构，并对其弹性元件进行了有限元静力分析和模态分析，传感器弹性柱体的纵向应变量高于一般的力传感器，灵敏度较高，适用于微力测量;固有频率远高于常见的外部动态力频率，几乎不会发生共振现象。

2)对微力传感器进行了静态标定，标定的静态指标表明该传感器加载特性和卸载特性几近一致，保持了较好的线性度;静态特性良好。

3)对传感器的静态指标的随机误差进行的分析表明:传感器的随机误差离散度小，传感器静态特性稳定，抗干扰能力强。

［1］ 张志禹，于文革.一种新型FBG 微力传感器［J］.传感器与微系统，2014(3):71-75.

［2］ 孙圣和.现代传感器发展方向［J］.电子测量与仪器学报，2009，23(1):1-10.

［3］ 董大为.中国传感器发展应用状况分析［J］.射频世界，2010(3):54-57.

［4］ 马炳辉，卢泽生.小型微力传感器的研制［J］.机械工程学报，2006(5):227-229.

［5］ 张洪信.有限元基础理论与ANSYS 应用［M］.北京:机械工业出版社，2006.

［6］ 李 霞，宋海堂.ANSYS 在机械设计中的应用［J］.计算机技术应用，2007(11):45-46.

［7］ Wang Jili，Jiang Li，Liu Hong.Auto static calibration of multi-axis force sensor based on triaxial accelerometer［J］.Chinese Journal of Scientific Instrument，2008(29):432-435.

［8］ 董健康，韩庆奎.线性压力传感器的静态标定［J］.天津大学学报，1996，29(5):709-715.

［9］ 郑玮玮，刘学观，赵光霞.微压力传感器参数设计及灵敏度分析［J］.仪表技术与传感器，2011(7):15-17.

［10］王志胜，王道波，蔡宗琰.传感器标定的统一数据处理方法［J］.传感器技术，2004，23(3):46-47.

［11］关石菡.数理统计在数据分析中的应用研究［J］.林区教学，2011(6):87-88.

［12］廖念钊.互换性与技术测量［M］.北京:中国质检出版社，2012.