基于正六边形区域划分的无线传感器网络动态目标跟踪*

杨春曦，孙 超，黄 剑

(1.昆明理工大学 化学工程学院，云南 昆明650500;2.华中科技大学 自动化学院，湖北 武汉430074)

0 引 言

作为无线传感器网络(WSNs)的基础应用之一，目标跟踪问题受到了越来越多的关注。由于节点在能量、带宽、通信能力和计算能力等方面的局限性以及跟踪目标的动态性特点，无线传感器网络的目标跟踪系统需重点考虑节点的合理调度，在满足跟踪精度的前提下，降低节点能量消耗，以实现网络寿命的最大化。

近年来，很多学者先后提出了多种协作目标跟踪方法［1～5］。Zhao F 等人［1］提出的信息驱动传感器查询(information-driven sensor query，IDSQ)算法是其中较为典型的协同算法之一。Xiao W D 等人［2］以能量消耗和跟踪精度为性能指标提出了自适应节点调度方法。文献［3］在自适应节点调度算法的基础上为提高目标跟踪的实时性，提出了动态分簇的概念。文献［4］利用集中式卡尔曼滤波器预测目标位置，并唤醒目标周围最近传感器节点工作，但该算法需要性能很高的中心融合节点。文献［5］针对集中式目标跟踪的不足，提出了一种分布式动态一致目标跟踪算法。

目前绝大多数的协同跟踪方法都是建立在动态成簇的基础上，绝大部分都没有考虑到能耗的均衡性。本文提出了一种能量均衡消耗的目标跟踪算法，该算法以正六边形网格作为静态分簇模型，为均衡簇内节点能量消耗，引入虚拟簇头这一概念，通过自适应动态簇头选举，有效地均衡了节点的能量消耗。

1 能量均衡的目标跟踪算法

为不失一般性，本文采用了能实现检测区域重复覆盖面积最少的正六边形网格来划分区域。同时，为确保无线传感器网络的全覆盖和节点间通信的要求，正六边形网格的划分需满足其中，Ro为正六边形网格外接圆半径，Rs，Rc分别为传感器节点的感知半径和通信半径。网格划分完成后，针对无线传感器网络特点，先对传感器节点作如下设定:

1.1 一些假设

1)网络中的所有传感器节点随机等密度分布。

2)网络部署完后，所有节点处于静止状态，初始能量在闭区间［Emin，Emax］内随机分布。

3)节点处于休眠状态时的能耗忽略不计。

1.2 无线传感器网络的建模

1.2.1 网络初始化

当节点部署完毕后，各节点根据预先播撒的信标节点确认自己的坐标，并根据存储在记忆单元中的虚拟单元格信息确认自己所在的簇，然后向周围可通信范围内的其他节点广播自己的ID 标号。这样，网络中所有的传感器节点都能根据接收到的信息获得簇内成员的信息和相邻簇的信息。

1.2.2 簇头节点选举

网络初始化完成后，在各簇中随机选取一个节点作为簇头，且为避免频繁的簇头节点选举，假设目标从进入其检测区域到离开为一个选举周期。当一轮新的簇头选举触发，所有簇成员节点将其剩余能量信息连同目标状态一起发送给簇头节点，剩余能量较高者作为新的簇头节点。

1.2.3 簇头间信息交接机制

当前簇头由扩展卡尔曼滤波算法［7］预测目标下一时刻位置，如果预测位置位于当前簇的边界，该簇头节点就激活其附近邻居簇头节点并把当前信息发送出去。同时，考虑到目标有可能在两相邻簇边界区域来回活动，如图1(a)所示。这时，由于簇头节点的频繁切换，必然会导致整个系统的不稳定。为此，本文提出重叠区域的同时监测，如图1(b)所示，Ro，Ri分别表示各正六边形的外接圆半径和内接圆半径。仍考虑目标从B 区域进入A 区域，当目标位于A，B 外接圆重叠部分(图1(b)中阴影部分)时，区域B簇头节点唤醒区域A 簇头节点，且区域B 节点继续跟踪目标，直到目标离开区域B 外接圆区域并进入区域A 内接圆内时，区域B 全部节点转为休眠状态。

1.3 簇头选举改进算法

在1.2.2 小节中，簇头节点的选举概率只与节点的能量信息有关。由于各节点的初始能量不同，且簇内节点至簇头节点的距离差异较大，势必会造成节点能量消耗的不均衡。如图2 所示，节点A，B 至当前簇头的距离分别为R1，R2，能量分别为E1，E2，且能量和距离满足E2≫E1，R2＞R1。

图2 簇中节点通信关系图Fig 2 Communication relationship between nodes in clusters

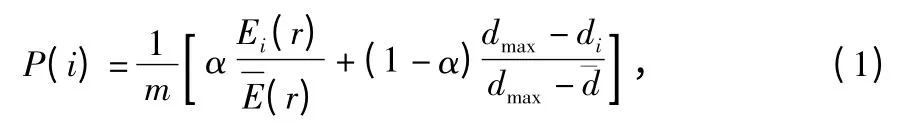
1.4 目标跟踪算法

如果所有任务传感器节点将获取的目标信息发送给簇头节点，由簇头节点来完成全局状态估计，可得簇内集中式扩展卡尔曼滤波(C-CEKF)算法，该算法由于利用了所有传感器的全部观测信号，其估计是全局最优的，但簇头节点的计算量较大，容易产生丢包和时延。文献［8］在此基础上提出了簇内分布式扩展卡尔曼滤波(C-DEKF)算法

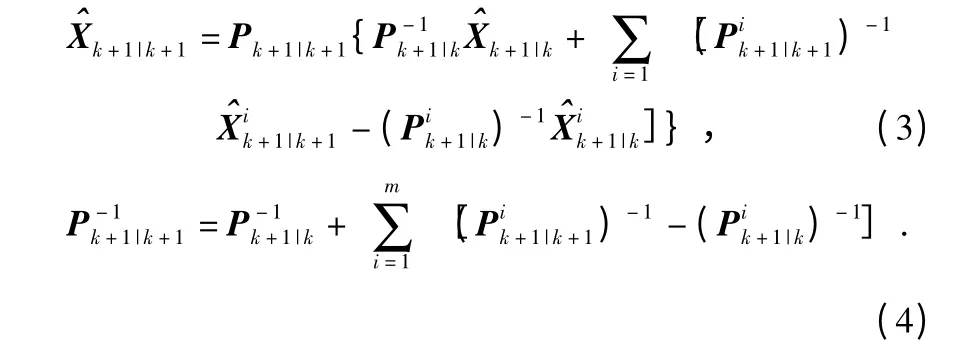
该算法降低了对簇头节点的性能要求，且提高了系统的健壮性。这里，为进一步降低簇头节点的计算复杂度，提出簇内加权分布式扩展卡尔曼滤波(C-DWEKF)算法。设)是对n 维随机变量Xk的m 个无偏估计，且估计误差和误差协方差矩阵分别为

在给出结论前，先给出如下定义:

定义1［9］:若状态估计量为真值X 的最优估计，须满足以下两个条件:

因此

式(11)的值越小，融合的值越准确，于是问题归结为

由于误差协方差矩阵Pk|k具有表明滤波精度的性质。Pk|k的值越小，则对应传感器节点的估计精度越高。可以为其分配其较大的权系数。因此，取各局部状态估计的动态加权系数为

此时最优估计的均方误差

2 仿真与分析

2.1 仿真实例

例1:考虑500 个传感器节点随机均匀布置在50 m×50 m的检测区域，同时该检测区域被划分为72 个外接圆半径为Ro=3.8 m 的正六边形。所有传感器节点的通信半径为Rc=13.7 m。目标运动的离散线性化状态方程为Xk+1=AkXk+BWk。其中，状态矢量Xk=［xkykvx，kvy，kωk］T，这里(xk，yk)，(vx，k，vy，k)和ωk分别是目标的位置、速度和角速度;状态转移矩阵为

式中 T 为采样周期，B=diag［1 1 1 1 1］。Wk∈(0，Qk)是具有均值为零，方差为Qk=1 的高斯白噪声。初始状态X0=［20 10 10 10 0］T，P0|0=10×diag［1 1 1 1 1］T。通过对目标进行100 步跟踪来比较以上三种簇内信息融合算法的性能，评价指标为:

1)跟踪精度

本文给出三种算法位置方向的跟踪精度Φk=。其中和分别表示X 和Y 方向的跟踪误差。仿真结果如图3 所示。

图3 三种算法跟踪误差比较图Fig 3 Comparison of tracking error of three algorithms

从图3 中可以看出:本文中的C-DWEKF 算法具有与其他两种算法相当的估计性能。

2)计算复杂度

现以算法在实现运行时的时间(CPU time)来间接刻画以上三种算法的计算复杂度，并以计算复杂度压缩比

由表1 可以看出:对于C-CEKF 算法簇头节点需要计算高维矩阵的逆，计算复杂，处理时间较长。而C-DEKF 算法由于采用分布式结构，簇内成员节点都对信息进行了一次预处理，降低了簇头节点的计算量，其CPU 运行时间有所降低。进一步，C-DWEKF 算法相对C-DEKF 算法只对各簇内节点的局部估计值做加权处理，计算简单。

表1 三种算法的计算时间与计算复杂度压缩比对比表Tab 1 Comparison sheet of calculation time and calculation complexity compression ratio of three algorithms

2.2 能耗分析

不失一般性，这里也采用文献［10］中给出的能耗模型。在仿真中取:l=5 000 bit，Eelec=50 nJ/bit，εamp=100 pJ/bit/m2，EDA=5 nJ/bit/signal，c=4。下面针对簇头选举改进算法(算法1)和未改进算法(算法2)，从能量消耗角度做一个分析比较。为了便于比较，统计各虚拟单元格内所有传感器节点剩余能量之和。仿真结果如图4 所示。

在图4 中，只统计了跟踪移动目标的20 个簇在200 步迭代后的剩余能量情况。可以看出，本文算法在簇头选举过程中，同时考虑了距离和剩余能量两个因素，减少了簇成员节点与簇头节点的通信距离，在一定程度上节省了很大一部分能量。

图4 两种算法能量消耗对比Fig 4 Comparison of energy consumption of two algorithms

接下来，为了验证本文中改进算法比未改进算法能更有效均衡节点能量消耗，随机选取一个网格并统计网格中各节点的能量消耗情况。网格中节点的分布和能量消耗如图5 所示。

图5 两种算法下单个簇节点能量消耗对比Fig 5 Comparison of energy consumption single cluster nodes of two algorithms

从图5 可以看出:对于未改进算法(算法1)，当算法迭代150 步后，节点3，5，6 的能量已经耗尽，而其他节点的能量还保持在较高的水平。相比之下，对于改进算法(算法2)，由于节点2，3，5 能量较高且距离虚拟簇头较近，因此，在初始阶段有较多的机会当选簇头，从而其能量消耗较快。当迭代超过100 步后，这三个节点的能量与距离综合性能指标下降较快，故当选簇头的机会减少，因而，能量消耗变慢;节点7，9 距离虚拟簇头较远，在前150 次迭代中几乎没有当选过簇头，其能量一直保持在较高的水平;当算法迭代到150 步后，簇内所有节点的能量不仅没有耗尽，且各节点的能量消耗相对均衡。

3 结 论

本文提出了一种基于正六边形网格划分的能量均衡消耗的目标跟踪动态协同自组织算法。该算法在目标跟踪过程中，能动态地唤醒无线传感器网络中合适的簇检测目标并执行C-DWEKF 算法，实现对目标的精确跟踪。与CCEKF 和C-DEKF 算法相比，所提出的算法不仅具有相当的估计性能，而且能够有效降低对单个节点的性能要求，提高系统的健壮性。为进一步平衡簇内节点的能量消耗，特地引入了虚拟簇头的概念，使得该改进算法能根据各簇内节点离虚拟簇头的距离和剩余能量信息自适应动态选举簇头，从而达到均衡各簇中节点能量消耗，有效延长网络寿命的目的。

［1］ Zhao F，Shin J，Reich J.Information driven dynamic sensor collaboration［J］.IEEE Signal Processing Magazine，2002，19(2):61-72.

［2］ Xiao W D，Wu J K，Xie L H.Adaptive sensor scheduling for target tracking in wireless sensor networks［C］∥Proceedings of SPIE，Chongqing，2005:104-112.

［3］ Liu Y G，Xu B G，Feng L F.Distributed IMM filter-based dynamic-group scheduling scheme for maneuvering target tracking in wireless sensor networks［C］∥Proceedings of the 2nd International Congress on Image and Signal Processing，Tianjin，2009:3832-3897.

［4］ 龙 慧，樊晓平，刘少强，等.无线传感器网络动态协作最近邻目标跟踪算法［J］.传感器与微系统，2012，31(7):135-139.

［5］ 龙 慧，樊晓平，刘少强.分布式动态一致性非线性目标跟踪策略研究［J］.计算机应用研究，2013，30(5):1365-1369.

［6］ Li B，Wang Q D，Yang Y M.Optimal distribution of redundant sensor nodes for wireless sensor networks［C］∥Proceedings of the International IEEE Conference on Industrial Information，2006:16-18.

［7］ Kalman R E.A new approach to linear filtering and prediction problems［J］.Transaction of ASME Journal of Basic Engineering，1960，82:35-45.

［8］ Hashemipour H R，Roy S，Laub A J.Decentralized structures for parallel Kalman filtering［J］.IEEE Transactions on Automatic Control，1988，33(1):88-93

［9］ 贾沛璋，朱征桃.最优估计及其应用［M］.北京:科学出版社，1984.

［10］Heinzelman W B，Chandrakasan A P，Balakrishnan H.An application-specific protocol architecture for wireless micro sensor networks［J］.IEEE Transactions on Wireless Communications，2002，1(4):660-670.