一种对称斜置式四陀螺惯导冗余配置方案*
程建华,董金鲁,陈岱岱
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨150001)
0 引 言
余度技术是现代容错技术用于提高惯性导航系统可靠性最常采用的技术之一[1~3]。系统级冗余和器件级冗余是最常用的余度技术[4,5],在过去的几十年里,系统级冗余有许多成功的应用案例,例如:前苏联的东方号、联盟号飞船就采用两套冗余惯导系统,一套为安装于一级仪器舱的平台式惯导系统,另一套为安装于二级仪器舱的捷联式惯导系统[6],但其体积、重量随着冗余数量的增加而成倍增加。对于捷联式惯导系统,可使用器件级余度技术,即通过增加惯性测量元件(陀螺仪或加速度计)的个数进行冗余配置来实现余度技术,从而达到提高系统可靠性和容错能力的目的。例如:美国Honeywell 公司基于正十二面体结构,设计了基于6 个激光陀螺构成的冗余式惯导系统,大幅提升了系统的可靠性,并应用于波音777 飞机[7]。美国航天局将4 个呈锥形安装的陀螺仪应用于EOS—AQUA 卫星[8]。国内,第三代航天器的核心部件也采用了多余度的设计方案。
对于舰船惯导系统,由于惯性器件自身体积较大,单纯通过增加惯性器件数目虽然能提高系统可靠性,但同时也大大增加了惯导系统的体积、重量等。因此,研究惯性器件较少情况下的可靠性提升方法,对于舰船捷联式惯导系统,具有重要的实际意义。
基于此,本文针对四陀螺配置的冗余式捷联惯导系统方案,在分析和验证冗余优化准则性能的基础上,设计了一种基于对称式配置方案的冗余式捷联惯导系统方案,并通过可靠性和精度分析,对方案的有效性进行验证。
1 冗余优化准则等价性
对于采用n 个单自由度陀螺仪的捷联惯导系统,陀螺仪的量测输入可由方程(1)表述[9]

式中 m 为n×1 维惯性测量矢量;H 为n×3 维配置矩阵;X 为3×1 维待求矢量;η 为n×1 维测量噪声矢量。
设测量噪声η 为零均值、方差为σ2的高斯白噪声,其统计特性为

其中,In为n×n 单位矩阵。
根据线性最小方差理论,可以求出捷联惯导导航解算输入X 的估计值

同时,基于式(2)可得到相应的估计误差协方差矩阵为
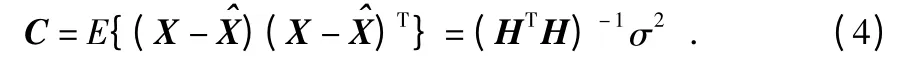
定义导航特性的最优准则为

由式(5)可知,J 是估计协方差矩阵迹的最小值,只与配置矩阵H 和误差方差σ2有关。
根据文献[4]可知,J=min{trace(C)}等价于

即当配置矩阵满足式(6)时,J 取估计协方差矩阵迹的最小值。
式(6)所示的最优准则可采用其他参数进行表征。设噪声η 为零均值高斯白噪声,相应的概率密度函数为[10]
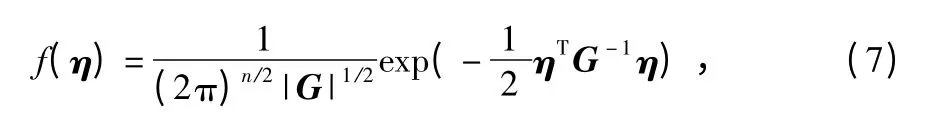
式中 G=(HTH)-1,η 的轨迹满足

K 为放大因子,式(8)表示一个椭球族,给定一个K 值,即可得到一个固定的椭球,相应的椭球体积可表示为

对于式(9),体积V 越小,则噪声η 产生的误差就越小,从而系统的导航特性就越好,定义最优准则为

F 取值越小,噪声η 产生误差的椭球体积就越小,当满足式(6)所示的条件时,F 取最小值,即噪声产生的误差的椭球体积最小,则系统的导航特性最优。从式(5)、式(6)和式(10)可知,当配置矩阵H 满足式(6)时,式(5)和式(10)均取最小值,因此,本文中所提到的两种优化准则在数值运算上等价。
2 冗余配置方案可靠度
在计算系统可靠度时,通常先做如下假设:
1)冗余配置采用单自由度陀螺仪,且只考虑陀螺仪发生故障,可靠度为e-λt,记为R(t)[11];
2)各陀螺仪等概率发生故障,且相互独立。
单个陀螺仪的可靠性表达式为

其中,λ 为故障率,则单个陀螺仪的平均无故障时间(mean time between failures,MTBF)为

对于无冗余系统,其可靠度为

对应MTBF 为

由式(11)~式(14)可知,当系统没有冗余时,系统的可靠性很低(仅考虑陀螺仪发生故障),仅为单个陀螺仪的1/3。
3 冗余配置方案性能分析
图1 给出了三种最常见的四陀螺冗余配置方案分别是:正交配置方案、斜置配置方案、圆锥配置方案。

图1 四陀螺冗余配置示意图Fig 1 Diagram of redundancy configuration of four gyros
对于图1(a)所示的正交配置方案,可推得其陀螺仪量测方程为
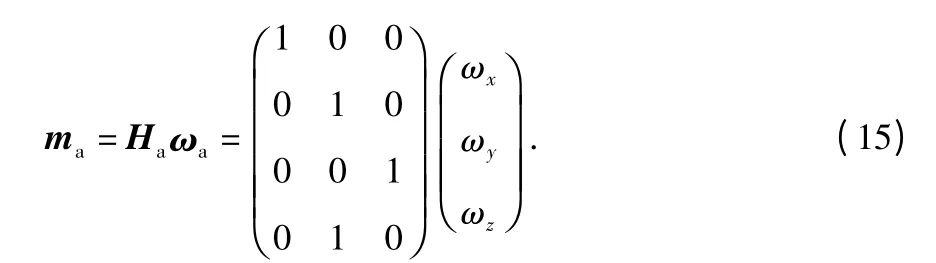
其中,ma=[m1m2m3m4]T为测量值,ωa=[ωxωyωz]T为角速率待求值,Ha为配置矩阵。
对于图1(b)中的斜置方案,其3 个陀螺仪为正交安装方式,最后一个测量轴与前3 个测量轴等夹角安装,即α=β=γ=54.73°。由配置方案可推得陀螺仪量测方程为
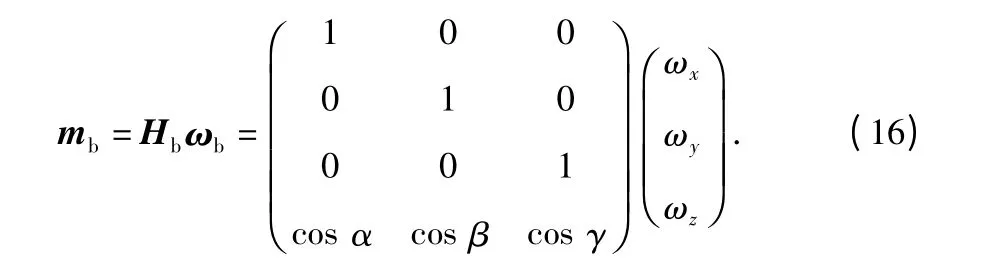
对于图1(c)所示的圆锥配置方案,4 个陀螺仪的测量轴均匀分布在圆锥面上,圆锥的半圆锥角为α=54.73°,且测量轴分别分布在xoz 平面、yoz 平面、-xoz 平面、-yoz 平面上。由配置方案可推得陀螺仪的量测方程为
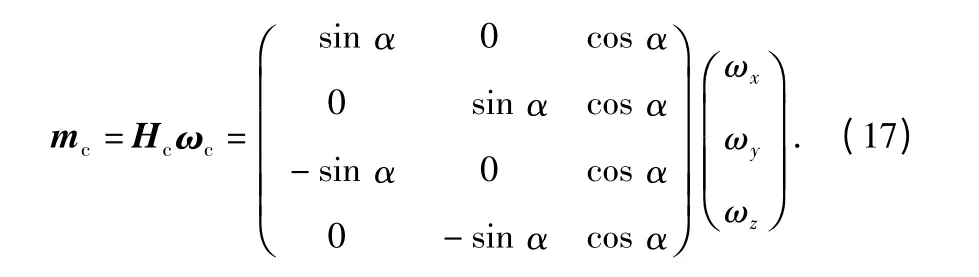
3.1 导航性能比对
根据各夹角,可得出图1(b),(c)方案具体配置矩阵


表1 不同配置方案F 值Tab 1 Value of F in different configuration schemes
从表1 可以看出:Fa,Fb值最大,Fc值较小。这说明正交的配置方案,其导航特性较斜置配置方案的特性差。
3.2 可靠度比对
按照式(13),可计算图1(a)方案的可靠度为
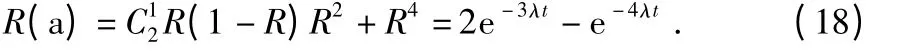
对应MTBF 为

由于图1(b),(c)方案任意3 个陀螺仪都不共面,则其构成的冗余系统正常工作的概率相等,可靠度为

对应MTBF 为

将式(18)~式(21)的计算结果列表如表2。

表2 单自由度陀螺仪系统的可靠度与MTBFTab 2 Reliability and MTBF of single degree of freedom gyros system
由表2 可以看出:4 个单自由度陀螺仪构成的冗余系统比无冗余系统可靠度高,说明利用敏感器件进行冗余是提高系统可度性的重要方法,图1(b),(c)所示方案的可靠度大于方案(a),即在陀螺仪数量相同的情况下,斜置方案优于正交方案。
4 对称斜置式冗余配置方案
基于前述分析可知,斜置式冗余方案在导航性能和可靠性方面均优于正交配置方案。因此,提出新的对称式斜置配置方案如下:
构建五面体使其侧面与底面夹角为54.73°,侧面为等边三角形,底面为正方形。选取底面中心为坐标原点,以底面对角线分别为x 轴、y 轴,z 轴与x 轴y 轴构成右手直角坐标系。将4 个陀螺仪测量轴分别垂直于五面体的4 个侧面,测量轴1 与x 负半轴、y 负半轴和z 正半轴夹角均为α,测量轴2 与x 正半轴、y 负半轴和z 正半轴夹角均为α,测量轴3 与x 正半轴、y 正半轴和z 正半轴夹角均为α,测量轴4 与x 负半轴、y 正半轴和z 正半轴夹角均为α,如图2所示。

图2 对称式四陀螺配置方案示意图Fig 2 Diagram of symmetrical configuration scheme of four gyros
根据配置方案,可列出其量测方程为

其中,md=[m1m2m3m4]T为测量值,ωd=[ωxωyωz]T为角速率待求值,Hd为配置矩阵。
当α=54.73°时,可计算得对称斜置式方案的配置矩阵

根据α=54.73°和五面体的侧面与底面的夹角也为54.73°可以推得:测量轴1 的方向相当于以x 负半轴、y 负半轴和z 正半轴方向的单位向量所构成的正方体的体对角线方向,其余测量轴方向类似推出。
根据式(10)可计算其F 值为

将Fd值与表1 的计算结果进行比较可知,Fd值最小。根据优化准则可知,对称式斜置方案是这4 个方案中最优的配置方案,易求

同时,由于对称式配置方案的任意三个陀螺仪均不共面,则其构成的冗余系统正常工作的概率相等,亦可按照式(20)、式(21)计算可靠度和平均无故障时间,计算结果与圆锥型配置相同。
图3 给出了四类配置方案随时间变化的可靠度曲线,其中,假设单个陀螺仪的MTBF 为5 000 h。
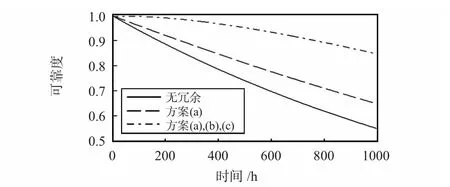
图3 冗余配置系统随时间变化的可靠度曲线Fig 3 Reliability curves of change with time redundancy configuration system
从图3 可以看出:冗余方案的可靠度始终高于非冗余方案,且在任意时刻方案(b),(c),(d)的可靠度始终最高。
通过上述的计算和分析可知,对称式配置方案是冗余数为4 时的最优配置方案,且优于圆锥型配置方案。
5 冗余配置方案精度分析
5.1 无故障情况
配置方案中的陀螺仪全部正常工作,根据公式(4)可知,系统的精度与配置矩阵H 和噪声方差σ2有关,噪声方差不可控制,因此,可以通过选择不同的配置矩阵来控制系统的估计精度。可以得到四种配置方案的M 值如表3 所示。

表3 不同配置方案M 值Tab 3 Value of M in different configuration schemes
其中,M=det(HTH),通过表3 可以看出:这4 个方案在陀螺仪全部正常工作时,测量精度相近。
5.2 单故障情况

选取工作模式124,则行列式的值为

同理,可求出配置方案(a),(b),(c),(d)其他工作模式的行列式值,计算结果如表4 所示。
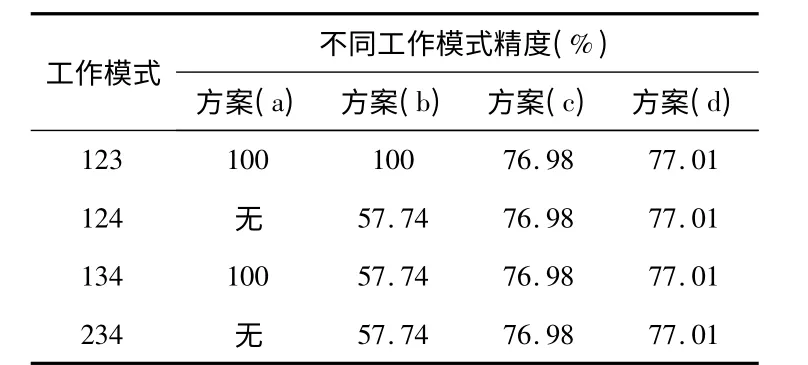
表4 单自由度陀螺仪工作模式精度计算Tab 4 Precision calculation of single degree of freedom gyros working mode
从表4 可以看出:方案(a)和方案(b)的123 工作模式的精度最高,它们均为正交配置,可见正交的配置方案比斜置的配置方案精度高。但方案(d)与方案(a)精度相差并不大,而且,方案(d)的各个工作模式的精度均相等,具有很好的一致性,这一点优于方案(a)和方案(b),方案(c)精度稍小于方案(d)的精度。因此,在优先考虑系统可靠性指标的前提下,综合考虑系统精度一致性,方案(d)是冗余数为4 时的最优配置方案之一。
6 结 论
针对四陀螺配置的冗余式捷联系统技术,以提高系统可靠性和导航性能为关键指标,在分析正交配置、斜置配置和圆锥配置的基础上,提出了对称斜置式四陀螺的冗余配置方案,并通过精度一致性、可靠性等分析验证了所提方案的有效性。这对于提高捷联式惯导系统的可靠性和精度,具有重要的实际意义。
[1] 尹逊和,林宝军,周 锐,等.伞形安装的陀螺系统性能分析[J].宇航学报,2008,29(1):178-182.
[2] 王京献,张明辉.一种高可靠捷联惯性测量单元布局[J].中国惯性技术学报,2012,20(3):363-367.
[3] 赵 剡,白雪峰.惯性导航系统冗余设计与可靠性分析[J].航空兵器,2006(1):15-17.
[4] 单 斌,缪 栋.捷联惯性测量组合的冗余设计和优化[J].导弹与航天运载技术,2004(3):25-30.
[5] 高豫强,祝君冬,赵 剡.捷联式惯导系统陀螺仪冗余配置研究[J].战术导弹技术,2008(2):62-66.
[6] 潘鸿飞,吕 隽,刘培毅.捷联惯导系统级余度技术研究[J].上海航天,2004(3):7-10.
[7] Yang C K,Shim D S.Best sensor configuration and accommodation rule based on navigation performance for INS with seven inertial sensors[J].Sensors,2009,9:8456-8472.
[8] 杨华波,张士峰,蔡 洪.空间冗余陀螺仪在轨标定方法[J].宇航学报,2010,31(1):104-110.
[9] Mahdi Jafari,Jafar Roshanian.Optimal redundant sensor configuration for accuracy and reliability increasing in space inertial navigation systems[J].The Journal of Navigation,2013,66:199-208.
[10]朱建丰,徐世杰.基于误差椭球理论的惯性部件构型分析[J].导弹与航天运载技术,2008(2):40-45.
[11]富 力,王新玲,岳亚洲.基于可靠性分析的最优冗余配置数量确定方法[J].北京航空航天大学学报,2010,36(9):1030-1033.
[12]Shim D S,Yang C K.Optimal configuration of redundant inertial sensors for navigation and FDI performance[J].Sensors,2010,1:6497-6512.
[13]吴光裕,武志忠,段成红.一种卫星用高可靠性的惯性敏感器[J].中国惯性技术学报,2004,12(1):70-73.
——对2018年广州市一道中考题的研究

