一种遗传神经网络潮位预测算法

罗 毅，阳 洋

(华北电力大学 控制与计算机工程学院，北京102206)

0 引言

潮汐是由海水受到地心引力、地球自转惯性离心力以及天体运动的引潮力而产生的潮水涨落现象。潮汐潮位预测对潮汐电站的日常运行是十分重要的，潮汐电站的日发电量与每日潮差大小密切相关，通过对潮水位的预测，可以预估潮汐电站日发电量、编制合适的发电计划［1］。根据预报的潮位，优化调度计算后，可以决定各时刻运行的库水位，并合理将电站总发电量流量分配至各台机组，达到潮汐电站的日发电量最大［2］。提高潮位预测的精度可为库水位调节、机组检修计划以及确定机组运行方式提供可靠依据，更好地制定运行调度计划，使潮汐能源得到充分的利用。

调和分析法是传统的潮位预测方法，将潮汐看作由许多振幅、周期及相位不同的分潮叠加而成，通过确定各分潮因子进行预报。其中，调和常数的确定常常需要大量的实测数据，不具有广泛实用性［3～6］。而另一方面，潮汐并不完全由周期性因素产生，还受海面风力、气压等气象因素以及海底地形变化等非周期性因素的影响，因此潮位变化具有非平稳性特点，这为潮位预测带来了困难。调和分析法无法对这些偶然气象因素或者某一海域的具体地形信息进行综合计算，影响了潮位预报精度。

近年来，智能化的预测方法受到了广泛关注，神经网络具有自学习能力、泛化能力、非线性映射能力强等优势而成为预报预测领域研究热点。Tsai 等［7］应用人工神经网络的方法，进行全日潮和半日潮的预测，与传统的调和分析法比较，人工神经网络的方法可以在有限数据基础上进行较高精度的短期、长期预测，但同时存在着收敛速度慢、训练时间长，预测与实际值之间的时滞问题。张巍等［8］根据潮汐形成的一般原理和规律，提出一种基于历史数据的Elman 神经网络预测模型，反映真实的潮汐趋势，这种方法能很好地解决训练时间、收敛速度的问题，但只能做几小时以内的短期预测，在实际应用中的优势并不明显。王先甲［9］提出了基于小波多分辨分析的BP 神经网络潮水位预测方法，将潮水位序列分解趋势项、周期项和随机项，利用BP 神经网络对每一项进行预测，但这种方法增大了计算量，且对预测精度提高优势并不明显。李明昌等［10］采用周期分析的概念，提出在预测前有针对性的数据处理分析方法，解决了潮位预测中存在的时滞问题，但对数据的预先处理会造成数据非线性关系的变形，影响潮位预测的精度。

由于传统神经网络的局限性，许多学者对神经网络算法进行了改进。粒子群算法和遗传算法是基于群体的优化工具，被广泛的用于函数优化，神经网络训练等多个领域［11～13］。卢辉斌［14］提出一种粒子群优化的RBF 神经网络模型，用粒子群算法来优化RBF 神经网络的权值，并用优化好的RBF 网络进行预测，但RBF 神经网络更多地针对负荷预测问题。肖迁［15］提出了遗传算法和神经网络的结合，通过优化神经初始网络权值的方法解决传统神经网络中收敛速度慢，易陷入局部最优等问题，但还没有见到应用于潮位预测的报道。

本文针对潮位变化具有非平稳性、周期性等特点，首先通过潮位数据的异常值检测，采用均值替换法克服由观测记录产生的数据误差;然后通过神经网络拓扑结构合理设计、节点优选、遗传算法优化初始网络权值与阈值等措施，建立了潮位预测模型，显著提高了潮位预测精度。

1 遗传神经网络预测算法

1.1 网络拓扑结构

BP 网络学习规则的指导思想是对网络权值和阈值的修正要沿表现函数下降最快的方向——负梯度方向。本文采用的神经网络的网络拓扑结构如图1 所示。

图1 网络拓扑结构

1.2 网络节点选择

图1 中，输入层节点数为ni，隐含层节点数为nh，输出层节点数为no。H1，H2，…，H8为前8 个整点时刻的潮位值，作为BP 网络的输入，网络输出即为预测的第9 个整点时刻潮位值。输入节点数对网络测试精度是有影响的，这直接反映了网络构建中拟合非线性函数的复杂程度。另一方面，输入节点数直接影响了神经网络中隐含层节点个数，而隐含层节点数增加会使非线性函数拟合更加精确，同时也大大增加了拟合非线性函数的复杂程度。图2 给出了输入层节点数对网络预测精度和训练时间的影响，表1 给出了不同输入节点数对隐含层节点数的影响，以及对神经网络测试精度的影响。隐含层的节点数可用下式来初步计算，然后用试凑法确定具体值:

图2 输入层节点数对网络预测能力的影响

表1 输入层节点数对网络预测能力的影响

采用均方根误差RMSE 对网络的预测能力做评价，其表达式为:

式中:Hi是潮位实际值;为预测值;m 为测试样本数。

采用相关系数(CC)评价预测的准确度，其表达式为:

式中:m 为测试样本数;Hi是潮位实际值;为预测值;为实际潮位平均值;为预测潮位平均值。

综合分析，节点取7，8，9 时能保证RMSE较低，但随着节点数增加，训练时间会明显增大，比较节点8 和节点9 时，RMSE 接近，但训练时间增幅较大，因此，选择输入节点数ni为8，隐含层节点数nh确定为15，即ni=8，nh=15，no=1。

输入样本从输入层，经过隐含层，产生输入-隐含层权值Wij，隐含-输出层权值Njt，i=1，2，…，8，j=1，2，…，15，t=1，沿着负梯度方向向输出层传播，减少预期与实际输出之间的误差，反方向从输出层向输入层传播修正各个连接权值。潮位预测的实质是根据其历史数据预测未来值，即认为第9 个整点潮位值与前8 个整点时刻潮位值存在某种非线性的函数关系:

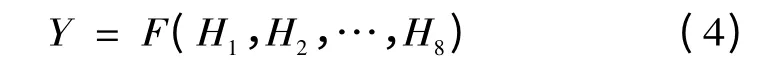
BP 神经网络预测即是利用BP 算法来拟合函数F(H)，然后将其应用于神经网络预测中。BP神经网络在开始训练前将各层的连接权值及阈值随机初始化为［0，1］之间的值，这种未经优化的随机初始化往往会使BP 神经网络的收敛速度慢且容易使最终结果为非最优解。因此，提出用遗传算法改进神经网络的初始权值和阈值，提高收敛速度和预测精度。

1.3 网络权值和阈值优化

遗传神经网络采用遗传算法优化神经网络的初始权值和阈值，种群的每个个体都包含一个网络所有权值和阈值，个体通过适应度函数计算个体适应度值，遗传算法根据选择、交叉、变异操作找到最优个体对网络初始权值和阈值赋值，经训练后预测输出。算法流程如图3。

图3 遗传神经网络算法流程

(1)种群初始化

个体编码方法是实数编码，每个个体都是一个实数串，由输入隐含层连接权值、隐含层阈值、隐含输出层连接权值以及输出层阈值4 个部分组成，个体包含神经网络全部权值和阈值。在本文中由于网络有8 个输入节点、1 个输出节点，设置网络结构为8-15-1，共有135 个权值，16 个阈值，故遗传算法个体编码长度为151。

(2)适应度函数

根据个体得到的初始权值和阈值，用训练数据训练BP 神经网络后预测数据输出，把预测输出与实际输出的绝对误差作为个体适应度值，网络输出只有1 个节点，适应度函数如下:

式中:yi为BP 神经网络中第i 个节点的期望输出;Oi是第i 个节点的预测输出;k 为系数。

(3)选择操作

遗传算法常用的选择操作有轮盘赌法、锦标赛法等多种方法，选择轮盘赌法，即基于适应度比例的选择策略。个体被选中的概率和适应度有关，个体适应度越好，表示预测与实际输出误差越小，选中的概率越大。

式中:Fi为个体i 的适应度值;k 为系数;N 为种群个体数目。

(4)交叉操作

交叉操作方法采用实数交叉法，第k 个染色体ak和第l 个染色体al在第j 位上的交叉操作方法如下:

式中:b 为［0 1］之间的随机数。

(5)变异操作

在种群中选择一个个体，选择染色体中的一点进行变异，以产生更优秀的个体。

式中:amax为基因aij的上界;amin为基因aij的下界;f(g)=r2(1- g/Gmax)2，r2为一个随机数，g 为当前迭代次数，Gmax是最大进化次数;r 为［0 1］间的随机数。

2 潮位预测应用

2.1 数据预处理

本文采用了福建莆田秀屿港3 个月的历史潮位数据，每小时记录一次，共计93 天的潮位数据，每8 h 作为输入向量，预测第9 h 的潮位做滚动预测，共计得到2 200 组数据，得到潮汐时间序列{Hk}，其中k=1，2，…，2 200。前2 000组数据做训练数据，用来对遗传神经网络构建最优权值和阈值。后200 组数据作为测试数据，对构建的网络进行精度测试。

所选取的港口潮汐具有潮差大，获得的观测数据由于观测条件的原因，与实际潮位有所偏差，每日记录数据中23 时和24 时的数据十分相近，这不利于遗传神经网络的预测。因此，将原始数据中每日23 时的数据用均值替换法集中处理:

式中:m表示数据记录天数，m=1，2，…，93。

将初步处理后的数据进行统一的归一化处理，作为遗传神经网络的输入:

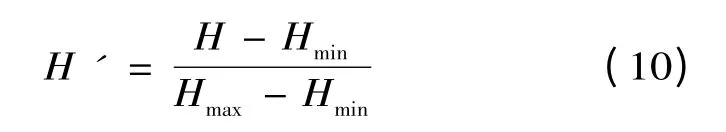
式中:H '表示归一化后的潮位值;H表示归一化前的潮位实测值;Hmax表示所有潮位数据中的最大值;Hmin表示所有潮位数据中的最小值。

图4表示每日潮位变化以及1 个月内潮位的变化。

图4 潮汐潮位周期性变化规律

每日潮汐潮位的变化具有周期性，所选取的秀屿港潮汐为标准半日潮，即一天之间为两次规则高低潮，在时间跨度上呈现近似三角函数的周期性变化［16］。

2.2 遗传神经网络预测潮位

构建的遗传神经网络，各个参数设置如下:迭代次数10 次，种群规模10，交叉概率取0．3，变异概率取0．1，学习速率0．01，隐含层15，训练方法为最快速下降法，方向为负梯度方向，适应度曲线如图5 所示。

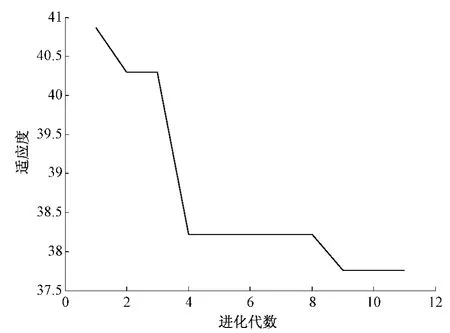
图5 适应度曲线

从中可以看出在第9 次迭代适应度下降达到要求，并维持稳定值，说明了遗传算法的有效性。图6(a)为采用遗传神经网络预测的结果，结果表明，经过遗传算法优化的神经网络能较好的预测潮位。图6(b)为预测值与实际值的误差，误差集中在［- 20，20］之间，结合潮位值在［100，800］之间变化，相对误差较小，满足精度要求。图6(c)为200 h 内实际潮位与预测潮位之间的比较，其中相关系数CC 为0．999 1。

2.3 算法比较分析

为了验证本文提出的遗传神经网络算法的效果，本文采用传统神经网络(BP)、粒子群算法优化神经网络(PSO-BP)、遗传算法优化神经网络(GA-BP)等3 种方法来预测潮位，比较潮位预测精度。

图7(a)为采用传统BP 神经网络算法预测潮位结果，从图中明显看出在潮位潮高的预测上误差较大，并且有时滞现象。这主要是由于BP 算法依赖于初始权值的选择，收敛速度缓慢且容易陷入局部最优，上述缺陷尤其是局部优化特性使其训练的神经网络的输出具有不一致性和不可预测性。图7(b)为比较实际潮位与预测潮位，可以看出相关性并不理想，CC 为0．990 0。

图6 GA-BP 预测结果

图8(a)为采用PSO 神经网络预测潮位的结果，从图中可以明显看出在潮高上的预测并不理想，这是因为PSO 算法本身是一种寻优算法，在潮位预测上的优势并不明显，这也说明了PSO 并不适用于潮位预测。图8(b)中采用PSO 算法的网络预测值与实际值的相关系数为CC 为0．995 0。

表2 中列出了3 种算法正负最大误差和均方根误差。可以看出，PSO-BP 并未减小误差，这主要是因为PSO-BP 本身是一种随机搜索算法，并不能保证搜索到全局最优，因此会出现误差较大的情况，不太适合潮位预测。显然，GA-BP 算法预测精度明显高于其余两种方法。

图7 BP 网络预测结果

表2 算法比较

3 结论

本文在潮位数据的异常值检测进行均值替换处理的基础上，通过优选神经网络节点数、遗传算法优化初始权值和阈值，构建了遗传神经网络预测模型，用实际港口的数据信息进行潮位时间序列的预测，对比分析BP 网络、GA-BP 网络、PSO-BP 网络3 种不同算法，发现GA-BP 显著提高了潮位预测精度，取得了良好的应用效果，表明了GA-BP 在潮位预测上的有效性，为潮汐电站的优化运行与调度提供了依据和有效途径。

图8 PSO 网络预测结果

［1］甘泽，李志刚．潮汐发电中调和分析与人工神经网络预测潮位［J］．河北联合大学学报(自然科学版)，2014，36(1):84-87．

［2］赵帅帅，陈成军，洪军，等．偏心叶片式潮汐能发电装置的设计及其仿真［J］．科学技术与工程，2014，14(8):131-135．

［3］裴文斌，牛桂芝，董海军．余水位及潮汐差分方法［J］．水道港口，2007，28(6):439-443．

［4］李大鸣，欧阳锡钰，潘番，等．考虑波浪辐射应力的潮流泥沙数学模型［J］．海洋通报，2014(6):703-711．

［5］张沈阳，何文亮．马迹山港区潮汐、潮流现势分析［J］．浙江水利科技，2013，41(5):23-24，30．

［6］刘曾美，覃光华，陈子燊，等．感潮河段水位与上游洪水和河口潮位的关联性研究［J］．水利学报，2013，(11):1278-1285．

［7］Tsai C P，Lee T．Back-propagation neural networks in tide forecasting［J］．Journal Waterway，Port，Coastal and Ocean Enginering，1999，125(4):195-202．

［8］张巍，沈寿林，白承森．一种神经网络的偏远海区潮汐仿真预测［J］．计算机仿真．2011，28(4):172-175．

［9］王先甲，李匡．基于小波分析的BP 神经网络潮水位预测方法．［J］．水电能源科学，2006，24(2):66-69．

［10］李明昌，梁书秀，孙昭晨．人工神经网络在潮汐预测中的应用研究［J］．大连理工大学学报，2007，47(1):101-105．

［11］唐贤伦，李洋，李鹏，等．基于多Agent 粒子群优化的多步SVR 模型预测控制［J］．系统工程与电子技术，2014，36(5):958-964．

［12］姜鸿羽，马宏忠，梁欢，等．改进粒子BP 神经网络在变电站噪声控制中的应用［J］．中国电力．2014，47(9):71-76．

［13］程诚，祝一欣，王静雅．人工神经网络在青草沙水库库外潮位预测中的应用研究［J］．科协论坛(下半月)，2013，(12):51-52．

［14］卢辉斌，李丹丹，孙海艳．PSO 优化BP 神经网络的混沌时间序列预测［J］．计算机工程与应用，2015，51(2):224-229．

［15］肖迁，李文华，李志刚，等．基于改进的小波-BP 神经网络的风速和风电功率预测［J］．电力系统保护与控制，2014，42(15):80-86．

［16］庄祖垠，姜华，易淑昌，等．基于潮位预测的潮汐校正技术的应用［J］．工程地球物理学报，2013，10(3):286-290．