一种约束稳定性最小均方噪声对消算法*

张炳婷，赵建平，陈 丽,盛艳梅

(曲阜师范大学 物理工程学院,山东 曲阜 273165)

一种约束稳定性最小均方噪声对消算法*

张炳婷，赵建平，陈 丽,盛艳梅

(曲阜师范大学 物理工程学院,山东 曲阜 273165)

研究了最小均方误差(LMS)算法、归一化的最小均方(NLMS)算法及变步长NLMS算法在自适应噪声干扰抵消器中的应用，针对目前这些算法在噪声对消器应用中的缺点，将约束稳定性最小均方(CS-LMS)算法应用到噪声处理中，并进一步结合变步长的思想提出来一种新的变步长CS-LMS算法。通过MATLAB进行仿真分析，结果证实提出的算法与其他算法相比，能很好地滤除掉噪声从而得到期望信号，明显的降低了稳态误差，并拥有好的收敛速度。

约束稳定性；变步长；噪声抵消；稳态误差

0 引 言

目前自适应噪声对消器的用途十分广泛，常被用于语音通信的噪声抵消，天线旁瓣干扰消除和生物医学信号检测中的干扰抵消等领域[1]。自适应噪声抵消器的核心是自适应滤波器，通过自适应算法来实现对参数的控制，从而实现最佳滤波。在具体的自适应噪声抵消系统中，信号的输入增加了相关的噪声信号作为参考输入信号，从而获得更多的噪声信息，达到好的降噪效果，能够从被噪声干扰的环境中获得有用信号[2]。针对不同的自适应算法在自适应噪声对消应用中存在的不足之处，本文将一种新的算法约束稳定性最小均方(Constraint Stability LMS,CS-LMS)算法[3]应用到自适应噪声对消的系统当中，进行仿真比较分析。最后结合变步长的思想提出变步长的CS-LMS算法，进行进一步的仿真研究。

1 自适应噪声对消系统的原理

自适应噪声对消器是一个具有两端输入的自适应滤波器，主要分析采用LMS算法的噪声对消器，它的原理图如图1所示：原始信号d(n)从信号源发出的有用信号s(n)与从噪声源产生的噪声g(n)干扰叠加得到的，而参考输入信号x(n)是一个与有用信号s(n)无关，与噪声信号g(n)相关的信号即是噪声源产生的信号h(n)。经过分析，同源噪声在某种程度上是相关的，而噪声和有用信号间是相互独立的这个前提下，经过多次自适应滤波器的迭代，使滤波器的输出y(n)无限接近噪声干扰信号g(n)，这样系统的输出信号e(n)就近似等于我们需要的有用信号s(n)[4]。系统的均方误差即输出信号的均方值：

E[e(n)2]=E[d(n)-y(n)2]=E{[s(n)+g(n)-y(n)]2}=E[s(n)2]+E{[g(n)-y(n)]2}+2E{s(n)[g(n)-y(n)]}

(1)

因为s(n)与g(n)和h(n)是不相关的，则式(1)可写为E[e(n)2]=E[s(n)2]+E{[g(n)-y(n)]2}，又信号的输入功率和自适应调节无关，所以要让E[e(n)2]最小即使E{[g(n)-y(n)]2}最小，也就是系统的输出信号e(n)与有用信号s(n)的均方差最小。在自适应对消系统中，自适应滤波器在的调节下改变自身的权系数，使得系统的输出误差均值E[e(n)2]最小，从而达到干扰对消的目的[5]。

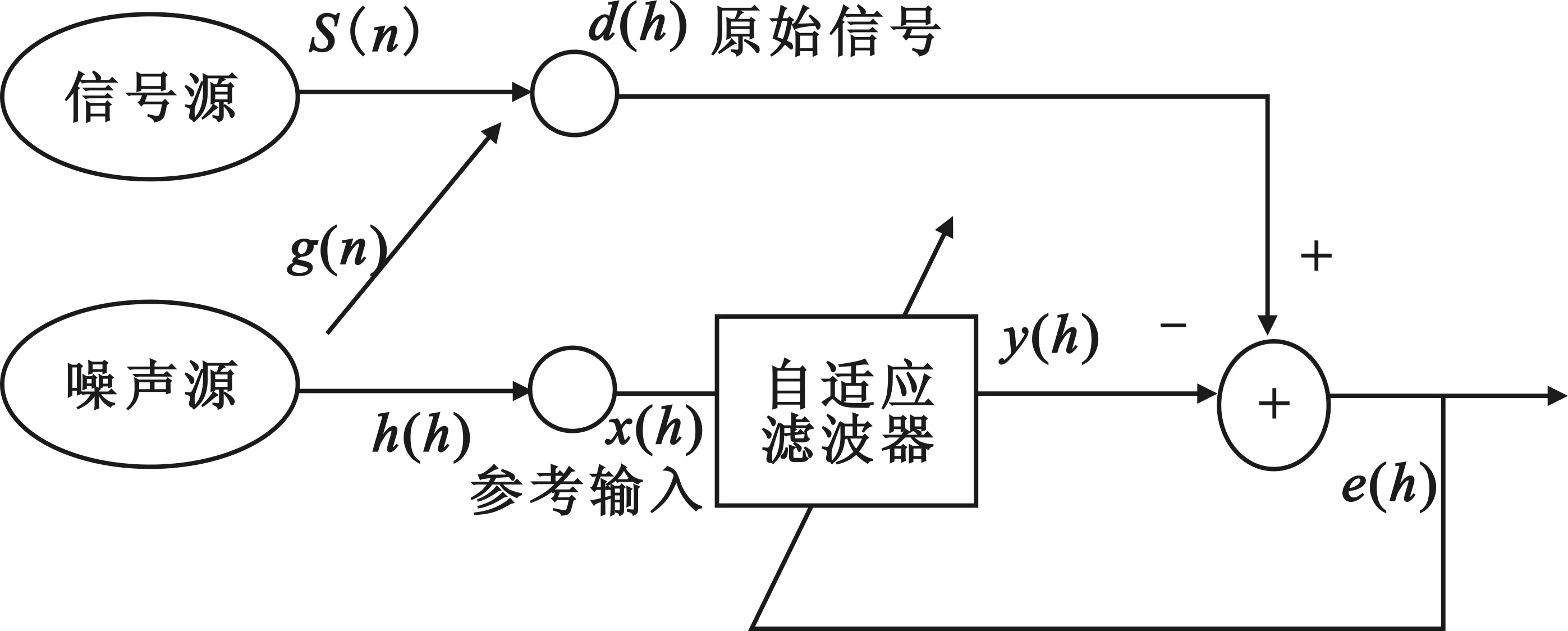
图1 自适应噪声对消系统框

2 算法的分析

2.1 传统的LMS算法

最小均方误差(LMS)算法，它是以期望响应和滤波器输出信号之间误差的均方最小值为准则，并使用误差来控制自适应滤波器的权系数，是最终输出的权系数达到最佳的权系数。针对自适应噪声对消系统，LMS算法的表达式：

y(n)=w(n)Tx(n)

(2)

d(n)=s(n)+g(n)

(3)

e(n)=d(n)-y(n)

(4)

w(n+1)=w(n)+ue(n)x(n)

(5)

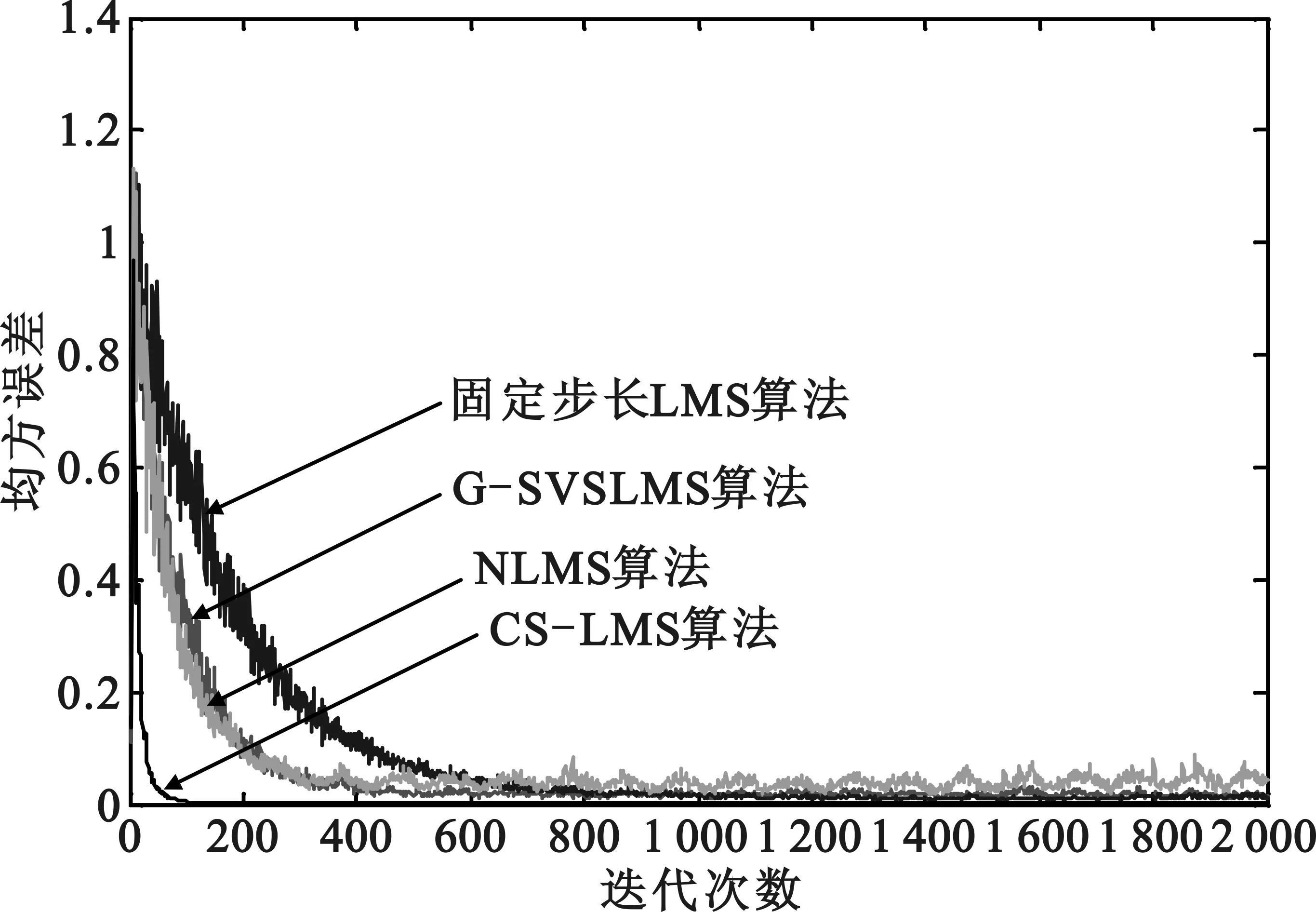
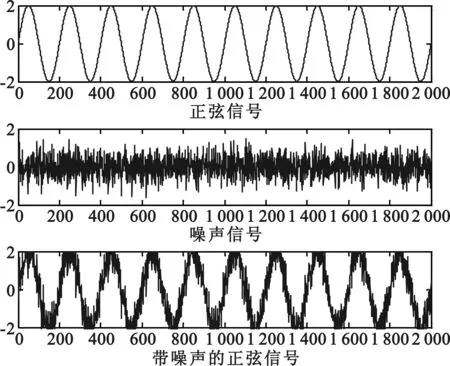
式中，x(n)是参考输入信号,d(n)是输入端的原始信号,y(n)是自适应滤波器输出的信号,w(n)是滤波器的抽头系数。则误差信号e(n)是有用信号s(n)的最佳估计。式(5)是自适应滤波器抽头权向量的递推公式，u是步长因子，当满足0

w(n+1)=w(n)+u(n)e(n)x(n)

(6)

式(6)中u(n)=β(1-exp(-α|e(n)|2))，β控制步长函数的取值范围，α控制步长函数的形状。该算法具有较小的稳态误差和较快的收敛速度。但是在外界噪声严重的情况下，稳态误差较大。

2.2 NLMS算法

对于基本的LMS算法，它的收敛速度和稳态误差和自适应滤波器权系数矢量的系数目和输入信号的输入功率有关，当输入信号功率增大时，会带来大的稳态误差，对梯度噪声敏感，这一问题在噪声抵消系统中尤为关键。为了解决这一问题，对基本的LMS的步长因子进行了归一化[7]的处理，从而降低了算法对梯度噪声的敏感度，减小了稳态误差，提高了收敛速度。

具体来说NLMS算法的步长因子表达式：

(7)

权向量更新表达式：

(8)

其中uo是固定步长因子，当满足0

该算法的步长表达式：

保护装置中非选择性动作概率是指当电气设备发生故障时跳闸的越级动作。越级跳闸的原因有很多种如环境，温度，电子元件参数的不稳定等。因而在设计电力保护系统设备时要充分考虑这些因素。对于可能发生的越级跳闸，要采用必要的方案对策。仔细研究对于因环境，温度变化或者元器件的损害导致的越级跳闸动作发生的概率，计算因这些因素导致的发生越级跳闸非选择性动作概率。

u(n)=β[1-exp(-α|e(n)e(n-1)|)]

(9)

权向量的更新表达式：

(10)

就是在步长函数中不直接使用误差信号e(n)的平方，而是使用前一时刻的误差信号e(n-1)与当前时刻的误差信号e(n)的乘积即e(n-1)e(n)来代替，降低了算法对噪声的敏感度。同时采用变步长算法。达到在收敛阶段，采用大的步长，加快收敛速度，等到收敛稳定后，采用小的步长，来降低稳态误差的目的。

2.3 CS-LMS算法

与NLMS算法不同CS-LMS算法在运算的过程中放松了对NLMS算法的约束条件，使用拉格朗日乘子法求解最佳优化问题，得到约束稳定性最小均方CS-LMS算法的权值更新方程。它的权向量更新表达式为：

(11)

式(11)中δe(n)=e(n)-e(n-1)，是相邻的误差增量，‖δx(n)‖2=‖x(n)-x(n-1)‖2是参考输入信号增量的范数的平方，当‖δx(n)‖2≠0算法收敛。由于NLMS算法优化问题的约束条件是让后验误差为零，过于苛刻，会使算法在稳态时收敛过度，会产生较大的稳态误差，而CS-LMS算法放松约束条件后使后验误差趋于一定值，这样改善了NLMS算法稳态误差偏大的现状[9]。

2.4 改进的变步长CS-LMS算法

CS-LMS算法的步长仍是固定的，本文在CS-LMS算法的基础上结合变步长的思想提出了变步长的CS-LMS算法。这样可以达到在收敛阶段，采用大的步长，加快收敛速度，等到收敛稳定后，采用小的步长，来降低稳态误差的目的。将文献[10]中提出变步长算法与CS-LMS算法结合得到的变步长CS-LMS算法的步长表达式如下：

u(n)=αu(n-1)+β|e(n)e(n-1)|

(12)

权向量更新表达式：

(13)

该算法采用变步长的思想，解决了稳态误差和收敛速度间的矛盾，同时又放松了约束条件，进一步的减小了稳态误差，归一化的处理让算法降低了对梯度噪声的敏感度。

3 仿真结果及性能对比分析

3.1 算法对输入信号敏感程度的分析

将不同的算法应用到噪声抵消系统中，验证不同算法在不同大小的输入信号下滤除噪声的性能，主要从稳态误差和收敛速度两个方面来进行对比。针对不同算法选取相同的输入正弦信号s(n)=2*sin(0.01*pi*n)，噪声信号noise=randn(1,n)，其中滤波器的阶数是4，为保证算法的收敛，步长选取适当的值。对于固定步长LMS算法，取步长为u=0.003，G-SVSLMS算法中选取β=0.006,α=0.8，NLMS算法中uo=0.04,γ=1，CS-LMS算法中uo=0.3,γ=1，分别做200次独立仿真，采样点数为2 000，以瞬时误差作为均方误差的简单估计，求它们的统计平均，得到算法的学习曲线图如图2所示。由图2可以看出，CS-LMS算法的收敛速度和稳态误差确实都要优于其他的算法。

图2 不同算法的学习曲线

将噪声信号改为noise=0.5*randn(1,n)，即改变输入信号的功率时再用相同的4种算法进行仿真分析，得到的学习曲线如图3所示。对比图2与图3可以清楚地看到NLMS算法和CS-LMS算法的收敛速度不受输入信号功率变化的影响，克服了对输入噪声较为敏感的缺点。而另外两种算法对输入信号功率变化十分敏感。综上CS-LMS算法的收敛速度和稳态误差都要优于其他算法，而且不易受输入信号功率变化的影响。

图3 不同算法的学习曲线

3.2 不同算法噪声对消结果的分析

将CS-LMS算法、VSSNLMS算法和变步长的CS-LMS算法应用到具体的自适应噪声对消系统中，定义滤波器的输入正弦信号为s(n)=2*sin(0.01*pi*n)，噪声信号为noise=0.5*randn(1,n)，其中滤波器的阶数是4，为保证算法的收敛，步长选取适当的值。将变步长CS-LMS算法中α=0.7,β=0.09，VSSNLMS算法中α=0.8,β=0.04，CS-LMS算法的uo=0.2,γ=1每种算法独立做200次仿真，然后对其求平均值。

图4是有用的正弦信号、噪声信号和加入噪声信号后的正弦信号，图5是不同的LMS算法自适应对消后的结果，与图4中的正弦信号相比，明显看出CS-LMS算法和本文提出的变步长CS-LMS算法滤除噪声恢复信号的效果要好。图6是变步长VSSNLMS算法、CS-LMS算法、变步长CS-LMS算法的学习曲线图，显然CS-LMS算法、变步长CS-LMS算法的稳态误差低于变步长VSSNLMS，收敛速度也要快许多，这其中本文提出的变步长CS-LMS的性能最好。

图4 信号的波形

图5 不同LMS算法的噪声对消后的结果

图6 不同算法的学习曲线

4 结 语

文中对目前自适应噪声对消器的应用和原理做了简单的说明，研究了传统的LMS算法、NLMS算法及变步长算法的对消过程，针对它们的不足之处，将CS-LMS算法应用到自适应噪声对消系统中，并结合变步长的思想，提出了一种新的变步长CS-LMS算法，最后对文中提到的算法进行了仿真，仿真结果证明，在自适应噪声对消的应用中，本文提出的算法降低了对梯度噪声的敏感度，同时不仅加快了算法的收敛速度，也大幅度的减小稳态误差。但是稳态误差的收敛过程起伏较大，在接下来的研究当中，会对本文的算法进一步的改进，并在硬件当中进行实施。

[1] Widrow B,Mccool J M, Arimoer M G. Stationary and No Stationary Learning Characteristic of the LMS Adaptive Filter[J],Proc IEEE,1976,64(8):1151-1162.

[2] 褚嵘.基于DSP的自适应噪声抵消器设计[D].武汉:武汉理工大学，2005. CHU Rong.Design of Adaptive Filter based on DSP System [D].Wuhan: Wuhan University of Technology,2005.

[3] Amjad Khan G,Dr. Sreenivasa Murthy K E.Noise Cancellation in Speech Signals by Using a Constrained Stability LMS Algorithm. International Journal of Engineering Research and Applications (IJERA) Vol. 2, Issue 1, Jan-Feb.

[4] 任晓亚，宋爱民.自适应算法在干扰抵消器应用中的比较研究[J].通信技术，2007,40(12):48-50. REN Xiao-ya, SONG Ai-min. Comparison of Adaptive Filtering Algorithm Used in Interference Cancellation System[J].Communications Technology,2007,40(12),48-50.

[5] 曹斌芳.自适应噪声抵消技术的研究[D].长沙:湖南大学, 2007. CAO Bin-fang .Research on Adaptive Noise Cancelling Technology [D].Changsha: Hunan University,2007.

[6] 高鹰,谢胜利．一种变步长LMS自适应滤波算法及分析[J].电子学报，2001,29(08)：1094-1097． GAO Ying, XIE Sheng-li. A Variable Step Size LMS Adaptive Filtering Algorithm and Its Analysis [J].Act Electronic Sinica,2001,29(08)：1094-1097．

[7] 张琦,王霞等.自适应回波抵消中变步长NLMS算法[J].数据采集与处理,2013,29(01):35 - 41. ZHANG Qi,WANG Xia, et al. Variable Step Size NLMS Algorithms in Echo Cancellation [J].Journal of Data Acquisition and Processing,2013,29(01):35-41.

[8] 宋杰，龙腾，何友.一种新的直达波干扰变步长NLMS算法[J].北京理工大学学报,2015,35(01):105-110. SONG Jie, LONG Teng,HE You. An Adaptive Cancellation of Direct Wave Interference Using a New Variable-Step-Size NLMS Algorithm [J]. Translation of Beijing Institute of Technology, 2015，35(01)：105-110.

[9] 张会芝，杨育捷，王鲜芳 .一种约束稳定性最小均方波束形成算法[J].电光与控制,2014,3(21):33-37. ZHANG Hui-zhi, YANG Yu-jie, WANG Xian-fang. A Constrained Stability Least Mean Square Beam Forming Algorithm[J].Electronic Optics & Control,2014,3(21),33-37.

[10] 强建龙，蔡灿辉.一种改进的低复杂度变步长LMS算法[J].通信技术，2014,47(03):258-261. QIANG Jian-long, CAI Can-hui. An Improved Low Computational Complexity Variable Step-Size LMS Algorithm [J]. Communications Technology,2014,47(3),258-261.

A Constrained Stability Least Mean Square Noise Cancellation Algorithm

ZHANG Bing-ting，ZHAO Jian-ping，CHEN Li，SHENG Yan-mei

(College of Physics Engineering ，Qufu Normal University ， Qufu Shandong 273165，China )

The least mean square error (LMS) algorithm, normalized least mean square (NLMS) algorithm and variable step NLMS algorithm in adaptive noise canceller are studied, and aiming at the shortcomings of these algorithms in applications, the constrained stability least mean square (CS-LMS) algorithm is applied to dealing with noise,and further combined with the thought of variable step size,a new variable step size CS-LMS algorithm is proposed. Simulation with MATLAB indicates that this proposed algorithm, as compared with other algorithms, could fairly filter out the noise so as to acquire the desired signal, significantly reduce the steady-state error, and has excellent convergence speed.

constraint stability; variable step size; noise cancellation; steady-state error

2015-03-25；

2015-07-19 Received date:2015-03-25；Revised date：2015-07-19

国家自然科学基金(No.11302118)；山东省自然科学基金资助(No.ZR2014FM011)

Foundation Item:National Natural Science Foundation of China(No.11302118)，Natural Science Foundation of Shandong Province (No.ZR2014FM011)

TN929.5

A

1002-0802(2015)09-1010-05

张炳婷(1990—)，女，硕士研究生，主要研究方向为无线通信技术；

赵建平(1964—)，男，教授，主要研究方向为无线通信技术；

陈 丽(1990—)，女，硕士研究生，主要研究方向为光纤通信技术；

盛艳梅(1991—)，女，硕士研究生，主要研究方向为智能信息处理。

10.3969/j.issn.1002-0802.2015.09.006