SVD降噪在载波同步技术中的研究*

杨晗竹, 李广侠,赵陆文, 张敬义

(解放军理工大学 通信工程学院,江苏 南京 210007)

SVD降噪在载波同步技术中的研究*

杨晗竹, 李广侠,赵陆文, 张敬义

(解放军理工大学 通信工程学院,江苏 南京 210007)

为了提升突发通信中载波频偏估计的性能，降低有效估计的信噪比门限，提出了一种基于奇异值分解去噪的频偏估计方法。首先，该方法将含噪信号根据相应映射转换成矩阵，并对该矩阵进行奇异值分解；其次，将较大的奇异值判定为信号特征予以保留，否则判定为噪声特征置零；接着，根据降噪后的奇异值重构矩阵，恢复成模拟信号；最后，将预处理后的信号进行M&M频偏估计。结果表明，相比于不去噪的频偏估计算法，该方法能够提升估计精度，降低信噪比门限，具有一定的实用性。

突发通信；频偏估计；奇异值分解

0 引 言

载波同步技术是通信过程中需要解决的一个关键问题。在通信系统中，数据序列经过载波调制后，由射频系统通过信道发射出去，接收机接收到的数据参数会受到信道、接收机和发送机的影响。为了使判决装置能够准确恢复出发送数据，接收机必须要能够准确估计出信号参数。同步技术在本质上就是对信号参数进行准确估计和矫正。

在无线数字通信系统中，多普勒效应、码间串扰、多径衰落、系统噪声等问题的存在，造成了信号的损耗，对载波同步产生很大阻碍。在这些损耗中，影响接收机性能的一个重要原因是频率偏移。时间离散信道脉冲响应受到频偏的影响发生旋转，使得接收机中的自适应信道估计器无法对信道的变化进行有效的跟踪。当外界干扰严重甚至达到一定程度时，频偏将会影响到解调的性能。因此，为了实现载波同步，对频偏进行估计与补偿是非常重要的。

目前为止，国内外已经对频偏估计提出了不少方法，主要分为时域，频域及时-频分析算法等。

频域类算法方面，频偏估计值利用的是信号FFT后获得的谱线，适应的频率动态范围最好能达到一半的采样频率。由于FFT普遍存在栅栏现象，直接获得精确的频偏估计值在实际应用中难以实现。Rife算法根据信号FFT后幅度最大的两根谱线，经插值获得关于频率的精确估计[1]。Quinn算法同样利用幅度最大的两根FFT谱线，但其插值利用的是谱线的复数值之比的实部，其估计性能随着频率波动的情况要好于Rife算法，但依然存在严重恶化[2]。

时域类算法方面，Kay算法易于实现，可是其工作门限很高，在低信噪比条件不能适用[3]。Fitz算法具有较低的信噪比门限，但具有以下3个缺点：适应的频率范围有限；运算量随观察区间长度的增加迅速增长；只能估计频率，相位估计还需额外的算法[4]。L&R算法的精度在之前的算法上有了一定提升，并且运算量小，硬件实现较为简单，但是频偏估计范围较窄，其适用范围比较偏向收发双方动态性较低的情况[5]。M&M算法因为在原理上做出了一些创新，相比于其他算法扩大了频偏估计的范围，并且其方差在有效范围内已经非常接近于克拉美罗界，只是M&M算法的信噪比门限较高，不适用于低信噪比的情况[6]。

近些年，有很多研究者在经典算法的基础上研究出了一些优化算法，在性能上有所提升[7-12]。

针对M&M算法实现简单，方差接近理论极限，且估计范围相对较大的优势，在其基础上进行优化创新，通过将信号进行奇异值分解降噪预处理，从而改变M&M算法工作门限较高的缺点，增强其在复杂的低信噪比现实环境中的实用性，达到性能的提升。将新算法简称为SVD-MM算法。

1 奇异值分解去噪

奇异值分解(Singular Value Decomposition, SVD)同特征值分解目的一样，都是将复杂的矩阵分解为简单的子矩阵，且子矩阵能够表征复杂矩阵的重要特征。

1.1 特征值分解

矩阵A的特征值分解可表示成：

A=QΣQ-1

(1)

式中，矩阵Σ为对角阵，且仅对角线上存在由大到小排列的特征值，其他非对角线上值为0。对角线上的特征值越大，越能表征矩阵A的特征。矩阵Q是由矩阵A中每个特征值对应的特征向量所组成的矩阵。

1.2 奇异值分解

对于较复杂的矩阵，特征值分解能够简化且较准确提取矩阵的特征值，但特征值分解的前提是矩阵必须是方阵，而在现实的通信环境中，信号矩阵常常不是方阵，奇异值分解是一种能适用于任意矩阵的分解方法：

A=UΣVT

(2)

式中，A是m×n维的矩阵，经过奇异值分解后得到的矩阵U称为左奇异向量，是m×m维的方阵，且矩阵U中的行向量正交；Σ是m×n维的矩阵，仅对角线上存在奇异值σ，其它的元素均为零；VT称为右奇异向量，是n×n维矩阵，矩阵中的向量正交。

1.3 基于奇异值分解的信号降噪

与特征值分解方法类似，信号矩阵经过奇异值分解后，如式(2)所示，矩阵Σ中的奇异值σ按照由大到小顺序排列，σ越大越能表征信号矩阵的特征，且在σ值下降速率较快时，采用前10%甚至1%的奇异值就能较好地表征信号矩阵的特征。基于这个特性，考虑采用前r项的奇异值来近似描述矩阵的特征[13]：

(3)

在式(3)中，r越接近n，近似描述效果越接近原信号矩阵A。

在现实的通信过程中，通信信号中常混杂有噪声信号，将该混合信号按照一定排列组合生成矩阵，经过奇异值分解得到从大到小的奇异值σ。当信噪比在一定门限范围内时，通信信号的特征较为明显，奇异值的前几项较大；高斯白噪声的特征数量较多但不明显，呈现杂乱的规律，奇异值对应后面多且小的部分。SVD去噪的过程，就是从m×n维矩阵中提取出r×r维矩阵的过程，当Σr×r越能代表通信信号的特征，最终得到的重构信号去噪效果就越明显(见图1)。

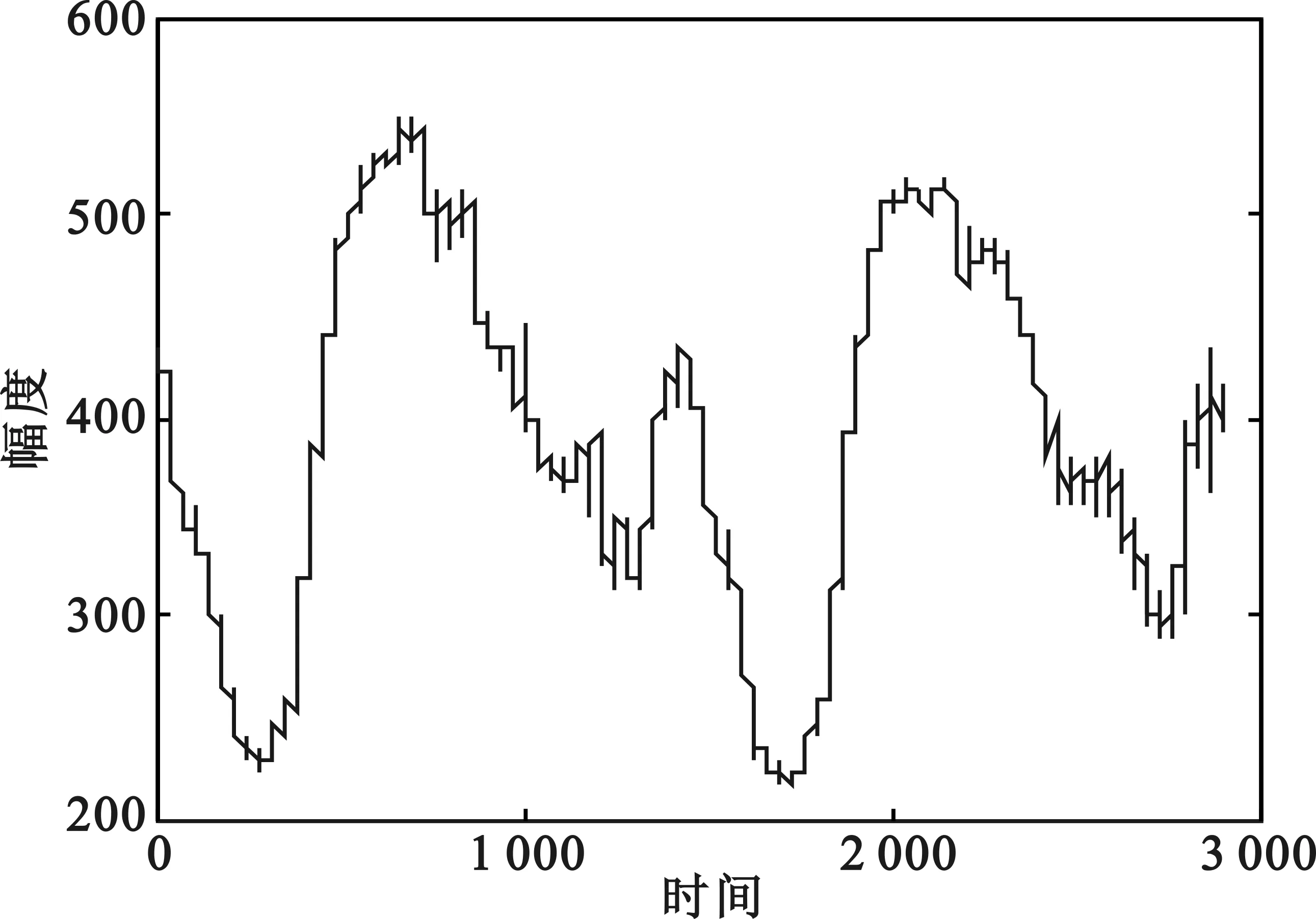
(a)原始信号

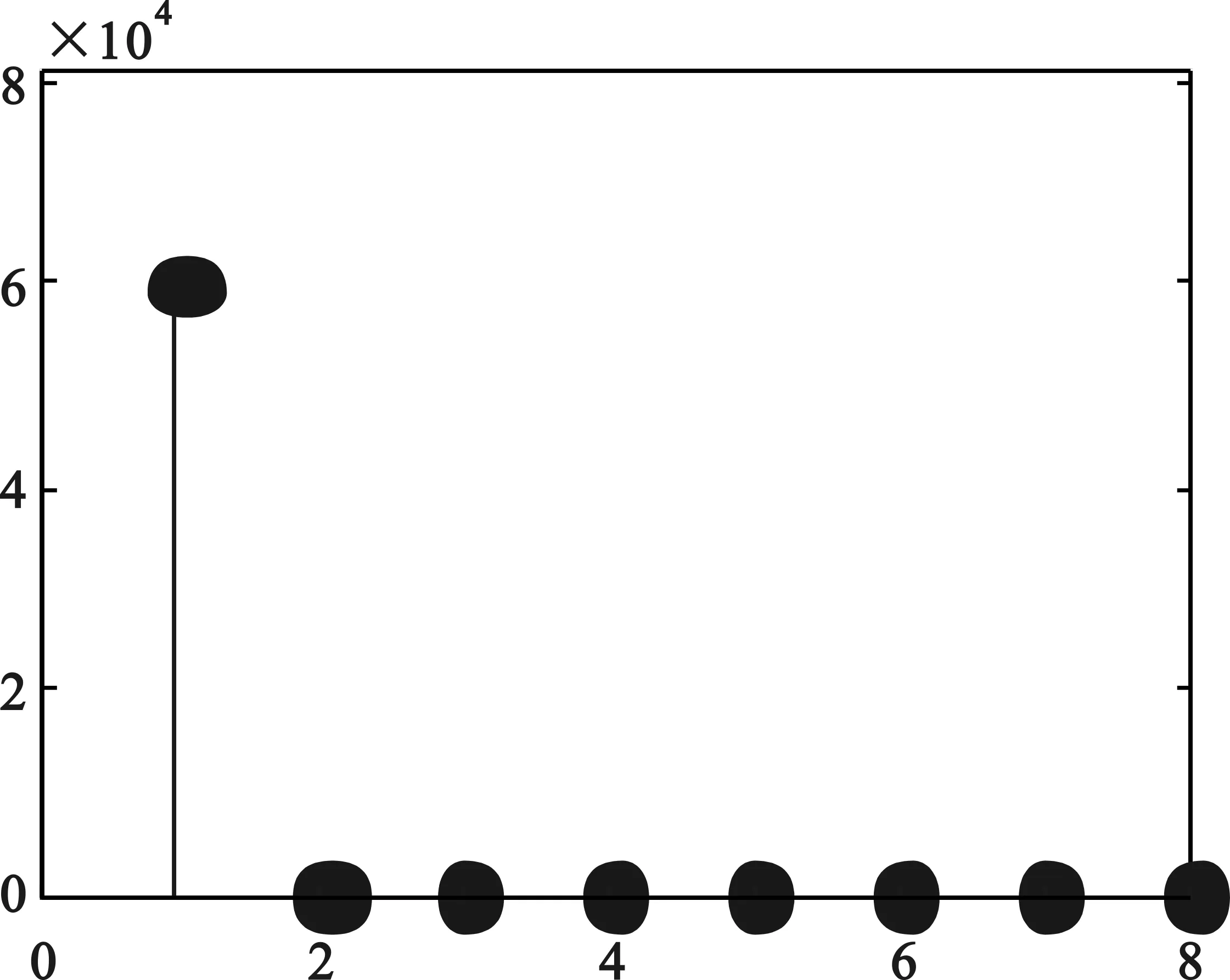
(b)特征值

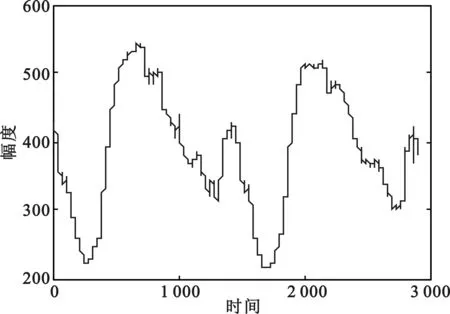
(c)滤波之后的信号：阈值为平均值

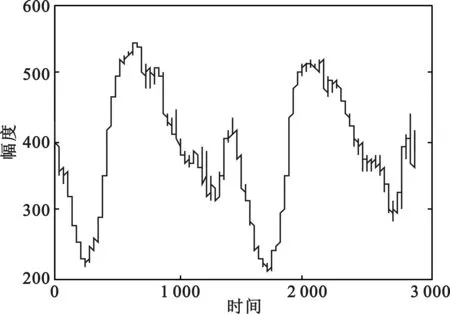
(d)滤波之后的信号：阈值为中值

从图1容易看出，奇异值分解法去噪效果较明显。奇异值分解后得到的前8个特征值中，主特征值大约为60 000，远大于其它特征值，说明信号特征较噪声更加明显。有效特征值范围的选取对去噪效果有着很大影响。图1(c)、图1(d)选取的特征值阀值分别为平均值和中值，在重构过程中，将大于阀值的特征值看作是有效信号的特征值，保留并带入计算；小于阀值的特征值看作是噪声的特征值，置为零。从仿真图1中可以看出，以均值作为阀值去噪的效果更加明显。

阀值的选取有很多种，可以有平均值，中值，或者最大值；甚至在知道原信号主频个数时，有效特征值个数可以选取为主频个数的两倍[14]，这样能够保证重构信号最接近有效信号，即去噪效果最好。

2 M&M频偏估计算法

Umberto Mengali和M.Morelli于1997年提出了M&M算法[6]。对信号求自相关函数后，该算法对自相关函数的相位差分结果进行平滑，将平滑结果作为载波的频率估计值。

首先对信号求自相关函数，对自相关函数采样得到自相关序列后，再分别进行不同的运算。

定义arg[R(m)]的自相关函数为：

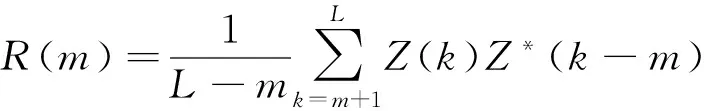
1≤m≤L-1

(4)

式(4)另一种表达方式为：

R(m)=ej2πmfT+n(m)

(5)

式中，n(m)为零均值的噪声项。从式(5)可以看出，自相关函数R(m)提供了用于频率估计的全部信息，是基于自相关函数的频率估计方法的基本依据。

式(5)还可表述为如下形式：

R(m)=ej2πmfT[1+γ(m)],1≤m≤N

(6)

式中，N为不大于L/2的参数。γ(m)=

(7)

由式(6)可以计算得到相位：

arg[R(m)]=[2πmfT+γ1(m)]2π,1≤m≤N

(8)

式中，γ1(m)为γ(m)的虚部。为了求取f的值，必须将非线性式展开为线性关系式，但是这种操作在低信噪比的条件下是很难实现的，本文提出在f与相位增量φ(m)=[arg[R(m)]-arg[R(m-1)]]2π之间建立联系，避免了f和arg[R(m)之间直接建立的非线性关系。

将式(7)带入φ(m)，得到φ(m)可以表示为：

φ(m)=2πfT+γ1(m)-γ1(m-1),2≤m≤N

(9)

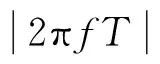
(10)

式中，ω(m)为平滑函数，表达式为：

(11)

3 基于SVD降噪的M&M频偏估计

3.1 SVD-MM算法描述

由于信号的奇异值反映了接收信号中有用信号和噪声的能量分布情况，故可以通过对信号作奇异值分解，分析并处理信号的奇异值，从而有效降低信号中噪声的影响。本文利用奇异值分解降噪对信号作预处理，为之后的载波频偏估计做准备。

设x(n),n=1,2,…,N是长度为N的一维信号采样序列，利用此序列可以构造矩阵：

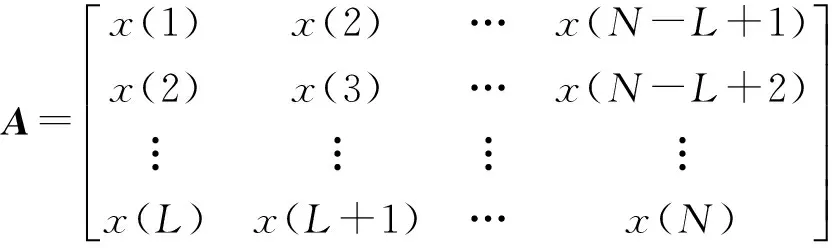
(12)

式(12)中，A为m×n维矩阵，利用式(2)对矩阵A做奇异值分解，获得一组非零奇异值。若原信号x(n)是由有效信号与噪声信号共同组成的，那么组成的矩阵A也同样是由有用信号和噪声共同构成。前几个较大的奇异值主要代表有效信号，其它奇异值则主要代表噪声，选取一个奇异值的阀值，将小于奇异值阀值即代表噪声的那部分置零则能够有效对原信号进行去噪。接着利用式(3)重构矩阵，将矩阵中各列的项值相加，再取平均值，最后就能够重构出去噪信号[14]。

重构信号即作为预处理后的信号，最后将其带入M&M频偏估计算法。将经过SVD预处理的频偏估计结果与直接进行频偏估计的结果进行对比，如果性能提升不明显，根据结果反馈进行分析并选取更好的奇异值阀值，重新进行计算，直到性能有所提升，将最优的奇异值阀值代入实际应用中。SVD-MM整体流程图如图2所示。

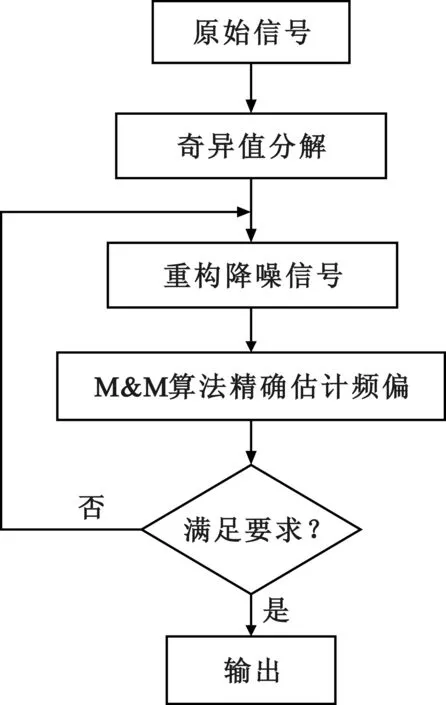
图2 基于SVD去噪的载波频偏估计流程

基于SVD降噪方法的实现实际是通过利用有用信号和噪声信号的相关性进行奇异值阀值的判断。当有用信号和噪声信号相关性较小时，奇异值阀值较为明确，判定噪声信号比较容易，去噪效果较好。当有用信号和噪声信号相关性较大时，说明两个信号混杂度较高，通过奇异值不能很好地进行判定。甚至在信噪比很低，噪声信号和有用信号相似甚至将其淹没时，SVD降噪功能失效。

3.2 性能评价标准

目前公认的评价频率估计方法的性能指标主要有估计均方根误差、估计方差、估计范围、计算复杂度、信噪比门限值等。均方根误差表明估计算法是有偏的还是无偏的，方差则用来表示估计算法的估计精确度。一个完美的频偏估计算法必然是无偏的并且方差很小。通常一个算法估计精度的标准用克拉美罗界[15](Modified Cramer-Rao bounds, MCRB)来表示，即估计方差越接近MCRB值，说明此算法的估计精度越高，是估计精度最好的情况。频偏估计的MCRB值可由式(13)得到：

(13)

式中，L0为观测的数据长度，T为采样周期，Es/N0为信噪比真值。可从关于方差的仿真图中大体判断出该算法工作的信噪比门限值。

估计范围也是一个很重要的指标，定义为f0/fs，即归一化频偏，f0为载波频偏，fs为采样频率。受奈奎斯特采样定理的限制，频偏的最大估计范围是(-0.5～0.5)。计算量在工程中影响实现复杂度，可通过算法的复乘法和复加法来分析。在实际情况下，计算复杂度与估计精度、估计范围等相矛盾，这是目前算法急需解决的问题之一。

4 仿真与分析

为了验证奇异值分解降噪算法的有效性，本文采用Matlab语言进行软件仿真。设置信号的采样频率为1 000 Hz；预设频偏为300 Hz；采样点数选取32、64、128这3种模型，在信噪比从-15～15 dB之间进行仿真。对比未预处理和预处理后频偏估计的均方根误差、方差和估计范围这3个性能，实验结果及性能分析如下。

4.1 估计精度

不同的模型长度，对应的仿真估计值接近真实值的速率也不一样。模型长度越长，在低信噪比时就能更快接近真实值，但是同时，计算的数据量也相应增大。如图3归一化均方根误差对比图所示，在L=128条件下，图3中未进行预处理的信号大约在-3 dB的时候接近真实值，但是进行了预处理的信号在-5 dB之前就能够接近真实值。其他采样长度的信号临界值也相应地有约2 dB的降低，更好的贴近了现实环境下的信号传输。并且从图3中可以看出，在相同仿真次数下，去噪后信号的仿真曲线更加平滑，在接近真实值附近信号波动减小，更加稳定地趋近于真实值。总体来说，去噪后的信号频偏估计性能在精确度上有所提升。

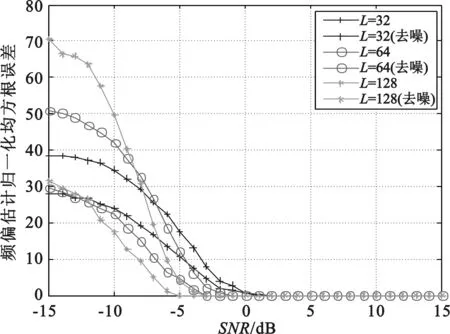
图3 信号分别未去噪和去噪后频偏估计归一化均方根误差对比

4.2 方差和信噪比门限

如图4所示，M&M算法频偏估计的信噪比门限值非常明确，高于门限范围的估计值极其接近MCRB，但是低于门限范围的估计值就极大地远离MCRB。在L=128的条件下，图4中未进行预处理的信号信噪比门限约为-2 dB；进行了去噪的信号信噪比门限约为-5 dB，降低了3 dB；其他采样长度下，信噪比门限也相应有大约2～3 dB的降低。并且在低于信噪比门限时，图4中进行了预处理的信号虽然远离MCRB，但是其相比于未预处理信号，归一化方差降低了约一个数量级，表示估计数据更加稳定。总体来说，去噪后的信号频偏估计性能在稳定性上有所提升。

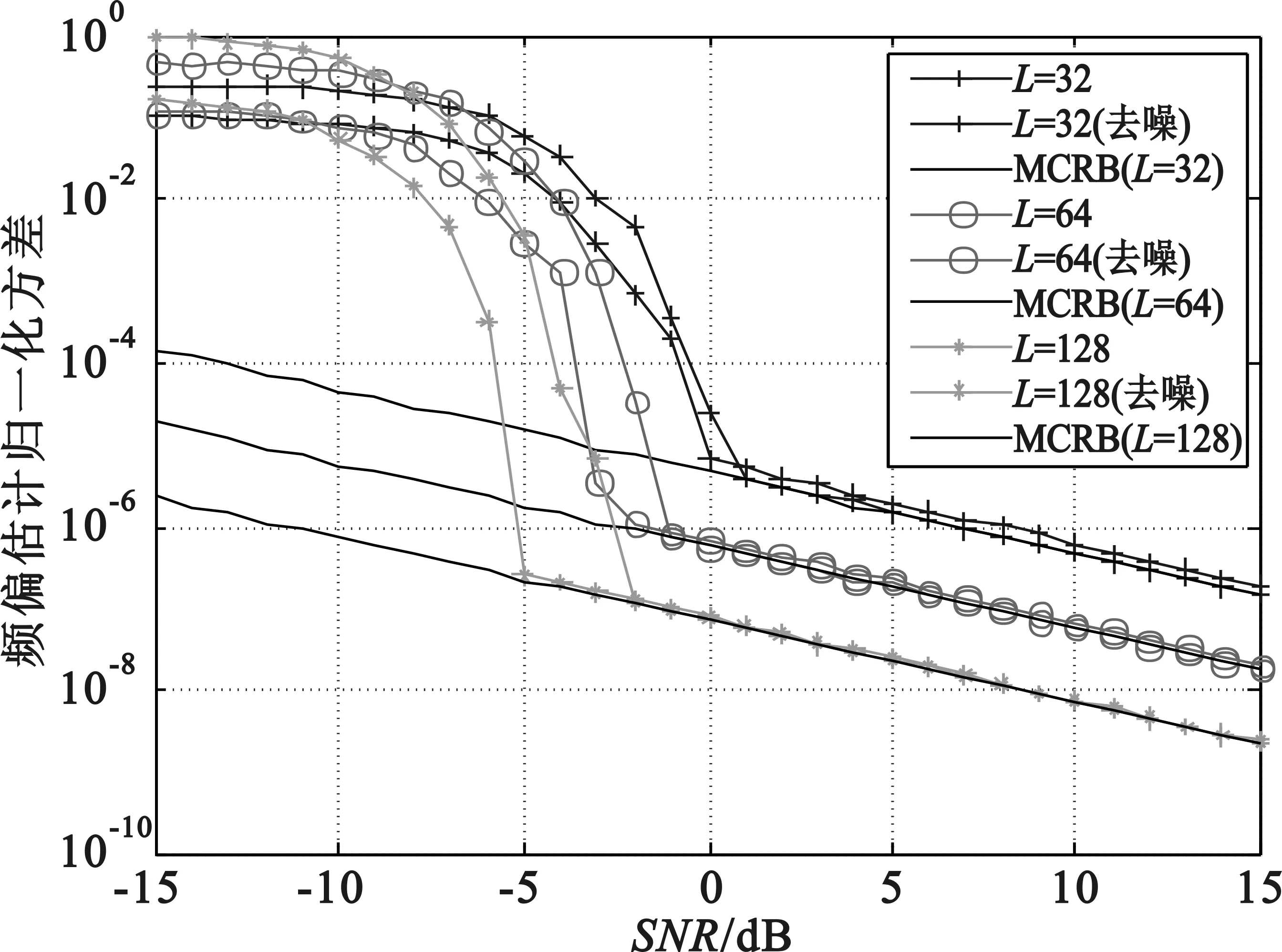
图4 信号分别未去噪和去噪后频偏估计归一化方差对比图

4.3 估计范围

如图5所示，进行了去噪预处理的估计范围比原估计范围有一定程度的提升。虽然去噪后的信号进行频偏估计，并没有改变M&M算法的原理和方式，但是新算法成功降低了信噪比门限，因此在新门限附近，原算法的估计范围已经极不稳定，而新算法依然能保持较大估计范围。M&M算法在频率与相位增量之间建立关系而不是直接在频率与相位之间建立关系的思想，相比于其他经典算法有着更高的估计范围[16]，因此新算法也有着相同的高估计范围。

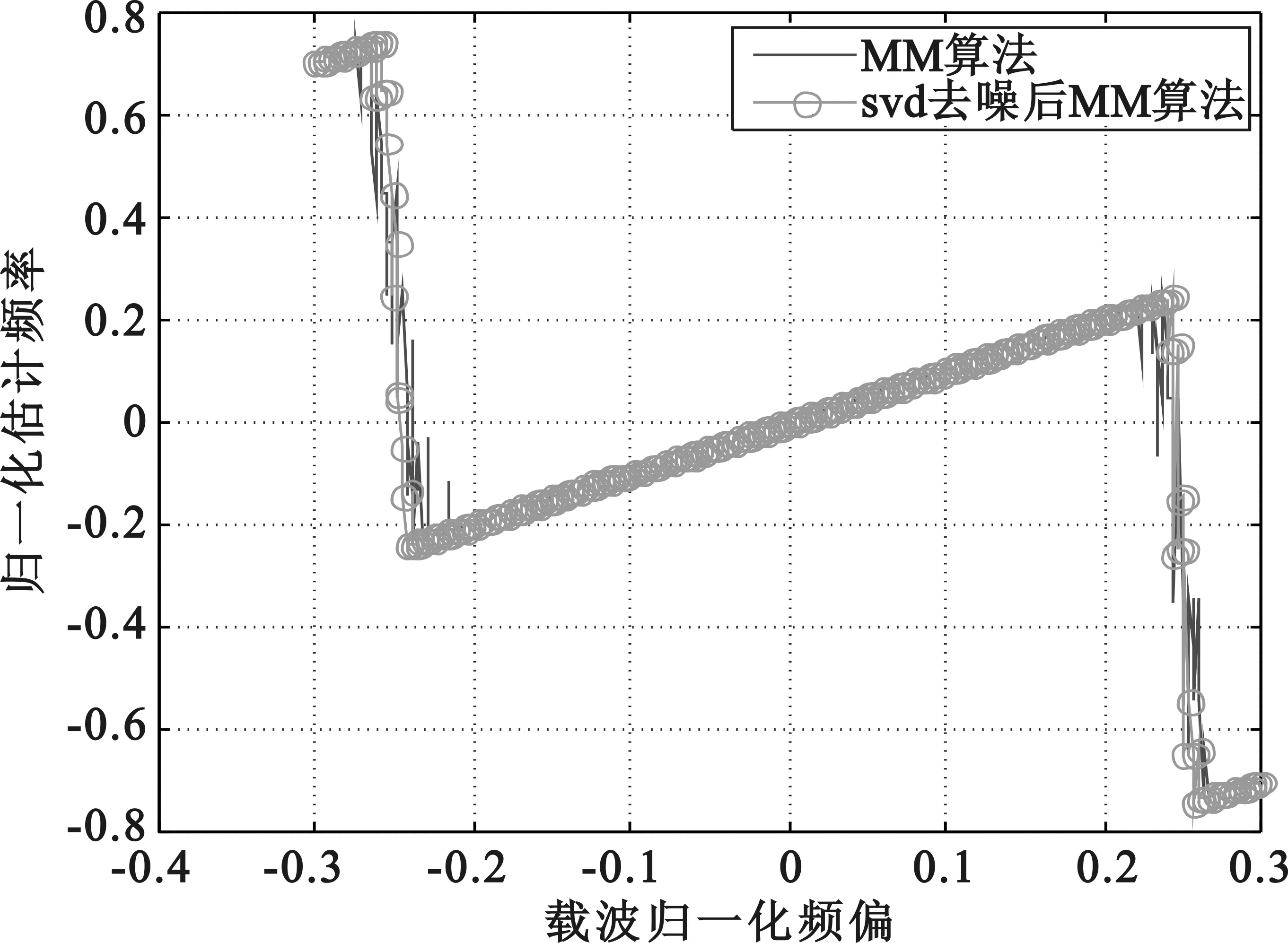
图5 信号分别未去噪和去噪后频偏估计归一化范围对比

5 结 语

论文首先利用奇异值分解技术对含有噪声的复信号进行降噪，再对预处理后的信号进行经典的M&M频偏估计。相比其它算法，本文提出的SVD-MM算法虽然计算复杂度有所增加，不过随着硬件处理能力的提高，利用FPGA等完成SVD去噪已经非常便捷，计算复杂度已不是制约算法性能的瓶颈。

通过Matlab仿真验证，该方法可以获得更低的信噪比门限、更低的差错概率，并基本保持原本较大的估计范围不变。在环境复杂、干扰因素较多的现实通信过程中，降低1dB甚至2dB的信噪比门限，对低信噪比环境下突发信号载波同步的实现意义重大，具有一定的实用价值。

[1] Rife D C，Vincent G A．Use of the Discrete Fourier Transform in the Measurement of Frequencies and Levels of Tones[J]．Bell Sys Tech J，1970，49(2)：197-228．

[2] Quinn B G．Estimating Frequency by Interpolation Using Fourier Coefficient[J]//IEEE Trans-SP，1994，42(5)：1264-1268．

[3] Kay S. A Fast and Accurate Single Frequency Estimator, IEEE Transactions on Accoustics,Speec,and Signal Processing,1989,37(2):1987-1989.

[4] Fitz M P. Planar Filtered Techniques for Burst Mode Carrier Synchronization[J].IEEE Globecom,1991,12(1):365-369.

[5] Luise M, Reggiannini R. Carrier Frequency Recovery in All-Digital Modems for Burst-Mode Transmissions[J].IEEE Transactions on Communications,1995,43(2):1169-1178.

[6] Mengali U, Morelli M. Data-Aided Frequency Estimation for Burst Digital Transmission[J]. IEEE Transactions on Communications,1997,45(1):23-25.

[7] 帅 涛，任前义，刘 静等. 一种适用于大频偏和低信噪比条件的频率估计器研究[J].宇航学报，2010，31(12):2741-2745. SHUAI Tao, REN Qian-yi, LIU Jing, et al. An Frequency Estimator for Large Frequency Offset and Low SNR Signals[J]. Journal of Astronautics, 2010，31(12):2741-2745.(in Chinese)

[8] 王甲峰，姚军，岳旸等. 基于高阶循环累积量的载波频率估计[J]. 通信技术，2010，43(08)：111-113. WANG Jia-feng, YAO Jun, YUE Yang, et al. Carrier Frequency Estimation based on High-Order Cyclic Cumulant[J]. Communications Technology, 2010，43(08)：111-113. (in Chinese)

[9] 蒋为. 一种基于相关系数的频率估计算法[J]. 微波学报，2012.4,28(02)：49-52. JIANG Wei. Algorithm of Frequency Estimation based on Correlation Coefficient[J]. Journal of Microwaves，2012.4,28(02)：49-52. (in Chinese)

[10] WANG Hong-wei，ZHAO Guo-qing．Improved Rife Algorithm for Frequency Estimation of Sinusoid Wave[J]．Signal Processing，2010，26(10)：1573-1576.

[11] 周磊磊，罗炬锋，付耀先等. 低信噪比下基于自相关函数的频率估计方法[J]. 华中科技大学学报：自然科学版，2014，42(04):45-49. ZHOU Lei-lei，LUO Ju-feng，FU Yao-xian，et al. Frequency Estimator based on Autocorrelation with Low SNR [J]. Journal of Huazhong University of Science and Technology(Natural Science Edition)，2014，42(04):45-49. (in Chinese)

[12] 刘晓冬，陈卫东.一种宽范围高精度的载波频偏估计算法[J]. 无线电工程，2014，44(03)：43-45. LIU Xiao-dong,CHEN Wei-dong. Carrier Frequency Offset Estimation Algorithm with Extended Range and High Accuracy[J]. Radio Engineering，2014，44(3)：43-45. (in Chinese)

[13] 郭强，吴杰，桑睿． 一种低信噪比下 PSK信号载波频率估计方法[J]． 电视技术，2012，36(07):93-96. GUO Qiang,WU Jie,SANG Rui. Rate-A Method of PSK Signal Carrier Frequency Estimation in Low SNR[J]. Video Engineering, 2012，36(07):93-96. (in Chinese)

[14] 钱征文，程礼，李应红. 利用奇异值分解的信号降噪方法[J]. 振动、测试与诊断，2011,31(04):459-463. QIAN Zheng-wen，CHENG Li，LI Ying-hong. Noise Reduction Method based on Singular Value Decomposition[J]. Journal of Vibration, Measurement & Diagnosis，2011,31(4):459-463. (in Chinese)

[15] D′Andrea A N, Mengali U and Reggiannini R. The Modified Cramer-Rao Bound and Its Application to Synchronization Problems[J]. IEEE Transactions on Communications, 1994, 42(2/3/4):1391-1399.

[16] 石盛超,索龙龙,张卫同.基于自相关函数的前向频率估计方法综述[J].电子质量，2012(12)：38-42. SHI Sheng-chao，SUO Long-long，ZHANG Wei-tong. Autocorrelation-based Feedforward Carrier Frequency Estimator[J].Electronics Quality，2012(12)：38-42. (in Chinese)

Research of SVD in Carrier Synchronization Technology

YANG Han-zhu，LI Guang-xia，ZHAO Lu-wen，ZHANG Jing-yi

(Communication Engineering College,PLA University of Science and Technology,Nanjing Jiangsu 210007,China)

In order to improve the performance of carrier frequency offset estimation algorithms in burst-mode communication, and reduce the SNR threshold in effective estimation, a new frequency offset estimation method based on singular value decomposition is proposed. Firstly, this method transforms the primal signal into matrix via a relevant reflection, and then implements singular value decomposition of the matrix. Secondly, the several fairly large singular values are determined as signal characteristic for reservation or otherwise as noise characteristic turning into zero. Thirdly, based on the new singular values the analog signals are reconfigured .Finally, M&M frequency offset estimation is done on the preprocess signals. Experiment results show that, as compared with traditional algorithm, the proposed method could raise the estimation precision, reduce the SNR threshold, and thus is of certain practical value.

burst-mode communication; frequency offset estimation; singular value decomposition

2015-04-01；

2015-07-20 Received date:2015-04-01；Revised date：2015-07-20

国家自然科学基金(No.91338201);中国博士后科学基金(No.2013M542485)

Foundation Item:National Natural Science Foundation of China(No.9133201);China Postdoctoral Science Foundation(No.2013M542485)

TN927.2

A

1002-0802(2015)09-1004-06

杨晗竹(1991—)，女，硕士研究生，主要研究方向为卫星通信、卫星导航等;

李广侠(1964—)，男，硕士，博士生导师，主要研究方向为卫星通信、卫星导航、卫星测控等;

赵陆文(1977—)，男，博士，讲师，主要研究方向为卫星通信、卫星导航、卫星测控等;

张敬义(1989—)，男，硕士研究生，主要研究方向为通信抗干扰。

10.3969/j.issn.1002-0802.2015.09.005