旋转轴为任意直线时旋转体体积的计算

孙成金， 张建军， 李战国

(河南农业大学 信息与管理科学学院，河南 郑州 450046)

旋转轴为任意直线时旋转体体积的计算

孙成金， 张建军， 李战国

(河南农业大学 信息与管理科学学院，河南 郑州 450046)

利用微元法的基本思想，给出了直角坐标方程、参数方程形式下的平面曲线绕一般直线旋转所得旋转体体积的计算公式．最后，利用矢量法可推到二维、三维旋转体体积的计算．

旋转体体积；微元法；曲边梯形；矢量公式法；参数方程

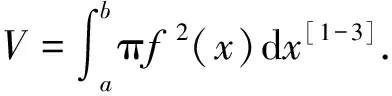
在数学计算本身以及对实际问题应用中具有一定意义的平面曲线绕任意一条直线旋转所生成旋转体的体积又如何计算呢？一个直观思路是：先通过平移和旋转坐标轴，求出曲线在新坐标系下的方程，将问题转化成新曲线绕新坐标轴旋转所得旋转体的体积计算．其实不然，这种思路的工作量非常大，有时甚至使一个简单的曲线函数y=f(x)变得非常复杂，很难进行数值计算．

为了数值计算和应用上的便利，本文利用微元法的基本思想[4-5]推导出平面曲线绕任意一条直线旋转所产生的旋转体体积的计算公式,该公式计算简洁，容易推广和应用．

1 直角坐标方程旋转体的体积计算

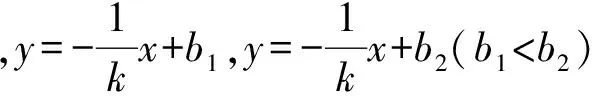
(1)

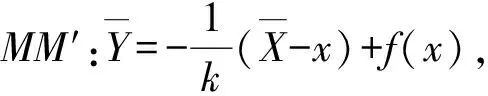
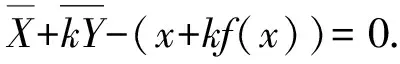
在区间[a,b]上任取一小区间[x,x+dx]，设相应于小区间[x,x+dx]的曲线段在直线L上的投影长为dl，当dx充分小时，切线MT上对应于右端点x+dx的点N(x+dx,f(x)+f′(x))到垂线MM′的距离即为dl,则

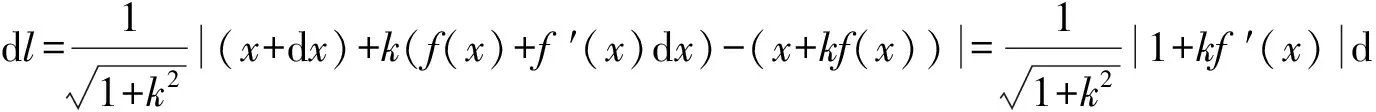
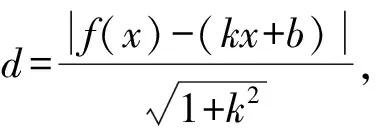
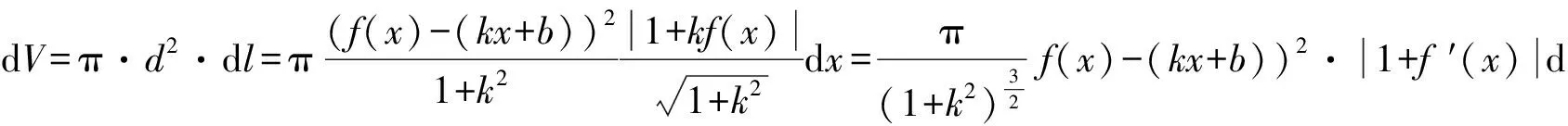
所以，

(2)

注1 公式(2)适用于曲边梯形的边界与直线L的任意一条垂线只有一个交点的情况，若曲边梯形的边界与L的垂线交点多于一个，则只需将曲边梯形化为若干个区域计算即可．

注2 若直线L的方程为Ax+By+C=0，则

例1 计算曲线y=x2与直线y=mx(m>0)在第一象限内所围成的图形绕该直线旋转所生成旋转体的体积．

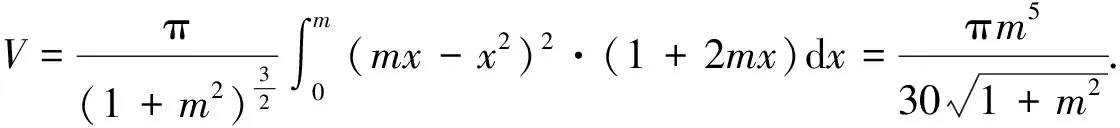
2 参数方程旋转体的体积计算

(3)

证明 任意取一点t∈[a,b]，给参变量t一个增量Δt，使得t+Δt∈[a,b]，曲线L上相应于t与t+Δt的点坐标为M(x,y)，N(x+Δx,y+Δy)，直接计算得M，N在直线l上的投影M′，N′的坐标为

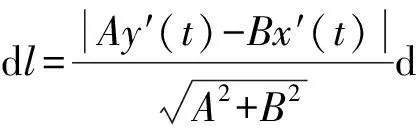
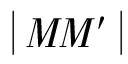
解 由已知，y′(t)=4，x′(t)=2.区间为(0,m)，利用公式(3)有

3 参数方程旋转体的矢量公式求体积

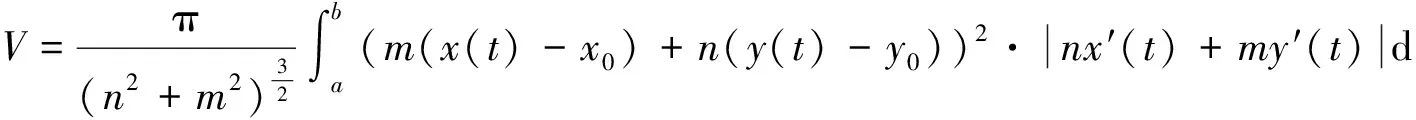
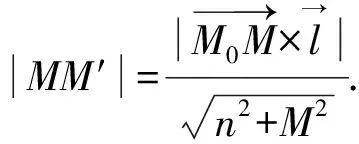
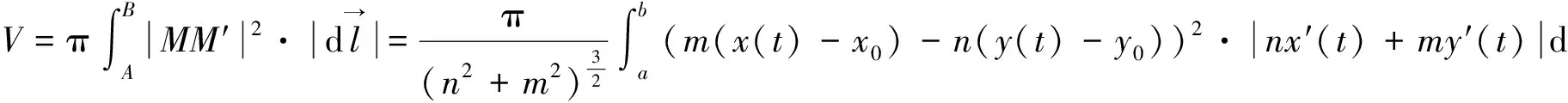
对于空间情形有如下推广定理：

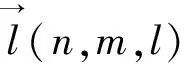
(4)

注3 定理4中，当l=0,z(t)=0,z0=0时，(4)式即为定理3的结论．

如果将例2中的直线l改成相应的矢量形式的直线方程，利用矢量公式法求得的结果是一样的．

4 结语

本文给出了一般曲线绕平面内任意一条直线旋转时所得旋转体体积的计算，给出了不同曲线函数形式绕直线旋转所得旋转体体积计算公式，如果把公式中旋转体的对称轴换成坐标轴，可以直接使用此公式计算一般教材中曲线绕坐标轴旋转所得旋转体计算公式，具有一定的计算应用意义．当然仍可在多维空间中继续推广，有待深入研究．

[1] 同济大学数学教研室.高等数学[M]．北京：高等教育出版社,2007:272-292.

[2] 华东师大数学系.数学分析[M]．北京：高等教育出版社,1980:303-307.

[3] 梁保松，陈涛.高等数学[M]．北京：中国农业出版社，2013:151-160.

[4] STEVEN R.Lag, conves sets and their application[M]．Newyork: Dover Publications, 2007: 146-159.

[5] 姬利娜，郑群珍.化归思想在常微分方程教学中的应用[J]．河南教育学院学报：自然科学版，2012,21(1):53-54.

Discussion on the Calculation of Rotary Body’s Volume for Axis of Rotation Arbitrary Line

SUN Chengjin， ZHANG Jianjun， LI Zhanguo

(CollegeofInformationandManagementScience,HenanAgriculturalUniversity,Zhengzhou450046,China)

Based on the basic idea of differential element method, the calculation formula of the rotating body’s volume generated by the rotation of a plane curve around general linear in the form of rectangular coordinates equation and parametric equation is given. At last, the calculation formula of the volume is applied to the calculation of the volume of two-dimensional and three-dimensional rotating body by vector method.

volume of rotating body; infinitesimal dividing method; curved edge trapezoid; vector formula method; parametric equation

2015-09-28

河南省高等学校重点科研项目(15A110028)；河南省教育厅科学技术研究重点项目(13A210485)

孙成金(1978—)，男，山东临沂人，河南农业大学信息与管理科学学院讲师．

10.3969/j.issn.1007-0834.2015.04.017

O172.2;G642.0

A

1007-0834(2015)04-0062-03