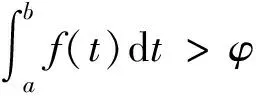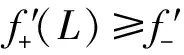严格单调增加HG凸函数的定积分下界
时统业, 沈湘洮, 宋祥斌
(海军指挥学院 信息系,江苏 南京 211800)
严格单调增加HG凸函数的定积分下界
时统业, 沈湘洮, 宋祥斌
(海军指挥学院 信息系,江苏 南京 211800)
考虑严格单调增加的HG凸函数,也即其反函数的倒数是GA凸函数的严格单调增加的函数.利用GA凸函数的性质,用普通的数学分析方法,给出这类函数定积分的下界.
单调函数;反函数;HG凸函数;积分不等式;单侧导数;下界
0 引言

ALZER H在文献[1]给出如下结论:
定理1 设b>a>0,f:[a,b]→R为严格单调增加的函数,1/f-1为凸(凹)函数,则
(1)
文献[2]给出比式(1)略强的结果:
定理2 设b>a>0,f:[a,b]→R为严格单调增加的函数,1/f-1为凸(凹)函数,则
一个很自然的问题就是,如果1/f-1为其他类型的凸函数,会有怎样的结果.本文考虑严格单调增加的函数f:[a,b](0,∞)→(0,∞),且1/f-1为GA凸函数.从GA凸函数的定义出发,容易证明这类函数即严格单调增加的HG凸函数[3].本文仿照文献[2]和[4]的方法来给出这类函数定积分的下界.
定义1[5]设f(x)是定义在区间I⊂(0,∞)上的连续函数,如果对于任意x1,x2∈I和t∈(0,1),有
(2)
则称f(x)在区间I是GA下凸的.若式(2)的不等式是严格的,则称f(x)在区间I是严格GA下凸的.
定义2[3]设区间I(0,∞),f:I→(0,∞),若对任意x1,x2∈I和t∈(0,1),有
(3)
则称f(x)是区间I上的HG凸函数.如果式(3)中的不等号反向,则称f(x)是区间I上的HG凹函数.
引理1[4]设f:I(0,∞)→R是GA下凸函数,则f在每一处都存在单侧导数,且成立.
引理2[6]设f(x)是[a,b](0,∞)上的GA下凸函数,则:1)和(x)在(a,b)单调不减;2) 对任意x,y∈(a,b),有

引理3 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,则f的单侧导数存在,且对任意x,y∈(a,b),x (4) 证明 因为1/f-1是[f(a),f(b)]上的(严格)GA凸函数,由GA凸函数的定义可证f是HG凸函数,又由文献[3]知f(x-1)是[b-1,a-1]上的对数凸函数,且由文献[4]知对数凸函数的单侧导数存在,f(x)是由f(u-1)和u=x-1复合而成,从而f在(a,b)内的单侧导数存在. 不妨设u=f(x),v=f(y),则u 注2 利用HG凸函数与对数凸函数的关系(文献[3]定理1)也可证明引理3. 引理4 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,u,w∈[a,b],u (5) (6) (7) 证明 由引理2容易证明(5)、(6),这里略去.由式(5)得 (8) 又由引理3有 (9) 由式(8)、式(9)得式(7). 定理3 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,c∈[a,b]则有 (10) (11) 其中, 证明 由引理4有 (12) (13) 式(12)除以t2,然后在[a,c]上对t积分得 (14) 同理可得 (15) 式(14)和式(15)相加即得式(10).类似地从式(12)和式(13)出发,可证得式(11).当1/f-1是严格的GA凸函数时,式(12)和式(13)至少有一个是严格的,所以式(10)和式(11)是严格的. 推论1 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,c∈(a,b),f在点c处可导,f′(c)≠0,则有 推论2 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,则当时,分别有 定理4 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上严格的GA凸函数,对任意x,u,w∈[a,b],u 则有 (16) 证明 由引理4得 (17) (18) 当1/f-1是严格的GA凸函数时,式(17)和式(18)至少有一个是严格的,所以式(17)和式(18)相加得 还需证明φ(u,w,x)在x=x0(u,w)处取得最大值. 可以断言u 故u (19) 由推广的Cauchy中值定理[7],存在ξ∈(u,w)及p≥0,q≥0,p+q=1,使得 由引理3有 于是有式(19)成立. 推论3 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上严格的GA凸函数存在,则有 (20) 证明 在定理4中取u=a,w=b,则式(20)的第一个不等式得证,分别取x=a,x=b,则式(20)的第二个不等式得证. 定理5 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上严格的GA凸函数,c∈(a,b),记 则有 (21) 证明 由引理4得 (22) (23) 当1/f-1是严格的GA凸函数时,式(22)和式(23)至少有一个是严格的,所以式(22)和式(23)相加得 定理6 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,则有 (24) 等号成立当且仅当存在正的常数p1,p2,q1,q2使得 证明 设c∈(a,b),由引理4,对任意t∈[a,b],t≠c,有 (25) (26) 式(25)、式(26)分别在[a,c]和[c,b]上对t积分并相加得 在上式中取c=A,则上式化为式(24).从证明过程可知,式(24)等号成立,当且仅当式(25)和式(26)分别在[a,A]和[A,b]上等号成立,定理得证. 推论4 若f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,则有 (27) 等号成立,当且仅当存在正的常数p,q使得f(t)=pq1/t. 注3 若f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,则利用引理3和引理4可证tlnf(t)是[a,b]上的凸函数,由Hermite-Hadamard不等式也可得到式(27). 定理7 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,则有 (28) 等号成立,当且仅当存在正的常数p1,p2,q1,q2使得 证明 由引理4,对任意t∈[a,b],t≠c,有 (29) (30) 式(29)、式(30)分别在[a,L]和[L,b]上对t积分并相加得式(28).类似于定理6可得等号成立的条件. 推论5 设f:[a,b](0,∞)→(0,∞)是严格单调增加的函数,1/f-1是[f(a),f(b)]上的(严格)GA凸函数,则有 (31) 等号成立,当且仅当存在正的常数p,q使得f(t)=pq1/t. [1] ALZER H.On an integral inequality[J].Math Rev Anal Numer Th Approxim,1989,18:101-103. [2] CHU YUMING,ZHANG XIAOMING,TANG XIAOMING.An upper bound estimate for H. Alzer’s integral inequality[J].Sarajevo Journal of Mathematics,2008,4(17):191-196. [3] 陈少元,宋振云.HG凸函数及其Jensen型不等式[J].数学的实践与认识,2013,43(2):257-264. [4] 张小明,褚玉明.解析不等式新论[M].哈尔滨:哈尔滨工业大学出版社,2011:180-198. [5] 吴善和.GA-凸函数与琴生不等式[J].贵州师范大学学报:自然科学版,2004,22(2):52-55. [6] 时统业,吴涵.GA凸函数的若干不等式[J].湖南理工学院学报:自然科学版,2012,25(2):7-11. [7] 冯媛,冯国.推广的微分中值定理[J].高等数学研究,2010,13(5):61-62. Lower Bounds of Definite Integral for Strictly Monotonically Increasing HG-Convex Functions SHI Tongye, SHEN Xiangtao, SONG Xiangbin (DepartmentofInformation,PLANavalCommandCollege,Nanjing211800,China) The strictly monotonically increasing HG-convex functions are considered. Lower bounds of definite integral are obtained by using the properties of GA-convex functions and ordinary mathematical analysis method. monotonic function; inverse function; HG-convex function; integral inequality; unilateral derivative; lower bound 2015-06-08 时统业(1963—),男,河北张家口人,海军指挥学院信息系副教授,主要研究方向:基础数学教学. 10.3969/j.issn.1007-0834.2015.04.001 O178 A 1007-0834(2015)04-0001-06


1 主要结果