平衡损失下多元回归模型最优平衡估计及其性质

马改杰， 叶晓枫

(华北水利水电大学 数学与信息科学学院，河南 郑州 450000)

平衡损失下多元回归模型最优平衡估计及其性质

马改杰， 叶晓枫

(华北水利水电大学 数学与信息科学学院，河南 郑州 450000)

结合平衡损失函数的概念，在平衡最小二乘估计的基础上提出了一个对多元回归模型参数的新的估计，并讨论该估计的可容许性和无偏性.

多元回归模型；平衡损失函数；最优平衡估计；可容许性；无偏性

1 主要研究内容

本文讨论多元回归模型，希望运用平衡损失函数的思想[1]，并通过借鉴徐兴忠、吴启光[2]、罗汉[3]在平衡损失下对一元线性模型的研究成果，具体地构造一个多元回归模型回归系数的线性估计，并且研究该估计的可容许性、无偏性的特征.

先给出关于一元线性模型的概念和一些结论.

一元线性模型

(1)

其中Y为n维观测向量，X∈Rn×p且列满秩，β∈Rp和σ2>0为未知参数.徐兴忠、吴启光在平衡损失函数下研究了该模型回归系数的线性容许性问题.在研究模型(1)的参数β的估计问题时，最小二乘法的地位不容忽略.罗汉注意到平衡损失函数的优点，从而研究了在平衡损失函数下的最小二乘法，并将其称为平衡LS估计.

定理1 线性模型(1)中参数β的平衡最小二乘估计为

(2)

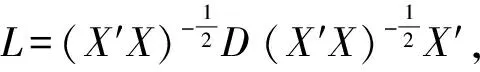
本文考虑多元线性模型

(3)

现在讨论模型(3)中平衡损失下未知参数Θ的估计问题，希望采用的方法是应用矩阵向量化运算，把模型(3)转化为一元线性模型，然后应用一元线性模型下平衡最小二乘估计的结果，导出Θ的估计.

应用Vec(ABC)=(C′⊗A)Vec(B)，有

Vec(Y)=(I⊗X)Vec(Θ)+Vec(ε)，

(4)

于是可以导出一个估计

Θb=[t(X′X-Ip)+Ip]-1[t(X′-L)+L]Y，

称该估计为平衡损失下多元回归模型最优平衡估计.

2 主要结论

首先，主要研究最优平衡估计的可容许性问题.在给出主要结论之前，先了解一下相关的两个引理.

接下来将给出关于最优平衡估计可容许的主要结论.

最后我们考察最优平衡估计Θb的另一性质，即无偏性，给出另外一个主要结论.

定理3 对于多元线性模型(3)，其最优平衡估计Θb=[t(X′X-Ip)+Ip]-1[t(X′-L)+L]Y为参数Θ的无偏估计的充分必要条件是LX=Ip.

3 主要结论的证明

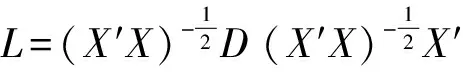
再根据Θb=[t(X′X-Ip)+Ip]-1[t(X′-L)+L]Y的导出过程知，在模型(4)中，{Iq⊗[t(X′X-Ip)+Ip]-1[t(X′-L)+L]}Vec(Y)为未知参数Vec(Θ)的可容许估计，即{Iq⊗[t(X′X-Ip)+Ip]-1[t(X′-L)+L]}Vec(Y)～Vec(Θ)，并且

(必要性)因为引理1及引理2中结论的条件都为充分必要条件，并且Θb的导出过程是可逆的，由充分性的证明可知，逆之必然成立，必要性得证.

定理3的证明 由模型(3)知，E(Y)=E(XΘ+ε)=XΘ，因此，

E(Θb)=[t(X′X-Ip)+Ip]-1[t(X′-L)X+LX]Θ=

[t(X′X-Ip)+Ip]-1[tX′X+(1-t)LX]Θ=[tX′X+(1-t)Ip]-1[tX′X+(1-t)LX]Θ，

所以，Θb为参数Θ的无偏估计，即对∀Θ∈Rp×q，E(Θb)=Θ的充要条件是

[1] ZELLER A. Bayesian and non-Bayesian estimation using balanced loss function[M]. Statistical decision theory and topics：V，1994:377-390.

[2] 徐兴忠,吴启光.平衡损失下回归系数的线性容许估计[J].数学物理学报,2000, 20(4): 468-473.

[3] 罗汉,柏超.线性模型中参数的平衡LS估计及其性质[J]. 湖南大学学报:自然科学版,2006,33(2):122-124.

[4] 曹明响,孔繁超.多元线性模型中回归系数的线性可容许估计[J].数学研究, 2009, 32(5):951-957.

Optimal Balance Estimate of Multivariate Linear Model Under Balanced Loss Function and Its Properties

MA Gaijie， YE Xiaofeng

(SchoolofMathematicsandInformationScience,NorthChinaUniversityofWater
ResourcesandElectricPower,Zhengzhou450000,China)

Integrating the concept of balanced loss function, a new estimation method of multiple regression model parameters is proposed on the basis of least square balance estimation, and the necessary and sufficient condition of the estimation in admissibility and unbiasedness are discussed.

multivariate regression model parameters; balanced loss function; optimal balance estimate;admissibility; unbiasedness

2015-09-17

马改杰( 1988—) ，女，河南开封人，华北水利水电大学数学与信息科学学院在读硕士研究生.

10.3969/j.issn.1007-0834.2015.04.003

O212.1

A

1007-0834(2015)04-0010-03