基于灰理论的汽车覆盖件成形优化方法

梁 丰，陈剑锋

LIANG Feng1, CHEN Jian-feng2

（1.河源职业技术学院 机电工程学院，河源 517000；2.广州本田汽车有限公司 黄埔区模具生产部，广州 510700）

0 引言

汽车钣金覆盖件是具有复杂的造型、整体尺寸较大的一类薄壁钣金件，由于其加工进程中复杂的金属流动和应力应变状态，无法对模具设计与冲压工艺参数进行理论公式计算，一般是凭借设计人员的经验根据结果反馈不断的调整参数、修模，最终达到满意效果。这种传统的汽车覆盖件成形方法耗时长，甚至有可能由于设计者经验不足导致昂贵的汽车模具报废。为了提升设计效率和降低成本，有限元技术被大量运用在汽车覆盖件的开发上[1～3]，为模具设计与冲压工艺参数设置提供了有效的指导。

灰理论是基于数理系统工程的交叉学科，它重点研究外部确定，内涵模糊的事件，具有分析影响因子与响应目标关联度大小的功能，能对系统的优化进行预测[4]。本文以汽车翼子板为例阐述优化方法，以有限元数值模拟为试验基础，结合灰理论的邓氏关联度优化算法，计算出如压边力、拉深筋高度等参数的最佳组合，达到对产品起皱、破裂、变薄严重等质量缺陷进行控制的目的。

1 基于灰理论的邓氏关联度优化方法

邓氏关联度算法是采取对收集序列矩阵数学关系的对比来分别系统中众多影响因素的联系程度，用于表达影响因子和响应之间变化趋势的关联程度。邓氏关联度越大，表明研究对象和选择的标准参考矩阵相似性越强。在对翼子板的成形质量分析中，涉及到多工艺参数的综合作用，由于这些不同的参数有不同的量纲和数量级，需对原始数据进行初值化、累加求和处理。

设X0：标准参考矩阵，Xi：目标数据矩阵。

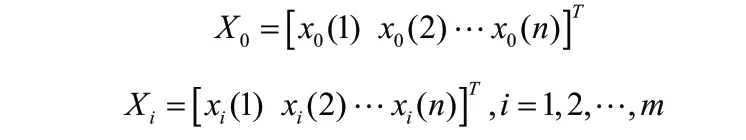
其中n为每个工艺影响因素的数据个数，m为影响产品品质的工艺影响因素个数。对Xi进行无量纲化处理，得到无量纲数据采取初值化法如式(1)所示，累加求和法如式(2)所示：

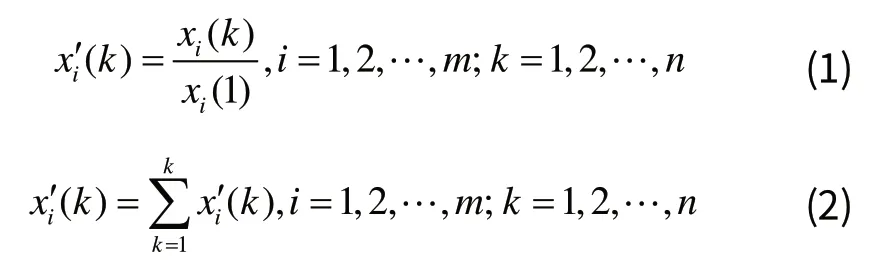
根据邓氏关联度算法[5]，Xi对于X0的k位置灰色理论关联数为：

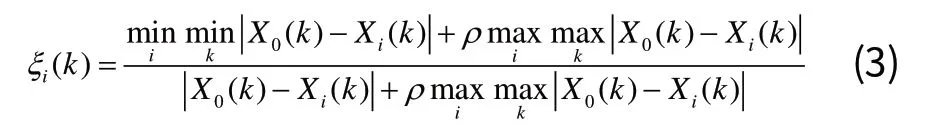
其中：ρ为取值在（0,1）之间的分辨系数，越小说明分辨力越大，一般取0.5。

由于关联度系数为对比目标矩阵和标准矩阵在不同时间的关联程度值，个数太多使信息不集中不利于进行整体分析，因此一般会求算目标矩阵对于标准矩阵的灰色理论关联程度：

2 定义优化模型

2.1 评价目标

汽车覆盖件的成形质量评价目标较多，根据本文翼子板成形过程中主要出现起皱、拉裂和厚度变薄严重的缺陷，定义三个评价目标：

h1：描述冲压发生破裂的极限点到安全裕度的距离，如图1所示。

h2：描述冲压发生起皱极限点到起皱极限的距离，如图1所示。

Δ：厚度的最大变薄率。

为了得到优良的产品质量，优化过程就是通过有限元分析软件DYNAFORM计算3个评价目标最小值时所对应的工艺参数。

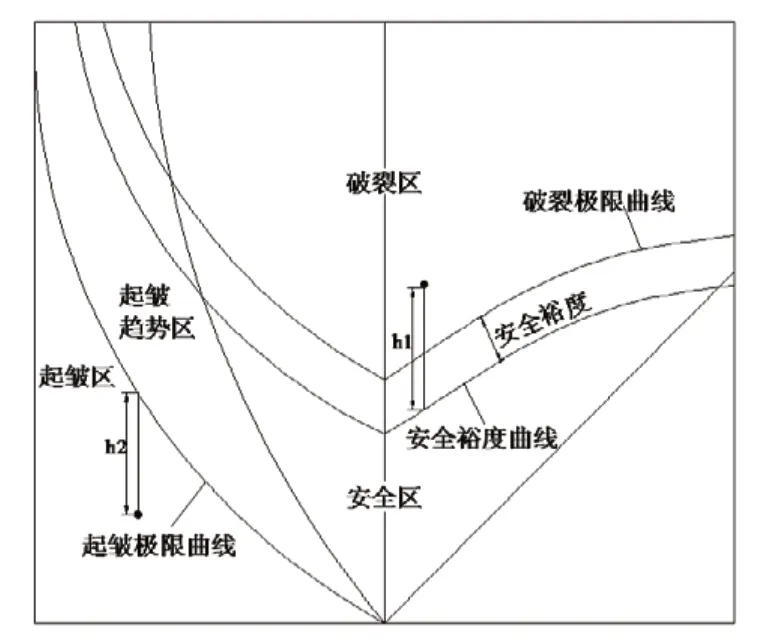
图1 成形极限图

2.2 工艺参数

影响响应目标的影响因素较多，为了使研究问题清晰，需确定对响应目标影响强烈的影响因素，根据汽车覆盖件冲压技术研究[6～8]，结合经验选择工艺参数为：压边力F、拉延筋的高度H、凹模入口半径R1和凸筋半径R2，如图2所示。通过灰理论优化方法计算出最小状态的评价目标，进而获取对应的4个最佳工艺参数数据组合，达到控制产品质量的目的。

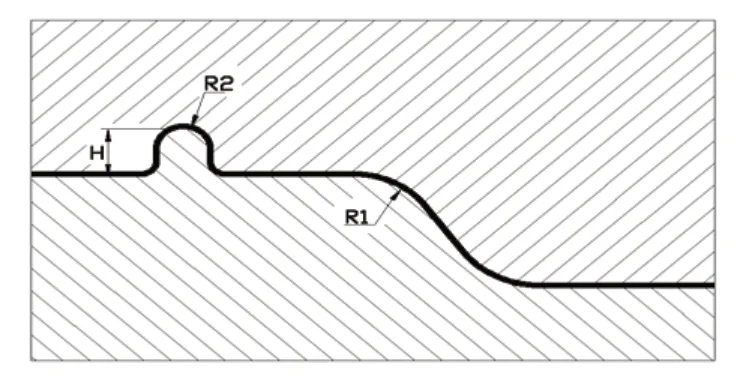
图2 工艺参数的定义

3 建立翼子板数据模型

翼子板材料是ST16钢材，对应DYNAFORM中T36号模型，厚1.0mm，其密度为7.85kg/m3，杨氏模量为2.05×105N/mm2，屈服极限是203MPa，泊松比是0.28，硬化指数是0.24，各向异性指数r=1.7，材料的应力-应变曲线如图3所示。

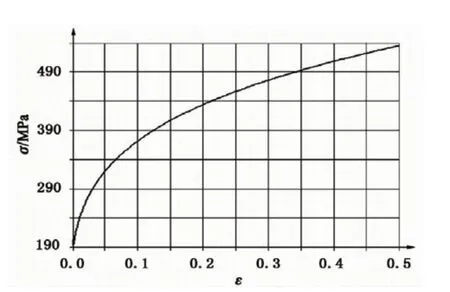
图3 应力-应变曲线

翼子板整体尺寸约为892×715×146mm，去除后续折弯的部分，对其孔和边缘进行工艺面补充，使模型边缘平滑过渡，为了使材料得到较大的流动阻力设置凸圆形拉深筋。网格采取四边形B-T薄壳单元，尺寸范围在[5,20]之间，为了保证有限元模型的精度，网格单元的内角>5°，空间曲度<3°。由于翼子板设计出的凹模直壁口部基本处在一个水平面上，因此压料采取平面压边圈。通过去除重叠单元，调整冲压方向，翼子板模具模型被离散成17805个单元，16248个节点，如图4所示。

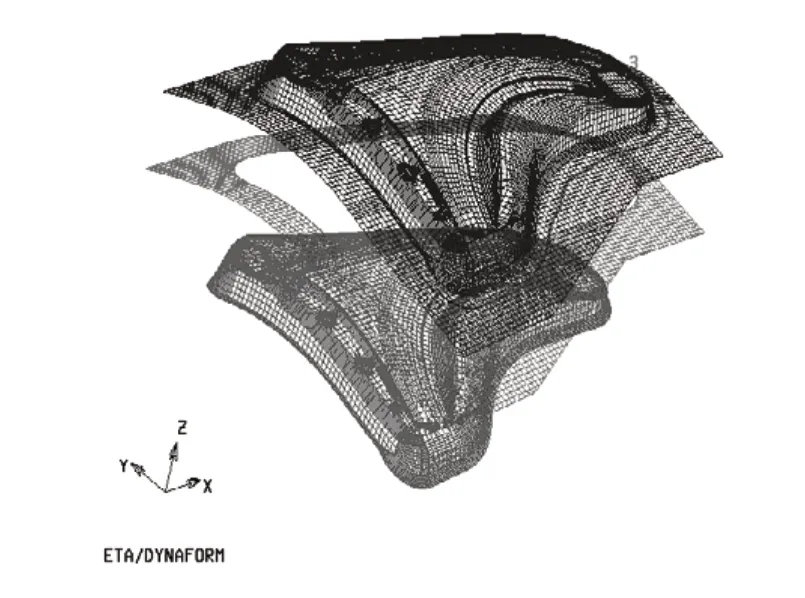
图4 翼子板模具有限元模型

4 基于数值模拟的正交试验设计

在以F、R1、H和R2为变量，以h1、h2、Δ为目标进行正交试验之前，需设置模拟的前提条件。依据现有研究与实践确定凹模下行速度为4m/s，摩擦系数为0.12。对影响因素进行4水平安排（如表1所示），利用正交表L16（45）进行试验，利用金属钣金成形有限元软件DYNAFORM 5.5进行分析，把16次验计算结果记录整理成表2数据。

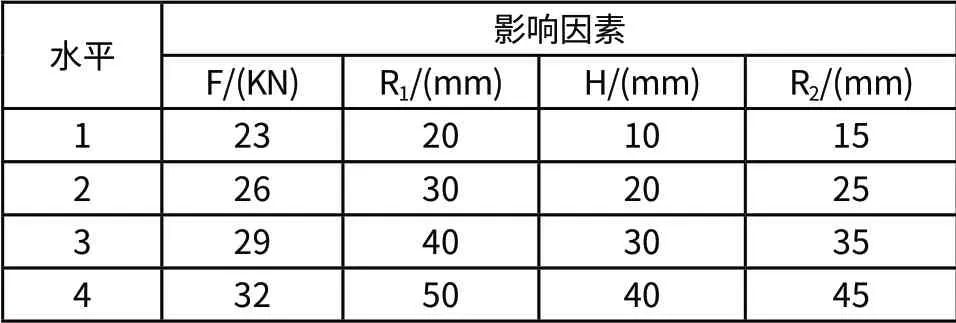
表1 影响因素设置

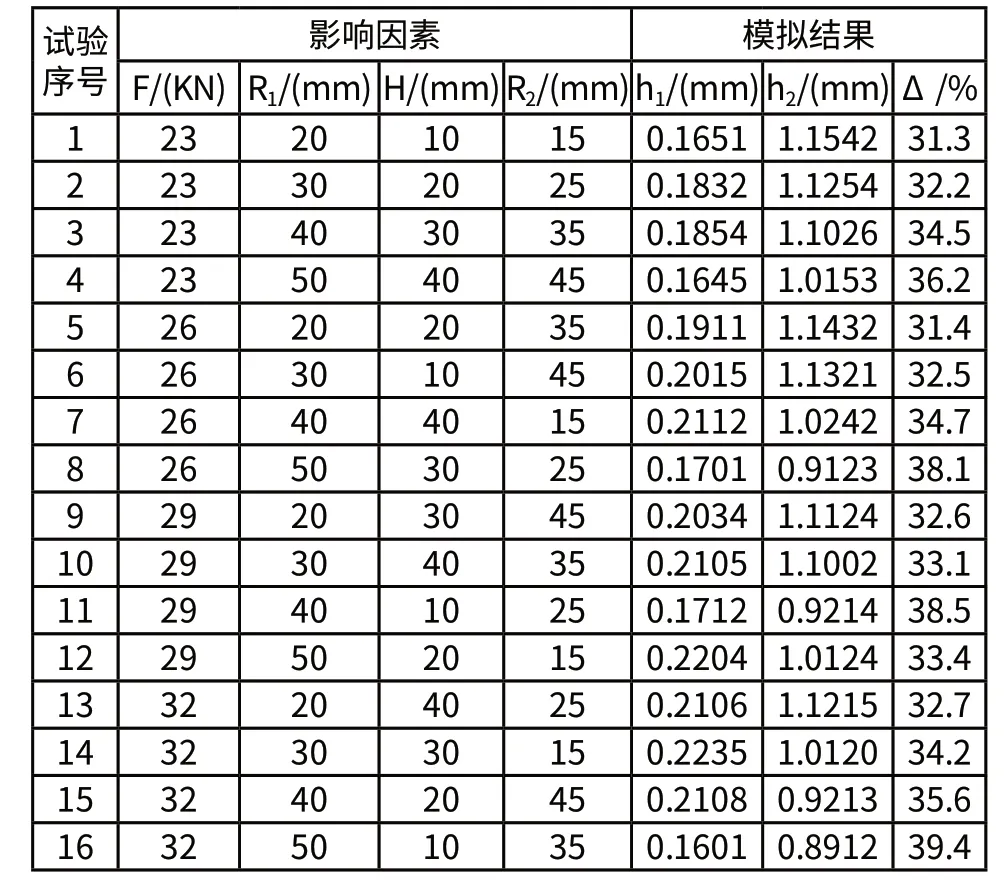
表2 正交试验安排及模拟结果

5 灰理论关联优化方法

5.1 灰关联系数计算

对表1中的3个评价目标数据进行无量纲化，首先进行初值化，如式(1)所示，再运用式(2)进行累加求和，为了得到简洁的数据，再次进行初值化，最终生成无量纲的数据列。运用式(3)进行各数据的关联系数，得到表3关联系数。

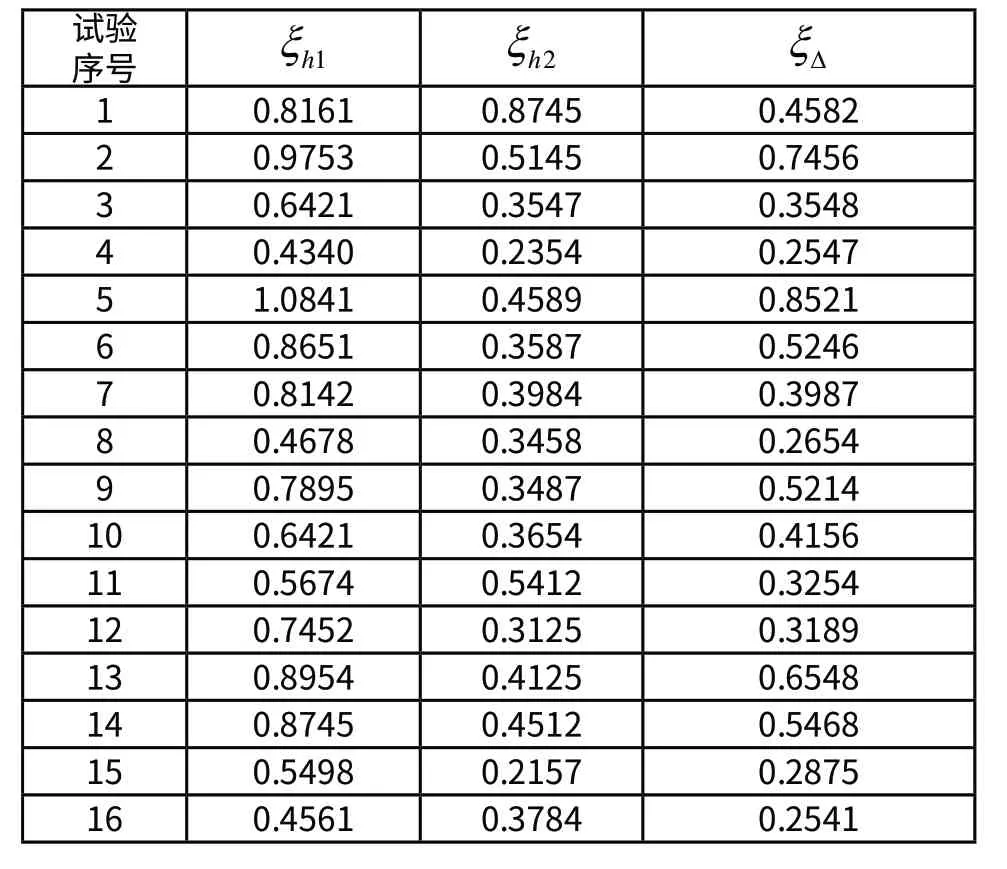
表3 评价目标的灰关联系数

5.2 灰关联度计算

合格产品要求没有拉裂、起皱和厚度变薄严重，因此3个评价目标的设计权重一致，都为1/3，运用式(4)进行评价目标的关联度计算，得到表4。对表4进行影响因素的平均关联程度运算，即把所有影响因素每一个水平相应的关联程度进行求和、均化。影响因素对某个水平关联程度大，说明影响因素在该水平越优化[9]，即对响应目标越好，根据表4计算各影响因素水平的均化关联程度如表5所示。其中代表压边力F的水平最大关联度为0.1895，对应水平为F=26kN，同理，凹模入口半径R1=20mm，拉延筋高度H=20mm，凸筋半径R2=15mm，它们构成了保证三个评价目标值最小的最佳工艺组合。

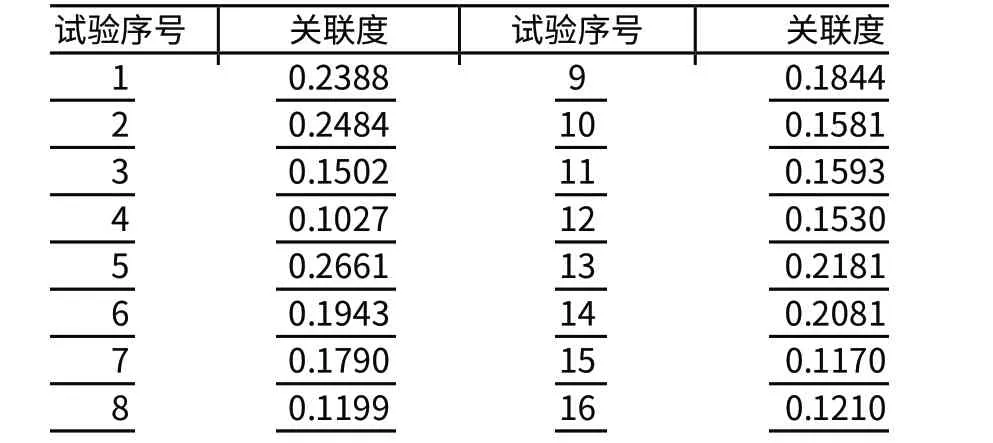
表4 评价目标的关联度

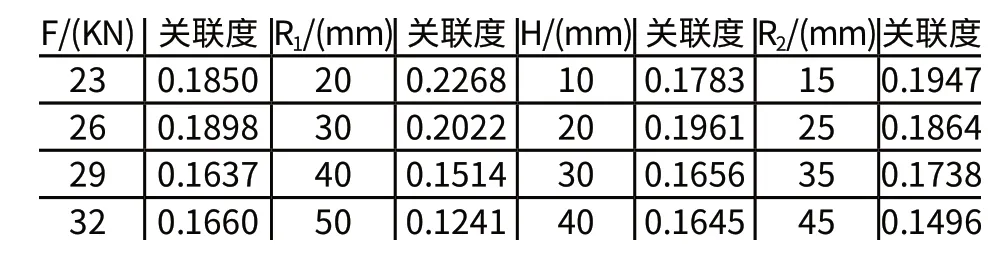
表5 工艺参数水平的平均关联度

6 数值模拟验证

依据上述方法获得的最佳工艺组合变更对应的数据，在其他参数不变的前提下重新以DYNAFORM为工具进行模拟计算。对比优化前后的成形极限图5、图6，可以明显的看出网格单元的主次应变布局更合理，单元应变点基本出现在安全区域内，h1和h2两个评价指标都比优化前小，使钣金在生产过程中不出现起皱与拉裂问题。对比优化前后的厚度分布云图，优化后的如图7所示，厚度最大变薄从25.34%减少到了14.25%，使产品强度得到保证。

图5 优化前的成形极限图

图6 优化后的成形极限图

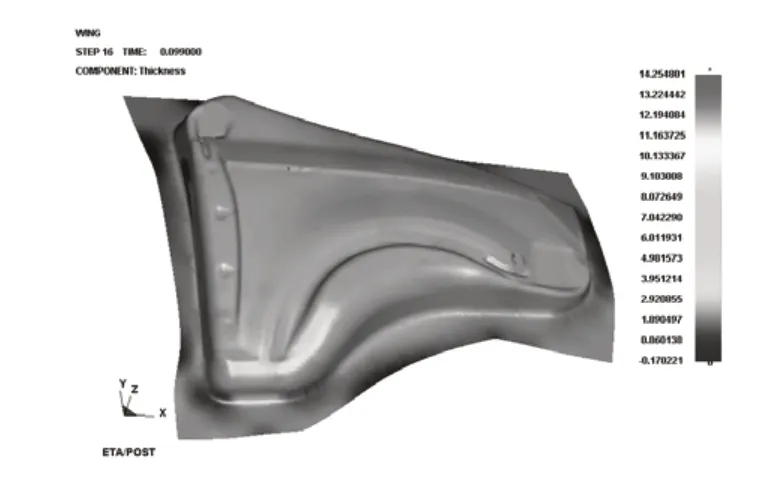
图7 产品厚度分布云图

7 结论

1）为了微观表达覆盖件成形质量的好坏，可对其建立评价模型，借助成形极限图定义反映拉裂程度、起皱程度和最大变薄程度的评价目标，以压边力、凹模入口半径、拉延筋高度和凸筋半径为影响因素进行正交试验，获取对应的评价目标数据。

2）通过基于灰理论算法，把非单一响应目标优化化归成单响应目标优化，利用运算影响因素平均关联程度，该数据越大，表明影响因素的该水平越逼近优化值，从而得到最佳的数据组合。

3）以DYNAFORM有限元分析软件为正交试验数据获取和验证工具，输入最佳的工艺组合进行计算，获得评价目标数据明显变小，说明加工质量进行了有效的提升。

[1] 杨丽娟.基于有限元技术汽车覆盖件的拉深成形仿真分析[J].铸造技术.2013.06:753-755.

[2] 任秀芬,章志兵,李贵,等.基于有限元模拟的汽车覆盖件滑移线预测算法[J].塑性工程学报.2011.01:11-15.

[3] 李春光,胡平,郭威.汽车覆盖件深拉延有限元仿真过程中的材料塑性与失效模型[J].吉林大学学报(工学版).2005.03:277-281,300.

[4] 邓聚龙.累加生成灰指数律——灰色控制系统的优化信息处理问题[J].华中工学院学报.1987.05:7-12.

[5] 邓聚龙.本征性灰色系统的主要方法[J].系统工程理论与实践.1986.01.06:60-65.

[6] 倪啸枫,沈洪庆,李淑慧.车身外覆盖件面畸变缺陷影响因素[J]. 塑性工程学报.2013.03:48-54.

[7] 王金武,胡平,付争春,等.汽车覆盖件回弹试验及基于广义成形技术的回弹缺陷CAE分析方法[J].塑性工程学报.2010.01:41-45.

[8] 赵侠,李延奎,康成.汽车覆盖件常见质量问题及影响因素研究[J].热加工工艺.2010.15:185-187,190.

[9] 靳春梅,樊灵,邱阳,等.灰色理论在旋转机械故障诊断与预报中的应用[J].应用力学学报.2000.03:74-79,146.