基于原子晶体构型的高压固氩中的多体相互作用

郑兴荣， 付 云， 付文羽， 李向富， 李继弘

(1.陇东学院物理系， 庆阳 745000； 2. 贵州民族大学理学院， 贵阳 550025)

基于原子晶体构型的高压固氩中的多体相互作用

郑兴荣1， 付 云2， 付文羽1， 李向富1， 李继弘1

(1.陇东学院物理系， 庆阳 745000； 2. 贵州民族大学理学院， 贵阳 550025)

X射线衍射实验显示固氩是面心立方(fcc)晶格结构，目前对晶体氩的研究只限于两体，三体以及四体相互作用势. 本文利用多体展开方法和超分子单、双 (三)重激发耦合簇理论(CCSD(T))对固氩fcc晶格结构的三体和四体的几何构型、几何参数、不同体积下所有三体和四体构型的势能以及各构型所占比例等几个方面进行了准确的量子化学计算. 结果表明:所有三体构型中对总的三体势能贡献最大的是构型1、构型6、构型12和构型23；三体势及其交换部分和色散部分的计算结果与现有解析经验势在长程部分符合得非常好，但在短程部分有较小差异. 所有的四体构形中对总的四体势能贡献最大的是构型1，构型2，构型4，构型5，构型7和构型8；四体势及其交换势部分和色散部分的计算结果尚无解析经验势可比较.利用这些特殊构型的相关数据并结合其它构型，可拟合出更准确的三体经验势函数及其参数，也为拟合四体经验势函数及其参数提供了重要的参考价值.

固氩； fcc晶格结构； CCSD(T)； 三体势； 四体势

1 引 言

惰性元素具有球对称的满壳层电子结构，一般情况下很难与其他物质发生相互作用，但是在太阳、地球和其他行星内部的惰性元素均以高压状态存在[1,2]，且能够发生化学反应. 氩在实验上常用作静态高压实验的传压介质[3]，在理论上是用量子力学方法研究高压原子晶体结构的理想体系[4-6]. 人们利用金刚石对顶砧技术(DAC)测得了氩的物态方程，在室温下氩的最大压强已达到114 GPa，体积压缩比为3.06[7,8]. 常温低压下实验测得固氩是fcc晶格结构[7]. Aziz等人利用Hartree-Fock方法提出了Hartree-Fock Dispersion(HFD)-B[9,10], HFDID[11]以及Stawomir[12]等经验势，这些势函数能较好的描述两体相互作用,但当原子间距较小时与实验值有一定的差异. 随后Petr等人提出的两体势函数[13]能较准确地描述固氩的两体相互作用, 也能模拟出氩的多组实验数据及固氩的零温零压性质. Loubeyre[14,15]和Freiman[16]等人提出了氩的三体经验势函数，压强高于某一值时计算出的面心立方(fcc)氩的压缩线和结合能对应的理论压强值低于实验值；而当晶格体积小于某一值的高压区，由于三体势贡献过多的吸引效应，出现了氩的结合能随体积的减小而下降的不合理趋势. 因此，我们一方面有必要通过量子化学计算来检测该三体经验势的准确性，另一方面有必要探索更高阶多体相互作用在固氩中的贡献. 本文采用多体展开方法和超分子单、双 (三)重激发耦合簇理论(CCSD(T))方法和augmented correlation consistent quadruple zeta(aug-cc-pVQZ)基矢[17]计算了高压下固氩的fcc晶体中不同最近邻距离下任意三个原子间的三体构型和任意四个原子间的四体构型，对三体和四体的几何构型、几何参数、不同体积下所有三体和四体构型的势能以及各构型所占比例等几个方面对固氩的多体构型作了系统的分析. 由此得出不同最近邻距离下不同多体势的贡献程度，对于验证现有三体势函数的解析式以及参数的准确性和拟合四体势函数表达式可能具有比较重要的理论价值.

2 理论模型

固氩晶体中，任一原子被其不同邻近原子包围. 由于屏蔽效应，任一原子o对结合排斥势的贡献主要来自于o与周围近邻壳层(i=1,2,3,…)的有限的(n-1)个近邻原子的相互作用. 原子o和这(n-1)个原子构成一n原子的团簇Arn，该团簇的势能等于这n个原子从无穷远处移到当前位置处团簇总能量的变化

Vn(0,1,2,3,…,n-1)=E(r0,r1,r2,…,rn-1)-nE0,

(1)

其中E0代表孤立原子的基态能量，E(r0,r1,r2,…,rn-1) 代表n个原子处于r0,r1,r2,…,rn-1位置时团簇的基态总能量，它可以通过求解体系的薛定谔方程得到

φ=Eφ.

(2)

对于处在位置坐标r0和ri下的两氩原子o和i，它们所构成团簇的相互作用能，可用一个两体势描述

u2(o,i)=E(ro,ri)-2E0,

(3)

其中u2(o,i)代表两氩原子o，i间的两体相互作用，E(r0,ri)是两个氩原子分别位于r0，r0位置时它们所构成原子团簇Ar2的基态能量，E0代表一个孤立氩原子的基态能量. 当第三个氩原子j靠近这两个氩原子时，它们之间的的电子云分布彼此会发生变化，从而使得三个氩原子间存在三体相互作用，即三体势

u3(o,i,j)=E(ro,ri,rj)-3E0

-u2(o,i)-u2(o,j)-u2(i,j),

(4)

上式中E(r0,ri,rj)是三个氩原子分别位于r0,ri,rj位置时三个氩原子所构成团簇Ar3的基态能量. 同理，当第四个原子k接近这三个相互作用的原子时，三个原子之间的电子云分布会发生变化，从而使得四个氩原子间存在四体相互作用，即四体势

u4(o,i,j,k)=E(ro,ri,rj,rk)-4E0-[u3(o,i,j)+u3(o,i,k)+u3(o,j,k)+u3(i,j,k)]-[u2(o,i)+u2(o,j)+u2(o,k)+u2(i,j)+u2(i,k)+u2(j,k)]

(5)

同理，我们可以得到五体势，六体势……

在高压条件下，晶格中原子之间的距离减少.任一中心原子o与其近邻原子间的相互作用Vn可展开为原子o与(n-1)个近邻原子的两体式、三体势、四体势、五体势……之和，即

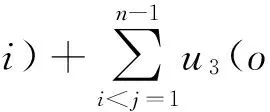
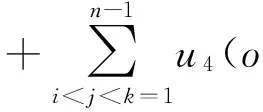
=U2(O)+U3(O)+U4(O)+…

(6)

其中U2(O)，U3(O)，U4(O)分别为中心原子o与近邻的(n-1)个原子中任意一个、两个、三个原子的两体，三体，四体相互作用，且U2(O)，U3(O)，U4(O)分别为各项对所有的近邻原子求和. 在实际求解过程中我们运用Gamess计算程序来求出氩原子团簇的多体势能，并运用CCSD(T)的从头计算方法和多体展开理论，对fcc固氩的性质作了研究.

3 结果与讨论

3.1 三原子构型的相互作用势能

3.1.1 Ar3三原子团簇的构型

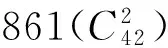
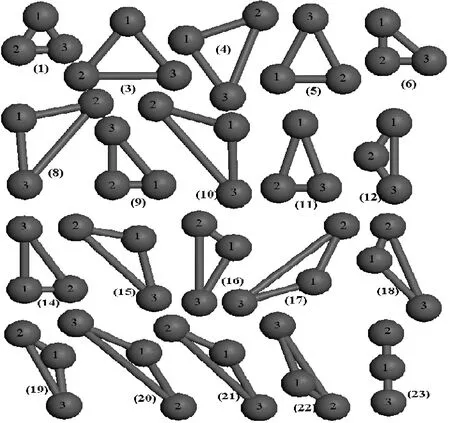
图1 fcc晶格中Ar3团簇的几何图形Fig. 1 Geometries of Ar3 clusters in fcc lattice

表1 fcc晶格中Ar3团簇的几何参数，θ1，θ2，θ3是三角形的三个内角(从小到大的顺序排列)，NP是三边长求和后的三分之一，NG表示权重因子

Table 1 Geometry parameters of Ar3clusters in fcc lattice,θ1，θ2，θ3are the three angles (in degree and the value from smallest to largest) of the triangle,NPis a third of the sum of three size lengths,NGrepresents the weight factor

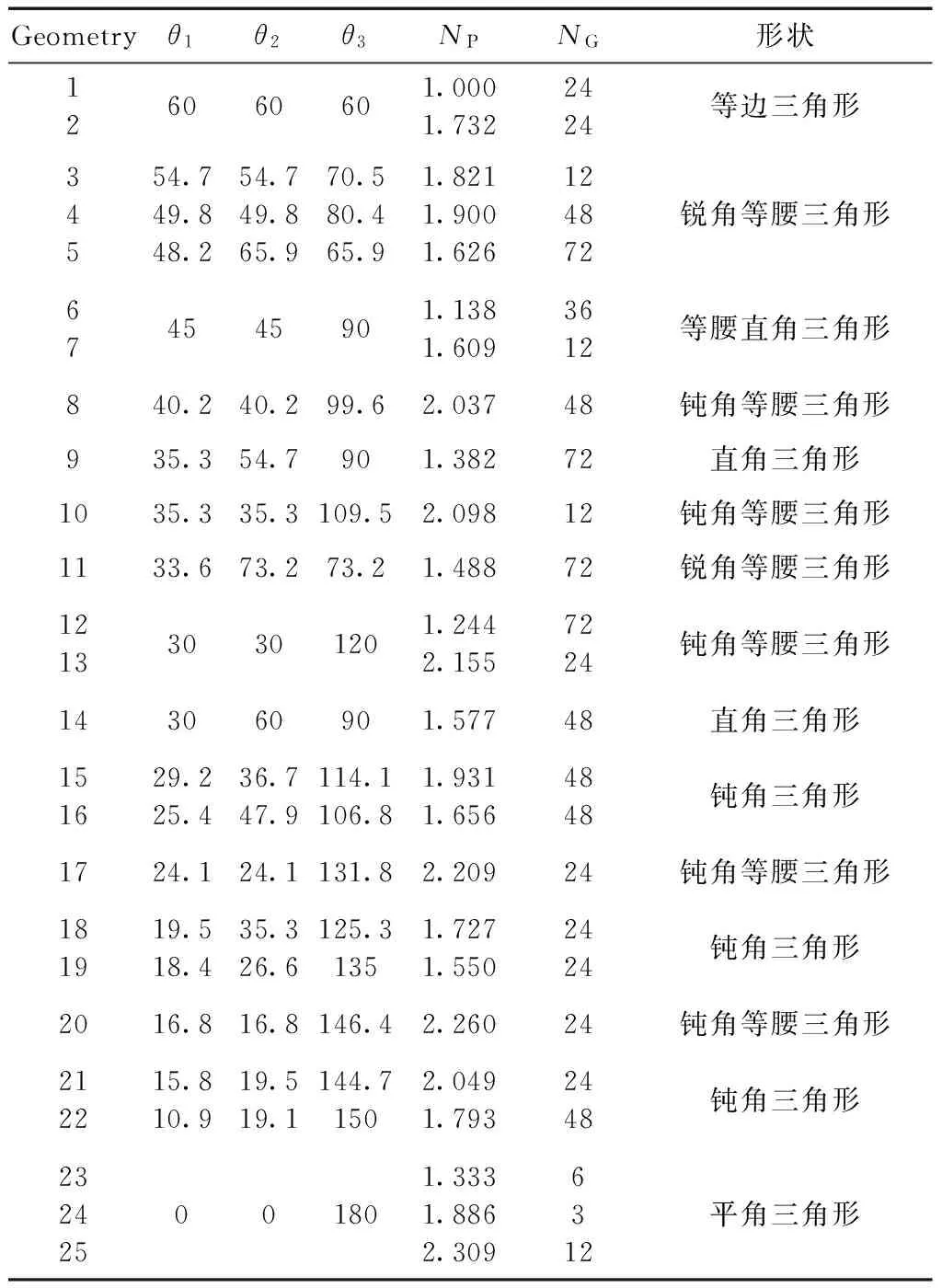
Geometryθ1θ2θ3NPNG形状126060601.0001.7322424等边三角形34554.749.848.254.749.865.970.580.465.91.8211.9001.626124872锐角等腰三角形674545901.1381.6093612等腰直角三角形840.240.299.62.03748钝角等腰三角形935.354.7901.38272直角三角形1035.335.3109.52.09812钝角等腰三角形1133.673.273.21.48872锐角等腰三角形121330301201.2442.1557224钝角等腰三角形143060901.57748直角三角形151629.225.436.747.9114.1106.81.9311.6564848钝角三角形1724.124.1131.82.20924钝角等腰三角形181919.518.435.326.6125.31351.7271.5502424钝角三角形2016.816.8146.42.26024钝角等腰三角形212215.810.919.519.1144.71502.0491.7932448钝角三角形232425001801.3331.8862.3096312平角三角形

3.1.2 不同体积下所有三体构型的能量

固氩的三体势构型共有25种，我们比较了这25种三原子构型在不同体积下三体势能所占的比例，如图2所示. 任何一组三原子构型的能量不仅与三体势φ3有关，还决定于相应的权重因子NG(见表1). 图2给出了体积分别为4.534 cm3/mol，10.385 cm3/mol，19.867 cm3/mol，27.253 cm3/mol时四种体积下所有三体构型下的能量相对大小，由图可以看出，在所有的构型中对总的三体势能贡献最大的是构型1、构型6、构型12和构型23. 构型1是一个权重因子为24的等边三角形，构型6是一个权重因子为36的等腰直角三角形，构型12是一个权重因子为72的锐角等腰三角形，构型23是一个权重因子为6的平角. 在体积较小时由于构型1的比例占据较大，所以其他几个重要的构型(构型6、构型12、构型23)在图中作用不太明显，但随着体积的增大，构型1的比例减小，这几个重要的构型也变得越来越重要. 因此，我们可以利用这几个构型结合其他所有构型的数值进行数据拟合.

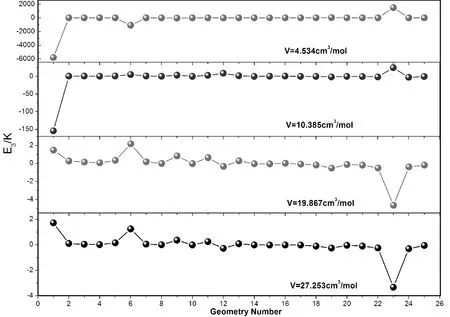
图2 不同体积下所有三体构型的三体势能Fig. 2 Potential energies of all three-body configurations at different volumes

3.1.3 氩三原子团簇的特殊构型的量子化学计算

由图2可知，固氩三原子的几个特殊构型--构型1(等边三角形，顶角θ=60°)，构型6(等腰直角三角形，顶角θ=90°)，构型12(钝角等腰三角形，顶角θ=120°)，构型23(平角θ=180°)在总的三体势能中所占比例很大，起到了重要作用. 因此，我们给出了由Pauli排斥效应引起的交换势部分U3S和长程色散势部分U3C(通常指Axilrod-Teller项，简称AT项)随三角构型的底边长度的变化关系，如图3所示.此外，与已有解析公式给出的交换势部分和色散势[14,16]部分进行了比较. 结果表明，本文理论计算结果与较早文献[16]有较大的偏差，但与经过修正后的理论结果[14]在长程色散部分和短程交换部分都有很好的一致性. 若以这几个特殊构型的相关数据为基础并结合其它构型，则可拟合出更准确的经验势函数及其参数.

3.2 四原子构型的相互作用势能

3.2.1 Ar4四原子团簇的构型

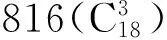
3.2.2 不同体积下所有四体构型的能量

由上面分析我们知道，四体势的构型共有28种，其中第8个构型有两种情况(如表2)，所以共有27种不同的构型，我们比较了这28种四原子构型在不同体积下四体势能中的比例，如图5所示. 任何一组四原子构型的能量不仅与φ4有关，还决定于相应的权重因子NG(见表2). 图5表明构型1到构型8非常重要，对四体势做出最大贡献的是权重因子为8的第一种构型，随着体积的增大它的贡献也在减少.

3.2.3 氩四原子团簇的特殊构型的量子化学计算

由上图5可以看出，前几个构型在所有构型中占的比例较大，起的作用较大，尤其是构型1(正四面体)，其次是构型2，构型4，构型5，构型7和构型8. 从两体势和三体势的理论计算与较早文献[13,14]比较可知，CCSD方法对于计算固氩的abintio数据具有较高的可靠性. 因此，在图6中给出了贡献较大的构型1，构型2，构型4和构型7的交换势部分U4S、色散势部分U4C以及二者之和四体势能U4的结果随最近原子间距R的变化关系，为拟合更准确的四体经验势函数及其参数提供了重要的参考价值.

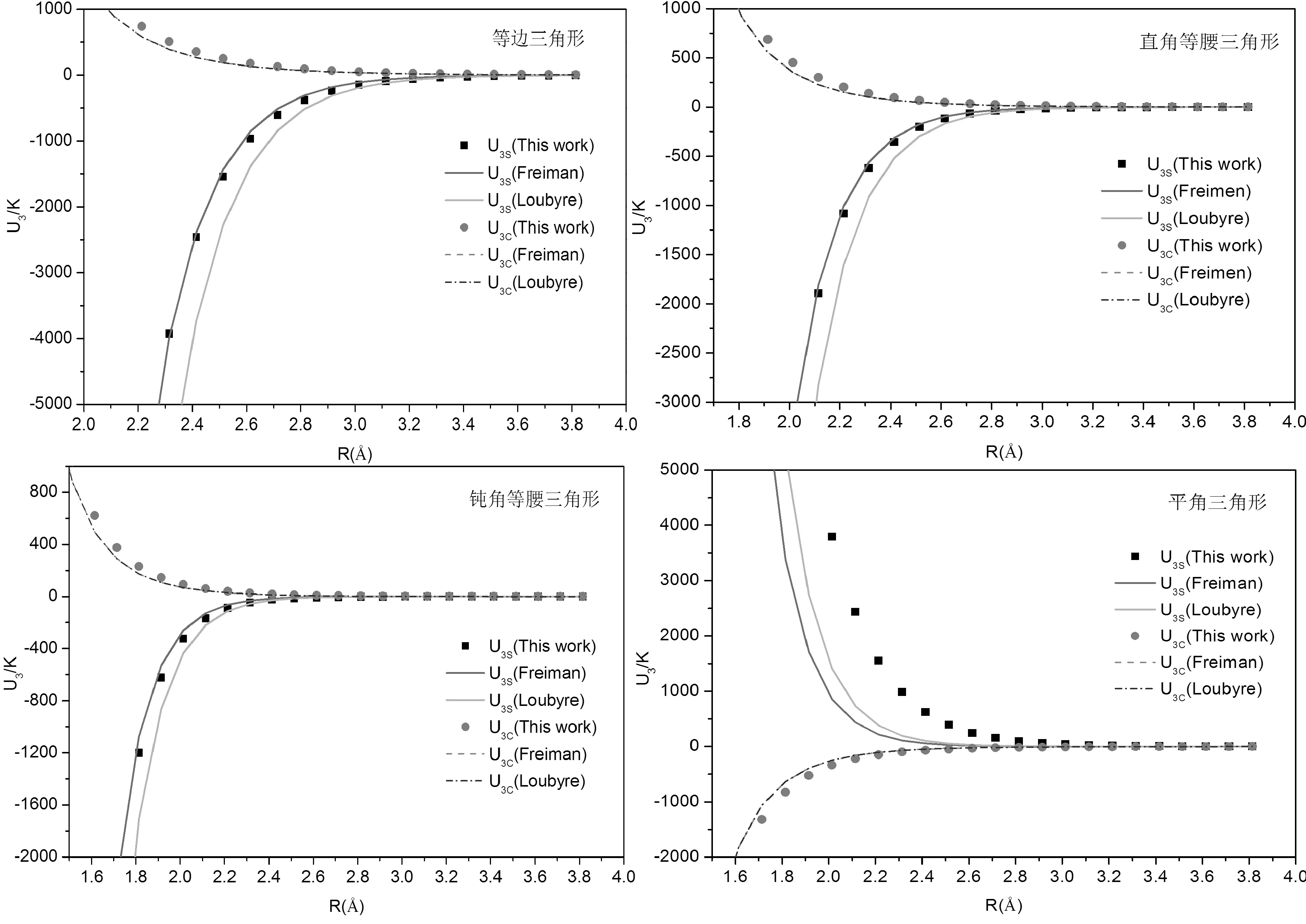
图3 氩三体势的CCSD(T)结果与经验三体势结果的比较Fig. 3 Comparison of CCSD results with the three-body experience potential results

表2 fcc晶格中Ar4团簇的几何参数.三边长r12、r13、r14以最近邻原子间距R为单位，θ213是r12、r13间的夹角，θ214是r12、r14的夹角，θ314是r13、r14的夹角，NG表示权重因子

Table 2 Geometry parameters of Ar4clusters in fcc lattice. The lengths of three edgesr12,r13,r14are in unit of the nearest interatomic distanceR,θ213is the angle betweenr12andr13,θ214is the angle betweenr12andr14,θ314is the angle betweenr13andr14,NGrepresents the weight factor

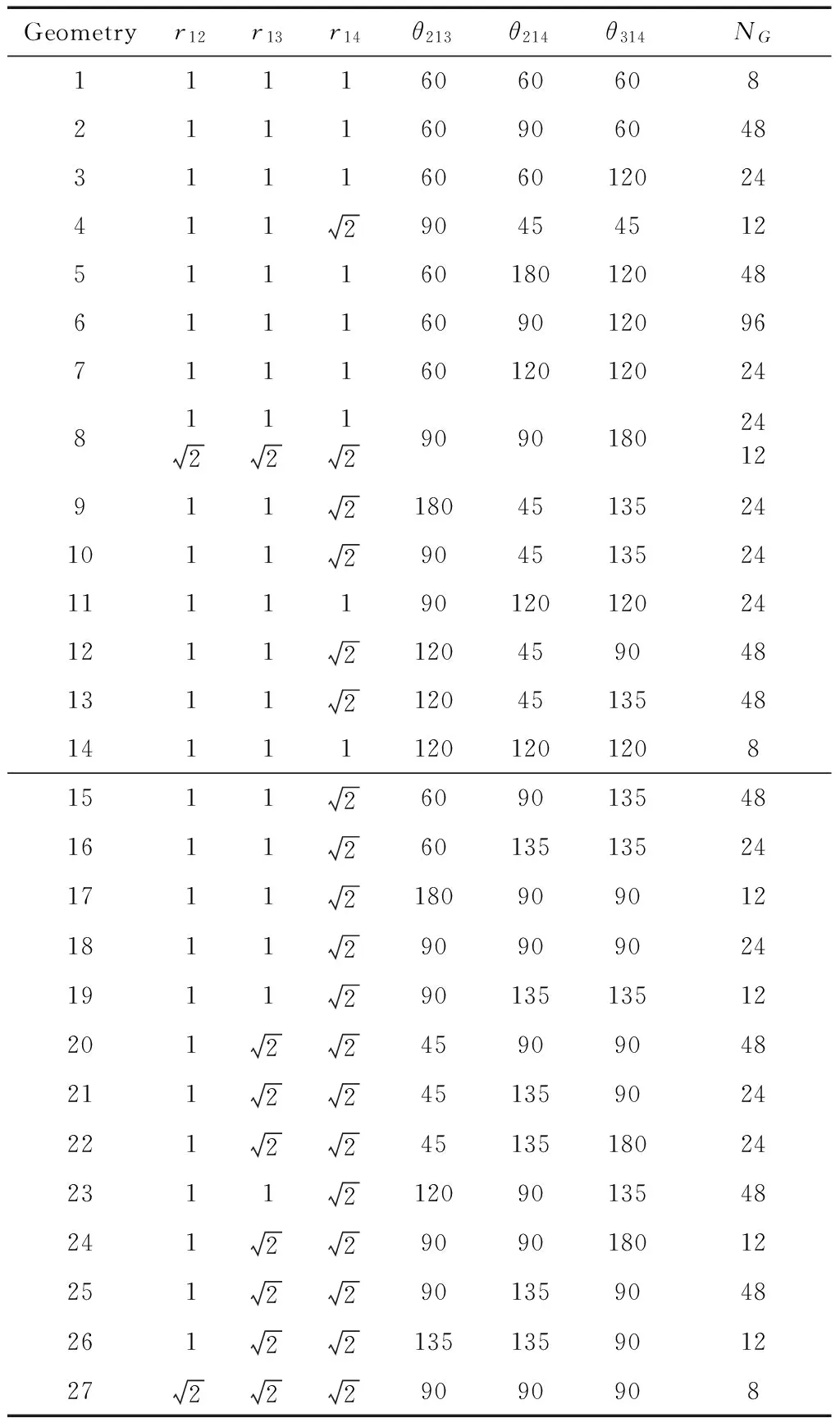
Geometryr12r13r14θ213θ214θ314NG11116060608211160906048311160601202441129045451251116018012048611160901209671116012012024812121290901802412911218045135241011290451352411111901201202412112120459048131121204513548141111201201208151126090135481611260135135241711218090901218112909090241911290135135122012245909048211224513590242212245135180242311212090135482412290901801225122901359048261221351359012272229090908

4 结 论

本文运用CCSD(T)的从头计算方法和多体展开理论，从不同最近邻壳层距离下任意三个原子间的三体构型和任意四个原子间的四体构型，对三体和四体的几何构型、几何参数、不同体积下所有三体和四体构型的能量以及各构型所占比例等几个方面对固氩fcc晶体的多体构型作了系统的分析. 通过计算，我们可以看出，所有25组三体构型中对总的三体势能贡献最大的是构型1、构型6、构型12和构型23；对三体势及其交换部分和色散部分进行了量子化学计算，计算结果与现有解析经验势在长程部分符合得非常好，但在短程部分有较小差异. 所有28组四体构形中对总的四体势能贡献最大的是构型1，构型2，构型4，构型5，构型7和构型8；对四体势及其交换势部分和色散部分也进行了量子化学计算，计算结果尚无解析经验势可比较. 若以这几个特殊构型的相关数据为基础并结合其它构型，可拟合出更准确的三体经验势函数及其参数，也为拟合四体经验势函数及其参数提供了重要的参考价值.

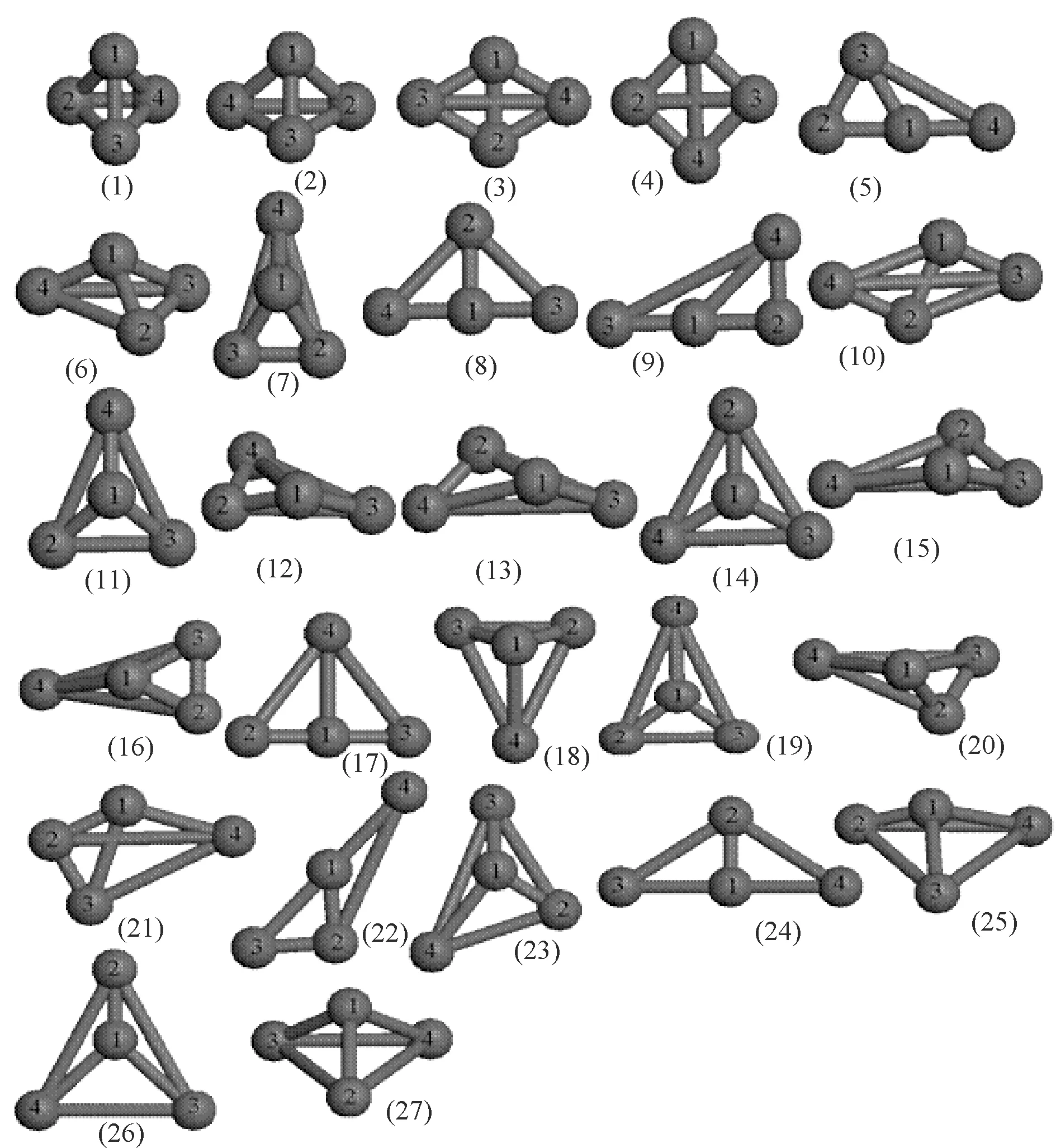
图4 fcc晶格中Ar4团簇的几何形状Fig. 4 Geometries of Ar4 clusters in fcc lattice

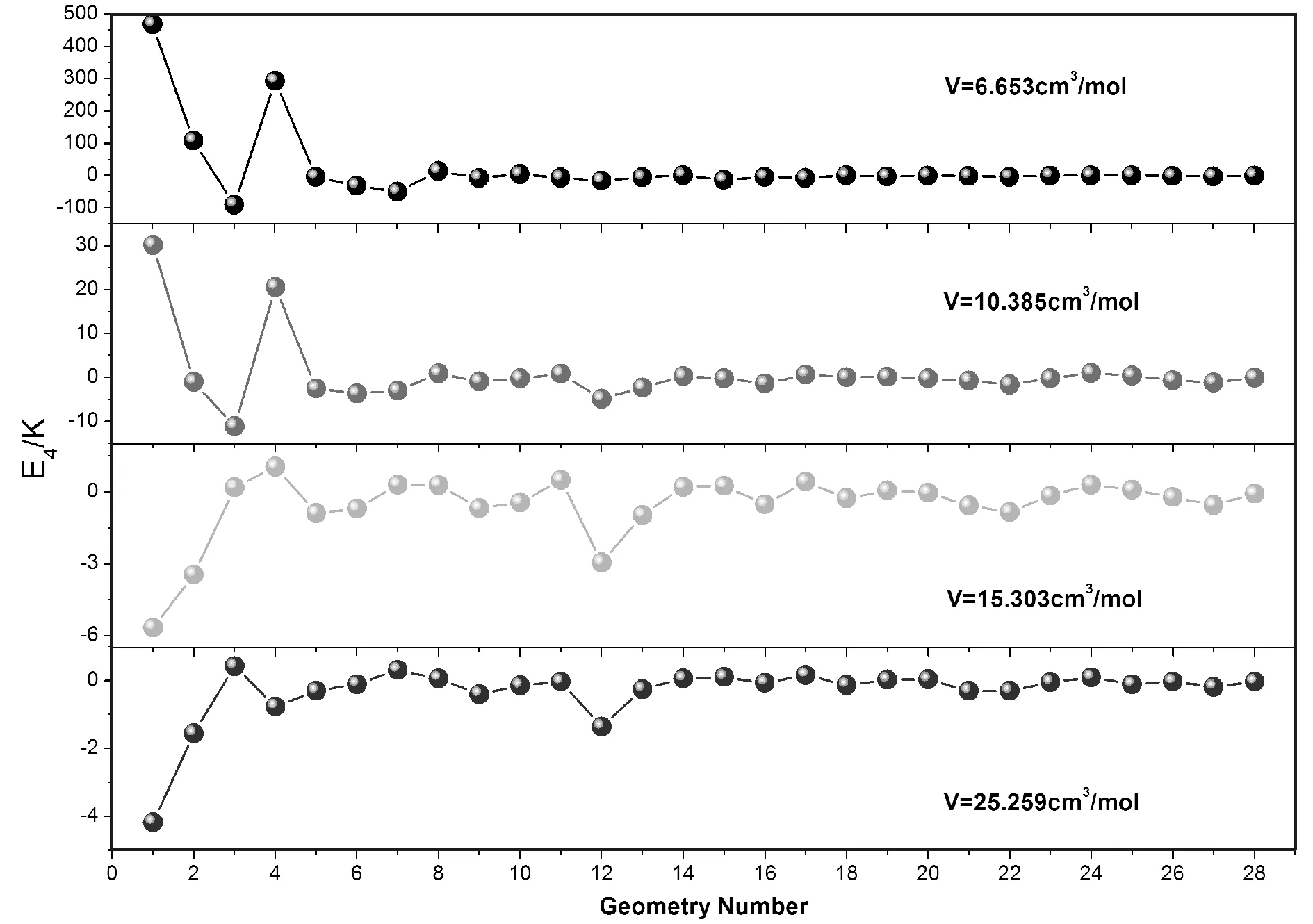
图5 不同体积下所有四体构型的势能Fig.5 Potential energies of all four-body potential configurations at different volumes

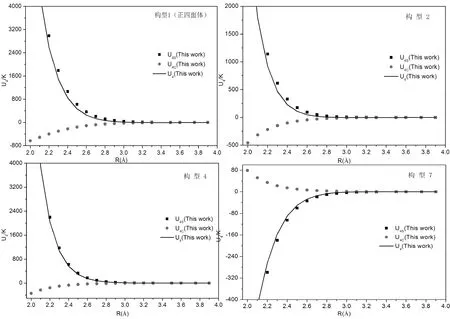
图6 固氩的四体势的量子化学计算Fig.6 Quantum chemistry calculation of four-body potential for solid argon

[1] Pepin R O. On the origin and early evolution of terrestrial planet atmospheres and meteoritic volatiles[J].Icarus, 1991, 92(2).

[2] Allegre C J, Hofmann A, Nions R O,etal. The argon constraints on mantle structure[J].Geophys.Res.Lett., 1996, 23: 3555.

[3] Mao H K, Xu J A, Bell P M,etal. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic condition[J].Geophys.Res., 1986, 91: 4673.

[4] Pechenik E, Kelson I, Makov G,etal. Many-body model of rare gases at high pressures[J].Phys.Rev. B, 2008, 78(13): 134109.

[5] Cazorla C, Errandonea D, Sola E,etal. High-pressure phases, vibrational properties, and electronic structure of Ne(He)2and Ar(He)2: A First-principles study[J].Phys.Rev. B, 2009, 80(6): 064105-1.

[6] Tse J S, Klug D D, Shpakov V，etal. High pressure elastic properties of solid argon from first-principles density functional and quasi-harmonic lattice dynamic calculations[J].SolidStateCommunications, 2002, 1098(02): 557.

[7] Errandonea D, Boehler R, Japel S,etal. Structural transformation of compressed solid Ar: An x-ray diffraction study to 114 GPa[J].Phys.Rev. B, 2006, 73(9): 092106.

[8] Ross M, Mao H K, Bell P M,etal. The equation of state of dense argon: a comparison of shock and static studies[J].J.Chem.Phys., 1986, 85: 1028.

[9] Aziz R A, Slaman M J. The argon and krypton interatomic potentials revisited[J].Mol.Phys., 1986, 58(4): 679.

[10] Aziz R A, Slaman M J. The repulsive wall of the Ar-Ar interatomic potential reexamined[J].J.Chem.Phys., 1990, 92(2): 1030.

[11] Aziz R A. A highly accurate interatomic potential for argon[J].J.Chem.Phys., 1993, 99: 4518.

[12] Cybulski S M, Toczylowski R R. Ground state potential energy curves for He2, Ne2, Ar2, He-He, He-Ar, and Ne-Ar: A coupled-cluster study[J].J.Chem.Phys., 1999, 111(23): 10520.

[13] Slavicek P, Kalus R, Paska P,etal., State-of-the-art correlated ab initio potential energy curves for heavy rare gas dimers: Ar2, Kr2, and Xe2[J].J.Chem.Phys., 2003, 119(4): 2101.

[14] Freiman Y A, Tretyak S M. Many-body interactions and high-pressure equations of state in rare-gas solids[J].LowTemperaturePhysics, 2007, 33(6-7):545.

[15] Loubeyre P. Three-body exchange interaction in dense helium[J].Phys.Rev.Lett., 1987, 58: 1857.

[16] Loubeyre P. Three-body-exchange interaction in dense rare gases[J].Phys.Rev. B, 1988, 37(10):5432.

[17] Angela K W, David E W, Kirk A P,etal. Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton[J].J.Chem.Phys., 1999, 110(16): 7667.

Many-body interaction of highly compressed solid argon based on atomic crystal configuration

ZHENG Xing-Rong1, FU Yun2, FU Wen-Yu1, LI Xiang-Fu1, LI Ji-Hong1

(1. Department of Physics, Longdong University, Qingyang 745000, China；2. College of Science, Guizhou Mizu University, Guiyang 550025, China)

X-ray diffraction experiments shows that solid argon is a face-centered cubic crystal structure (fcc structure). At present, crystal argon is studied involving two-, three- and four-body potentials. Using the many-body expansion method and the double cluster with full single and double excitations plus perturbative treatment of triples (CCSD(T)), the properties of fcc structure for solid argon which include geometrical configuration, geometrical parameters, potential energy of three- and four-body potentials and the proportion of all configurations at different volumes were accurately calculated. It is concluded that the configuration 1, 6, 12 and 23 play most important role in all three-body potential configurations. The calculation results of three-body potential, exchange potential and dispersion potential are in good agreement with the analytic experience potential in long-range part, but have small differences in short-range part. The configuration 1, 2, 4, 5, 7 and 8 play very important role in all four-body potential configurations, and there is not analytic experience potential to compare between the calculated results of four-body potential, exchange potential and dispersion potential. Using the data of these special configurations in combination with other configurations can fit a more accurate three-body experience potential function and its parameters, and also provide important reference value about fit four-body experience potential function and its parameters.

Solid argon; Face-centered cubic crystal structure; CCSD(T); Three-body potential; Four-body potential

2014-08-03

庆阳市自然科学基金(ZJ201306)

郑兴荣(1986—), 男，甘肃天水人，助教，主要从事材料计算研究.E-mail:zhengxingrong2006@163.com

103969/j.issn.1000-0364.2015.10.030

O641; O561.1

A

1000-0364(2015)05-0896-07