能谱涨落统计特征分析在Logistic混沌序列上的应用
肖 琴, 杨会杰
(1.上海理工大学管理学院, 上海 200090; 2.上海应用技术学院, 上海 201418)
能谱涨落统计特征分析在Logistic混沌序列上的应用
肖 琴1, 2, 杨会杰1
(1.上海理工大学管理学院, 上海 200090; 2.上海应用技术学院, 上海 201418)
混沌现象普遍存在于现实生活中, 混沌时间序列的分析是非线性系统研究的主要内容.基于Anderson 模型, 提出了一种新的混沌序列的分析方法. 通过对Logistic序列的分析, 使用能谱涨落分析方法, 发现能级斥力的大小能与最大Lyapunov指数相对应. 结果表明, 该方法能较好的预测混沌序列, 而且具有较强的抗噪声的能力, 不受初值敏感性的影响.
混沌序列; 随机矩阵理论; 能级间距
1 引 言
混沌系统是由确定性非线性系统产生的,是介于确定和随机之间的不规则运动. 随着混沌理论研究的不断深入的发展,混沌在很多的实际领域中得到了较为广泛的应用, 如生物医学、自动控制和通信等等.混沌时间序列的识别是混沌动力系统研究中的主要内容[1-4].
计算系统的Lyapunov指数是判断一个系统是否存在混沌的常见的研究方法. 计算最大Lyapunov指数常用的方法有Wolf算法[5]、小数据法[6,7]、矩阵算法[8]、混沌同步[9]等. 然而上述这些方法受时间序列的组成成分、初值、重构相空间等的影响非常大, 可能出现大的偏差, 计算过程又过于繁琐.
判断系统的混沌性质的还有频谱法[10,11]、非整数维法[12]、Kolmogorov熵[13]等等方法, 虽然她们都能判断系统的混沌性质, 然而不能把混沌的结构表明清楚, 实现起来困难, 不易操作. 对于界于混沌和周期分叉的系统容易出现误判. 因此, 寻求更加简单, 更能揭示混沌系统所蕴含的动力学性质的方法一直是备受关注的问题之一.
在本文中, 我们使用随机矩阵[14,15]的能级间距分布(NNS)分析方法[16-20], 通过把Logistic序列映射到Anderson 模型, 研究了对应的模型的能谱涨落统计特征, 从能谱的角度出发, 通过能谱的能级间距分布提取混沌的特性, 发现能较详细的说明混沌序列的结构. 这种方法具有普适性, 同样适用于其他的混沌序列. 该方法不受初值的影响.
2 方法与模型建立和求解
2.1 能级间距的Brody分布
随机矩阵理论表明: 哈密顿体系在完全规则(可积)的情况下, 它的能级间隔分布(NNS)为Poisson分布. 而混沌体系对应的量子系统,它的NNS分布为Wigner分布. 大量的物理体系是这两极限情形的“混合共存”. Brody分布可用于描述这种情况下能级间隔统计的性质. 其形式为,
fB(s)=β(α+1)sαexp(-βsα+1),
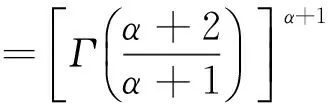
(1)
α为能级斥力参数,α=0和1时, 上述分布函数分布蜕变为Poisson和Wigner分布函数. Poisson和Wigner分布函数为:
fp(s)=exp(-s)
fw(s)=(πs)exp(-πs2)
(2)
2.2 模型的建立
我们把时间序列映射到一维无序格子, 时间序列的大小作为能量的大小, 由Anderson模型得到哈密顿矩阵, 通过分析格子的哈密顿矩阵的能级间隔特征来度量时间序列的结构特征.
我们首先对时间序列进行归一化, 对于任一个序列X1,X2,X3,…,Xn, 取
,i=1,2,…,N
(3)
取xmax=max(x1,x2,…xn), 我们得到了新的序列y1,y2,…yn, 其中,yi=xi-xmax.
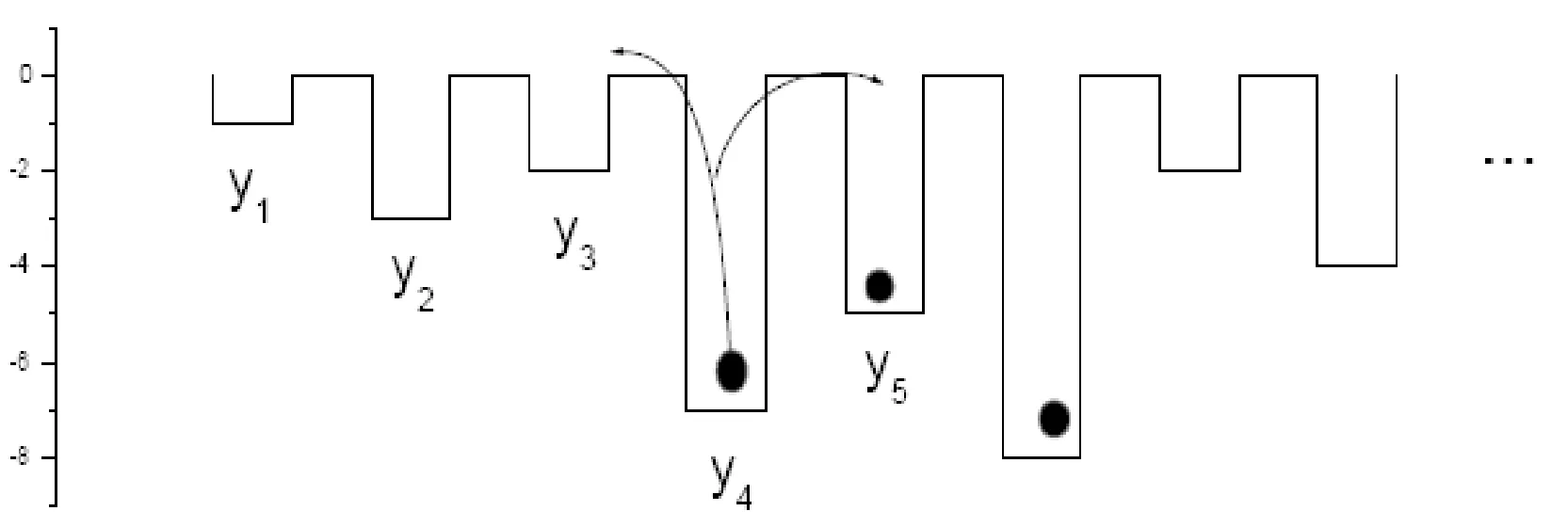
图1 新的序列对应于Anderson模型里的能量的无序变化 Fig. 1 Time series corresponding to the disordered energy of the Anderson model
然后我们把新的序列对应于一维格点的点能量, 这样就得到了一个Anderson模型. 它的哈密顿量可写为:
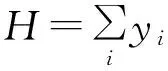
(4)
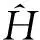
{ΔEk|k=1,2,…,N-1}
={E2-E1,E3-E2,…,EN-EN-1}
(5)
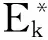
3 Logistic混沌序列仿真实验
3.1Logistic方程
我们以Logistic映射作为混沌的典型例子,来探索混沌序列的结构性质.
Logistic方程: Xn+1=λXn(1-Xn)
0≤Xn≤1,0<λ≤4.
(6)
对于Logistic映射序列, 我们知道: 当λ≥3.57时进入混沌状态, 在实验中我们取3.57≤λ≤4, 来考察随着λ的增大, 序列由倍周期分叉变成混沌状态的反复变化过程. 我们先以0.3为初值, 随着的λ不同大小,产生不同Logistic映射序列. 在实验中, 我们为了使实验不是由特殊情况产生的, 我们每次都做了20次以上的实验, 并且每次实验的序列取10000-100000不等的长度大小.
对于离散Logistic映射序列来说, 序列的最大Lyapunov指数表征序列沿着轨迹的平均发散张开程度, 即对初始条件的敏感依赖性. 在不同的状态下, 最大Lyapunov指数可能大于、等于或小于零. 如果最大Lyapunov指数大于零, 表示运动轨道在每个局部都不稳定, 相邻轨道指数分离, 形成混沌吸引子. 指数越大, 相邻轨道指数分离越快, 长期的预测性越不可能, 因此正的Lyapunov可作为混沌行为的判据. 如果指数小于零, 表明每次迭代后轨道的差距越来越小, 对应于各个周期的运动状态. 指数由负变正, 表明周期轨道向混沌的转变.其中λ=3.63,3.74,3.83,3.84,3.9等点时, 最大Lyapunov指数为负值, 这里我们称之为奇异点. 很显然, 奇异点处的性质会显著不同于其他的混沌的点.
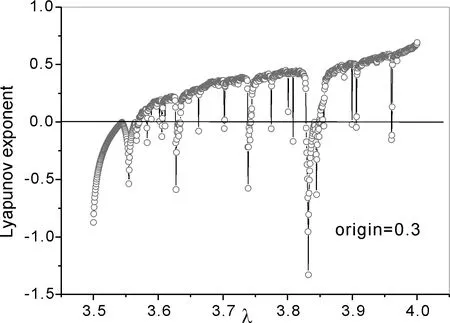
图2 初值为0.3的Logistic映射序列的最大Lyapunov指数变化图, 其中3.57≤λ≤4(以0.005为划分间隔)Fig. 2 The largest Lyapunov exponent of the Logistic series with the initial value 0.3(in 0.005 divided interval)
3.2 实验结果
3.2.1 初值相同, 序列的长度不同
我们先选取具有相同的初值, 而序列的长度不同的Logistic映射序列做多次的实验,分别计算它们的能级间隔分布的能级斥力α的分布的情况. 我们发现结果与序列的长度无关, 都能得到基本一样的结果.
对不同的Logistic映射序列, 图3中我们取3.5≤λ≤4计算得到的能级间隔分布所对应的能级斥力参数α, 结合Lyapunov指数图可以看出,α的变化趋势与Lyapunov指数几乎相同, 甚至更为细微.
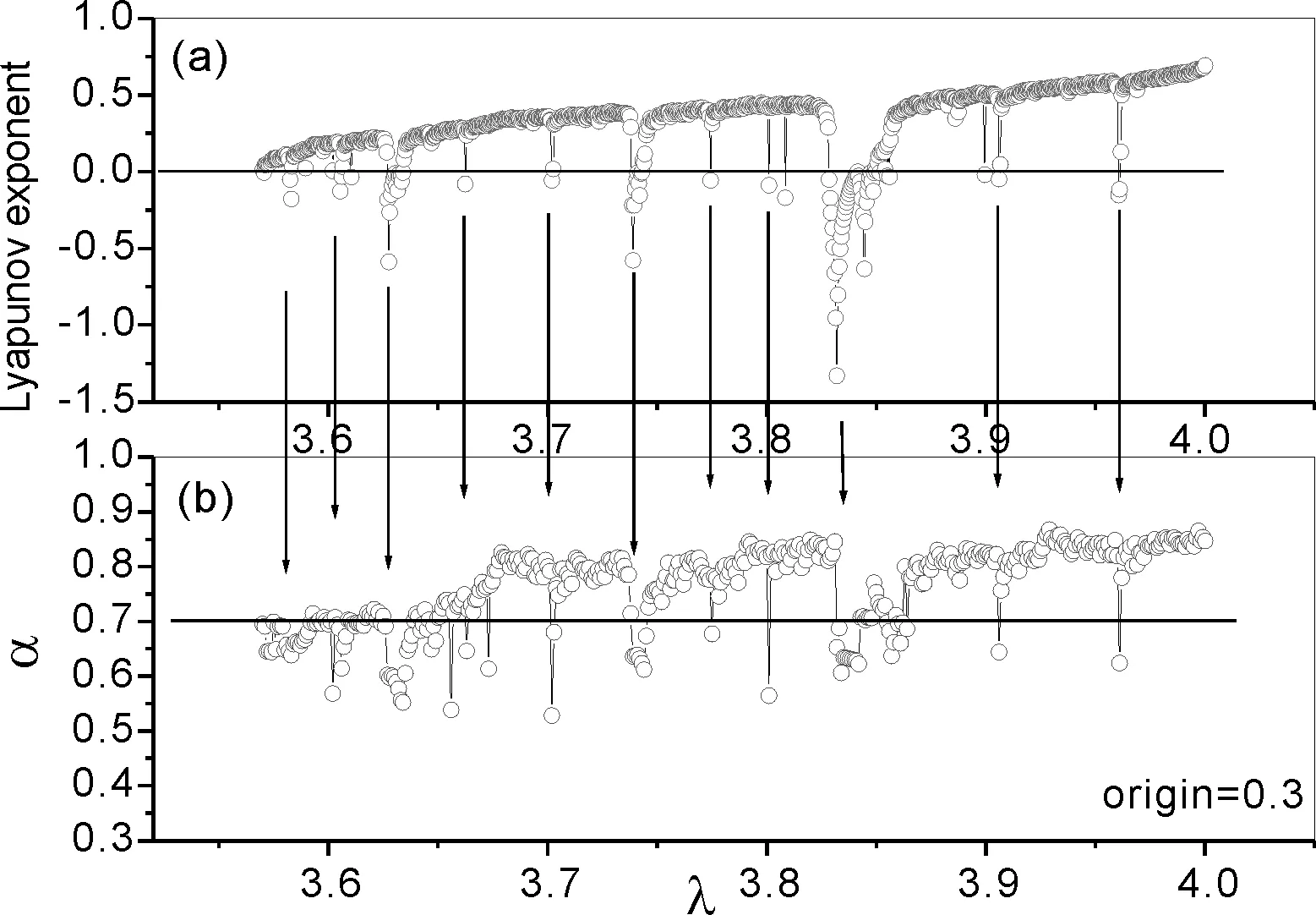
图3 初值为0.3的Logistic序列最大Lyapunov指数与相同初值的Logistic序列的能级间隔分布的能级斥力α值的对应图 Fig. 3 The largest Lyapunov exponent of Logistic series (a) and the corresponding graph of the series NNS level repulsion α (b) with the origin value 0.3
当λ大于3.57后, 与Lyapunov指数相同的是, 在它的奇异点处能级间距参数也会有突然骤降, 我们从图3中可以看出, α值以临界值0.7为界, 越接近1越近于Wigner分布, 也说明了当系统处于完全混沌状态时, 能级间隔关联性较强. 因此可以说明, 系统能级间隔的关联性可以反映系统的混沌程度, 关联性越强, 混沌程度越强.
3.2.2 初值不同的序列
对于序列具有不同的初值而具有相同的跳跃能的情况, 我们也进行了分析. 我们得到了相同的结论, 如图4可知, 初值的不同并不影响能级斥力α与最大Lyapunov指数的对应关系. 从图像中可以看出, 跳跃能一样而初值不一样, 则我们得到的临界α值相同, 都是0.7.
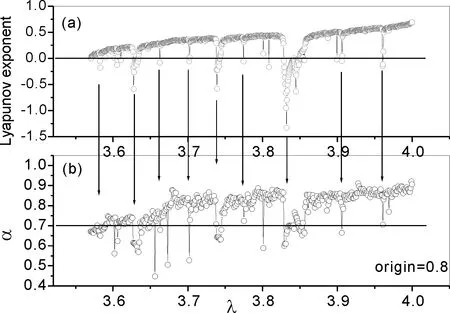
图4 初值为0.8的Logistic序列最大Lyapunov指数与相同初值的Logistic序列的能级间隔分布的能级斥力α值的对应图Fig. 4 The largest Lyapunov exponent of Logistic series (a) and the corresponding graph of the series NNS level repulsion α (b) with the origin value 0.8
3.2.3 具有不同跳跃能的序列
我们进一步进行分析, 对于具有不同的初值的Logistic映射序列, 我们同样也计算了Lyapunov指数与系数α的关系, 我们得到了相同的结论, 同样也有相同的对应关系. 我们发现, 对于不同的跳跃能, 所对应的NNS的能级斥力系数临界值α值的高度不同, 而与最大Lyapunov指数的对应关系没有改变. 如图5所示, 在实验中我们取跳跃能为τ=31/2, 得到对应的临界α值为0.8.
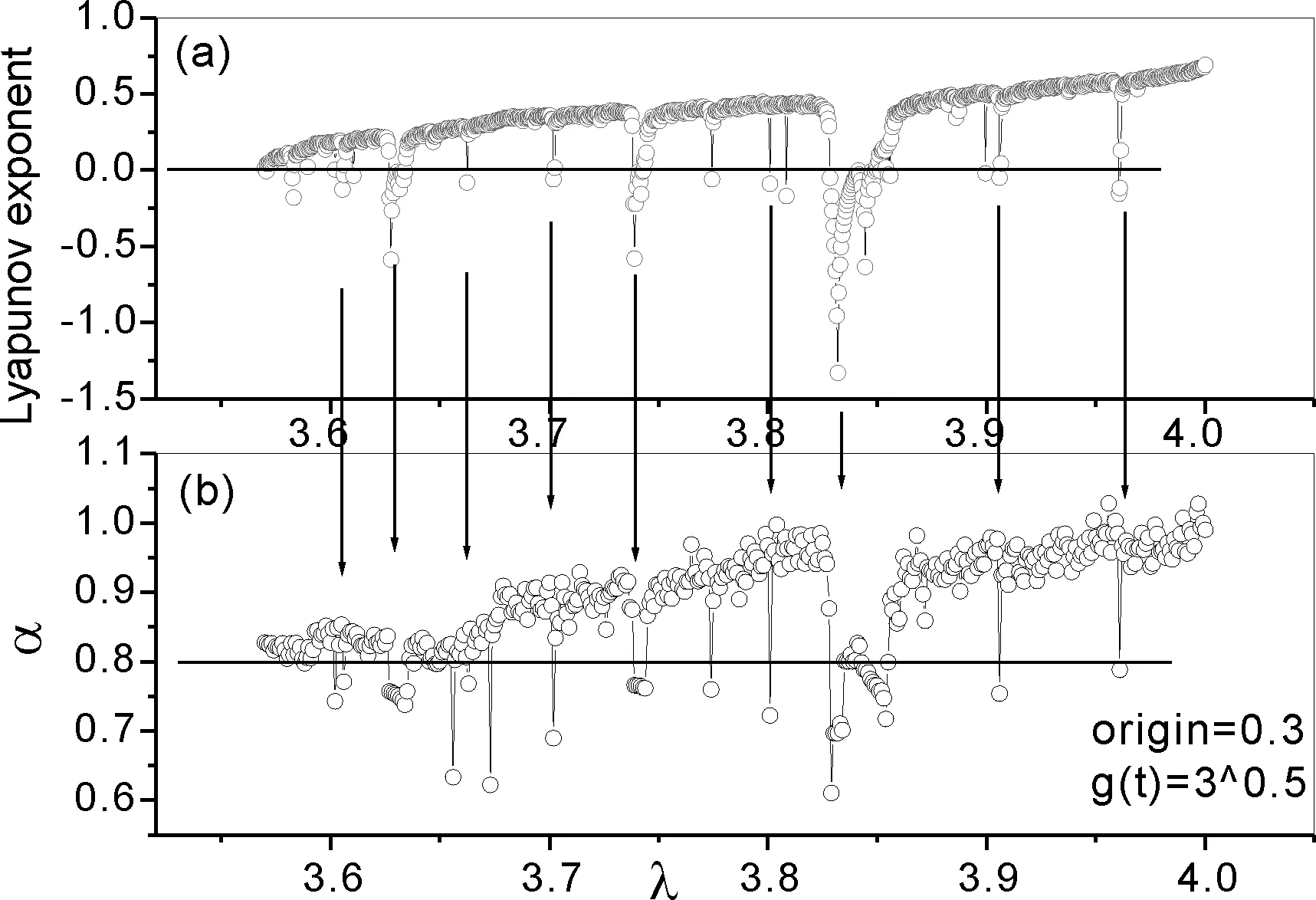
图5 初值为0.3的Logistic序列最大Lyapunov指数与跳跃能为τ=31/2的Logistic序列的能级间隔分布的能级斥力α值的对应图Fig. 5 The largest Lyapunov exponent of Logistic series (a) and the corresponding graph of the series NNS level repulsion α (b) with the τ=31/2 jump energy worth
3.2.4Lorenz序列的实验结果
混沌序列Lorenz序列的方程为:
dx(1,1)=10*(x(2)-x(1));
dx(2,1)=x(1)*(30-x(3))-x(2);(7)
dx(3,1)=x(1)*x(2)-8/3*x(3);
我们也取同样的方法进行实验, 在实验中取跳跃能为1, 我们得到了以下的一些NNS的能级斥力α值为表1中的数据, 从数据中可以看出, 他们都要远远大于临界值0.7, 可以判断为混沌系统. 另外, 能级斥力α值接近1, 因此为Winger分布. 对于混沌序列Lorenz序列其他的参数的情况, 我们有相同的结论.

表1 混沌序列Lorenz序列的能级斥力α值
4 结 论
本文从随机矩阵理论出发, 推导出了与最大Lyapunov指数相对应的识别混沌序列的新的方法. 我们运用Anderson模型, 把Logistic序列大小对应于能量的大小, 进而得到了相应的哈密顿矩阵, 在使用随机矩阵的能级间隔涨落的统计分布, 得到了能与Lyapunov指数对应的斥力参数. 对于不同的跳跃能, 临界的NNS的能级斥力参数α不同. 对于有不同的初值, 而跳跃能一样的情况, 这个临界值不变. 结果表明, 本文算法对初值不敏感, 因此是一种有效简单的方法, 对于我们对序列的性质的分析和探究有一定的作用.
[1]XuG,ZhangYD,ZhangXX, et al.Digitalimageencryptionalgorithmbasedonanalternatingiterativechaoticsystem[J].Journal of University of Science and Technology of Beijing, 2012, 34(4): 464(inChinese)[徐刚, 张亚东, 张新祥, 等. 基于交替迭代混沌系统的图像加密算法[J]. 北京科技大学学报, 2012, 34(4): 464]
[2]LiAP,LiuGR,ShenXQ.Synchronizationofuncertainfractional-orderchaoticsystemusingfractional-ordersystemwithdifferentorderandparametersidentification[J]. Computer Engineering and Applications, 2013, 49(4): 245(inChinese)[李安平, 刘国荣, 沈细群. 不同阶分数阶混沌系统的同步与参数辨识[J]. 计算机工程与应用, 2013, 49(4): 245]
[3]GaoXW,TianDZ,LiK.Time-delaypredictionmethodbasedonmaximumLyapunovexponentandElmanneuralnetwork[J]. Science China, 2013, 43(8): 1042(inChinese)[高宪文, 田中大, 李锟. 基于lyapunov-Elman的网络控制系统时延预测方法[J]. 中国科学(信息科学), 2013, 43(8): 1042]
[4]YaoTL,LiuHF,XuJL, et al.Noise-levelestimationofnoisychaotictimeseriesbasedontheinvariantofthelargestLyapunovexponent[J]. Acta Phys. Sin., 2012, 61: 610503(inChinese)[姚天亮,刘海峰,许建良, 等. 基于最大lyapunov指数不变性的混沌时间序列噪声水平估计[J]. 物理学报, 2012, 610503]
[5]AlanW,SwiftJB,SwinneyHI, et al.DeterminingLyapunovexponentsfromatimeseries[J]. Phys.D, 1985, 16: 285.
[6]RosensteinMT,CotlinsJJ,DeJucaCJ.ApracticalmethodsforcalculatinglargestLyapunovexponentsfromsmalldatasets[J]. Phys.D, 1993, 65: 117.
[7]XiangXD,GuoYH.CalculatinglargestLyapunovexponentofchaotictimeseries[J]. Forecasting, 2001, 5: 76(inChinese)[向小东, 郭耀煌.混沌时间序列最大Lyapunov指数的计算[J]. 预测, 2001, 5: 76]
[8]WuZB.Remarkonmetricanalysisofreconstructeddynamicsfromchaotictimeseries[J]. Phys.D, 1995, 85: 485.
[9]AndrzejS.EstimationofthelargestLyapunovexponentinsystemswithimpacts[J]. Chaos Solitons and Fractals, 2000, 11: 2443.
[10]ShiL,YangF,LiHS.Researchontestingmethodofphase-noisebasedondirectspectrumanalysismethod[J]. Aerospace Shanghai, 2012, 3: 69(inChinese)[施柳, 杨芳, 李海松. 基于直接频谱法的相位噪声测试方法研究[J]. 上海航天, 2012, 3: 69]
[11]XuCY,DingK,LinHB, et al.Noiseinfluenceonamplitudeandphaseestimationaccuracybyinterpolationmethodfordiscretespectrum[J]. Journal of Vibration Engineering, 2011, 6: 633(inChinese)[徐传燕, 丁康, 林慧斌. 离散频谱分析比值较正法幅值和相位的抗噪声分析[J]. 振动工程学报, 2011, 6: 633]
[12]Wayland,BromleyD,PickcttD.Recognizingdeterminismsinatimeseries[J]. Phys. Rev. Lett., 1993, 70(5): 580.
[13]LaiYC,LernerD.Effectivescalingregimeforcomputingthecorrelationdimensionforchaotictimeseries[J]. Phys.D, 1998, 115: 1.
[13]QiLY. Random matrix spectral analysis on complex network[D].Tianjing:NankaiUniversity, 2004(inChinese)[齐龙瑜. 复杂网络的随机矩阵谱分析[D]. 天津: 南开大学, 2004]
[14]JiangZB,YangHJ,WangJB.Complexitiesofhumanpromotersequence[J]. Phys.A, 2009, 388: 1299.
[15]ZhuGM,YangHJ,YangR, et al.Uncoveringevolutionaryagesofnodesincomplexnetworks[J]. The European Physical JournalB, 2012, 85: 106.
[16]TaoCY,LuoJL,LiZR, et al.Statisticsoffluctuationsinvibrating-energyspectraoftriatomicmolecules[J]. Journal of Atomic and Molecular Physics, 1994, 11(4): 360(inChinese)[陶长元, 罗久里, 李泽荣, 等. 三原子分子体系振动能谱的涨落统计特征[J]. 原子与分子物理学报, 1994, 11(4): 360]
[17]CaselleM,MagneaU.Randommatrixtheoryandsymmetricspace[J]. Phys. Rep., 2004, 394: 41.
[18]XinHL,MundyJA,LiuZ, et al.Atomic-resolutionspectroscopicimagingofensemblesofNanocatalystparticlesacrossthelifeofafuelcell[J]. Nano Letters, 2012, 12: 490.
[19]KravtsovVE,OssipovA,YevtushenkoOM, et al.Returnprobabilityandscalingexponentsinthecriticalrandommatrixensemble[J]. Journal of PhysicsA: Mathematical and Theoretical, 2011, 44(30): 5003.
[20]BogomolnyE,GiraudO.EigenfunctionentropyandspectralcompressibilityforcriticalRandommatrixensembles[J]. Phys. Rev. Lett., 2011, 106: 101.
Spectral analysis approach to chaotic series
XIAO Qin1, 2, YANG Hui-Jie1
(1.Business School, University of Shanghai for Science and Technology, Shanghai 200093, China;2.College of Science, Shanghai Institute Technology, Shanghai 201418, China)
Chaos is ubiquitous in real life. Identification of chaotic time series is the main content of nonlinear field. We map a time series to a 1-dimensional random lattice. By using random matrix theory, we find that the statistical characteristics of level spacing are consistent very well with the Lyapunov exponent behaviors. The results show that the method has strong anti-noise ability and non-initial-state-sensitivity.
Chaotic time series; Random matrix theory; Nearest neighbor level spacing
上海市重点学科建设项目(XTKX2012);国家自然科学基金项目(10975099,10635040);上海市教委创新基金(13YZ072);上海高校特聘教授 (东方学者)岗位计划
肖琴(1976—),女,汉,博士研究生. E-mail: sunshao3000@163.com
103969/j.issn.1000-0364.2015.10.029
N941
A
1000-0364(2015)05-0891-05
投稿日期:2014-03-04

