拉曼效应对低双折射光纤的偏振态演化分析

张思远 , 贾维国, 王玉平, 王美洁, 门克内木乐

(1. 内蒙古大学物理科学与技术学院, 呼和浩特 010021; 2. 内蒙古广播电视大学教务处， 呼和浩特 010010)

拉曼效应对低双折射光纤的偏振态演化分析

张思远1, 贾维国1, 王玉平2, 王美洁1, 门克内木乐1

(1. 内蒙古大学物理科学与技术学院, 呼和浩特 010021; 2. 内蒙古广播电视大学教务处， 呼和浩特 010010)

在准连续情况下, 通过求解低双折射光纤中含有拉曼效应的右旋与左旋圆偏振光所满足的耦合非线性薛定谔方程, 得到了归一化功率以及相位差的解析解. 利用解析解，推导出了椭圆率和方位角的表达式, 研究了拉曼效应和传输距离对偏振态演化的影响, 并用相平面法对椭圆率和方位角随着输入功率的变化进行了直观描述. 结果表明: 低双折射光纤在传输的过程中, 拉曼效应和传输距离都是影响其偏振态稳定性的因素, 均改变了椭圆率和方位角的演变周期以及振荡幅度.

低双折射光纤; 拉曼效应; 偏振态; 椭圆率; 输入功率

1 引 言

在某些通信以及非通信领域中, 我们希望光纤在传输的过程中, 偏振态能够保持稳定.正是基于这样的需求人们研发出了偏振保持光纤[1], 低双折射光纤[2-5]正是其中使用较多的一种偏振保持光纤, 所以相比较普通光纤, 低双折射光纤在传输时具有良好的保偏特性.此外其相位差非常小, 而且和光纤的长度没有线性的关系. 因此在光纤传感器[6-9], 光纤电流互感器, 光纤激光器[10]以及相关的光通信领域中有着广泛的应用. 相信在未来的相关通信领域和传感技术中, 低双折射光纤必定会起到更大的作用, 这就要求其输出端的偏振光必须保持稳定.

然而低双折射光纤在传输时, 随着输入功率的增加, 势必会产生一系列新的非线性效应, 如：光波和光学声子发生相互作用产生拉曼效应. 拉曼效应的产生会造成光纤的偏振态无法保持稳定性, 一旦光纤的偏振态不稳定, 将会带来很多麻烦. 不稳定的偏振态不仅使信号幅度产生变化, 还会造成信号的波形失真, 严重时甚至损伤光通信的通信质量及信号的可靠度. 现今国内外讨论光纤的偏振不稳定性的文章已经非常多, 但鲜有将拉曼效应这一非线性因素考虑在内的偏振不稳定性的文章, 所以考虑拉曼效应下的偏振不稳定性还有待进一步的探究, 因此研究拉曼效应对光纤的偏振态演化具有重要的现实意义.

表述光的偏振态的方法有很多, 例如: 斯托克斯参量法[11]，庞加莱球法[12], 矩阵法[13]等. 本文从准连续情况下, 利用低双折射光纤中, 含有拉曼效应的右旋与左旋圆偏振光所满足的耦合非线性薛定谔方程出发, 得到了归一化功率以及相位差的解析解, 利用解析解, 推导出了椭圆率和方位角的表达式, 研究了拉曼效应以及传输距离对低双折射光纤偏振演化的影响, 并用相平面法进行了直观描述.

2 理 论

准连续情况下, 低双折射光纤中, 含有拉曼效应的右旋与左旋圆偏振光所满足的非线性耦合薛定谔方程为[14]:

(1)

(2)

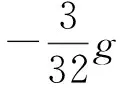
(3)

(4)

其中：p+和p-为归一化功率, φ+和φ-为相位. 对(3)式求导, 并利用欧拉公式化简得:

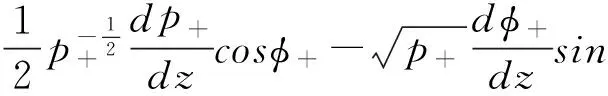
(5)

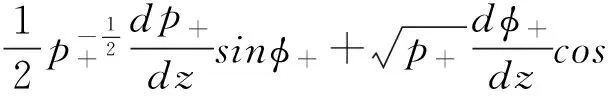
(6)

(5)式乘以 , (6)式乘以 , 将两式相加得:

(7)

整理化简得到:

(8)

式中：Ψ=φ+-φ-为相位差. 同理可以得到:

(9)

(10)

上述(8)、(9)、(10)三个方程描述的是归一化功率p+,p-, 相位差Ψ与光纤的传输距离z之间的关系. 在这三个方程中, 有两个沿着光纤保持为常量的量:

p=p++p-

(11)

(12)

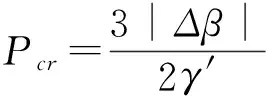
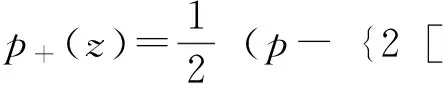
(13)

其中：cn(z|m)是雅克比椭圆函数，宗量z为：

(14)

(15)

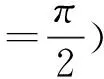
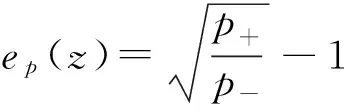
(16)

将(13)式和(14)式代入(16)式, 得到:

(17)

由(15)式得到方位角的表达式为:

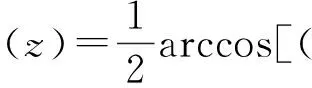
(18)

得到椭圆率和方位角的表达式后, 再结合解析解, 我们就可以将偏振态的演化用轨迹的形式在椭圆率-方位角相空间内表示出来.

3 结果分析与讨论

3.1 不考虑拉曼效应时，偏振态的演化轨迹

随着输入功率的不断增加, 非线性效应导致依赖强度的相位在两个耦合模之间发生改变, 因此将会引起偏振椭圆的非线性旋转, 相平面轨迹的变化如图1所示. 其中：输入功率p=10 W , 非线性系数γ=44.9 W-1/km , 传播常数差Δβ=1.256 m-1. 椭圆率ep=0表示线偏振态和各角度的方位角; 椭圆率ep=1和椭圆率ep=-1分别表示右旋圆偏振态和左旋圆偏振态.

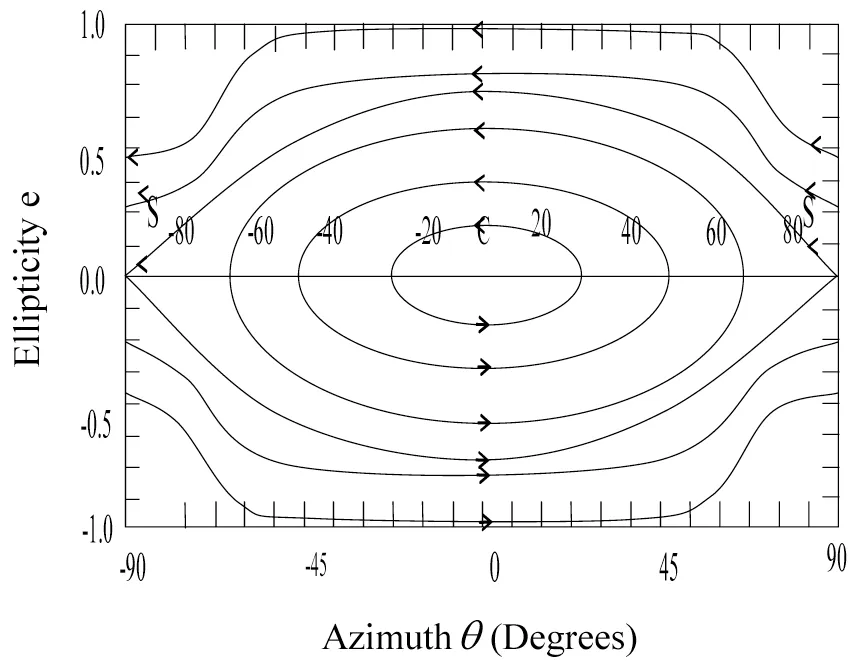
图 1 偏振态演化的相空间轨迹Fig.1 Phase-space trajectory representing evolution of the polarization state

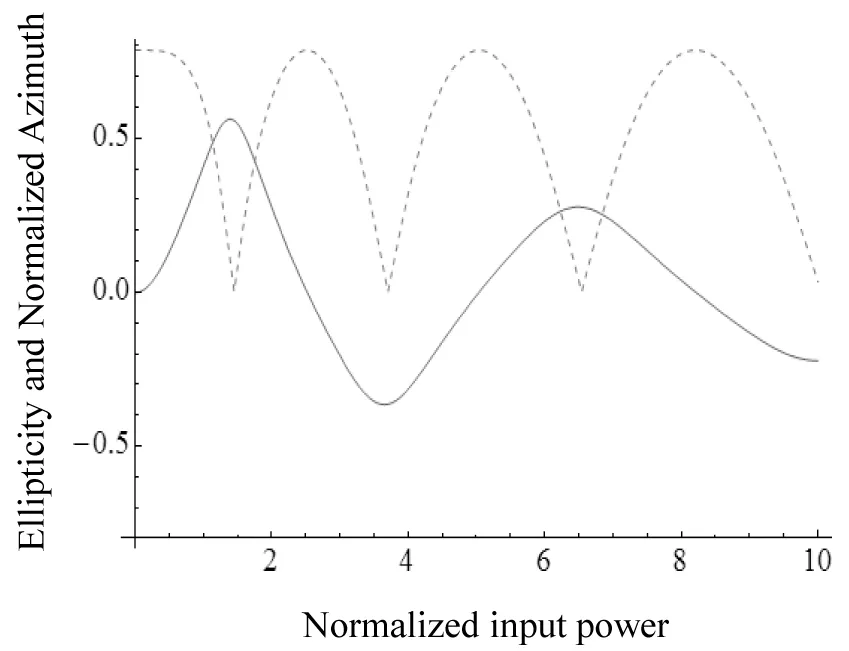
图2 椭圆率和归一化方位角与归一化输入功率的变化关系Fig.2 The relationship between ellipticity(solid curve)and normalized azimuth angle with normalized input power

图3 当输入功率p=10时，椭圆率和归一化方位角与归一化传输距离的变化关系Fig.3 The relationship between ellipticity(solid curve)and normalized azimuth angle with normalized transmission distance when input power is 10

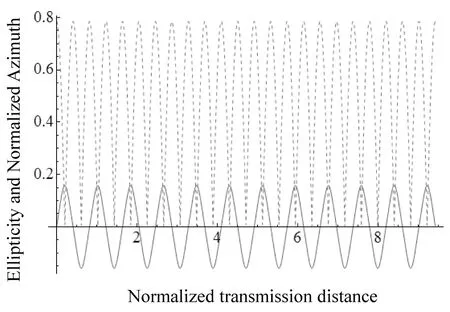
图4 当输入功率p=20时，椭圆率和归一化方位角与归一化传输距离的变化关系Fig.4 The relationship between ellipticity(solid curve)and normalized azimuth angle with normalized transmission distance when input power is 20

从图1可以看出: 一条分界线将相空间分为两个不同的区域, 在θ=0和ep=0附近(光靠近慢轴方向偏振)的区域, 其偏振态演化的轨迹都是闭合的, 且所有的轨道距离都等于各自的拍长, 闭合的轨道表示振荡运动, 说明慢轴处于稳定的中心; 在方位角θ=90°与θ=-90°附近(光靠近快轴方向偏振)的区域, 分界线将相空间分割成了振荡运动区域(闭合的轨迹)和旋转运动区域; 例如: 一束线偏振光在方位角θ=60°输入, 将会在慢轴方向做振荡运动, 于此同时在椭圆率ep=0.5处做完整的旋转运动. 这是由于在快轴方向对应不稳定的马鞍点S, 因此即使输入偏振态只发生了极微小的变化, 也会在输出端引起很大的变化. 图2表示在方位角θ=45°, 传输距离z=3.14时, 椭圆率随归一化输入功率的变化关系(其中实线表示椭圆率), 虚线表示方位角随归一化输入功率的变化关系. 在图2中, 输入功率是从低输入功率一直变化到高输入功率的. 当处于低功率时, 此时没有非线性效应; 随着输入功率的增大, 产生了非线性效应, 影响了偏振态的演变周期, 使其变大. 所以由于电子非线性的作用, 椭圆率和方位角的周期均随着输入功率的增加而变大, 椭圆率的峰值逐渐变小, 而方位角的峰值没有发生变化. 当输出偏振态为线偏振态(ep=0), 输入方位角θ=45°时, 依次经过右旋椭圆偏振态, 线偏振态, 左旋椭圆偏振态, 最终在方位角θ=-45°时, 再次回到线偏振态; 表明偏振态的演变在任意角度的方位角传输时依次经过线偏振态, 右旋椭圆偏振态, 线偏振态, 左旋椭圆偏振态, 最终又回到线偏振态. 图3, 图4是在其余条件不变, 输入功率分别为p=10和p=20时, 椭圆率和归一化方位角随归一化输入功率的变化关系. 图3、图4的输入功率直接从高输入功率开始取值, 它受到电子非线性效应的影响. 从图3可以看出: 在整个传输距离内, 椭圆率和方位角的周期均保持稳定, 峰值也没有发生改变, 振荡幅度相同. 相比较图3, 当输入功率增大到p=20时, 从图4可以看出: 此时椭圆率和方位角的振荡周期变小, 椭圆率的峰值降低, 但方位角的峰值没有改变.表明低双折射光纤在传输时, 增大输入功率时, 偏振态演变的周期变小, 且椭圆率的峰值降低, 但方位角的峰值保持稳定.

3.2 考虑拉曼效应时，偏振态的演化轨迹

图5是在输入功率p=10 W, 非线性系数γ=44.9 W-1/km, 传播常数差Δβ=1.256 m-1, 方位角θ=-45°, 传输距离z=3.14时, 考虑拉曼效应, 且平行拉曼增益g″(Ω)=0.5时, 椭圆率随归一化输入功率的变化关系. 图6是在其余条件不变, 考虑拉曼效应, 且平行拉曼增益为g″(Ω)=1时, 椭圆率随归一化输入功率的变化关系. 图7和图8分别是在其余条件不变, 考虑拉曼效应, 且平行拉曼增益g″(Ω)=0.5, 传输距离z=6.28与平行拉曼增益g″(Ω)=1, 传输距离z=6.28时, 椭圆率随归一化输入功率的变化关系.

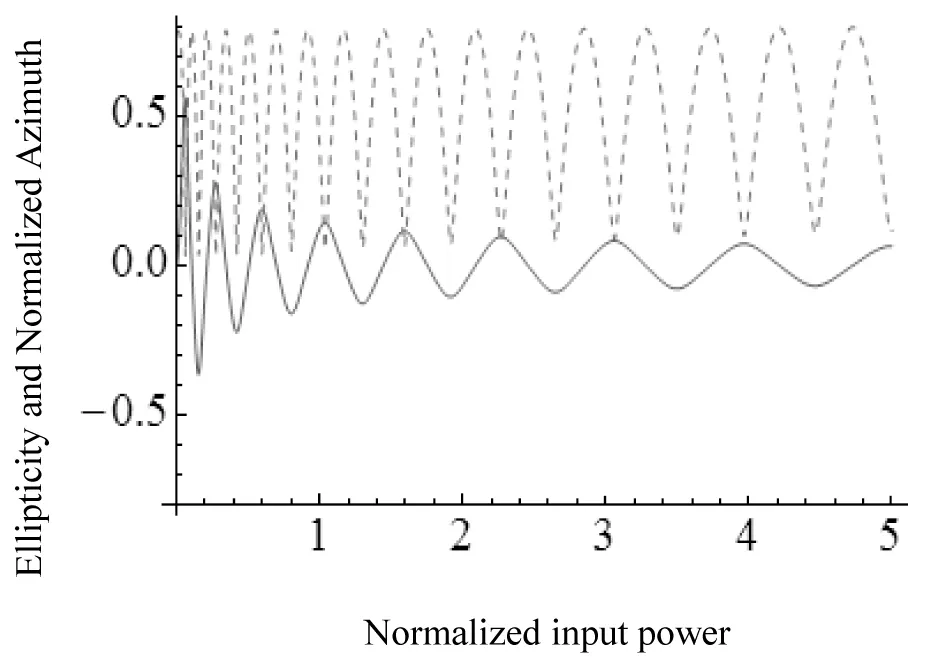
图 5 平行拉曼增益g″(Ω)=0.5时，椭圆率和归一化方位角与归一化输入功率的变化关系Fig.5 The relationship between ellipticity(solid curve)and normalized azimuth angle with normalized input power when the parallel Raman gain is 0.5

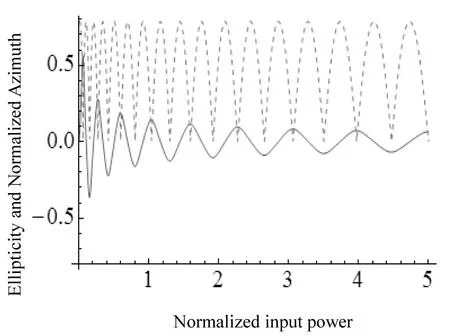
图 6 平行拉曼增益g″(Ω)=1时，椭圆率和归一化方位角与归一化输入功率的变化关系Fig.6 The relationship between ellipticity(solid curve)and normalized azimuth angle with normalized input power when the parallel Raman gain is 1

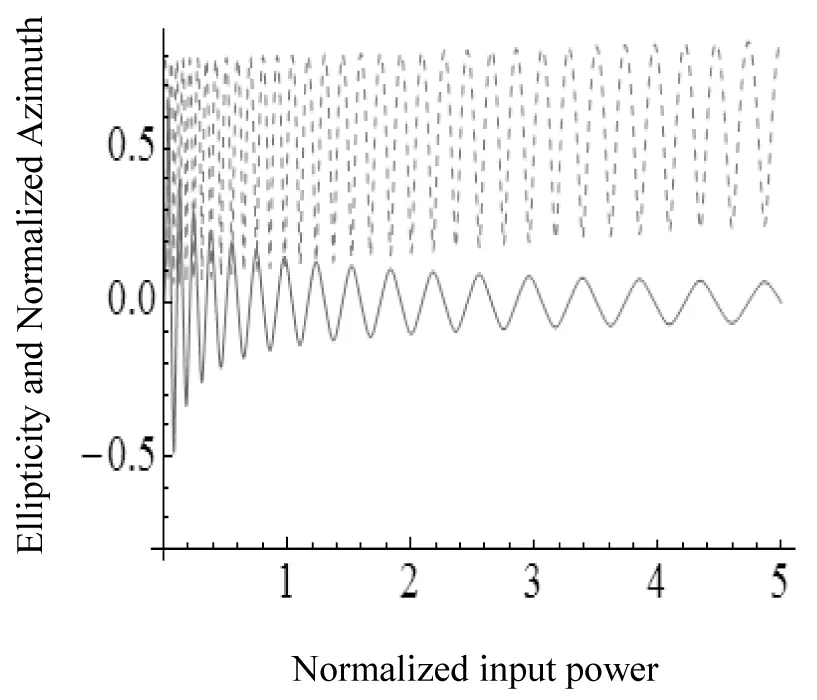
图 7 平行拉曼增益g″(Ω)=0.5，传输距离z=6.28时，椭圆率和归一化方位角与归一化输入功率的变化关系Fig.7 The relationship between ellipticity(solid curve)and normalized azimuth angle with normalized input power when the parallel Raman gain is 0.5 and the normalized transmission distance is 6.28

图 8 平行拉曼增益g″(Ω)=1，传输距离z=6.28时，椭圆率和归一化方位角与归一化输入功率的变化关系Fig.8 The relationship between ellipticity(solid curve)and normalized azimuth angle with normalized input power when the parallel Raman gain is 1 and the normalized transmission distance is 6.28

从图5可以看出: 当考虑拉曼效应后, 随着输入功率的增加, 光纤的偏振态依然是呈周期性变化的. 相比较图2, 椭圆率和方位角演变的周期随着输入功率的增加而变小, 且振幅不断衰减; 但是随着输入功率增大到一定程度时, 二者演变的周期趋于稳定, 不再变化, 并且峰值之间的间距相当, 振荡幅度也趋于稳定, 不再衰减. 从图6可以看出: 当逐渐增大平行拉曼增益, 椭圆率和方位角和图5相比, 并无太明显的变化. 表明在低双折射光纤传输的过程中, 当考虑拉曼效应后, 随着输入功率的增加, 确实改变了椭圆率和方位角演变的周期以及振荡幅度; 但是当进一步增大拉曼效应, 拉曼效应对二者的演变周期和振荡幅度的影响降低, 没有明显的改变. 相比较图5和图6, 从图7和图8可以看出: 随着传输距离的增大, 在功率较低的时候, 椭圆率和方位角的周期发生了明显的改变, 急剧变小, 椭圆率的振荡衰减幅度较大, 而方位角的振荡幅度则基本保持稳定; 随着输入功率逐渐增强, 椭圆率和方位角的周期和峰值变化幅度降低, 振荡衰减的幅度较小, 直到趋于稳定. 表明在光波传输的过程中, 拉曼效应和传输距离都是影响偏振态稳定性的因素, 均改变椭圆率和方位角的演变周期以及其振荡幅度.

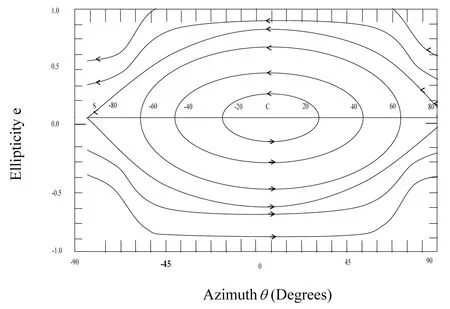
图9 考虑拉曼效应时，偏振态演化的相空间轨迹Fig.9 Considering the Raman effect，phase-space trajectory representing evolution of the polarization state

图9为输入功率p=10 W, 非线性系数γ=44.9 W-1/km, 传播常数差Δβ=1.256 m-1, 考虑拉曼效应后, 取g″(Ω)=1时, 偏振态演化的相空间轨迹. 相比较图1的情形, 从图9我们可以看出: 考虑拉曼效应后, 沿着慢轴方向的稳定中心不再位于方位角θ=0°, 拉曼效应使得偏振椭圆的稳定中心处的方位角变大, 同时增大了偏振椭圆的椭圆率. 其椭圆率越高, 使得低双折射光纤中光的偏振态越接近于线偏振态, 此时拉曼效应不再改变光传输时的偏振态. 同时, 整个相空间轨迹向上平移, 并且向右发生了平移, 使得光偏振态演化的周期变小. 表明考虑拉曼效应后，拉曼效应改变了光波偏振态演变的稳定中心, 且减小了偏振态演变的周期.

4 结 论

光波在低双折射光纤中传输时, 随着输入功率的增加, 产生拉曼效应, 拉曼效应会改变光波偏振态演变的稳定中心与周期. 当不考虑拉曼效应, 且方位角θ=45°, 传输距离z=3.14时, 随着输入功率的增加, 光纤的偏振态是呈周期性变化的. 偏振态演变的周期随着输入功率的增加而变大, 且振幅不断衰减; 当保持输入功率一定, 增大传输距离时, 椭圆率的变化是周期性的, 其周期和峰值均逐渐变小, 但方位角的峰值没有变化, 振荡保持稳定; 当考虑拉曼效应, 且平行拉曼增益为g″(Ω)=0.5时, 随着输入功率的增加, 光纤的偏振态依然是呈周期性变化的. 相比较不考虑拉曼效应的情形, 椭圆率和方位角的周期开始随着输入功率的增加而变小, 椭圆率的振幅不断衰减, 而方位角的振幅基本保持稳定; 随着输入功率增大到一定程度时, 二者演变的周期趋于稳定, 不再变化, 并且峰值之间的间距相当, 振荡幅度也趋于稳定, 不再衰减; 当进一步增大拉曼效应, 拉曼效应对偏振态的演变周期和振荡幅度的影响降低, 没有明显的改变; 在考虑拉曼效应的基础上, 逐渐增大传输距离, 在功率较低的时候, 椭圆率的周期和峰值发生了明显的改变, 急剧变小, 且振荡衰减幅度较大; 而方位角的周期和振荡幅度没有太大的改变; 随着输入功率逐渐增强, 椭圆率的周期和峰值变化幅度降低, 振荡衰减的幅度较小, 直到趋于稳定. 表明在光波在低双折射光纤传输的过程中, 拉曼效应和传输距离都是影响其偏振态稳定性的因素, 均改变了椭圆率和方位角的演变周期以及振荡幅度.

[1] Agrawal G P.NonlinearFiberOptics(2ndEd.) [M]. Boston: Academic Press, 2008.

[2] Murdoch S G, Leonhardt R, Harvey J D. Polarization modulation instability in weekly birefringent fibers [J].OpticsLetters, 1995, 20(8): 866.

[3] Yin J Q, Jia W G, Wang X Y,etal. Gain of single-mode birefringence fiber[J].JournalofAtomicandMolecularPhysics, 2011, 28(4): 321(in Chinese) [尹建全, 贾维国, 王旭颖, 等. 单模双折射光纤中的增益[J]. 原子与分子物理学报, 2011, 28(4): 321]

[4] Yin J Q, Jia W G, Wang X Y,etal. Gain of stoker in birefringence fiber[J].JournalofAtomicandMolecularPhysics, 2011, 28(11): 1089(in Chinese) [尹建全, 贾维国, 王旭颖, 等. 双折射光纤中斯托克斯波的增益谱[J]. 原子与分子物理学报, 2011, 28(11): 1089]

[5] Wang J P, Su Y, Li Y Q. Evolution of output light SOP in pulsed magnetic field sensor based-on Faraday effect [J].JournalofBeijingUniversityofPostsandTelecommunication, 2007, 30(5): 58(in Chinese) [王江平, 苏洋, 李玉权. Faraday效应的磁场传感器光偏振态的演化[J]. 北京邮电大学学报, 2007, 30(5): 58]

[6] Wang J F, Jin Y X, Yu Z,etal. Refractive index sensor based on all-fiber multimode interference[J].InternationalJournalforLightandElectronOptics, 2013, 124 (14): 1845.

[7] Wang Z P, Wang Y K, Sun S. Effect of modulation error on all optical fiber current transformers [J].JournalofSensorTechnology, 2012, 02 (04): 172.

[8] Chai H Y, Jia W G, Han F,etal. Raman effect on gain spectrum of different frequency propagation regimes in photonic crystal fibers[J].ActaOpticaSinaca, 2013, 33(12): 1219001.1(in Chinese)[柴宏宇, 贾维国, 韩凤, 等. 光子晶体光纤不同频率区域拉曼效应增益谱[J]. 光学学报, 2013, 33(12): 1219001.1]

[9] Wang X Y, Jia W G, Yin J Q,etal. Parametric amplification and Raman scattering in photonic crystal fibers [J].ActaOpticaSinaca, 2011, 31(6): 0606001.1(in Chinese) [王旭颖, 贾维国, 尹建全, 等. 光子晶体光纤中的参量放大与拉曼散射[J]. 光学学报, 2011, 31(6): 0606001.1]

[10] Jia W G, Qiao L R, Yang J,etal. Influence of high-order dispersion on gain spectrum in high-birefringence fiber [J].HighPowerLaserandParticleBeams, 2012, 24(12): 2791(in Chinese) [贾维国 ,乔丽荣, 杨军, 等. 高阶色散对高双折射光纤增益谱的影响[J]. 强激光与粒子束, 2012, 24(12): 2791]

[11] Wang M J, Jia W G, Zhang S Y,etal. Raman effecting on the state of polarization evolution in a low-birefringence fiber[J].ActaPhys.Sin., 2014, 63 (10): 141(in Chinese)[王美洁, 贾维国, 张思远, 等. 拉曼效应对低双折射光纤偏振特性的影响[J].物理学报, 2014, 63 (10): 141]

[12] Tong L G, Jia W G, Yang J,etal. Polarization stability analysis of nonlinear coherent coupling by using Poincare sphere in a weekly birefringence fiber[J].InfraredandLaserEngineering, 2012, 41 (11): 2967.

[13] Feldman S F, Weinberger D A, Winful H G. Polarization instability in a twisted birefringence optical fiber [J].OpticalSocietyofAmerican, 1993, 10(7): 1191.

[14] Han F, Jia W G, Chai H Y,etal. Raman effect on gain spectrum in law-birefringence fiber[J].ActaOpticaSinaca, 2013, 33(7): 0729002.1(in Chinese) [韩凤, 贾维国, 柴宏宇, 等. 低双折射光纤中拉曼效应对增益谱的影响[J]. 光学学报, 2013, 33(7): 0729002.1]

[15] Lin Q, Agrawal G P. Raman response function for silica fibers[J].OptLett., 2006, 31(21): 3086.

[16] Winful H G. Polarization instabilities in birefringent nonlinear media: application to fiber-optic devices [J] .Opt.Lett., 1986, 33 (11): 33.

Raman effect on the evolution of polarization in low-birefringence fiber

ZHANG Si-Yuan1, JIA Wei-Guo1, WANG Yu-Ping2, WANG Mei-Jie1, Menke Nei-Mu-Le1

(1. School of Physical Science and Technology, Inner Mongolia University, Hohhot 010021, China;2. Academic Affairs Office, Inner Mongolia Radio & TV University, Hohhot 010010, China)

In low birefringence fiber, by solving the coupled nonlinear Schrodinger equations containing the Raman effect for satisfying right- and left-handed circularly polarized light in the quasi-CW case, the normalized power and the phase difference analytic solutions have been obtained. Using the analytic solutions, the expressions of ellipticity and azimuth angle have been deduced and the influences of Raman effect and the transmission distance on the polarization state evolution have been researched, the relationships of ellipticity and azimuth angle with input power were described by using the phase plane method. The results show that the Raman effect and the transmission distance are the main factors that affect the stability of polarization, the polarization state evolution cycles of ellipticity and azimuth angle can be changed and the oscillation amplitude also can be changed for the low birefringence fiber in the transmission process.

Low-birefringence optical fiber; Raman effect; The polarization state; Ellipticity; Input power

国家自然科学基金(61167004);内蒙古自治区研究生科研创新(14020202)；内蒙古自然基金(2014MS0104)

张思远(1989—),男，陕西省榆林市横山县人，硕士，主要从事非线性光学的研究.E-mail: zsy244479842@126.com

贾维国.E-mail: jwg1960@163.com

103969/j.issn.1000-0364.2015.10.020

O436

A

1000-0364(2015)05-0841-07

投稿日期:2014-05-06