5d过渡金属原子掺杂氮化铝纳米管电子结构、磁性性质的第一性原理计算

王 鹏, 陈依心, 耿朝晖, 张梓璇, 蔡丹云, 郑宇斐, 张召富, 周铁戈

(1. 南开大学电子信息与光学工程学院, 天津 300071; 2. 天津大学精密仪器与光电子工程学院, 天津 300072)

5d过渡金属原子掺杂氮化铝纳米管电子结构、磁性性质的第一性原理计算

王 鹏1, 陈依心1, 耿朝晖1, 张梓璇1, 蔡丹云2, 郑宇斐1, 张召富1, 周铁戈1

(1. 南开大学电子信息与光学工程学院, 天津 300071; 2. 天津大学精密仪器与光电子工程学院, 天津 300072)

采用基于密度泛函理论(DFT)的第一性原理计算方法, 研究了5d过渡金属原子(Lu、Hf、Ta、W、Re、Os、Ir、Pt、Au、Hg)取代AlN纳米管(AlNNTs)中的铝原子或氮原子时体系的几何结构、电子结构和磁性性质; 并且以理想AlN纳米管(AlNNTs)、Al缺陷体系(VAl)和N缺陷体系(VN)的结果作为对比. 研究发现: 5d 原子取代Al(Al5d)时体系的局域对称性接近于C3v, 但是取代N(N5d)时体系的局域对称性偏离C3v对称性较大; 当掺杂的5d元素相同时, Al5d的成键能比N5d的成键能大; 当掺杂体系相同时(Al5d或N5d), 其成键能基本上随着5d原子的原子序数的增大而降低; 掺杂体系中出现了明显的杂质能级, 给出了态密度等结果; 不同掺杂情况的磁矩不同, 总磁矩呈现出较强的规律性. 利用C3v对称性和分子轨道理论解释了过渡金属原子取代Al时杂质能级的产生和体系磁性的变化规律.

第一性原理计算; 氮化铝纳米管; 5d过渡金属原子; 分子轨道理论

1 引 言

石墨烯[1]、碳纳米管(CNTs)[2,3]、氮化硼纳米管(BNNTs)[4,5]、六方氮化硼单层(h-BN)[6,7]、氮化铝纳米带(AlNNR)[8]、氮化铝纳米管(AlNNTs)[9]等低维纳米材料, 因其独特的结构和优良的力学、热学和光学性能, 在自旋电子学[10,11]、纳米电子学等领域有重要的研究和应用价值, 对于新型电子器件的制备具有理论指导意义. 在AlN纳米管中化学键主要是共价键, 但是因为两种组分在电负性上有较大的差别, 所以其中存在相当大的离子键成份, 它决定着各结构相的稳定性等性质. 2002年, Tondaer 等依据气相和固相之间的平衡原理利用相浓缩的办法合成了氮化铝纳米管[9]. 他们在直流放电反应器中利用利用铝和氮气反应得到直径在30-200 nm之间的长度为500-700 nm的氮化铝纳米管和纳米粒子; 2003年, Hu等同样利用通过将金属铝氮化获得氮化铝纳米管[12], 他们将掺杂CoSO4的金属Al放入水平管状炉充入氢气后加热至900℃, 然后将炉内气体换成NH3/N2混合气体, 继续将反应炉加热到1100℃后再持续90分钟得到氮化铝纳米管. 2005年, Yin等利用纳米管作为模板得到共轴的C-AlN-C纳米管状复合物[13]. 通过掺杂或者吸附其它原子, 可以改变AlNNTs的几何结构、电子结构、磁性等物理特性, 从而可以设计出新型自旋电子学结构单元. 然而, 到目前为止我们还没有看到采用5d原子掺杂AlNNTs的相关研究见诸报道, 尤其是电子结构和磁性方面的结果.

本文采用密度泛函理论(Density Functional Theory, 简记为DFT)[14-16], 系统研究了5d过渡金属原子取代AlNNTs中的铝原子(Al5d)、氮原子(N5d)等体系的几何结构、电子结构和磁性性质; 为了作为对比, 给出了理想AlNNTs (pure-AlNNTs)以及Al缺陷(VAl)和N缺陷(VN)体系. 特别地, 利用杂质原子的局域对称性和分子轨道理论知识, 解释了Al5d体系的杂质能级产生和磁矩的变化规律. 本文介绍我们的研究方法、结果及理论分析.

2 理论模型与计算方法

采用(5, 5)纳米管的原胞, 它是由5个N原子和5个Al原子围成的一个原胞. 同时为了避免掺杂金属与相邻的原胞之间的相互影响, 计算中采用10×(5, 5)超胞, 即未掺杂的AlNNTs是由50个N原子与50个Al原子组成, 并且用5d原子取代其中的一个Al原子或者一个N原子进行掺杂计算. 图1为AlIr、NIr、VAl和VN体系的几何结构.

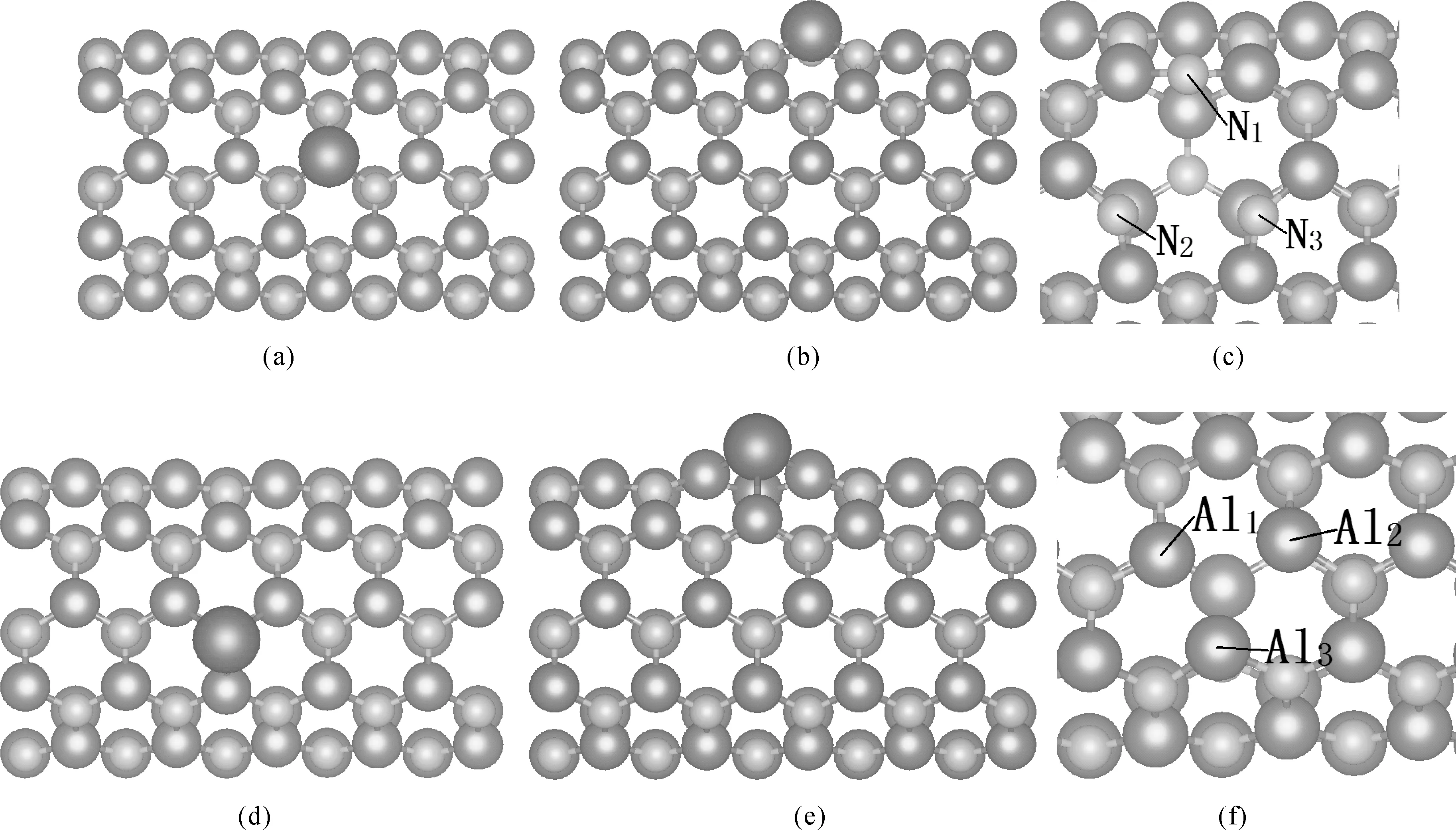
图1 AlIr、VAl、NIr和VN体系的几何结构模型(a)AlIr俯视图；(b)AlIr主视图；(c)VAl俯视图；(d)NIr俯视图；(e)NIr主视图；(f)VN主视图.(蓝色较大原子，Al原子，绿色较小原子是N原子，红色原子是Ir原子)Fig. 1 Geometry models of AlIr, VAl, NIr, and VN (a) Top view of AlIr; (b) Main view of AlIr; (c) Top view of VAl; (d) Top view of NIr; (e) Main view of NIr; (f) Top view of VN. (the blue bigger balls are Al atoms, the green smaller balls are N atoms, the single red ball is Ir atom)

研究中采用第一性原理计算和理论分析相结合的方法. 使用基于密度泛函理论的软件包SIESTA (Spanish Initiative for Electronic Simulations with Thousands of Atoms)[17]进行计算, 用Perdew, Burke和Ernzerhof (PBE)[18]的广义梯度近似(GGA)来描述交换关联能. 基组是数值原子轨道的线性组合(Linear combination of atomic orbitals). 计算中Al、N和5d原子的价电子组态分别如下: Al:3s2p1, N:2s2p3, Lu:5d16s2, Hf:5d26s2, Ta:5d36s2, W:5d46s2, Re:5d56s2, Os:5d66s2, Ir:5d76s2, Pt:5d96s1, Au:5d106s1, Hg:5d106s2. 对于Al和N, 采用双ζ轨道(DZ)展开价电子波函数, 对于5d原子采用双ζ极化轨道(DZP)展开价电子波函数. 实空间网格划分的等效平面波截断能设定为220 Ry. (1 Ry = 13.6 eV).

计算过程由两部分进行: 首先进行几何结构优化, 得到稳定的几何结构, 然后对优化后的体系的电子结构和磁性性质进行静态计算. 几何结构优化中, 采用1×1×3的k点网格(Gamma为中心, M-P方案自动生成), 电子弛豫精度设定为10-4eV, 收敛判据为作用到每个原子上的力小于0.02 eV·Å-1. 静态计算中取1×1×5的k点网格, 电子弛豫精度设定为10-5eV.

3 计算结果与讨论

3.1 几何结构

优化之后的pure-AlNNTs中Al-N键长是1.839 Å, 最近临的两个N原子的距离是3.170 Å, 最近临的两个Al原子的距离是3.149 Å, 与其它报道相吻合[16]. VAl和VN体系相比于pure-AlNNTs发生形变. 具体而言, 在图1(e)中, 缺陷的Al周围的三个N原子都远离缺陷中心, N1-N2, N2-N3, N3-N1的距离分别为4.246 Å, 3.752 Å, 4.296 Å; 在图1(f)中, 缺陷N周围的三个Al原子形状发生畸变, Al1-Al2, Al2-Al3, Al3-Al1之间的距离分别为3.152 Å, 3.365 Å, 2.700 Å. 5d原子掺杂优化后的各个体系的晶格参数以及成键能E的数据如表1所示.

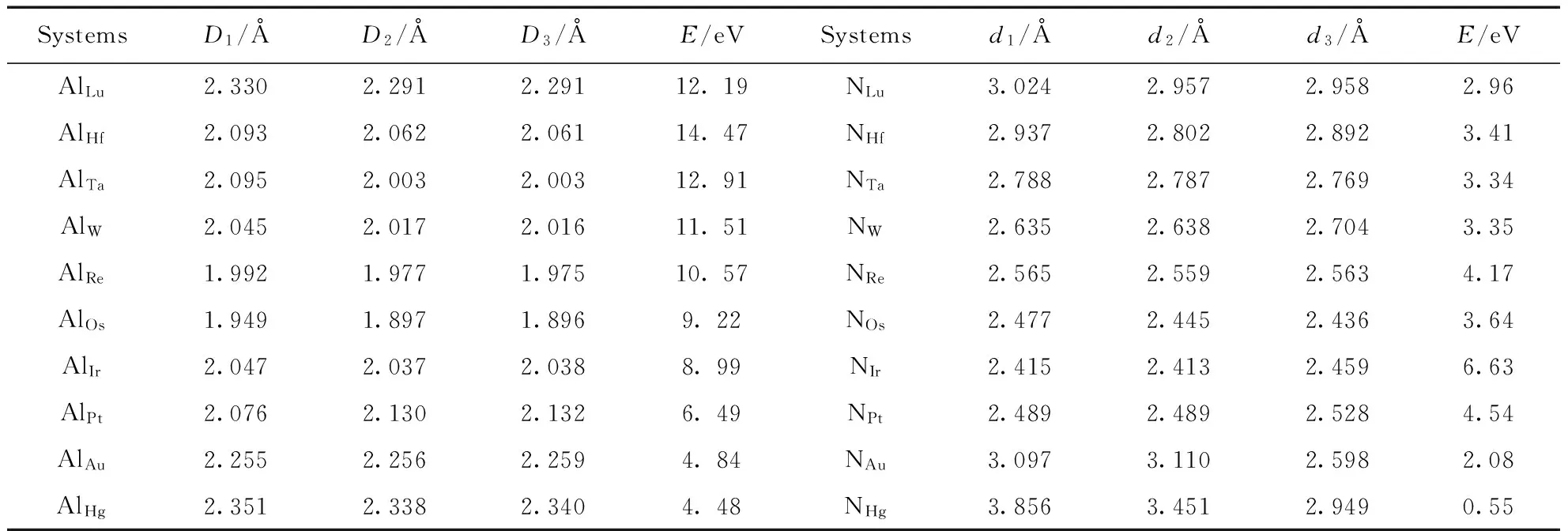
表1 5d原子掺杂AlNNTs结构参数

表中的D1、D2、D3代表Al5d体系中的5d原子与最近的3个N原子的距离,d1、d2、d3代表N5d体系中的5d原子与最近的3个Al原子的距离.这些晶格参数可以反映出掺杂体系的形变情况. 定量地看, N5d中5d原子与最近的Al的距离明显大于Al5d中同一个5d原子与最近的N原子的距离, N5d形变较大. 5d原子取代Al原子之后, 优化之后的几何结构具有非常接近C3v的局域对称性; 取代N时, 偏离C3v对称性较大, 晶格畸变比较明显. 特别的, 当Hf、Hg、Au取代N原子时, 对称性严重偏离C3v. 例如Au取代Al原子时, 与最近的3个N原子的距离分别是2.255 Å, 2.256 Å, 2.259 Å, 接近C3v的局域对称性; 而Au取代N原子时, 与最近的3个Al原子的距离分别是3.097 Å, 3.110 Å, 2.598 Å, 严重偏离C3v的局域对称性. 对于Al5d体系而言, Re掺杂时与最近的3个N原子的距离最小, 对于N5d体系而言, Ir掺杂时与最近的3个Al原子的距离最小.

E是成键能. 对于Al5d, 成键能E的计算方法为:E=EVAl+E5d-Eall, 对于N5d, 成键能的计算方法为:E=EVN+E5d-Eall. 其中,EVAl表示VAl体系的总能量,EVN表示VN体系总能量,E5d表示独立的杂质原子的能量,Eall表示优化后的体系的总能量. 成键能可以反映出掺杂体系的结构稳定性, 成键能大的体系稳定性更高. 从表1中可以明显看出同一个5d原子进行掺杂时, Al5d的成键能比N5d明显要大, 即Al5d体系比N5d更加稳定, 5d原子更有利于取代Al. 另外, 对于Al5d或者N5d, 成键能基本上随着5d原子的原子序数的增大而降低, 表明5d原子序数越小的掺杂体系越稳定. 特别的, NHg成键能仅为0.5535 eV, 明显小于其他体系的成键能, 表明Hg取代N时, 体系更接近于物理吸附, Hg原子与周围的Al原子没有形成化学键. 值得注意的是, 本研究组进行的5d过渡金属原子掺杂氮化硼纳米管计算得出了相似的几何结构规律[19].

3.2 电子结构

计算得到的各个体系的总态密度(TDOS)如图2和图3所示, 图2(a)到(l)中分别给出了Lu、Hf、Ta、W、Re、Os、Ir、Pt、Au、Hg取代AlNNTs中的Al原子及Al缺陷和pure-AlNNTs体系的DOS图. 图3(a)到(k)中分别是Lu、Hf、Ta、W、Re、Os、Ir、Pt、Au、Hg取代AlNNTs中的N原子及N缺陷体系的DOS. 其中虚线表示费米能级.

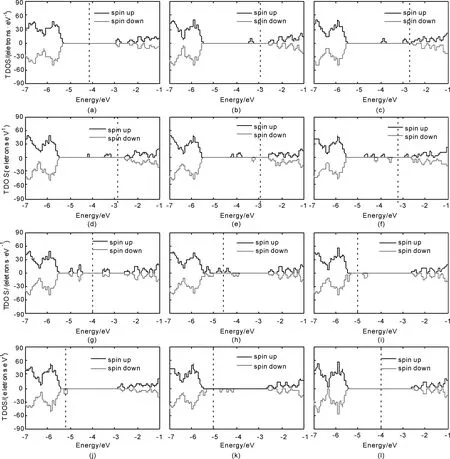
图2 5d原子取代Al原子等体系的DOS (a) AlLu; (b) AlHf; (c) AlTa; (d) AlW;(e) AlRe;(f) AlOs; (g) AlIr; (h) AlPt; (i) AlAu; (j) AlHg; (k) VAl; (l)pure-AlNNTsFig. 2 The total density of states of Al5d systems (a) AlLu; (b) AlHf; (c) AlTa; (d) AlW;(e) AlRe;(f) AlOs; (g) AlIr; (h) AlPt; (i) AlAu; (j) AlHg; (k) VAl; (l)pure-AlNNTs

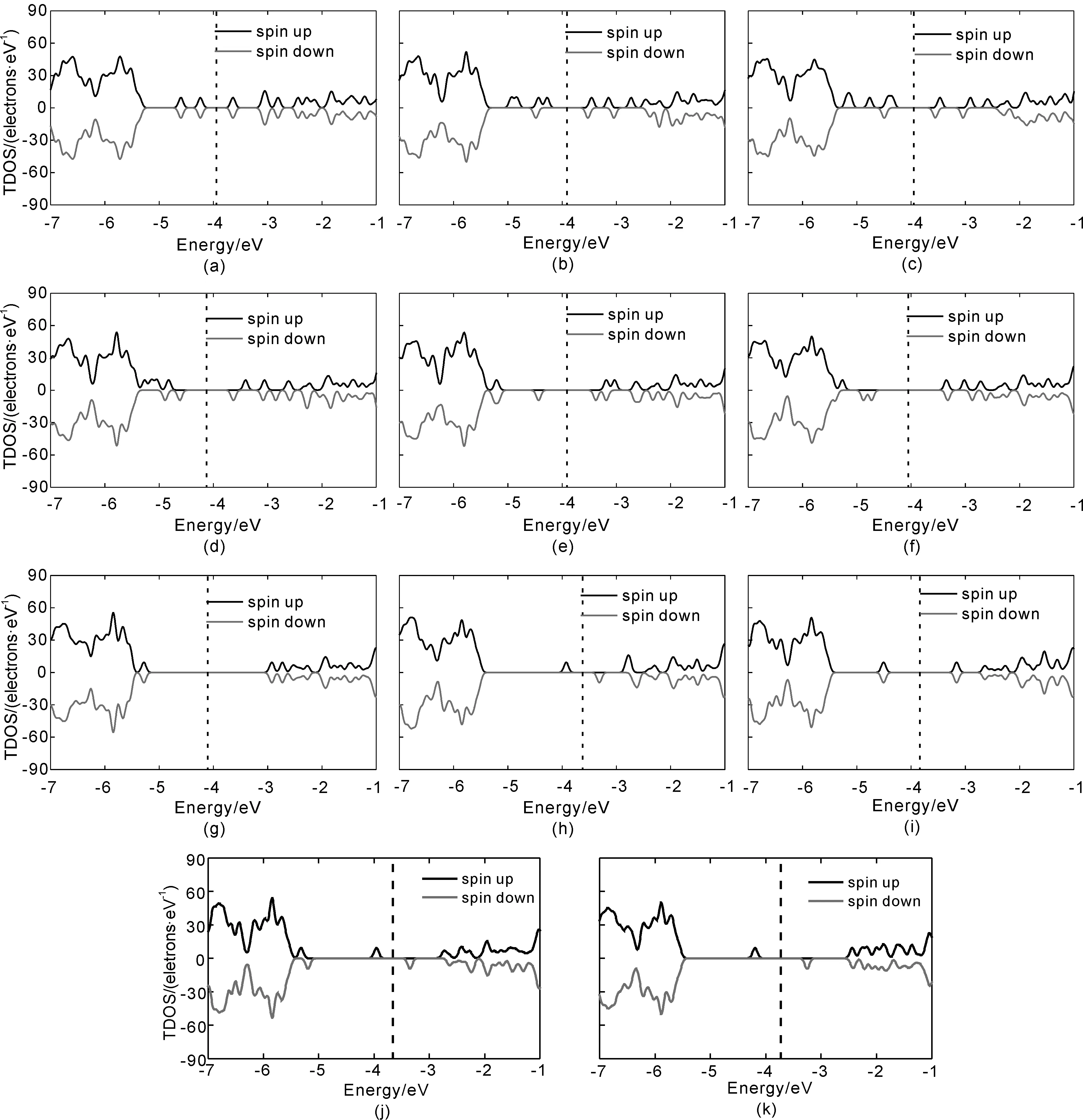
图3 5d原子取代N原子等体系的DOS(a) NLu; (b) NHf; (c) NTa; (d) NW;(e) NRe;(f) NOs; (g) NIr; (h) NPt; (i) NAu; (j) NHg; (k)VNFig. 3 The total density of states of N5d systems (a) NLu; (b) NHf; (c) NTa; (d) NW;(e) NRe;(f) NOs; (g) NIr; (h) NPt; (i) NAu; (j) NHg; (k)VN

从图2和图3中可以看出, 掺杂体系的禁带中出现了明显的杂质能级. 例如: 在图2(a)AlLu中, 在-2.874 eV处存在杂质能级, 并且TDOS呈对称分布;图2(b)AlHf中, -3.339 eV, 处存在自旋向上的能级; 图2(c) AlTa中, 在-3.867 eV处和-2.909 eV处存在自旋向上的杂质能级; 图2(d)AlW中在-4.191 eV, -3.367 eV, -3.246 eV处有自旋向上的杂质能级.

由于N5d体系严重偏离C3v对称性, 使得在图3的N5dDOS中, 杂质能级比同一5d原子取代Al原子时要复杂, 例如在图3(a)NLu中, 在-4.606 eV, -4.244 eV, -3.644 eV, -3.062 eV和-2.806 eV处存在杂质能级, 并且TDOS呈对称分布; 图3(b)NHf中, 在-4.928 eV, -4.833 eV, -4.439 eV, -4.283 eV, -3.461 eV, -3.144 eV和-2.722 eV处存在自旋向上的杂质能级, 在-4.489 eV, -3.511 eV和-3.033 eV处存在自旋向下的杂质能级; 图3(c) NTa中, 在-5.144 eV, -4.766 eV, -4.388 eV, -3.472 eV, -2.905 eV和-2.588 eV处有自旋向上的杂质能级, 在-4.483 eV, -3.556 eV和-5.050 eV处存在自旋向下的杂质能级.

3.3 磁性性质

表2给出了5d原子掺杂AlNNTs超胞的总磁矩(Ms)以及杂质原子(M5d)、与杂质原子最近邻的3个N原子(MN1,MN2,MN3)或者3个Al原子(MAl1,MAl2,MAl3)及VAl、VN的局域磁矩和总磁矩.

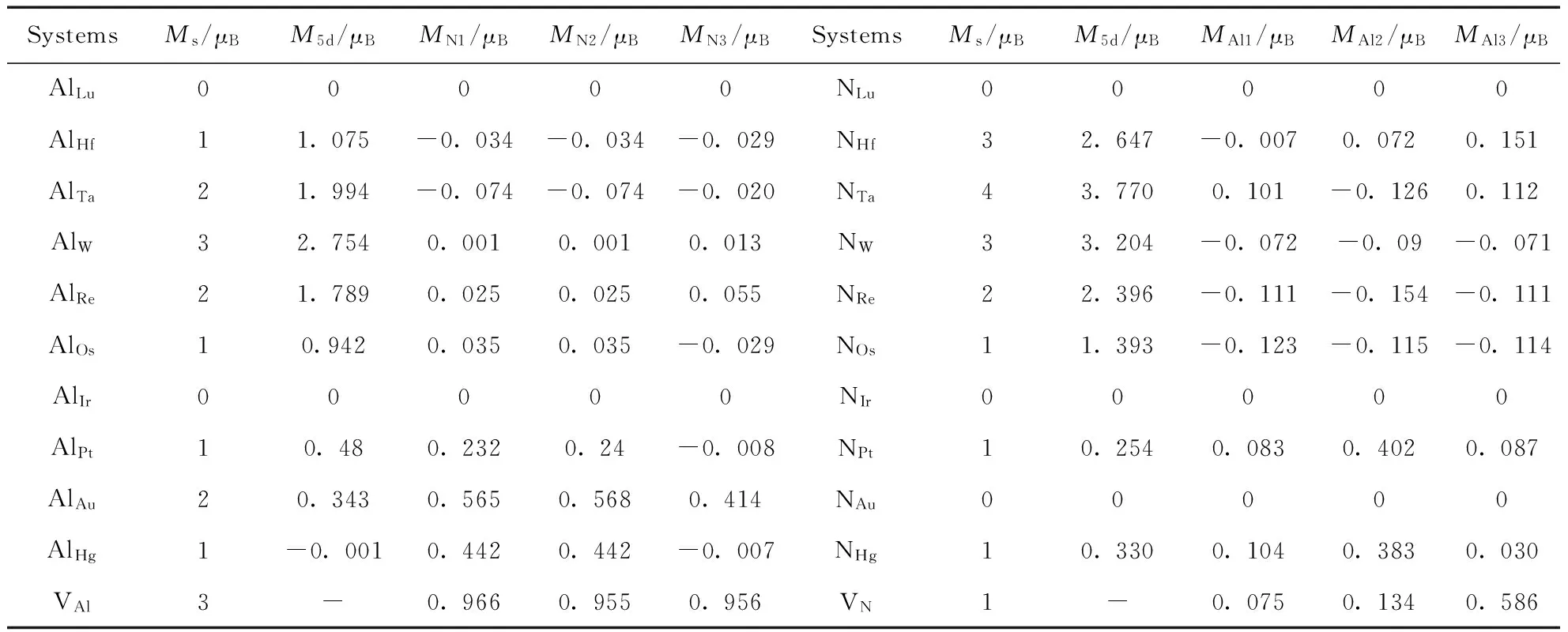
表2 5d原子取代AlNNTs中的Al、N原子体系的磁矩

从表2可以看出, 不同的掺杂体系总磁矩不同, 这是由5d原子的价电子排布随着原子序数增大而变化以及不同掺杂体系的对称性存在差异造成的; 各个掺杂体系的局域磁矩主要分为三类, 第一类是局域磁矩主要分布在5d原子上, 包括Al5d中的AlHf、AlTa、AlW、AlRe、AlOs以及N5d中的NLu、NHf、NTa、NW、NRe、NOs; 第二类是局域磁矩主要分布在5d原子最近邻的Al或者N原子上包括Al5d中的AlHg. 第三类是局域磁矩在5d原子及其最近邻的Al原子或N原子上均有较大分布局, 包括AlAu、AlPt、NPt、NHg. 另外, AlLu、AlIr、NLu、NIr、NAu这五个体系的总磁矩以及局域磁矩都是零.

前面已经分析出, Al5d系统有较好的C3v的局域对称性, 总磁矩也有着较为明显的规律性分布, 而N5d的局域对称性严重偏离C3v, 磁矩分布特征较为混乱. 下面我们采用分子轨道理论, 探究出Al5d系统的杂质能级和磁矩的产生原因. 图4中给出了Al5d体系的分子轨道和杂质能级示意图.

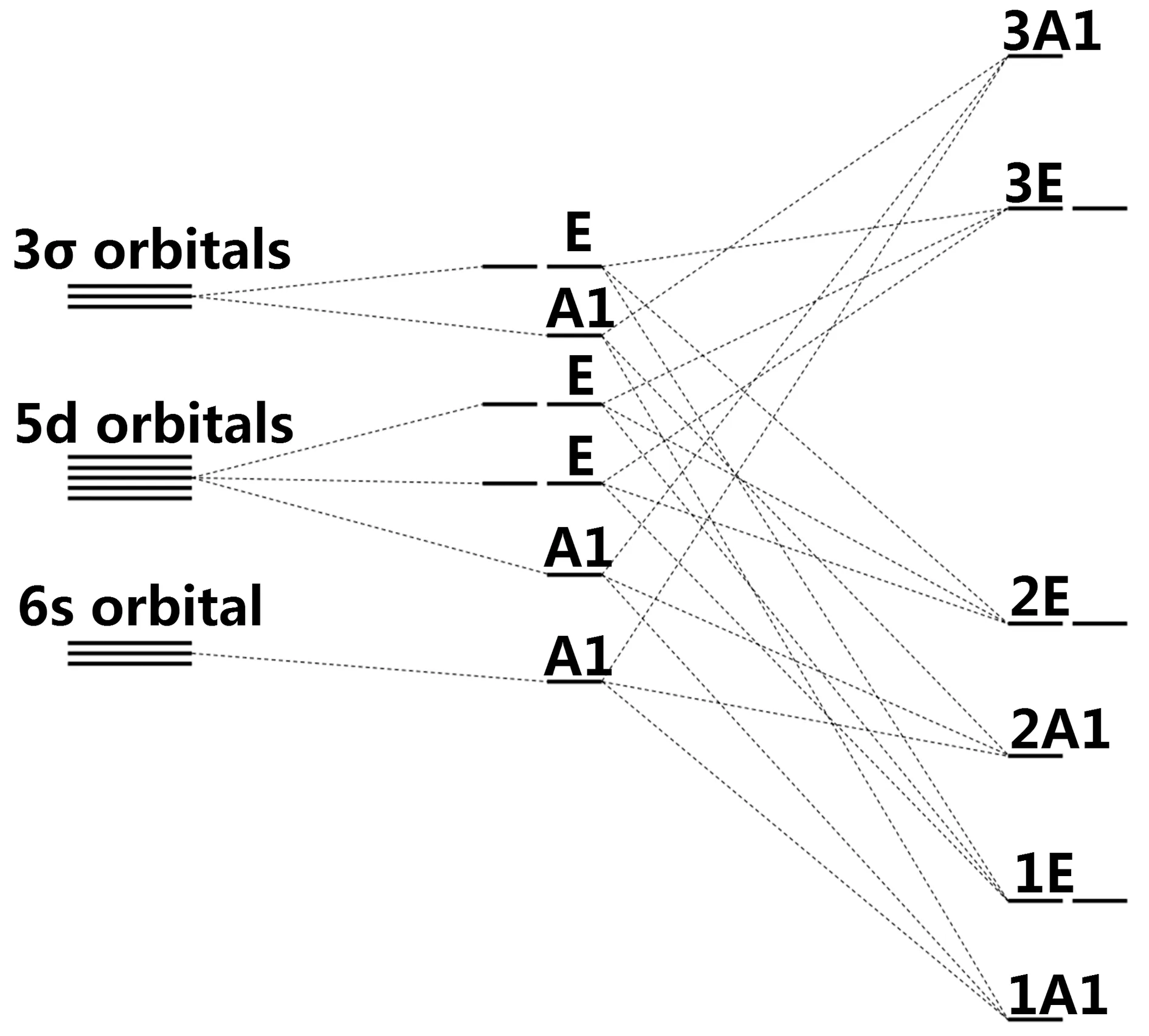
图4 Al5d体系的分子轨道和能级示意图Fig. 4 Schematic molecular orbital and energy level diagram for Al5d

从理想的AlNNTs中去掉一个Al原子后, 与缺陷原子最近邻的3个N原子上存在3个σ悬挂键, 它们在C3v对称性下分裂为A1和E两个轨道.掺杂原子的5d轨道分裂为A1, E, E三个轨道, 而6s轨道本身就具有A1对称性. 轨道杂化时, 具有相同对称性的轨道彼此杂化, 生成3个具有A1对称性的分子轨道和3个具有E对称性的分子轨道, 按能量高低依次排列为1A1、1E、2A1、2E、3E、3A1.

对于Lu原子, 其价电子组态为5d16s2, 具有3个价电子, 加上杂质原子最近邻的3个N原子上的3个未配对电子, 掺杂体系共有6个电子, 它们按照能级高低依次填充分子轨道. 由于1E和2A1之间分裂很大, 6个电子会完全占据1A1和1E能级(自旋向上和向下都占满), 使得AlLu体系总磁矩为0. 对于Hf原子, 价电子组态为5d26s2, 共4个价电子, 加上周围3个N原子上的3个未配对电子, 掺杂体系共7个电子, 其中6个电子把1A1和1E轨道完全占据, 剩余的一个电子占据在2A1轨道, 2A1能级处于半充满状态, AlHf总磁矩应为1 μB. 在图2(b)中可以看出-3.307 eV位置处2A1能级的存在, 自旋向上, 而且被电子占据. Ta原子取代Al原子时掺杂体系共8个电子, 其中6个电子把1A1和1E轨道完全占据. 由于2A1能级和2E能级能量差别不大, 另外2个电子在2A1能级和2E能级自旋同向分布, 因此AlTa体系总磁矩应为2 μB. 在图2(c)中可以看到-3.839 eV处和-2.936 eV处有自旋向上的杂质能级. W取代Al时掺杂体系共9个电子, 其中6个电子把1A1和1E轨道完全占据, 另外3个电子在2A1能级、2E能级自旋同向分布,因此AlW总磁矩应为3 μB. 图2(d)中-4.175 eV、-3.386 eV、-3.236 eV处有自旋向上的杂质能级. Re掺杂时掺杂体系共10个电子, 其中6个电子完全占据1A1和1E能级, 其余4个电子中, 3个自旋向上、1个自旋向下填充于2A1和2E能级, 这是因为2E和3E之间的劈裂很大. 所以AlRe体系的总磁矩应为2 μB, 并且在图2(e)的DOS中可以清晰看出, 费米能级之下的杂质能级是3个自旋向上(其中两个能级的位置重合)1个自旋向下. Os掺杂时掺杂体系共11个电子, 6个电子填充于1A1和1E, 另外5个电子填充在2A1和2E(3个自旋向上2个自旋向下), 因此导致AlOs总磁矩为1μB. 对于Ir, 掺杂体系共12个电子, 它们把1A1、1E、2A1、2E轨道完全占据, 这导致AlIr体系的总磁矩应为0, 图2(g)中DOS对称分布. Pt相对于Ir, 多出一个电子, 这个电子填充在3E能级上, 使得AlPt总磁矩为1 μB. Au比Ir多出2个电子, 这2个电子以自旋向上的方式同时填充在3E能级上, 使得AlAu总磁矩为2 μB. Hg比Au多出一个电子, 这个电子以自旋向下方式填充在3E能级, 因而AlHg总磁矩为1 μB.

4 结 论

基于密度泛函理论, 采用第一性原理计算方法, 系统研究了AlNNTs中的Al原子缺陷、N原子缺陷以及5d过渡金属原子掺杂体系的几何结构、电子结构和磁性性质, 研究发现: 各种掺杂体系的几何结构主要接近于C3v, 但是N5d的对称性明显偏离了C3v, 对于同一个掺杂原子, 取代Al的掺杂体系的成键能比取代N的掺杂体系的成键能高; 对同一种掺杂类型而言, 成键能基本上随着掺杂原子的原子序数的增大而减小; 受电子排布和对称性的影响, 不同掺杂体系的磁矩分布不同, 其中AlLu、AlIr、NLu、NIr和NAu的总磁矩为0, AlHf、AlPt、AlHg、NOs、NPt和NHg的总磁矩为1 μB, AlTa、AlRe、AlAu和NRe的总磁矩是2 μB, AlW、AlOs、NHf和NW的总磁矩为3 μB, NTa的总磁矩为4 μB. 采用分子轨道理论, 结合对称性, 解释了5d原子取代Al原子时的杂质能级以及磁矩变化规律.

[1] Novoselov K S, Geim A K, Morozov S V,etal. Electric field effect in atomically thin carbon films [J].Science, 2004, 306 (5696): 666.

[2] Iijima S. Helical microtubules of graphitic carbon [J].Nature, 1991, 354 (6348): 56.

[3] Li Y, Yang M, Zhao H B. Magnetic field effect on the electronic structure and optical properties of single-walled carbon nanotubes [J].J.At.Mol.Phys., 2013, 30 (5): 838 (in Chinese) [李勇, 杨谋, 赵红波. 磁场对单壁碳纳米管电子结构和光学性质的影响 [J]. 原子与分子物理学报, 2013, 30 (5): 838]

[4] Rubio A, Corkill J L, Cohen M L. Theory of graphitic boron nitride nanotubes [J].Phys.Rev. B, 1994, 49 (7): 5081.

[5] Chopra N G, Luyken R J, Cherrey K,etal. Boron nitride nanotubes [J].Science, 1995, 269 (5226): 966.

[6] Jin C, Lin F, Suenaga K,etal. Fabrication of a freestanding boron nitride single layer and its defect assignments [J].Phys.Rev.Lett., 2009, 102 (19): 195505.

[7] Zhang Z F, Zhou T G, Zuo X. First-principles calculations of h-BN Monolayers by doping with oxygen and sulfur [J].ActaPhys.Sin., 2013, 62 (8): 83102 (in Chinese) [张召富, 周铁戈, 左旭. 氧、硫掺杂六方氮化硼单层的第一性原理计算 [J]. 物理学报, 2013, 62 (8): 83102]

[8] Wu Q, Hu Z, Wang X Z,etal. Synthesis and optical characterization of aluminum nitride nanobelts [J].J.Phys.Chem. B, 2003, 107 (36): 9726.

[9] Tondare V N, Balasubramanian C, Shende S V,etal. Field emission from open ended aluminum nitride nanotubes [J].Appl.Phys.Lett., 2002, 80 (25): 4813.

[10] Fert A. Nobel Lecture: Origin, development, and future of spintronics [J].Rev.Mod.Phys., 2008, 80(4): 1517.

[11] Prinz G A. Magnetoelectronics [J].Science, 1998, 282 (5394): 1660.

[12] Wu Q, Hu Z, Wang X Z,etal. Synthesis and characterization of faceted hexagonal aluminum nitride nanotubes [J].J.Am.Chem.Soc., 2003, 125 (34): 10176.

[13] Yin L W, Bando Y, Zhu Y C,etal. Single-crystalline AlN nanotubes with carbon-layer coatings on the outer and inner surfaces via a multiwalled-carbon-nanotube-template-induced route [J].Adv.Mater., 2005, 17 (2): 213.

[14] Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects [J].J.Phys.Rev., 1965, 140 (4A): A1133.

[15] Hohenberg P, Kohn W. Inhomogeneous electron gas [J].Phys.Rev., 1964, 136 (3B): B864.

[16] Nie Z X, Wang L J. First-principles study of the effects of single N vacancy on the electronic structure and ferromagnetism of Cu-doped AlN [J].J.At.Mol.Phys., 2013, 30 (2): 299 (in Chinese) [聂招秀, 王腊节. N空位对Cu掺杂AlN电磁性质的影响的第一性原理研究 [J]. 原子与分子物理学报, 2013, 30 (2): 299]

[17] Junquera J, Ghosez P. Critical thickness for ferroelectricity in perovskite ultrathin films [J].Nature, 2003, 422 (6931): 506.

[18] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple [J].Phys.Rev.Lett., 1996, 77 (18): 3865.

[19] Zhang Z F, Geng Z H, Wang P,etal. Properties of 5d atoms doped boron nitride nanotubes: a first-principles calculation and molecular orbital analysis [J].ActaPhys.Sin., 2013, 62 (24): 246301 (in Chinese) [张召富, 耿朝晖, 王鹏, 等. 5d 过渡金属原子掺杂氮化硼纳米管的第一性原理计算 [J]. 物理学报, 2013, 62 (24): 246301]

Electronic and magnetic properties of 5d atoms doped aluminium nitride nanotubes: a first-principles calculation

WANG Peng1, CHEN Yi-Xin1, GENG Zhao-Hui1, ZHANG Zi-Xuan1,CAI Dan-Yun2, ZHENG Yu-Fei1, ZHANG Zhao-Fu1, ZHOU Tie-Ge1

(1. College of Electronic Information and Optical Engineering, Nankai University, Tianjing 300071, China; 2. School of Precision Instrument and Optoelectronics Engineering, Tianjin University, Tianjing 300072, China)

A first-principles calculation based on density functional theory is carried out to reveal the geometry, electronic structure and magnetic properties of aluminium nitride nanotubes (AlNNTs), whose Al/N atoms are substituted by 5d atoms (Al5dor N5d). The pure-AlNNTs and AlNNTs with Al vacancy (VAl) and N vacancy (VN) are also investigated for comparison. Results show that the local symmetry of Al5dsystem is similar toC3v, while the N5dsystem exhibits a large geometric deviation fromC3v. When AlNNTs are doped by the same 5d atom, the bonding energy of Al5dis higher than that of N5d; when 5d atoms substitute for Al/N atoms, the bonding energy of system decreases along with the atomic number growth. There exist obvious impurity energy levels in the band gap, and the densities of states (DOSs) are presented. The total magnetic moment differs from each other when doped by different atoms, and the total magnetic moments of doped systems present a strong regularity. The impurity energy levels and total magnetic moments are explained by the molecular orbital theory underC3vlocal symmetry.

First-principles calculation; AlN nanotubes; 5d atoms; Molecular orbital theory

2014-07-08

天津自然科学基金(13JCQNJC00500); 南开大学百项工程(BX11254)

王鹏(1993—), 男, 河北省唐山市滦南县人, 主要研究领域为第一性原理计算.

张召富. E-mail: zzfu@mail.nankai.edu.cn

103969/j.issn.1000-0364.2015.10.011

O472+.4

A

1000-0364(2015)05-0783-08