质子碰撞氦原子单电离全微分截面的后碰撞作用和扭曲效应

段月花, 苏 婷, 孙世艳, 贾祥福

(山西师范大学物理与信息工程学院, 临汾 041004)

质子碰撞氦原子单电离全微分截面的后碰撞作用和扭曲效应

段月花, 苏 婷, 孙世艳, 贾祥福

(山西师范大学物理与信息工程学院, 临汾 041004)

用扭曲波方法，推广了修正的库仑波恩(MCB)近似计算到重离子碰撞He原子电离问题计算.检查了对75 keV 质子碰撞氦原子单电离的全微分截面的应用情况.结果表明，现在的方法定性地产生了实验的峰结构，尤其是在垂直平面.应用MCB方法研究这一碰撞体系中的后碰撞(PCI)效应，发现PCI效应对全微分截面的形状在散射平面和垂直平面都有着强烈的影响.同时，分析了扭曲效应对全微分截面的贡献.表明，随着动量转移的增加，扭曲效应的作用变得越来越重要.尤其是，扭曲效应定性解释了负角区域的结构.

全微分截面； 后碰撞作用； 扭曲效应

1 Introduction

Ionization processes in the field of ion-atom collision have been studied for several decades[1-5]. Because this type research gives a way to understand few-body associated with the quantum dynamics, and the results can be vastly used in many fields[1-4].With the continuous development of the experiment technique known as COLTRIMS (cold-target recoil-ion momentum spectroscopy)[2,6], the usually tiny projectile's scattering angle can be indirectly obtained by measuring the ionized electron and recoil ion momenta. Consequently, fully differential cross sections (FDCS) for ion impact can be measured with high precision, and provide a very stringent test of the theory. In 2006, kinematically complete experiments have been performed by Schulzetal.[7]for single ionization of helium by 75 keV proton impact in the complete three-dimensional space. Interestingly, some unexpected structures are founded. Such studies have proven to be extremely powerful as they yield fully differential cross sections and therefore provide the most sensitive tests of theoretical models describing few-body dynamics in ionization processes. However, on the theoretical side, only a limited number of calculations have been carried out for the fully differential cross sections. For example, the continuum distorted wave-eikonal initial state (CDW-EIS) method[8]and the three-body distorted wave (3DW) method[2]have been extended to calculate the FDCS for single ionization of helium by proton impact in the scattering and perpendicular planes. But the GA method[9]and 6DW method[10]even have not been used to calculate the out-of-plane. Furthermore, although the calculations can qualitatively reproduce some structures, there are still substantial differences between theoretical predictions and experiment, especially for the perpendicular plane. Therefore, further theoretical analysis and calculations seem to be appropriate and necessary.

The generation of unexpected structures, which were found from the measurement data, have been reported due to the high-order effects[7]. For instance, the well-known two-peak structure at aboutθe=±30oand the interesting minimum atθe=0oin the perpendicular plane[11]was explained in terms of the interference between the projectile-ejected electron and the projectile-target core (PI) interactions in P+He. Many theories have been used to explain the role of PCI and PI for ion impact. The results showed that the PCI and PI effects are considerable important. Therefore, we will apply the extended modified Coulomb-Born approximation theory[12]to analyze the FDCS for the single ionization of helium by proton impact at the incident energy of 75 keV in both the scattering plane and the perpendicular plane. At the same time, we employ the present method to examine that the angular distribution of the ejected electron can be significantly influenced by the postcollision interaction.

We also detailedly assess how the distorted effects contribute to the structure of the emission pattern in both the scattering plane and the perpendicular plane. It is showed that the major contribution to the cross-section around the binary peak in the scattering plane and structures in the perpendicular plane comes from the initial channel perturbation potential. But with the increasing transverse momentum transfersqt(the transverse component of momentum transfersq), the contribution of the distorted effects becomes more and more important to the FDCS in both scattering and perpendicular planes. Atomic units are used throughout unless otherwise noted.

2 Theoretical method

Let us consider the following reaction produced by the impact of a bare ion of nuclear chargeZpon a He atom of nuclear chargeZT

Zp+(ZT,2e-)→Zp+(ZT,e-)+e.

(1)

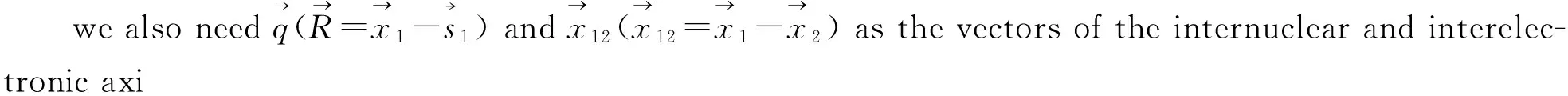
H=Hi+Vi,

(2)

whereHirepresents the Hamiltonian in the entrance channel, andViis the corresponding perturbation potential. In the initial channel, one may write

,

(3)

(4)

(5)

Here

Vi′ =Vi+Vid,

(6)

.

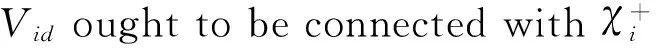
(7)

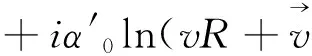
(8)

The Schrödinger equation defining in the entrance channel is given by (Hi-E)φi=0. The unperturbed stateφireads as

(9)

Fortheinitialstateofhelium,wehavechosentheanalyticalfittotheHartree-FockwavefunctiongivenbyByronandJoachain[13]

φ(x1,x2)=U(x1)U(x2),

(10)

whereU(x)=(4π)-1/2(2.60505e-1.41x+2.08144e-2.61x).

With the help of (2), we can rewrite Eq. (7) in the equivalent form

〉.

(11)

Inserting (8) into Eq. (11) and resorting to the usual mass limit μ≫1, one readily identifies the additional distorting potentialVidas

(12)

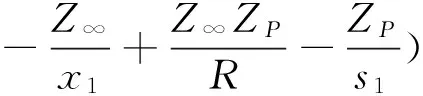
(13)

withtheasymptoticchargeZ∞=1. For the eigenfunction ofHwe assume the form

(14)

whereψ-is the solution of the three-body Schrodinger equation

(15)

An approximate expression for the wavefunction reads[15,16]

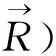
χe(αTe,p,x1)χ(αPe,K,s1).

(16)

χ(α,k,r)=e-πα/2Γ(1-iα)1F1

(17)

ThesymbolsΓand1F1representthegammafunctionandtheconfluenthypergeometricfunction,respectively.TheSommerfeldparametershavetheform

(18)

Thewavefunctionψ-(calledCDW)representsinteractionsbetweentwobodysubsystemssincethedistortioneffectsofeachtwo-bodyCoulombpotentialhavebeentreatedexactly.AnuncertainpointofthismodelrepresentstheuseoftheasymptoticchargeZ∞=1.ItisshowedthattheCDWwavefunction(16)isasymptoticallycorrectinallasymptoticdomainsofcoordinatespace,asdetailedinRefs.[17-19].Thismeansthattheabovewavefunctionistheleadingtermoftheexactscatteringwavefunctionifanytwoparticlesarefarapart.ThiscompletesthederivationnecessaryfortheformulationofthepresentmodelcalledhereafterthemodifiedCoulomb-Born(MCB)approximation[12].TostudythePCIeffectwehavemadecalculationsneglectingthePCI(αPe=0)toshowhowimportantistoadequatelymodelthisinteractioninasingleionizationprocess.TheMCBhasbeenusedforthetotalcrosssectioninasemiclassicalway.ThisisthefirsttimefortheMCBtocalculatetheFDCSinaquantum-mechanicalway.AndthePIinteractionistakenintoaccountintheinitialandfinalstatewavesinaCoulombdistortedwave.

Thefullydifferentialcrosssectionsfortheprocess(1)maybewrittenas

(19)

whereNeisthenumberofelectronsintheatomicshell, dEerepresentstheenergyintervaloftheejectedelectron,andthesolidanglesdΩPanddΩedenotethedirectionofscatteringoftheprojectileandtheejectedelectron,respectively.

Combining(5)and(6)wecansplitthetransitionamplitudeequation(5)asthesumoftwoscatteringamplitude

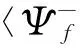
(20)

3 Results and discussion

Inthissection,wewillchecktheaccuracyoftheMCBmodelusingtheequation(19),andbrieflyanalyzehowthehigh-ordereffectsPCIinfluencetheFDCS.Furthermore,wewillevaluatehowthedistortedeffectsinfluencethestructureoftheemissionpatterninboththescatteringplaneandtheperpendicularplane.

InFig. 1,wepresenttheresultsfortheMCBandMCB-noPCIandtheircomparisonstotheexperimentaldataextractedfromRef. [7].Thetheoreticalcalculationsandexperimentaldatacorrespondto75keVprotonsingleionizationofhelium,forelectronsejectedinthescatteringplanewithanenergyof5.4eV,anddifferenttransversemomentumtransfersqtof0.13a.u., 0.41a.u., 0.73a.u., 1.38a.u..Forcomparisonconvenientlywithotherdata,thepresentcalculationsaremultipliedbyaproperfactorwhichisshowninthefigurecaptionstopreservetheinformationontherelativemagnitudeofthedifferenttheoreticalpredictions.

Fig. 1 Fully differential cross-sections for electrons with an energy 5.4 eV ejected into the scattering plane in 75 keV p+He collisions. θe corresponds to the ejected electron angle. The transverse momentum transfers are qt of 0.13 a.u., 0.41 a.u., 0.73 a.u., 1.38 a.u. (from bottom to top). The dotted vertical lines indicate the angles θq and -θq,n.. Dotted lines: MCB-noPCI calculations. Solid lines: MCB calculations. Solid circles: experimental data[7]

Anothervisiblestructurenearθe= -35o,unrelatedtoboththebinaryandrecoilpeaks,atthelargestqtisproperlyreproducedbytheMCBresults.WhenthePCIisignored,thereisaprofoundimpactonthemagnitudeandpositionofthestructurenearθe=-35°.Recently,the3Cmodel[11]reproducestheshapeofthisstructureduetoaninterferenceatthelargestqtwhichcanbejustanextensionoftheexplanationbasedonthePIinteraction.Therefore,high-ordereffectsisveryimportantinreproducingthestructurenearθe=-35°.

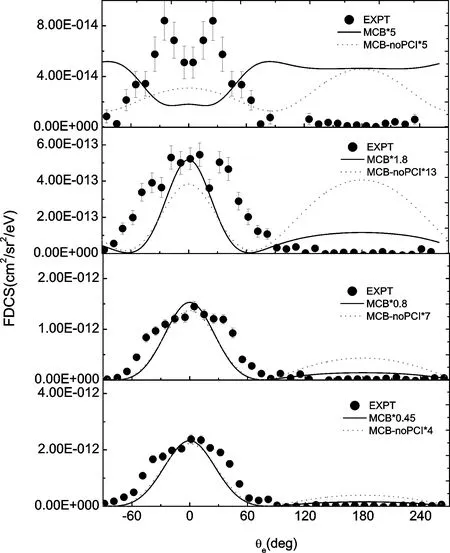
Fig. 2 Same as in Fig. 1 except that this plane is the perpendicular plane

ToexplorethephysicaloriginofthepeakstructureintheFDCS,weexaminethecontributionoftheadditionaldistortionpotentialtotheFDCSinthescatteringandperpendicularplanes.ThecrosssectioniscalculatedasacoherentsumofcontributionsofperturbationpotentialscatteringamplitudeTivanddistortionpotentialscatteringamplitudeTid.InFigs. (3)and(4)theseparate(incoherent)contributionsofTivandTidscatteringamplitudesaredisplayed.

FromFig.3,themajorcontributiontothecross-sectionaroundthebinarypeakcomesfromtheperturbationpotential(seeeq. (4))inthescatteringplane.Interestingly,thepartialcross-sectionsarisingfromthedistortedpotential(seeeq. (12))qualitativelyreproducethestructuresatnegativeanglesatallqtintheexperimentaldata.Itisseenthatthedistortedpotentialmakesasignificanteffectontheresultsforsmallqt(seeFig. 3(a), (b)and(c)),andmakesitbetteratthelargestqtwheretheshapeofthepeaknearθe=-35°isnotreproducedbytheMCBtheorywithoutthedistortedpotential.AdestructiveinterferenceofTidandTivleadstoacross-sectionsmallerthantheindividualincoherentamplitudeTivatsmallqt(seeFig. 3(a)and(b)).ButitisalmostthesamewiththemeasurementwhethertheTidisswitchedonoroffatqt=0.73a.u..WhenatthelargestqttheconstructiveinterferenceofTidandTivmakesthecross-sectionslargerthantheindividualincoherentamplitudeTiv,whilesmallerthantheindividualincoherentamplitudeTivatlargeanglesregionsothatthecross-sectionsbecomeclosertothemeasurement.Obviously,withtheincreasingqttheroleoftheindividualincoherentamplitudeTidbecomesmoreandmoreimportanttotheFDCS.

Fig. 3 Same as in Fig.1 except that the incoherent contributions to the FDCS of the perturbation potential scattering amplitude Tiv (dash lines) and distortion potential scattering amplitude Tid (dotted lines)

ThereareseveralimportantobservationstobemadefromtheresultspresentedinFig. 4.Theperturbationpotentialisstillthemaincontributiontothecross-sectiontoreproduceallstructuresintheperpendicularplane.AdestructiveinterferenceofTidandTivleadstoacross-sectionsmallerthantheindividualincoherentamplitudeTivforallcases.Meanwhile,withtheincreasingqt,similartothescatteringplane,thecontributionoftheindividualincoherentamplitudeTidbecomesmoreandmoreimportanttotheFDCS.Therefore,itisseenthatthereisalittledifferencebetweenthecrosssectionsarisingfromtheindividualincoherentamplitudeTivandfromthetwointerferenceamplitudesatsmallqt(seeFig. 4(a), (b)and(c)),insteadofthesecases,theindividualincoherentamplitudeTidmakestheresultsreducedbyanorderofmagnitudeatthelargestqt.Furthermore,bothexperimentandtheoryhavethesamecharacteristicshapeatlargeanglesrangewherehasnoanypeakatthelargestqt,andwhiletheamplitudeTidisswitchoff,anobviouslowvalleyisobserved.However,theagreementisworsefortheminimumatthelargestqt.ItisinterestingthatattheminimumaslightpeakemergingintheindividualincoherentamplitudeTivbecomesmoreapparentduetotheindividualincoherentamplitudeTidtakingpartin.ThefailureoftheMCBmodelpredictingthefeatureinthisgeometrymaybetracedbacktoanimmaturedescriptionoftheamplitudeTiv.

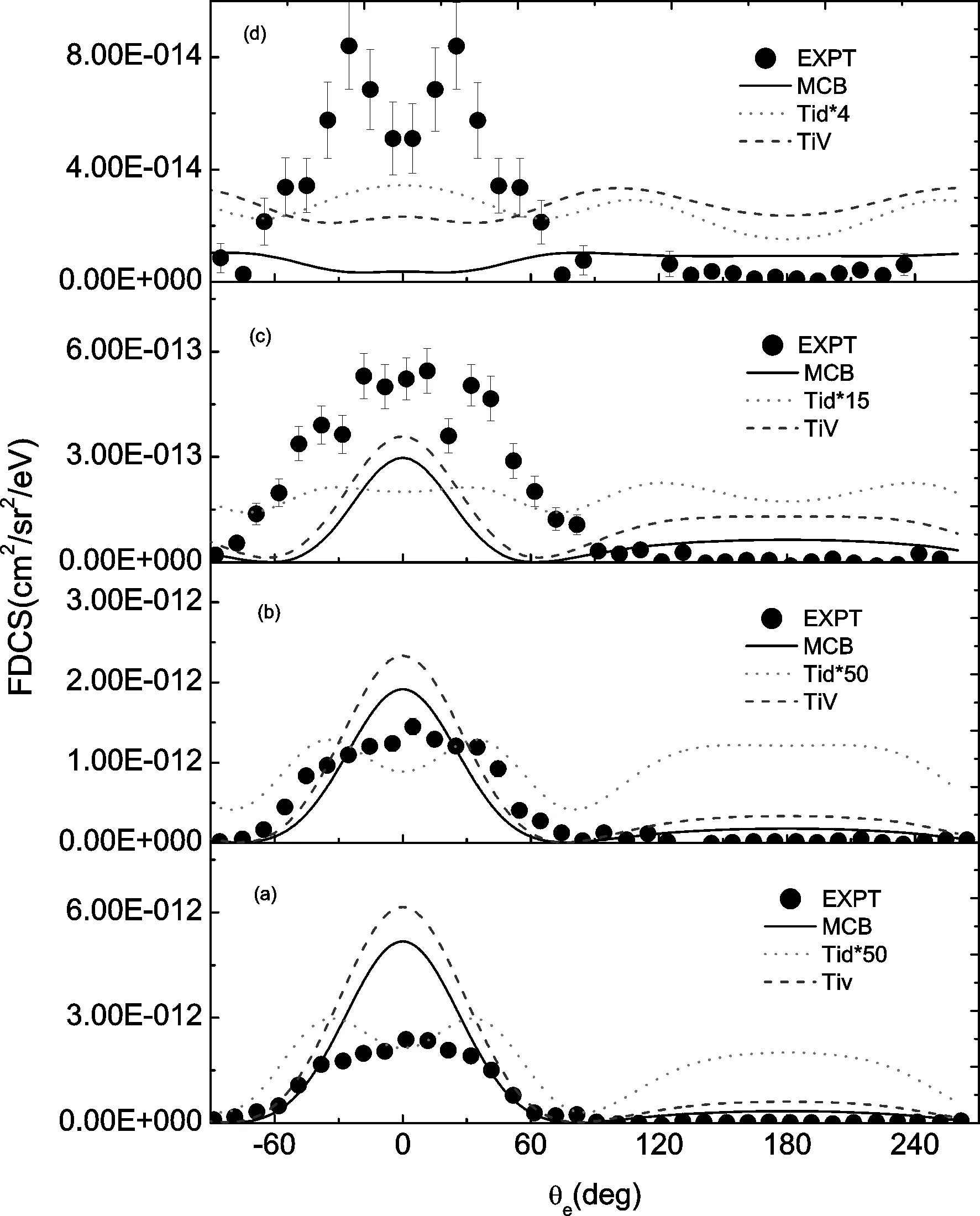
Fig. 4 Same as in Fig. 2 except that the incoherent contributions to the FDCS of the perturbation potential scattering amplitude Tiv (dash lines) and distortion potential scattering amplitude Tid (dotted lines)

4 Conclusions

WepresenttheMCBcalculationsoftheFDCSforsingleionizationofheliumby75keVprotonimpactinboththescatteringplaneandtheperpendicularplane.ItisfoundthatsomesignificantimprovementswiththedataareachievedwiththefullMCBresults,especiallyforthetwo-peakstructureatthelargestqtintheperpendicularplane.Both3DW[7]andCDW-EIS[11]calculationsdonotqualitativelyreproducethetwo-peakstructureintheperpendicularplane,butMCBcalculationsdo.However,someobviousdiscrepanciesstillremain.Theagreementbetweenexperimentandtheoryisbetterinthescatteringplanethanitisintheperpendicularplane.SothedescriptionofthesephenomenaintheMCBapproachisevidentlypremature.Furtherimprovementshouldbeproposedtoaccountforthis.Inaddition,weassessthepostcollisioninteractionbycomparingtheresultsoftheMCBandMCB-noPCI,itisshowedthatthePCIhasaprofoundimpactontheshapeofthefullydifferentialcrosssectioninboththescatteringplaneandtheperpendicularplane.ThusthePCIisimportantenoughsothatitshouldnotbeneglected.

WehavealsodiscussedthecontributionsofthedistortedpotentialandtheperturbationpotentialtotheFDCSinthepresentmodel.Itisfoundthattheinterferenceeffectisveryintenseinboththescatteringplaneandtheperpendicularplane.Wecanseethattheshapeofthebinarypeakinthescatteringplaneandthetwo-peakstructureintheperpendicularplaneatthelargestqtmainlydependontheperturbationpotentialscatteringamplitudeTiv.However,withtheincreasingqtthecontributionoftheindividualincoherentamplitudeTidbecomesmoreandmoreimportanttotheFDCS.Noticeably,inthescatteringplane,thepartialcross-sectionsarisingfromthedistortedpotentialqualitativelyreproducethestructuresatnegativeanglesregionatallqtintheexperimentaldata.Furthermore,thepeaknearθe=-35°isqualitativelyreproducedduetothedistortedeffectsatthelargestqt.Therefore,theshapeandpositionofthepeakareprimarilydeterminedbytheamplitudeTivandthenmodifiedbytheamplitudeTid.However,theinterpretationofthesefeaturesmighthavebeenratherincomplete.Soamoredefinitiveexplanationneedstobefurtherstudied.

[1] Rescigno T N, Baertschy M, Isscas W A,etal. Collisional breakup in a quantum system of rhree charged particles [J].Science, 1999, 286: 2474.

[2] Schulz M, Moshammer R, Fischer D,etal. Three-dimensional imaging of atomic four-body processes [J].Nature(London), 2003, 422: 48.

[3] Ehrhardt H, Jung K, Knoth G,etal. Differential cross sections of direct single electron impact ionization [J].Z.Phys. D, 1986, I: 3.

[4] Schulz M, Madison D H. Studies of the few-body problem in atomic break-up processes [J].Int.J.Mod.Phys. A, 2006, 21: 3649.

[5] Ullrich J, Moshammer R, Dorn A,etal. Recoil-ion and electron momentum spectroscopy: reaction-microscopes [J].Rep.Prog.Phys. A, 2003, 66: 1463.

[6] Moshammer R, Ullrich J, Unverzagt M,etal. Low-energy electrons and their dynamical correlation with recoil ions for single ionization of helium by fast, heavy-ion impact [J].Phys.Rev.Lett., 1994, 73: 3371.

[7] Schulz M, Hasan A, Maydanyuk N V,etal. Kinematically complete experiment on single ionization in 75-keV P+He collisions [J].Phys.Rev. A, 2006, 73: 062704.

[8] Ciappina M F, Cravero W R, Schulz M. Post-collisional effects on single ionization in 75-keV P+He collisions [J].J.Phys. B, 2007, 40: 2577.

[9] Dey Ritu, Roy A C. Triply differential cross sections for single ionization of He by proton impact [J].Phys.Lett. A, 2006, 353: 341.

[10] Foster M, Peacher J L, Schulz M,etal. Precollision and postcollision electron-electron correlation effects for intermediate-energy proton-impact ionization of helium [J].Phys.Rev. A, 2005, 72: 062708.

[11] Ma X Y, Li X, Sun S Y,etal. Structures in fully differential cross-sections for proton impact ionization of helium [J].Europhys.Lett., 2012, 98: 53001.

[12] Belkic D. Single electron detachment from H-by proton impact [J].Nucl.Instrum.MethodsJ.Phys. B, 1997, 124: 365.

[13] Byron F W, Joachain C J. Correlation effects in atoms.I.helium [J].Phys.Rev., 1966, 146: 1.

[14] Berakdar J, Briggs J S, Klar H. Proton and antiproton impact ionization of atomic hydrogen and helium [J].Z.Phys. D, 1992, 24: 351.

[15] Garibotti C R, Miraglia J E. Ionization and electron capture to the continuum in the H+-hydrogen-atom collision [J].Phys.Rev. A, 1980, 21: 572.

[16] Brauner M, Briggs J S, Klar H. Triple-differential cross sections for ionisation of hydrogen atoms by electrons and positrons [J].J.Phys. B, 1989, 22: 2265.

[17] Kim Y E, Zubarev A L. Asymptotic continuum wave function for three charged particles [J].Phys.Rev. A, 1997, 56: 521.

[18] Alt E O, Mukhamedzhanov A M. Asymptotic solution of the Schrödinger equation for three charged particles [J].Phys.Rev. A, 1993, 47: 2004.

[19] Mukhamedzhanov A M, Lieber M. Asymptotic wave function for three charged particles in the continuum [J].Phys.Rev. A, 1996, 54: 3078.

[20] Madison D H, Foster M, Moshammer R,etal. Probing scattering wave functions close to the nucleus [J].Phys.Rev.Lett., 2003, 91: 253201.

[21] Fischer D, Moshammer R, Schulz M,etal. Fully differential cross sections for the single ionization of helium by ion impact [J].J.Phys. B, 2003, 36: 3555.

[22] Schulz M, Najjari B, Voitkiv A B,etal. Postcollision effects in target ionization by ion impact at large momentum transfer [J].Phys.Rev. A, 2013, 88: 022704.

[23] Sharma S, Srivastava M K. Triple-differential cross sections for the electron- and positron-impact ionization of helium in an improved second Born approximation[J].Phys.Rev. A, 1988, 38: 1083.

[24] Jones S, Madison D H. Scaling behavior of the fully differential cross section for ionization of hydrogen atoms by the impact of fast elementary charged particles[J].Phys.Rev. A, 2002, 65: 052727.

[25] Fischer D, Voitkiv A B, Moshammer R,etal. Three-body momentum exchange in singly ionizing 2-MeV/u C6+-helium collisions [J].Phys.Rev. A, 2003, 68: 032709.

[26] Foster M, Madison D H, Peacher J L,etal. Fully differential cross sections for C6+single ionization of helium [J].J.Phys. B, 2004, 37: 1565.

[27] Voitkiv A B, Najjari B, Moshammer R,etal. Three-body quantum dynamics of helium single ionization by 1 GeV/u U92+impact [J].J.Phys. B, 2004, 37: L365.

Postcollision interaction and distorted effects on fully differential cross sections for single ionization of helium by proton impact

DUAN Yue-Hua, SU Ting, SUN Shi-Yan, JIA Xiang-Fu

(School of Physics and Information Engineering, Shanxi Normal University, Linfen 041004, China)

The modified Coulomb-Born (MCB) approximation is applied to study single ionization of helium by 75 keV proton impact. Fully differential cross-sections (FDCS) are calculated using the MCB theory in both the scattering plane and the perpendicular plane for the first time. The results are compared with the experimental data and the MCB without postcollision interaction (MCB-noPCI) calculations. It is found that the present MCB calculations qualitatively reproduce the experimental peak structures, especially in the perpendicular plane. And the PCI has a profound impact on the shape of the fully differential cross section in both the scattering plane and the perpendicular plane. The contribution of the distorted effects to the FDCS is also analyzed in the scattering and perpendicular planes. It turns out that, with the increasing momentum transfers (difference between the initial and scattered projectile momentum), the role of the distorted effects becomes more and more important. In particular, the distorted effects qualitatively predict the structures at negative angles region at all momentum transfers in the scattering plane.

Fully differential cross-sections; Postcollision interaction; The distorted effects

国家自然科学基金(11274215); 山西省自然科学基金(2010011009)

段月花(1989—),女，山西运城人，研究生，研究领域为原子与分子碰撞.

贾祥福.E-mail: jiaxf@dns.sxnu.edu.cn

103969/j.issn.1000-0364.2015.10.013

0561.5

A

1000-0364(2015)05-0796-09

投稿日期: 2014-07-05