TiO薄膜的宽光谱特性椭偏法研究

唐帆斌，肖　峻*，马　孜

(1. 西南民族大学 电气信息工程学院，成都 610041；2. 西南技术物理研究所，成都 610041)

TiO薄膜的宽光谱特性椭偏法研究

唐帆斌1，肖峻1*，马孜2

(1. 西南民族大学 电气信息工程学院，成都 610041；2. 西南技术物理研究所，成都 610041)

摘要：为了获得TiO2薄膜的光学常数，采用德国SENTECH生产的SE850宽光谱反射式光谱型椭偏仪，测量和分析了用光控自动真空镀膜机沉积在K9玻璃上的单层TiO2薄膜，得到了TiO2薄膜在300nm~2500nm宽谱上的光学常数曲线和薄膜厚度。根据TiO2的薄膜特性及成膜特点，考虑了表面粗糙层和界面层对薄膜性能的影响，建模时采用Cauchy指数模型和Tauc-Lorentz模型，对建立的各种模型测量得到的数据进行了分析和比较。结果表明，模型“基底/Tauc-Lorentz模型/表面粗糙层”可以得到最小的均方差为0.5544，得到的TiO2薄膜的厚度的测量值与TFCalc软件的计算值最接近。该研究结果对TiO2薄膜多层膜膜系设计和制备有参考价值。

关键词：薄膜；TiO2薄膜；椭偏仪；薄膜厚度；光学常数

*通讯联系人。E-mail：xiaojun@swun.cn

引言

TiO2在可见和近红外波段具有较高的折射率和良好的化学稳定性和机械性能，在光学薄膜的设计中得到广泛的应用[1]。精确获取薄膜厚度和光学常数(折射率n，消光系数k)是多层膜设计的关键基础数据，随着设计消偏振膜[2]、带通滤波片[3]、多层膜反射镜薄膜[4]和光通信用光学薄膜的膜系层数的增加，微小的光学常数变化会使薄膜的性能发生明显的变化，因而，对薄膜厚度的测量精度要求很高。通常测量薄膜光学常数有光度法、椭偏法和利用波导原理的棱镜耦合法等。椭偏法具有对样品的非破坏性、对环境的非苛刻性和测量的高灵敏度及高精度等优点，还可以获得薄膜的分层结构，逐渐成为测量超薄薄膜和多层膜的厚度和光学常数的一种重要手段。WANG[5]等人利用反射式椭偏仪采用Cauchy色散模型，得到了单层溶胶-凝胶TiO2薄膜在380nm~800nm光谱范围内的厚度和光学常数。WANG[6]等人采用反射式椭偏仪用Cauchy模型较好地描述了溶胶-凝胶制备的SiO2和ZrO2薄膜在300nm~800nm的光学性能。WANG[7]等人考虑膜层的缺陷和非均匀性问题，建立精细的数学模型得到了TiO2薄膜更高精度的厚度和光学常数。国产自制的反射式椭偏仪测量的光谱范围窄，无法覆盖近红外范围，作者使用德国SENTECH生产的SE850反射式光谱型椭偏仪得了单层TiO2薄膜300nm~2500nm的椭偏曲线，用不同的模型对测得的厚度和光学常数进行了分析和比较。

1测量原理

根据椭偏光谱反射光度法理论，偏振光以一定角度入射到薄膜样品时与样品发生相互作用，光的偏振态就会发生变化，椭偏参量(ψ，Δ)通常用下式描述[8]：

(1)

式中，rp和rs分别为在p分量和s分量的菲涅耳反射系数,ψ为偏振角,Δ为p光和s光的反射相位之差。

由测量原理知，从椭偏仪直接得到的是椭偏参量ψ和Δ，但所需要的是光学薄膜的厚度和光学常数(折射率n和消光系数k)等物理量，(1)式是一个超越方程，无法得到解析表达式，一般通过曲线拟合的方法反演得到薄膜的厚度和光学常数。

Cauchy指数模型适用于非金属透明材料光学常数的拟合[9]，折射率n(λ)和消光系数k(λ)的计算公式为：

(2)

(3)

式中,A′，B′，C′，D′，E′和F′都为常数，表征了薄膜的折射率和消光系数的色散特性，也是光学常数反演计算的基本拟合变量;λ是波长。

JELLISON和MODINE于1996年提出了适用于低吸收介质材料和非晶材料色散关系的Tauc-Lorentz模型[10](简写为TL)，是基于Tauc联合态密度和Lorentz振子模型的关系得到的。模型中薄膜的介电函数实部ε1和虚部ε2的表达式为：

(4)

(5)

式中，P为表示积分的柯西主值,τ为时间，ε1(∞)为常数，E为光子能量，E0为跃迁能量，Eg为带隙能量，A为振幅参量，C为展宽参量。TL模型需要拟合的参量有:ε1(∞),E0,Eg,A和C。

对于拟合结果的评价包括两个方面:一是拟合的结果是否符合材料本身的特性；二是看均方差(mean square error,MSE)的大小。MSE的表达式为：

(6)

式中，N是测量次数；M是模型中可变参量的个数；σ是实验数据的测量误差。下标f和m分别表示拟合值和测量值。由(7)式可知，EMSE越小就表示拟合模型与实际数据匹配越好。

2实验与分析

2.1　薄膜制备

实验中采用日本光驰OTFC-1300光控自动真空镀膜机，在K9玻璃基底上沉积单层TiO2薄膜，单层薄膜模型简单易于分析。镀膜机的参量如下：监控波长为700nm，采用光学极值法监控，监控光量信号走值为19.99nm～83.31nm～20.05nm，沉积速率为0.4nm/s，起始压强1.9×10-2Pa，终止压强1.7×10-2Pa，温度保持在200℃。其中离子源参量如下：离子加速电压为1000V，离子流为900mA。

样品的椭偏测量采用德国SENTECH生产的SE850宽谱反射式光谱型椭偏仪，入射角为70°，光谱测量范围为300nm~2500nm，得到TiO2的椭偏宽谱曲线。

2.2　薄膜特性分析

使用TFCalc膜系设计软件，得到700nm的中心波长的单层TiO2薄膜的厚度为120.77nm，作为椭偏仪数据拟合的厚度初始值。

TiO2为低吸收材料，首先采用适用于低吸收材料的Cauchy指数模型，记模型Ⅰ为在 K9玻璃基底上覆盖单层TiO2薄膜，物理模型如表1所示。

Table 1　Three kinds of physical models for TiO2 film

薄膜厚度初值设为120nm，对模型中其它参量进行拟合，拟合后得到的EMSE=8.7174，Ψ和Δ的拟合值与测量值存在较大差异，Ψ和Δ拟合结果如图1所示。

基底表面粗糙度会在薄膜生长过程中使表面产生一层很薄的粗糙层，粗糙层的散射会影响薄膜的性能。在模型Ⅰ的TiO2薄膜上引入描述表面粗糙层(为50%(按厚度，下同)空气和50%TiO2空隙的复合体)的有效介质近似中的Bruggeman模型[11]，表面粗糙层的厚度拟合初值设为3nm，记为模型Ⅱ，物理模型如表1中的第2列所示，可以得到的EMSE显著减小为6.3380，引入表面粗糙层是合理的，但是EMSE的值还不够小，Cauchy模型不能很好地描述TiO2薄膜的宽谱光学特性。

记模型Ⅲ为在K9玻璃基底上覆盖单层TiO2薄膜，选用1阶简谐振子的TL模型，薄膜厚度初值设为120nm，对模型中参量ε1(∞)，E0，Eg，A，C进行拟合，得到的EMSE进一步减小，色散模型与薄膜特性匹配很好。在单层TiO2薄膜上引入表面粗糙层(记为模型Ⅳ)，物理模型如表1中的第2列所示，厚度拟合初值设为3nm，拟合得到的EMSE减小到1.0295，拟合结果非常可信。Ψ和Δ拟合结果如图2所示。

Fig.1　Measured and fitted results of Ψ and Δ of model Ⅰ

Fig.2　Measured and fitted results of Ψ and Δ of model Ⅳ

在模型Ⅳ的基础上，考虑到K9玻璃基底界面的粗糙度会使TiO2薄膜在沉积过程中产生薄膜-基底界面层(等效为50%的K9玻璃和50%的TiO2薄膜)，在基底和TiO2薄膜间引入界面层，物理模型如表1中的第3列所示，记为模型Ⅴ,拟合后的EMSE=1.0151，和模型Ⅳ的EMSE相比差异不是很大，表明薄膜与基底界面之间的杂质和空隙很小，为了减小参量拟合时的关联，认为不存在界面层[12]。

为了得到精度更高的光学常数和更小的EMSE值，当TL模型增加到4阶的Lorentz简谐振子时(记为模型Ⅵ)，拟合的EMSE减小到0.5544。从图3可以看到,Ψ和Δ的拟合曲线与实际测得曲线已经很接近了。同时得到薄膜的折射率随波长的变化曲线，如图4所示。

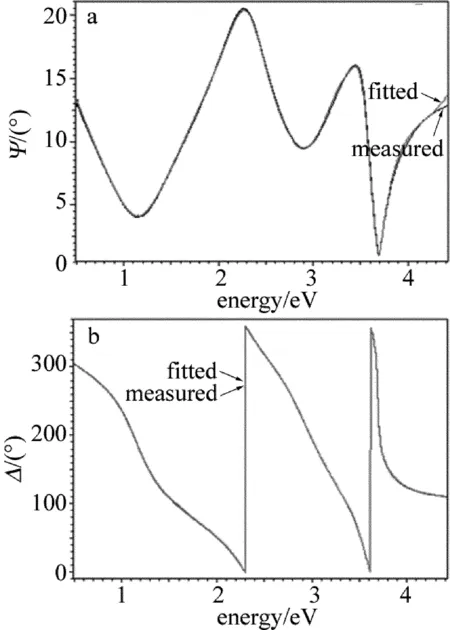
Fig.3　Measured and fitted results of Ψ and Δ of model Ⅵ

Fig.4　Calculated refractive index

表2是上述6种模型拟合得到的各参量表。由表2可看出，模型Ⅳ比模型Ⅱ的EMSE值明显要小得多，从

Table 2　Fitted results of different models

图4中右边的折射率内嵌小图可以看出,折射率在短波区出现了反常色散，采用Cauchy指数模型拟合的结果不好，表明TL模型比Cauchy指数模型更好地描述TiO2薄膜宽光谱椭偏曲线。模型Ⅳ与模型Ⅲ相比，引入了表面粗糙层的EMSE显著减小，折射率增大，说明粗糙层对薄膜光学性质有显著的影响，建立物理模型时不能忽略粗糙层的存在。模型Ⅵ相对于模型Ⅳ，加入了Lorentz简谐振子后,EMSE减小，Ψ和Δ的拟合曲线和实际测量曲线的差异进一步缩小。从模型Ⅲ~模型Ⅵ，EMSE值单调减小，得到的TiO2薄膜厚度和折射率精度越高。由图4可知,在400nm处TiO2薄膜的折射率随波长的变化趋于平稳，与参考文献[6]中所测的TiO2在可见光部分的光学常数测量值变化趋势一致。

3结论

作者采用不同的数学散模型对OTFC-1300光控自动真空镀膜机沉积在K9玻璃基底上的TiO2单层薄膜300nm~2500nm光谱范围的椭偏参量进行了拟合和分析。模型“基底/TL色散模型/表面粗糙层”可准确描述TiO2薄膜的宽谱光学特性。精确测量了TiO2薄膜的厚度，获得了薄膜折射率的宽光谱特性曲线，是进一步在膜系设计中用TiO2作为高折射率材料的基础。

参考文献

[1]PAN Y Q, HANG L X, WU Z S,etal. Influence of ion beam post-treatment on surface roughness of TiO2thin films[J]. Chinese Journal of Lasers, 2010, 37(4):1108-1113(in Chinese).

[2]SHI J H. Analysis and designs of thin films used in infrared non-polarizing beam splitters[D]. Harbin: Harbin Engineering University, 2005: 21-23(in Chinese).

[3]SHEN L, XIONG Sh M, LIU H X,etal. Preparation narrow-band pass filter by dual-ion beams sputtering deposition[J]. Optical Instruments, 2004, 26(2): 87-90(in Chinese).

[4]LEI J H, DUAN H, XING P F,etal. Design of soft X-ray multilayer for familiar spacing layer marerial[J]. Laser Technology, 2011, 35(3): 415-417(in Chinese).

[5]WANG X D, SHEN J, WANG Sh Zh,etal. Optical constants of sol-gel derived TiO2films characterized by spectroscopic ellipsometry[J]. Acta Physica Sinica, 2009, 58(11): 8027-8032(in Chinese).

[6]WANG B Y, YUAN X D, JIANG X D,etal. The optical properties of SiO2and ZrO2films investigated by spectroscopic ellipsometry[J]. Piezoelectrics & Acoustooptics, 2008, 30(6):747-750(in Chinese).

[7]WANG Q, SHEN H, WANG W. Ellipsometry by simulated annealing algorithm[J]. Acta Photonica Sinica, 2008, 37(2):63-65(in Chinese).

[8]AZZAM R M A, BASHARA N M. Ellipsometry and polarized light[M]. Beijing: Science Press, 1986: 103-113(in Chinese).

[9]SYNOWICHI R A. Spectroscopic ellipsometry characterization of indium tin oxide film microstructure and optical constants[J]. Thin Solid films, 1998, 313(1/2): 394-397.

[10]JELLISON G E, Jr, MODINE F A. Parameterization of the optical functions of amorphous materials in the interband region[J]. Applied Physics Letters, 1996, 69(3): 371-373.

[11]BRUGGEMAN D A G. The calculation of various physical constants of heterogeneous substanees.Ⅰ. The dielectric constants and conductivities of mixtures composed of isotropic substances[J]. Annals of Physics, 1935, 24(5):639-791.

[12]HU R. Optical thin film refractive index and thickness testing technology and research[D]. Nanjing: Nanjing University of Science and Technology, 2004:16-17(in Chinese).

Study on wide spectrum characteristics of TiO2film with ellipsometry

TANGFanbin1,XIAOJun1,MAZi2

(1. College of Electrical & Information Engineering, Southwest University for Nationalities, Chengdu 610041, China; 2. Southwest Institute of Technical Physics, Chengdu 610041, China)

Abstract：In order to obtain optical constants of TiO2thin film, single-layer TiO2film deposited on K9 glass with an optical automatic vacuum coating machine was measured and analyzed with a SE850 broadband ellipsometer produced by SENTECH, Germany, and the optical constant curve and thickness of TiO2thin film in 300nm~2500nm spectrum were obtained. Based on the film characteristics and film forming characteristics of TiO2film, taking the influence of the intermix layer and rough surface layer into account, models were set up with Cauchy index model and Tauc-Lorentz model and the measurement data were analyzed and compared. The smallest mean square error of 0.5544 was obtained with a so called model of “substrate/Tauc-Lorentz model/rough surface layer”. The measured TiO2thickness was closest to calculation value of TFCalc software. The results have certain reference value for the design and preparation of TiO2thin multilayer film.

Key words:films; TiO2film; ellipsometer; film thickness; optical constant

收稿日期：2014-09-03；收到修改稿日期：2015-01-07

作者简介：唐帆斌(1989-)，男，硕士研究生，主要从事光学薄膜材料的研究。

中图分类号：O484.5

文献标志码：A

doi:10.7510/jgjs.issn.1001-3806.2015.06.009

文章编号：1001-3806(2015)06-0776-04