基于加权组合核RX算法异物检测及其参量选择
吴香伟,郭宝峰*,陈春种,沈宏海
(1.杭州电子科技大学 自动化学院,杭州 310018;2.中国科学院 长春光学精密机械与物理研究所,长春 130033)
基于加权组合核RX算法异物检测及其参量选择
吴香伟1,郭宝峰1*,陈春种1,沈宏海2
(1.杭州电子科技大学 自动化学院,杭州 310018;2.中国科学院 长春光学精密机械与物理研究所,长春 130033)
摘要:为了融合光谱形状差异信息和多项式核函数全局信息,充分挖掘地物特征,提高异常检测正确率,提出了一种加权组合核RX算法。该算法在高斯核函数的基础上,增加一个光谱角核函数。由于核函数参量和加权参量直接影响算法性能,分别采用了随机函数法、爬山法和粒子群算法对上述参量进行了选择。结果表明,在恒虚警率下使用粒子群算法进行参量设定得到的效果最好,且采用加权组合核函数RX算法得到的目标检测率为83.5%,相对于普通的核RX算法,正确率得到了提高。
关键词:遥感;加权组合核;核RX算法;异物检测;光谱角核;粒子群优化算法
*通讯联系人。E-mail:gbf@hdu.edu.cn
引言
高光谱遥感影像具有较高的光谱分辨率,能够为目标自动检测和识别提供良好的条件[1]。在目标检测中,有许多算法已经取得了较好的结果,但是它们的局限性在于需要被检测目标先验信息。然而,就目前实际应用中,因为缺乏完整的光谱数据库且反射率反演算法不够精确[2-3],所以这些先验信息很难获取。因此,REED和YU提出了基于广义似然比检验的RX方法[4],该方法是一种无先验信息的异常检测算法。
通常来说,在低维空间中高光谱数据是线性不可分的。为解决这个难题,可以通过非线性映射函数,把高光谱数据从低维空间映射到高维特征空间,从线性不可分变成线性可分。由于非线性映射函数未知,所以无法映射到高维特征空间,而利用核函数就不需要知道非线性映射函数的具体形式,只需要选择一个适当的核函数在原始空间中计算即可,间接实现在高维特征空间里进行内积计算。因此,KWON等人提出了基于核的RX算法[5]。在核函数选择方面,先前研究人员使用高斯径向核(Gaussian radial basis kernel,GRBK)函数,但是高斯核是局部特征核,其本身存在一定的局限性。本文中提出一个加权组合核(weighted combination kernel,WCK)函数,该核函数把高斯核和光谱角核线性加权结合,它同时具有高斯核函数的局部性[6]和多项式核函数的全局性,更能充分有效地提取地物信息,提高检测正确率。其中,光谱角核函数(spectral angle kernel,SAK)是由光谱角函数与多项式核函数相结合演变而成,它具有光谱角的检测性能,也具有多项式核函数的全局性能。由于核函数的参量和加权参量的选择影响算法性能的优劣,本文中分别通过随机函数(random,RND)、爬山法(hill climbing method,HCM)和粒子群算法(particle swarm optimization,PSO)3种方式来对参量进行寻优选择。通过3种方法的比较,确定了一个更为有效的方法来设定组合核中的各个参量。
1核RX算法
给定一个原始数据空间X(x∈X),其中数据集合为X=[x(1),x(2),…,x(N)],F是原始空间X通过非线性映射函数φ得到相关联的高维特征空间,φ(X)=[φ(x(1)),φ(x(2)),…,φ(x(N))]为高维特征空间的数据。φ(x)是x映射到F中的对应向量。映射方式为:φ:X→F,x→φ(x)。
利用核函数不需要知道非线性映射函数φ的具体形式,只需要选择使用一个适当的核函数k(·,·)在原空间中计算k(xi,xj)即可,即用原始空间中定义的核函数k(·,·)间接实现高维特征空间中的内积计算。即:
(1)
KWON等人[5]提出的基于核的RX算法对应的特征空间的核算法表达式为:
(2)
式中,Cφ和uφ分别为特征空间中从背景样本估计出的协方差矩阵和均值向量,其表达式分别为:
(3)
(4)
式中,N为高光谱数据像素点个数。因为无需知道非线性映射函数的具体形式,从而避免了在高维特征空间中直接计算内积的复杂过程。
2加权组合核函数
光谱角余弦不仅反映了光谱向量在数值上的差异,也可以反映光谱曲线之间的形状差异,用其作为光谱相似度量具有明显优点。一方面,光谱角是两个光谱向量的夹角,光谱角越大,两个光谱相似度就越小[7];另一方面,由于地物光谱复杂,不同地物光谱存在谱形相似而反射率却相差很大[8]。在此情况下,用光谱角区分不同地物效果更佳。高光谱数据是由高光谱成像仪拍摄采集,采集过程中可能会受到大气污染、天气变化等因素影响,导致采集到的数据不理想,然而物质本身的光谱曲线不容易受外在因素影响。不同物质光谱曲线任具有较大差异,光谱角核函数有利于异常检测。
光谱角核函数具有光谱角的检测性能,也具有多项式核函数的全局性能。它与高斯核函数经过加权有机的结合得到一个加权组合核函数。加权组合核函数具有了高斯核函数的局部性[9-10]和多项式核函数的全局性。加权组合核函数在结构层上面融合了光谱特征和空间特征,相对于单一的核函数来说,更能有效地挖掘辨别地物信息,提高分类精度[11]。
光谱角余弦的数学模型[12]为:
(5)
式中,θ为向量x和向量y的夹角。而多项式核函数[13]为:
(6)
式中,d为多项式函数阶数,c为一个常数。当d=1,c=0时,称为线性核k(x,y)=〈x·y〉;当d≠0,c=0时,称为齐次多项式核k(x,y)=〈x·y〉d。其它称为非线性齐次多项式核。
通过对光谱角余弦函数和多项式核函数相结合的演变得到:
(7)
(7)式为一个非线性齐次多项式。令d≠0,c=0,得到光谱角核函数:
(8)
通过核函数的封闭性质[13],可以得到下面两个线性组合核:
(9)
(10)
因此,加权组合核可以表示为如下形式:
(11)
式中,α是加权系数,fKW是加权组合核函数,fKS是光谱角核函数,fKG=k(x,y)=exp[-‖x-y‖2/(2δ2)]是高斯核函数,δ表示高斯核参量。
利用高斯径向基核函数与光谱角核函数之间的优势互补,将它们组合在一起,构成一个加权组合核函数。加权组合核函数既考虑到了高光谱数据分布特点,也考虑到光谱形状信息,计算光谱曲线的差异,检测出来的高光谱数据信息更加完整,对目标与背景的分辨更加清晰,提高了目标的检测率。其中参量α将控制每个内核的在加权组合核函数中的成分,用来平衡局部特性(高斯内核)和全局特性(光谱角内核)。当α=0时,加权组合核函数将成为单一的光谱角核函数;当α=1时,加权组合核函数变成单一的高斯核函数。
3加权参量及核函数参量优化
在确定核RX算法中的核函数以后,要考虑核函数中的参量和加权参量的选择。加权参量α决定每个核函数在加权组合核函数中的份量,适合的加权参量α能够使每个核函数充分地挖掘出有效的光谱信息。高斯核函数是局部核,主要对相距较近的像素点函数值有影响,而其参量δ就影响函数值,当参量δ比像素点差值(‖x-y‖)小很多,造成过度拟合现象,降低检测能力。相反,参量δ比像素点差值大很多,函数值趋于0,造成不同像素点判为同一类。光谱角核函数具有多项式核函数的全局特性,它对相距较远的像素点函数值有影响,其中参量d对核函数全局推广能力有重要的影响,当d趋于0时,核函数值将为1,形成简单的核矩阵;当d趋于无穷时,核函数值过大,失去组合核函数的优势,并且加大计算量,耗费时间。综合上述原因,加权组合核函数参量对异常检测及其重要,所以本文中将通过对随机函数选择、爬山法和粒子群算法比较,确定一个更为有效的方法用于加权组合核中参量的选择。
3.1 爬山法参量选择
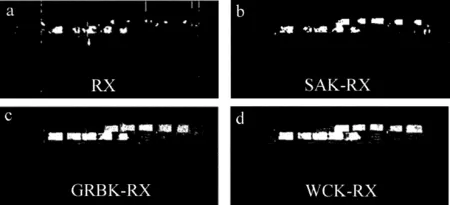
爬山法搜索是一种经典的局部搜索法[14]。它像登山者登高山一样,一直向最高方向持续移动,将达到一个“顶峰”时终止,并且在相邻状态中没有比它更高的值。爬山法不会预测与当前状态不直接相邻的那些状态的值。图1为爬山法搜索流程图,从图中可以看出,爬山法采用多次迭代计算,首先随机选取一个可能解作为目前最优解pbest(此解也成为爬山法的起始解),然后在其邻域内选取另外一个解pnext,如果满足fitness(pnext)>fitness(pbest),则用pnext取代pbest作为当前最优解;如果满足fitness(pnext) Fig.1 Searching flow chart of climbing method 图2为粒子群算法搜索流程图。粒子群算法[15]是EBERHART和KENNEDY于1995年提出,该算法中每个粒子是空间中的一个解,它根据自己的飞行经验和同伴的飞行经验来调整自己的飞行。每个粒子在飞行过程所经历过的最好位置,就是粒子本身找到的最优解。整个群体所经历过的最好位置,就是整个群体目前找到的最优解。前者叫作个体极值(pbest),后者叫作全局极值(gbest)。实际操作中通过由优化问题所决定的适应度值,来评价粒子的“好坏”程度。每个粒子都通过上述两个极值不断更新自己,从而产生新一代群体。 Fig.2 Flow chart of particle swarm optimization algorithm 在每次迭代过程中,通过下式更新速度变量和位置[16-17]: (12) (13) 式中,每个变量的下标i表示第i个粒子,j表示某粒子变量的第j维的量,t表示迭代次数,ω是惯性权重,c1和c2为加速常数,rand1()和rand2()为[0,1]之间的随机数。 ω对粒子的飞行速度有影响,为了提高算法的性能,使用一种自适应调整惯性权重算法。初始确定惯性权重的最大值ωmax和最小值ωmin,随着搜索的进行,惯性权重值线性递减,见以下公式: (14) 式中,tmax为最大迭代次数。 4异常检测过程 异常检测实验的流程如图3所示。首先,实验中分别采用随机函数选择、爬山法、粒子群算法,对加权组合核函数中加权参量及其核函数参量进行选择。由于随机函数选择参量具有随机性,一次的选择并不能代表效果最好的,所以通过多次的参量选择,取其中最好效果与其它方法得到的效果做对比;其次,用最优参量选择方法用于核函数的参量优化选择;最后用RX算法、光谱角核函数RX算法、高斯核函数RX算法与加权组合核函数RX算法对异物检测得到的结果进行对比,来验证加权组合核RX算法的优越性。 Fig.3 Flow chart of anomaly detection 5实验结果与分析 图4是30波段的实测数据的灰度图。实验数据是由中国科学院长春光学精密机械与物理研究所提供的实测高光谱数据,由配准好的80波段的可见近红外光谱数据和75波段的短波红外数据经过波段融合和归一化处理后得到155波段的融合数据。数据大小为226×500的像素点,实验场景包括了以大量植被(矮灌木和杂草)为大背景下的厢式货车1辆、半挂车2辆和无关非目标靶标4个。场景中把10个涂有绿色漆料两类物质作为靶标,其中有5个涂敷军绿铁板和5个涂敷军绿木板作为靶标。 Fig.4 Data of the 30th band 图5是参量选择结果图,其中图5a是30次随机选择参量得到其中一次核RX算法效果最好的结果图,因为随机函数选择的参量具有随机性,所以经过多次选择验证比较,选择最好的一组实验参量作为本方法的代表;图5b、图5c分别是爬山法和粒子群算法选择参量得到的核RX算法结果图;通过实验结果对比确定哪种参量选择方法得到的参量更能有效应用到核函数中。实验数据经过空域滤波处理,有利于去除噪声和改善图像的视觉效果。实验中设置恒虚警率为2.0%的情况下检测目标的正确率,本文中虚警率是背景被错误检测成目标的概率,虚警率越大,背景被错误分成目标越多;虚警率越小,目标检测正确率越小,甚至无法检测出目标。表1是参量实验结果统计表。 Fig.5 Anomaly detection results for three parameter-setting methods αδdaccuracyfalsealarmrateRNDaverage0.53373.634.3122.3%2.0%optimal0.8356.320.9631.6%2.0%HCM0.61734.121.1240.2%2.0%PSO0.721214.362.1183.5%2.0% 实验中随机参量选择具有随机性,一次的结果并不能科学地代表实验最终结果,所以本文中选取30次随机实验结果的平均值和最优值作为该方法的代表。实验的图像结果和参量选择统计表都可说明,随机选择函数方法正确率比较低,最好的一次实验结果正确率是31.6%,平均正确率为22.3%;粒子群优化算法在参量寻优方面是最好的。爬山法寻优参量得到正确率为40.2%,而粒子群寻优参量得到的正确率为83.5%,比爬山法提高了1倍的正确率。粒子群算法比爬山法寻优效果好的原因是,爬山法是个局部寻优算法,它会陷入局部最优,在整体当中可能会有更好的参量,而它无法找到,但是引入惯性权重的粒子群算法具有全局搜索能力,能够有效地防止粒子陷入局部最优,惯性权重随着迭代次数的改变而改变,扩展了单个粒子的空间搜索能力,平衡全局与局部的搜索能力,达到良好搜索效果。实验结果直接表明,核函数中的参量对算法性能至关重要。本文中对参量选择设置了参量的范围,α的范围在0~1之间,δ的范围在0~2000之间,d的范围0~10之间。 异常检测图像结果如图6所示。上面的实验表明,粒子群算法优化核函数中的参量使得加权组合核RX算法异常检测结果最好。所以本实验中的参量都是通过粒子群算法寻优得到。实验中设置恒虚警率为2.0%的情况下,检测并统计目标正确率。表2是异常检测结果统计表。 Fig.6 Results of anomaly detectionwith different methods αδdaccuracyfalsealarmrateRX00037.2%2.0%SAK-RX002.3256.6%2.0%GRBK-RX01038.29080.4%2.0%WCK-RX0.721214.362.1183.5%2.0% 对整体数据的检测结果进行分析,首先在恒虚警率(2.0%)的前提下,使用光谱角核函数、高斯核函数、加权组合核函数的RX算子异常检测目标正确率分别比普通RX算子异常检测目标正确率高出19.4%,43.2%,46.3%。其次,光谱角核RX算子异常检测得到的图像结果和数据统计表的统计结果,有效地说明了光谱角核RX算子异常检测的有效性。光谱角核RX算子异常检测正确率比高斯核RX算子异常检测正确率低 23.8%。这主要原因可能是高光谱数据光谱曲线信息差异较小,光谱的空间分布更符合高斯分布。 两个单一核函数经过加权线性组合构成加权组合核函数以后,取每个单一核函数的优点,去互补其缺点。表2中的数据统计显示,加权组合核RX算法异常检测正确率比高斯核RX算子异常检测正确率高出3.1%,比光谱角核RX算子异常检测正确率高出26.9%。有效说明了加权组合核RX算法异常检测能力更强。 上面提到作者在恒虚警率为2.0%的情况下进行了异常检测(实验)。为什么只选择2.0%的虚警率而不选择其它虚警率,下面专门对此问题进行解析。实验中选择加权组合核RX异常检测算法在虚警率分别为0.5%,1.0%,2.0%,5.0%,10%等情况下验证异常检测目标的正确率,通过对结果的分析来说明为什么选择2.0%的恒虚警率。图7为不同虚警率下异常检测结果图,表3是对应的结果统计表。 Fig.7 Detection results at different false alarm rates falsealarmrate0.5%1.0%2.0%5.0%10.0%accuracy74.6%78.3%83.5%84.6%84.9% 通过对几种不同虚警率下异常检测实验对比可知,随着虚警率的上升,目标的检测正确率也会增大。但是发现虚警率增大到一定程度时,正确率提高的速度缓慢。虚警率从5.0%提高到10%,目标检测正确率却只提高了0.3%,较高的虚警率已经开始影响对目标的判别。虽然低的虚警率也能检测出大部分目标,比如0.5%的虚警率检测正确率为74.6%,但是相对于2.0%的虚警率能检测出83.5%目标、正确率提高了8.9%而言,选择0.5%的虚警率不够好,因为对于异常检测,当然是在不影响辨别目标的前提下正确率越高越好。综合上述原因,本文中选择了2.0%的虚警率来检测异常目标。 6结论 本文中所提出的加权组合核函数解决了原先高斯核RX异常检测只具有局部特性而不具有全局特性的问题,通过增加具有全局特性的光谱角核函数,有效地提高了目标的正确率。在不同的高光谱数据中,根据数据分布的特点和光谱曲线的特点,组合核函数会随着加权参量的变化,可以变成单一的核函数,这样灵活的变化,一个加权组合核函数实际就相当于3个核函数之间的转化。 用实测高光谱数据对本文中提出的加权组合核RX算法异常检测仿真。实验结果表明,本算法相对于一般的核RX异常检测算法,具有较高的目标检测识别率;同时核函数参量影响算法的性能,对异常检测实验结果影响巨大。合理的参量能够使得异常检测正确率提高很多,不合理的参量可能导致无法检测出异常目标,或者检出正确率还不如普通RX异常检测效果。在核函数应用方面只用了具有局部特性的高斯核和全局特性的多项式核函数,后续工作可以尝试选择其它核函数,并且可以同时使用多个核函数进行加权组合。 参考文献 [1]MATTEOLI S, DIANI M, CORSINI G. A tutorial overview of anomaly detection in hyperspectral images [J]. IEEE Transactions on Aerospace and Electronic Systems Magazine, 2010, 25(7): 5-28. [2]ECHES O, DOBIGEON N, TOURNERET J Y. Enhancing hyperspectral image unmixing with spatial correlations [J]. IEEE Transactions on Geosciences and Remote Sensing, 2011, 49(11): 4239-4247. [3]KWON H, DER S Z, NASRABADI N M. Adaptive anomaly detection using subspace separation for hyperspectral imagery [J]. Optical Engineering, 2003, 42(11): 3342-3351. [4]REED I S, YU X L. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(10): 1760-1770. [5]KWON H, NASRABADI N M. Kernel RX algorithm a nonlinear anomaly detector for hyperspectral imagery[J]. IEEE Transactions on Geosciences and Remote Sensing, 2005, 43(2): 388-397. [6]WANG L P, ZHANG L P, HAN J T. Detecting algorithm of moving target in dynamic background based on gray-weighted kernel function [J]. Infrared and Laser Engineering, 2013, 42(12): 3453-3457 (in Chinese). [7]CHEN D R, SUN B, TAO P,etal. Spatial neighboring clustering method for hyperspectral imagery based on kernel spectral angel cosine [J]. Acta Electronica Sinica, 2008, 36(10): 1992-1995(in Chinese). [8]HAN J, YUE J, ZHANG Y,etal. SAM weighted KEST algorithm for anomaly detection in hyperspectral imagery [J]. Journal of Infrared and Millimeter Waves, 2013, 32(4): 359-365(in Chinese). [9]WANG S B. Study on anomaly target detection technology in hyperspectral images [D]. Haerbin: Harbin Institute of Technology, 2010: 22-35(in Chinese). [10]WU X M. The research on hyperspectral imagery unmixing technology based on kernel methods [D]. Hangzhou:Zhejiang University, 2011: 15-33(in Chinese). [11]WANG Ch. Research on multiple kernel learning based target interpretation technologies in hyperspectral imagery [D].Haerbin: Harbin Institute of Technology, 2011: 13-23(in Chinese). [12]GAN P P, WANG R Sh. Spectral remote sensing recognition basis and technology research [J]. Remote Sensing Technology and Application, 2002, 17(3): 53-60(in Chinese). [13]SHAWE-TAYLOR J, CRISTIANINI N. Pattern recognition of kernel method [M]. 2nd ed. Beijing: China Machine Press, 2006: 29-50(in Chinese). [14]DANG J W, WANG Y P, DI F W,etal. Artificial intelligence [M]. Beijing: Electronic Industry Press, 2012: 178-180(in Chinese). [15]EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]//Proceedings of the 6th International Symposium on Micro Machine and Human Science. New York, USA : IEEE , 1995: 39-43. [16]GAO X J. On classification of hyperspectral remotely sensed imagery based on support vector machines[D]. Hangzhou: Hangzhou Dianzi University, 2012: 42-44 (in Chinese) . [17]LIANG Zh J, WANG K F, GU G Q,etal. Digital speckle image correlation method base on particle swarm optimization algorithm[J]. Laser Technology, 2014, 38(5): 603-607 (in Chinese). Anomaly detection based weighted combination kernel RX algorithm and its parameter selection WUXiangwei1,GUOBaofeng1,CHENChunzhong1,SHENHonghai2 (1.School of Automation, Hangzhou Dianzi University, Hangzhou 310018, China;2.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China) Abstract:In order to combine the spectral shape difference information and the polynomial kernel function global information, exploit the object feature fully and improve the accuracy of anomaly detection, anomaly detection method was proposed based on weighted combination kernel RX algorithm. A spectral angle kernel function was added to Gaussian kernel function in the anomaly detection method. Because the kernels’ parameter and the weighting parameter will affect the efficiency of the algorithm, the random function selection, the hill climbing method and the particle swarm optimization algorithm were implemented for setting the above parameters. Experiment results show that at a constant false alarm rate, it is the best to set the parameters by means of the particle swarm algorithm. Target detection rate is 83.5% by using the weighted combination kernel RX algorithm, higher than that by means of the traditional kernel RX algorithm. Key words:remote sensing; weighted combination kernel; kernel RX algorithm; anomaly detection; spectral angle kernel; particle swarm optimization algorithm 收稿日期:2014-10-10;收到修改稿日期:2014-12-01 作者简介:吴香伟(1989- ),男,硕士研究生,主要研究方向为图像处理与目标识别。 基金项目:国家自然科学基金资助项目(61375011);浙江省自然科学基金资助项目(LY13F030015) 中图分类号:TP79 文献标志码:A doi:10.7510/jgjs.issn.1001-3806.2015.06.003 文章编号:1001-3806(2015)06-0745-06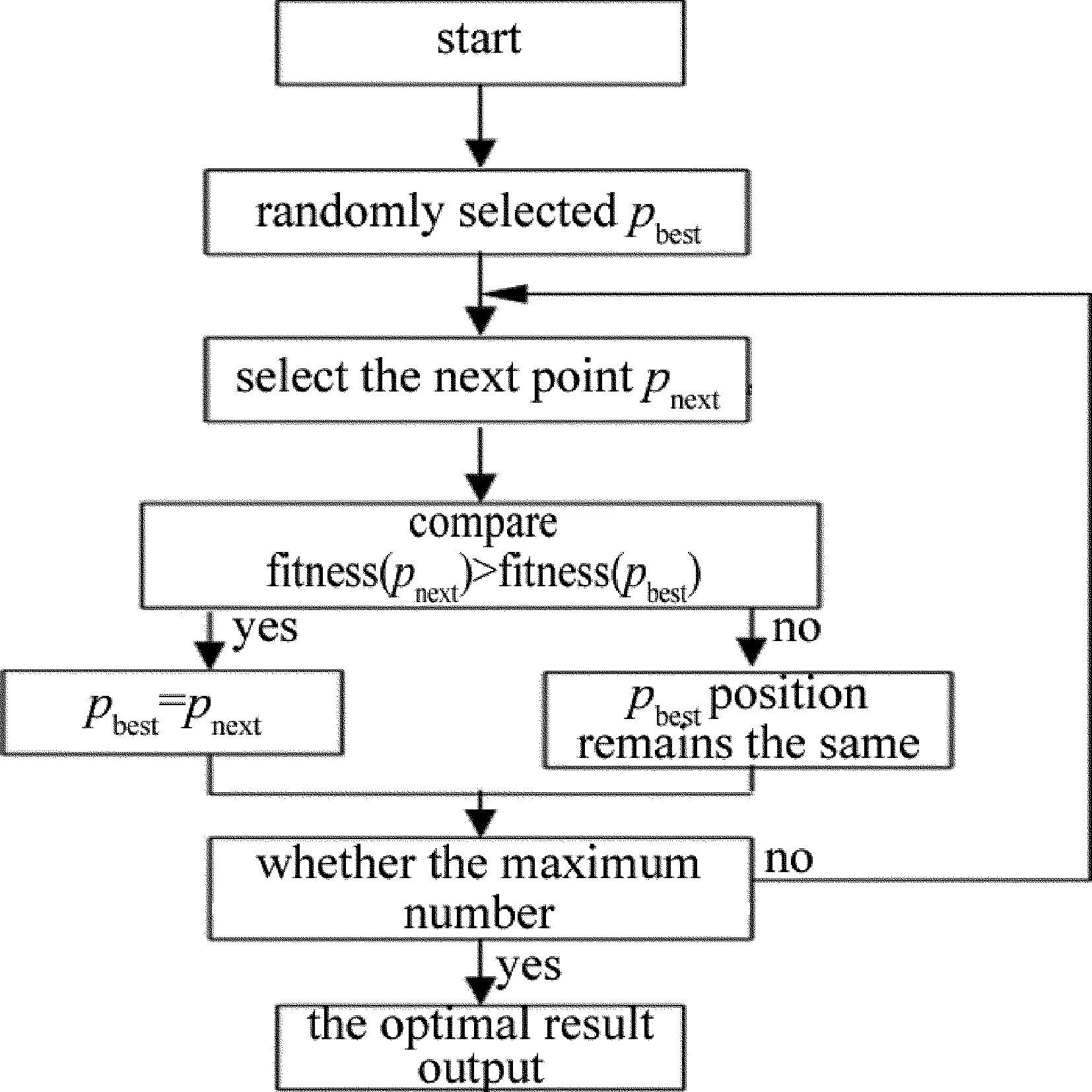
3.2 粒子群算法对参量的选择


5.1 实验数据

5.2 参量选择实验


5.3 加权组合核RX算法异常检测实验