有限可解群不可约特征标的非零元素

何立国, 张晓盼

(沈阳工业大学 理学院数学系， 辽宁 沈阳 110870)

有限可解群不可约特征标的非零元素

何立国, 张晓盼

(沈阳工业大学 理学院数学系， 辽宁 沈阳 110870)

对于有限可解群G,元素g∈G被称作是G的一个非零元，如果对于G的任一不可约特征标χ均有χ(g)≠0.有公开问题断言:可解群G的非零元素均在G的极大幂零正规子群(Fitting子群)里.我们利用群作用理论及正则轨道的方法证明了:如果可解群G的 Sylow 2-子群没有因子群同构于圈积Z2wrZ2，那么此猜想对G成立.

可解群； Fitting子群； 特征标

本文中利用Isaacs I M的书[4]作为标准符号和特征标论结果的主要出处.

在本文中,证明了下述结果:

定理A 如果可解群G的一个Sylow 2-子群没有因子群同构于圈积Z2wrZ2,那么不等式V(G)≤F(G)成立.

1 预备结果

下面引理列出V(G)的一些基本性质.

引理1[3]假定G是一个有限可解群，V(G)是其强非零子群.那么

(1)V(G)是G的一个特征子群.

(2) 若G是非交换群，则V(G)是G的一个真子群.

(3) 若N是G的一个正规子群,则V(G/N)在G中的原象包含V(G).

自动包药机串联自动核对机调剂模式在我院中心药房的建立与应用 ……………………………………… 顾 君等（15）：2135

引理2 假定V是一个特征为q的完全可约忠实p-模,此处P是一个p-群且(p,q)=1.如果P没有因子群同构于圈积ZpwrZp,则P在V里有一个正则轨道.

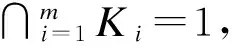
引理3[3]设M≤N是G的正规子群,如果θM=eη,θ∈Irr(N)，η∈Irr(M)及e是一个正整数,那么存在χ∈Irr(G)满足χ(a)=0对所有的a∈M-N.

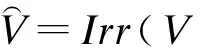
2 主要结论

定理A 如果可解群G的一个Sylow 2-子群没有因子群同构于圈积Z2wrZ2,那么不等式V(G)≤F(G)成立.

证明: 假定G是此猜想的极小反例.对于G的一个正规子群K,如果K/Φ(G)或K/Z(G)是幂零的,则K也是幂零的.因此,可以假定Φ(G)=Z(G)=1.设M1,M2,…,Mn是G的非平凡正规子群,且Ki=Core(Mi),它是Mi在G中的所有共轭的交.

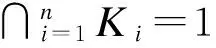
V((G/N)×(G/Kn))≤

V(G/N)×V(G/Kn),

V(G/N)≤F(G/N)，

V(G/Kn)≤F(G/Kn),

可得V((G/N)×(G/Kn))是幂零的，故其在G中的原象亦幂零.又V(G)嵌在V((G/N)×(G/Kn))在G的原象中,有V(G)≤F(G),矛盾.因此n=1,且G以共轭的方式忠实传递地作用在H1的共轭类集上.注意到H1是G的极大子群,得到G是一个本原可解置换群.由文献[7]可得G是F(G)与H的半直积,即G=F(G):H,Fitting子群F(G)是G的唯一极小正规子群,它是一个初等交换p-群.

因为G是极小反例，得N=V(V(G))是幂零的.又因为Φ(N)=Φ(G)=1,得N是唯一极小正规子群.显然N是一个初等交换p-群.可得V(G/N)是幂零的，故V(G)/N是幂零的.因此,记V(G)=P:Q，此处P≤N是一个正规Sylowp-子群且Q是V(G)的一个幂零Hall子群.Q在P上的共轭作用是忠实的,否则核K是非平凡的,且K∩Z(Q)≠1(因Q幂零).这意味着Z(V(G))是非平凡的,然而这与G的极小正规子群唯一性矛盾.

由于Φ(P)≤Φ(G)=1,可得P是初等交换群.进一步可得N≤P≤F(G)=N,故N=P,这是因为F(G)是G的唯一极小正规子群.

由文献[1]可知：所有G的非零元模F(G)的象是2-幂阶的,这些非零元模F(G)都在V(G/F(G))的Sylow 2-子群QF(G)/F(G)中， 可得幂零群Q是由2-幂阶元生成的，故它是2-群.得V(G)=F(G):Q,且Q是一个2-群.易见V(G)≤F2(G).此处F(G)是一个初等交换p-群.

若p=2,则V(G)也是一个2-群，因而是个幂零群,这是一个矛盾，因为G是一个反例.

[1] Isaacs I M,Navarro G,Wolf T R.Finite Group Elements where no Irreducible Character Vanishes[J].J.Algebra,1999,222:413-423.

[2] Moreto A,Wolf T R,Orbit Sizes.Character Degrees and Sylow Subgroups[J].Adv.Math.,2004,184:18-36.

[3] HE L G.Notes on Non-vanishing Elements of Finite Solvable Groups[J].Bull.Malays.Math.Sci.Soc.，2012，35(1):163-169.

[4] Isaacs I M.Character Theory of Finite Groups[M].New York:Academic Press,1976:198-216.

[5] Manz O,Wolf T R.Representations of Solvable Groups[M].Cambridge:Cambridge Univ.Press,1993:80-81.

[6] Zhang J P.A Note on Character Degrees of Finite Groups[J].Comm.in Algebra,2000,28(9):4249-4258.

[7] Huppert B.Endliche Gruppen I[M].Berlin-Heidelberg-New York:Springer-verlag,1967:182-183.

Non-vanishing Elements of Irreducible Characters of Solvable Groups

HE Li-guo， ZHANG Xiao-pan

(Shenyang University of Technology, Shenyang 110870, China)

LetGbe a finite solvable group.The elementg∈Gis said to be a non-vanishing element ofGifχ(g)≠0 for any irreducible characterχofG.It is conjectured that all of non-vanishing elements ofGlie in its Fitting subgroupF(G).Applying group action theory and regular orbit method,we prove that this conjecture is true for the solvable groupGwhich isZ2wrZ2-free.

solvable group; Fitting subgroup; character

2014-05-29

何立国(1967-)，男(回族)，黑龙江齐齐哈尔人，教授，博士，主要从事有限群及其特征标理论的研究.

2095-2198(2015)01-0088-03

10.3969/j.issn.2095-2198.2015.01.018

O152.1

A