基于二次函数拟合的太阳影子定位技术研究

马玉雪，令狐林玉，杨东海，孙国伟，买阿丽

(运城学院 应用数学系，山西 运城 044000)

基于二次函数拟合的太阳影子定位技术研究

马玉雪，令狐林玉，杨东海，孙国伟，买阿丽

(运城学院 应用数学系，山西 运城 044000)

利用影子长度和太阳高度角的关系研究太阳影子定位技术，得到太阳高度角为45度时影子和物体一样长；并通过对太阳影子长度变化的数据进行分析，得出影子长度与时间的二次函数拟合方程，从而根据影长最短的时间点确定拍摄地点的经度；然后根据太阳方位角与时角，经纬度，高度角之间的关系，求出高度角，从而得到影子和纬度的关系；最终确定出视频的拍摄地点和拍摄日期。

太阳高度角；太阳方位角；二次函数拟合；影子定位

0. 引言

太阳影子定位技术就是通过分析视频中物体的太阳影子变化，通过测量影子方位及长度与杆的实际长度、经纬度、时间等参数，确定视频的拍摄地点和拍摄日期的一种方法。

而物体影子的变化主要源于地球自转和绕太阳的公转，直杆位置及长度的测量是利用CCD相机线性成像的交比不变性原理和灭点产生原理，所以通过分析影响影子变化的参数，就可确定视频拍摄的地点和日期。

对于太阳影子定位技术考虑以下问题：

第一，建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律。

第二，当日期已知，直杆高度未知时，根据水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点。

第三，当日期与直杆高度都未知时，根据水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点和日期。

第四，根据一根2米高的直杆在太阳下的影子变化的视频，建立确定视频拍摄地点的数学模型，同时给出可能的拍摄地点。当拍摄日期未知，根据数学模型确定可能的拍摄地点与日期。

1. 直杆影子长度变化曲线

1.1 问题分析

影响影子长度的主要因素是杆子高度和高度角。首先确立影响太阳高度角[1]变化的因素并确定高度角的计算公式，然后利用影子长度和太阳高度角的三角函数关系，得到影子长度变化规律。以天安门广场北纬39度54分26秒,东经116度23分29秒位置(文中记为P点)，3米直杆在2015年10月22日北京时间9∶00-15∶00之间的太阳影子长度的变化曲线为例，说明这些量之间的变换关系。

1.2 确定影子长度与太阳高度角的关系

首先，我们确定太阳高度角[2]θ，收集资料可知太阳高度角θ的变化与太阳赤纬[3]δ、纬度φ和太阳时角[4]w三个因素有关：

(1)太阳赤纬δ与日期T有关，其关系式如下：

sinδ=0.39795cos[0.98563(T-173)]

(1)

其中T=1表示1月1日，T=365表示12月31日。

(2)纬度，其数值在0至90度之间。

(3)太阳时角w是指日面中心的时角，可以由北京时间得到，设北京时间为t,以24小时计，经度为φ，可以得到关系式[3]：

w=15°×[t+(120°-φ)÷15°-12]

(2)

根据图1，确定出了这三个因素关系式为[2]：

sinθ=sinφsinδ+cosφcosδcosw

(3)

最后建立函数模型，确立影子长度与太阳高度角θ的函数关系，如图2所示，设直杆高度为h米，影子长度为l米，可以得到函数模型为：

(4)

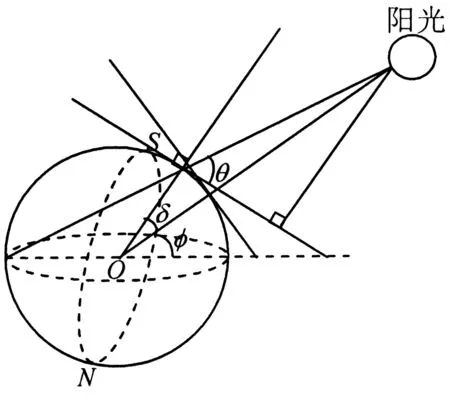
图1 太阳高度角计算示意图

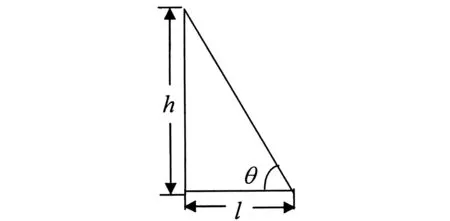
图2 影子长度与太阳高度角的关系图

1.3 画出变化曲线图

应用建立的模型，确立了P点3米高的直杆在2015年10月22日北京时间9:00-15:00之间的太阳影子长度随时间变化的二次函数关系，其中由计算可得φ=116.39,φ=39.9072,h=3,T=265，从而用Matlab画出了北京时间9:00-15:00之间该地的太阳影子长度的变化曲线，如图3所示。

分析可知，如果为东经120度时，北京时间12点时影子长度最短，又因为每晚4分钟，经度偏西1度，而天安门广场经度为东经116度23分29秒，比东经120度少3.61度，所以该地的时间要比标准北京时间要晚14.44分钟，所以天安门广场影子最短的时间为12点14分26秒。

一天中影子变化的规律是早晚影子最长，中午最短，早上到中午影子慢慢变短，中午到晚上影子慢慢变长。从上面二次函数模型中可以得到：影子与太阳高度角的关系是，太阳高度角越小，影子越长。太阳高度角为45度时影子和物体一样长。

2. 日期已知，直杆未知求地点

2.1 问题分析

已知日期时，获得的某地杆子不同时间的顶点坐标，确定拍摄地点所在的经度和纬度，方法具体如下：

第一步，由已知数据得出影子长度，然后对这些数据进行二次函数拟合，得出影子长度与时间的关系，从而根据影子最短距离的时间点确定可能点的经度；

第二步，由获得的经度，根据太阳方位角[4]与时角，经纬度，高度角之间的关系，求出高度角，然后根据影子和纬度的关系确定出可能的纬度，从而确定拍摄地点所在的经度和纬度。

2.2 给定日期和固定直杆确定位置

2.2.1 确定经度

对于该种情况，我们收集了2015年4月18日的一段时间的影子长度数据，得出影子长度与时间的关系如下表1所示。

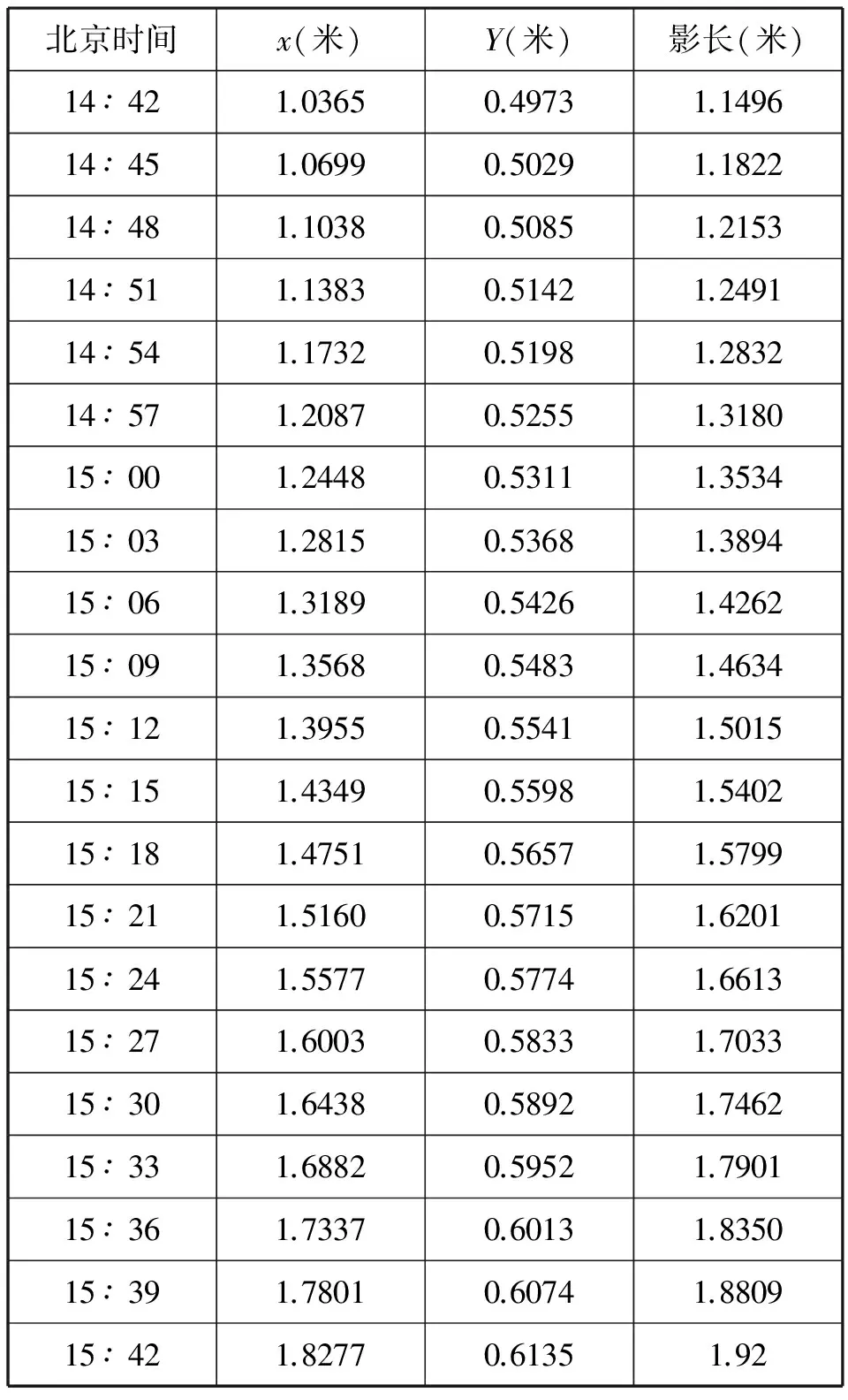
表1 2015年4月18日某地影子长度与时间的关系

建立二次函数模型，利用Matlab对影子长度和时间t的数据进行拟合分析，得到系数a=0.1473,b=3.7519,c=24.1325的抛物线，从而确定出影子长度与时间的关系为(如图4)：

l=0.1473t2-3.7519t+24.1325

(5)

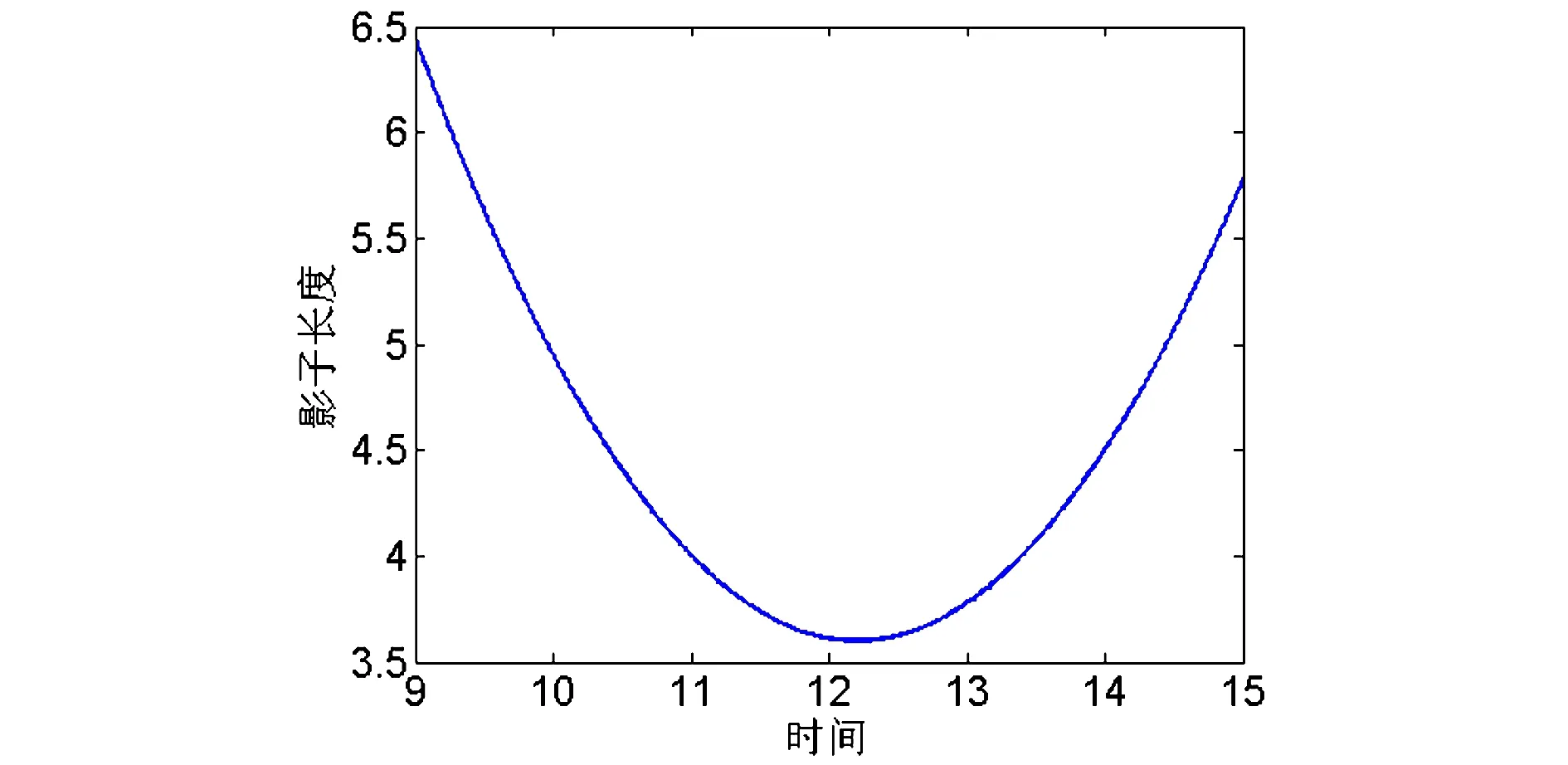
图3 3米高直杆的太阳影子长度与时间的关系

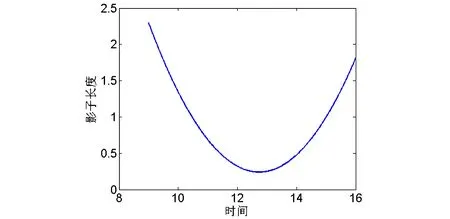
图4 表1的影子长度与时间的关系

由方程(5)可知，该地的影子最短的时间为抛物线最低点12.736，所以时间为12点44分9秒。比东经120度的影子最短的时间晚44.16分钟，又因为每晚4分钟，经度偏西1度，所以该地比东经120度偏西11.04度，为东经108.96度。

2.2.2 确定纬度

首先，由文献[5]获得的太阳方位角α与高度角θ、太阳赤纬δ、太阳时角w之间的关系确定出太阳方位角α的计算公式[4]：

(6)

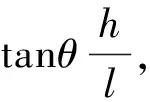
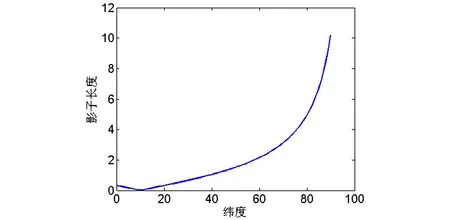
图5 4月18日的正午时刻影长与纬度的关系

由抛物线得到正午时刻的最短影长为0.241米，然后由纬度和影长的关系可以得出该地纬度为18.3度，由于2015年4月18日太阳直射点在北纬10度，又因表1的数据为下午的影子轨迹，可以得到直杆是在太阳直射点以北，所以应该为北纬18.3度。

由以上分析可得到直杆所处的可能地点为东经108.96度，北纬18.3度。

3. 日期与杆长都未知求地点

3.1 问题分析

对数据进行二次函数拟合，根据影子最短距离的时间点比较分析确定两组数据直杆所在地的经度；对于日期不确定，遍历一年365天，确定每一个T之后，得出日期，然后可得到正午时刻同一经度下，纬度与影长的关系，从而确定纬度。

3.2 建立二次函数模型

利用Matlab对文献[6]附件2和附件3中的两组数据进行分析处理，得出影子长度与时间关系的二次函数方程分别为：

l1=0.0981t2-2.8809t+21.731

l2=0.2964t2-7.5007t+47.5619

如图6，图7所示。

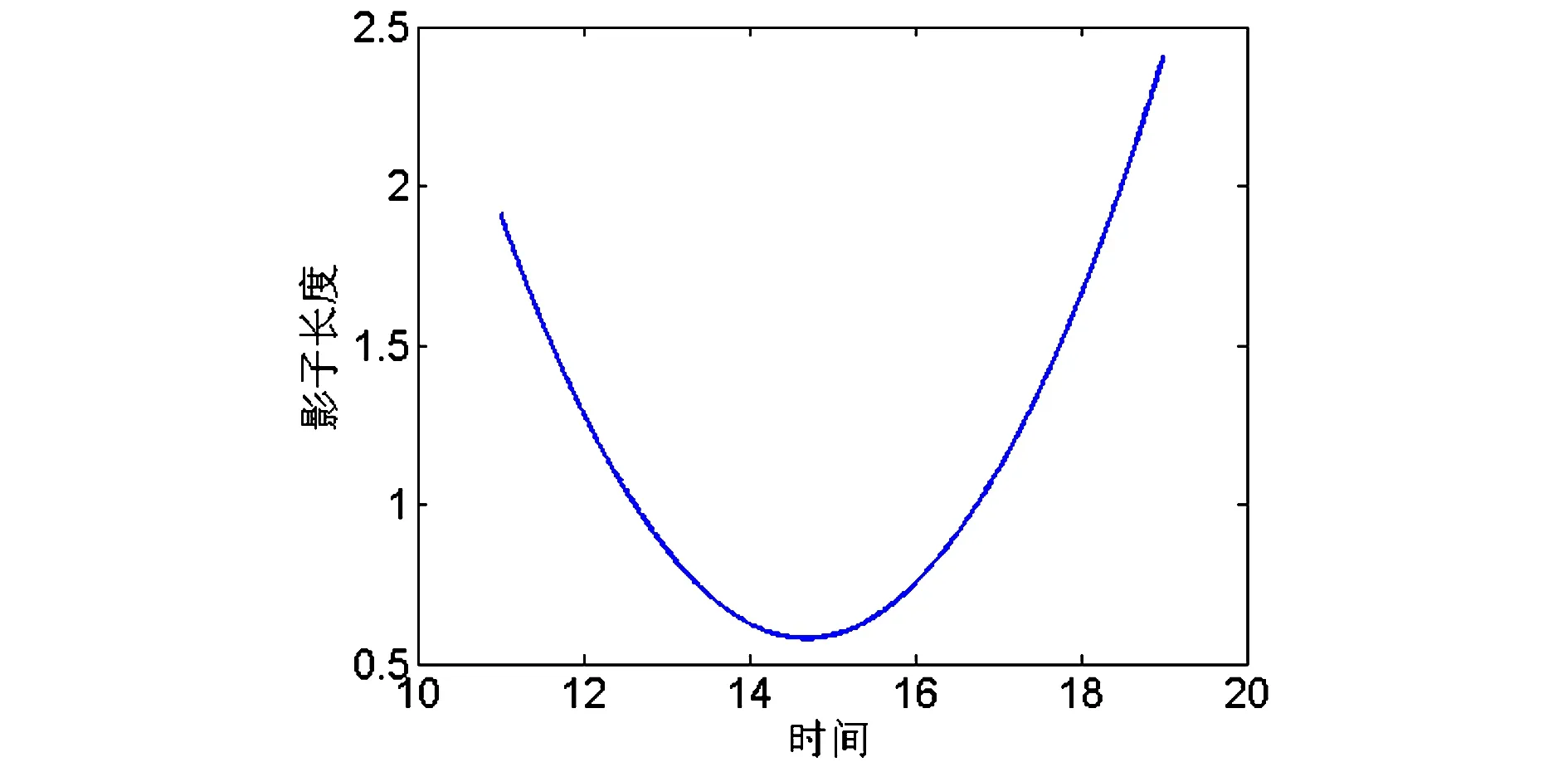
图6 第一组影子长度与时间的关系

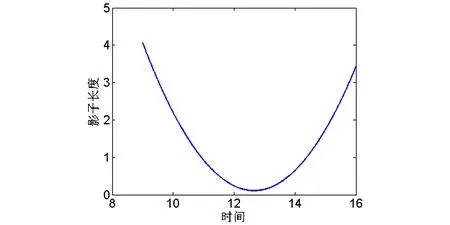
图7 第二组影子长度与时间的关系

当日期未知时，遍历一年365天，即T∈[1,365]且T∈Z*,确定每一个T之后，用反演法确定出日期，第一组数据日期为7月20日，第二组数据日期为1月20日，可得积日T1=201,T2=20，然后可得到正午时刻同一经度下，影长与纬度的关系分别为图8，图9所示。

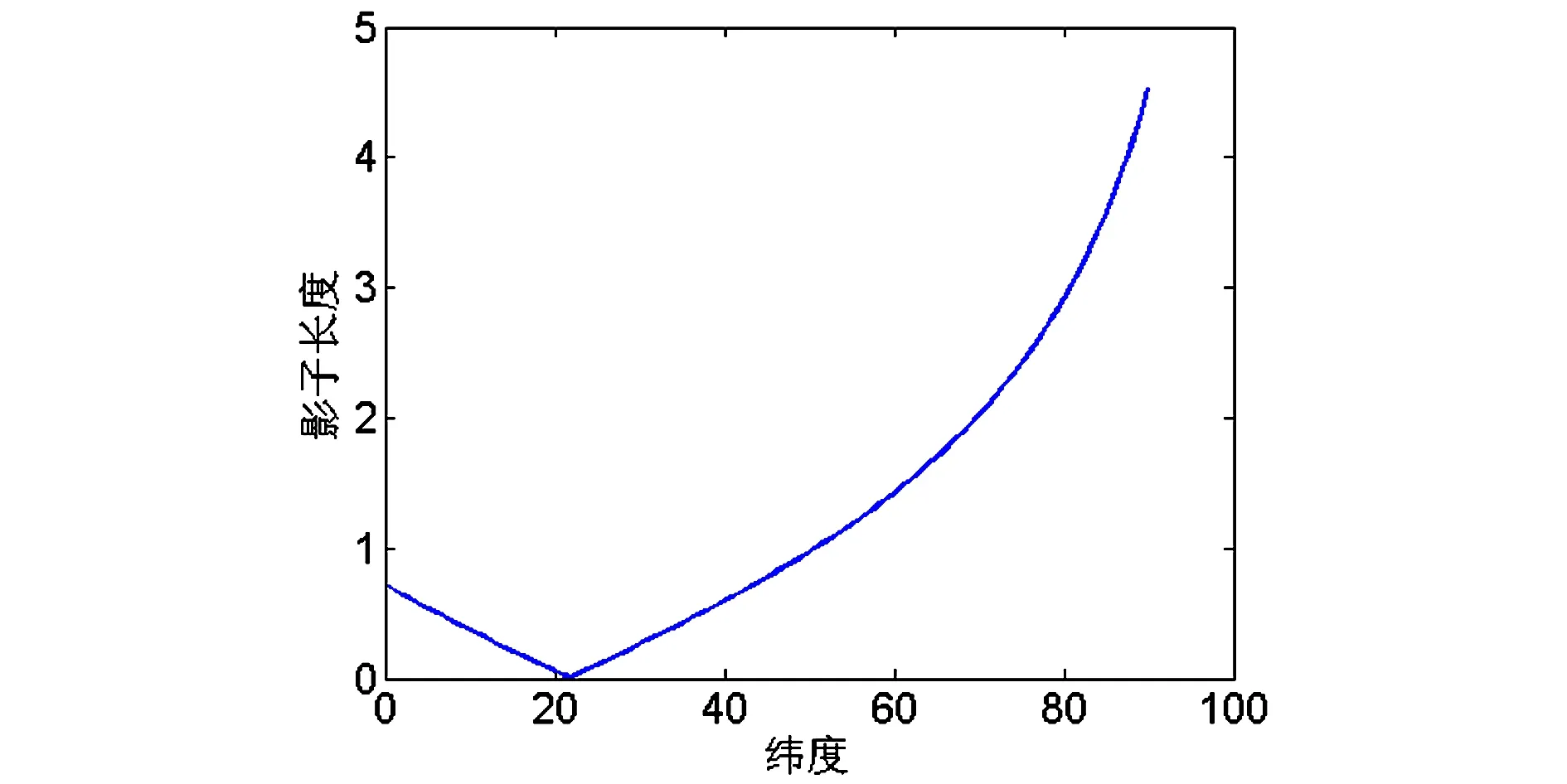
图8 7月20日正午时刻影长与纬度的关系

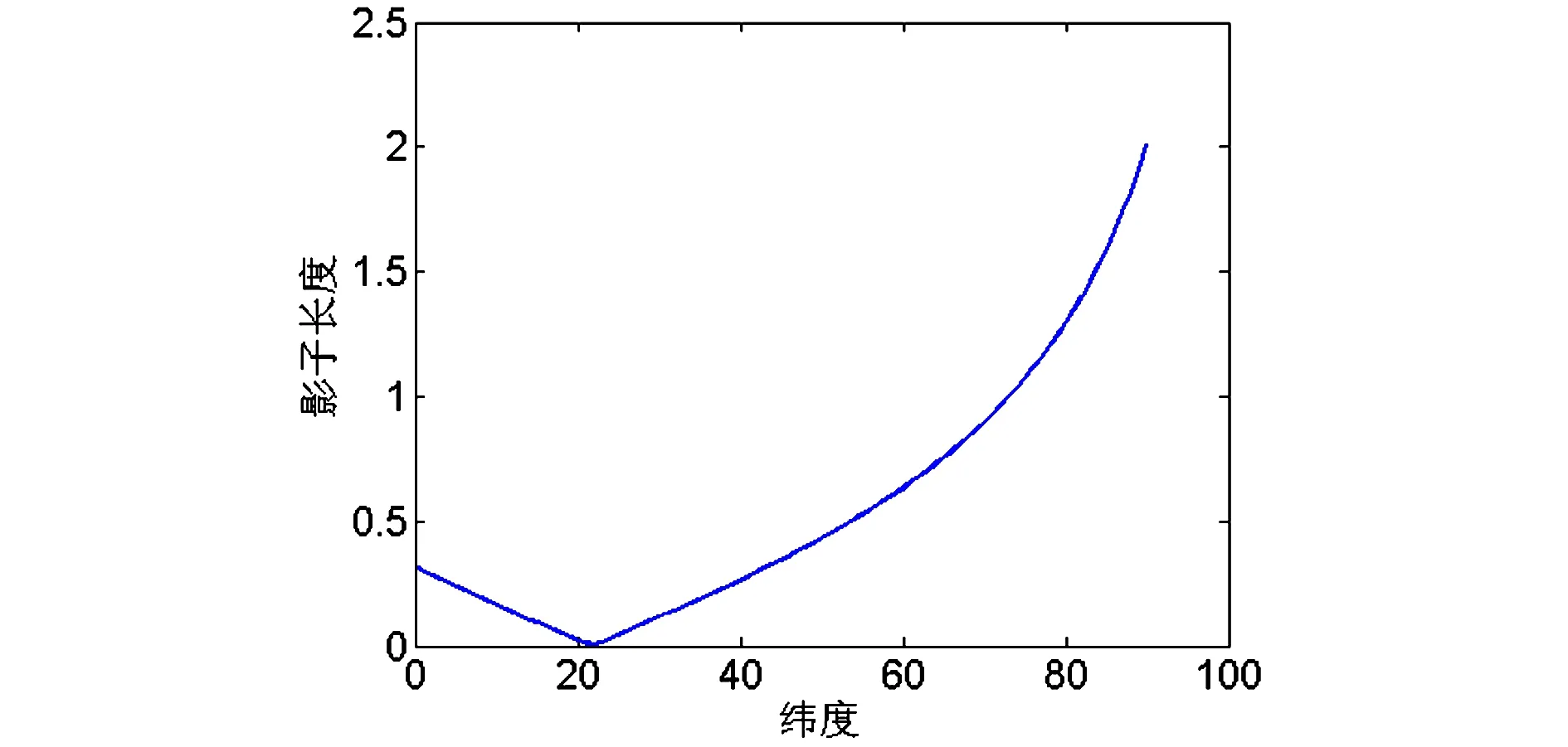
图9 1月20日正午时刻影长与纬度的关系

所以可得该地点为东径79.75度，北纬39.22度，日期为7月20日，另一个地点为东径10.25度，北纬29.39度，日期为1月20日。

4. 日期未知，杆长已知求地点

4.1 问题分析

先将视频导入Matlab，然后每2分钟取一帧，得到21张有序的图片，然后对每张图片进行灰度处理，得到每张图片中影子顶点在矩阵中的位置，即像素点的坐标，然后通过像素点坐标及像素点间的距离和实际长度的比较，得到影子轨迹的实际坐标，计算出经、纬度，得出可能的拍摄地点。然后在日期未知的情况下，利用二次函数拟合模型求得可能的拍摄地点和日期。

5.2 根据杆长与时间求地点

4.2.1 确定经度

先将视频导入Matlab，并结合小孔成像原理，得到影子顶点轨迹的实际坐标和实际影子长度与时间的关系如下表2所示。利用Matlab分析影子长度l和时间t的数据进行二次函数拟合，得到系数：

a=0.0877,b=-2.4423,c=17.1244

从而得出影子长度与时间的关系抛物线方程为：

l=0.0877t2-2.4423t+17.1244

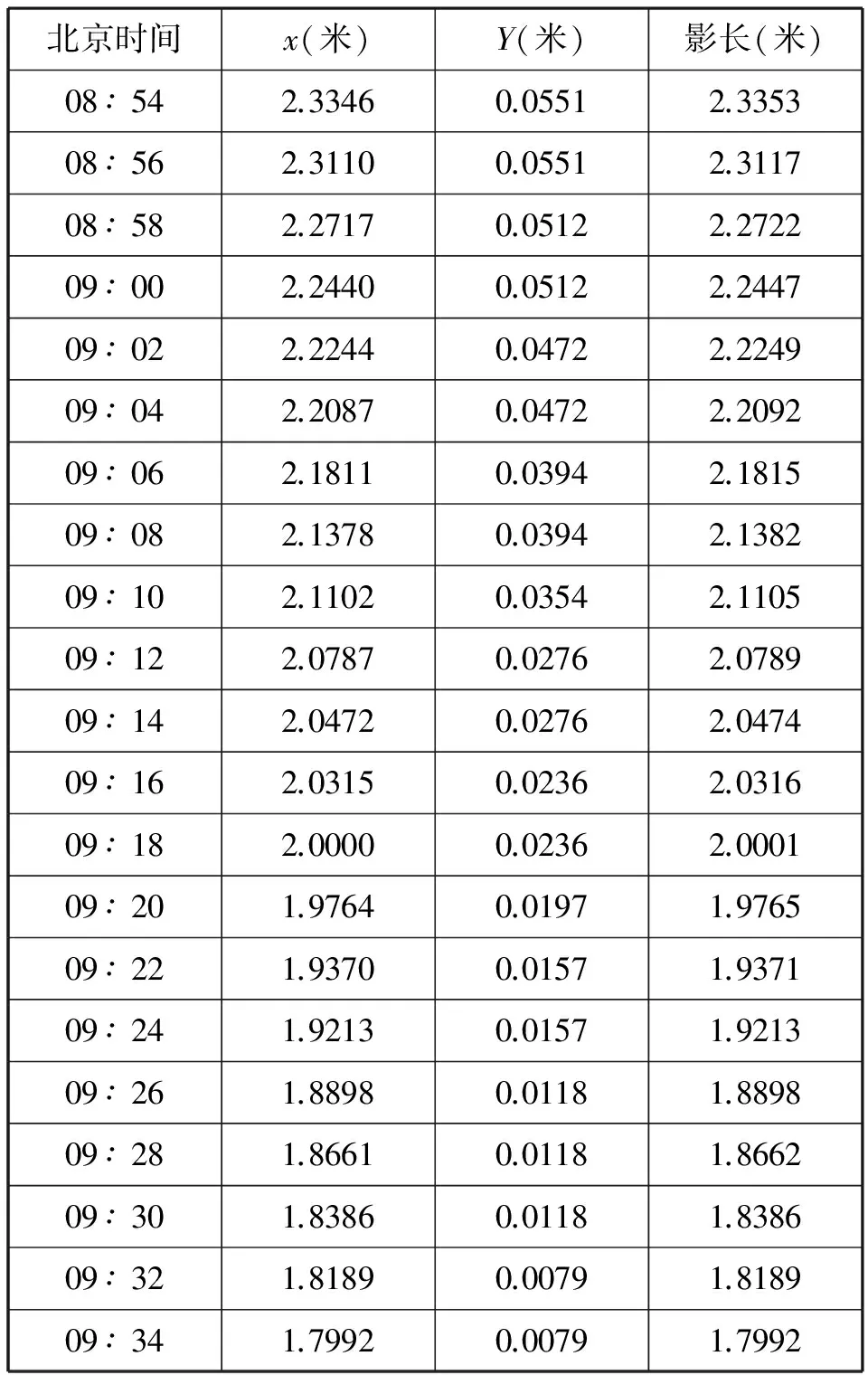
表2 2015年7月13日某地影子长度与时间的关系

用Matlab对数据做出影子长度与时间的关系符合抛物线，如图10所示。

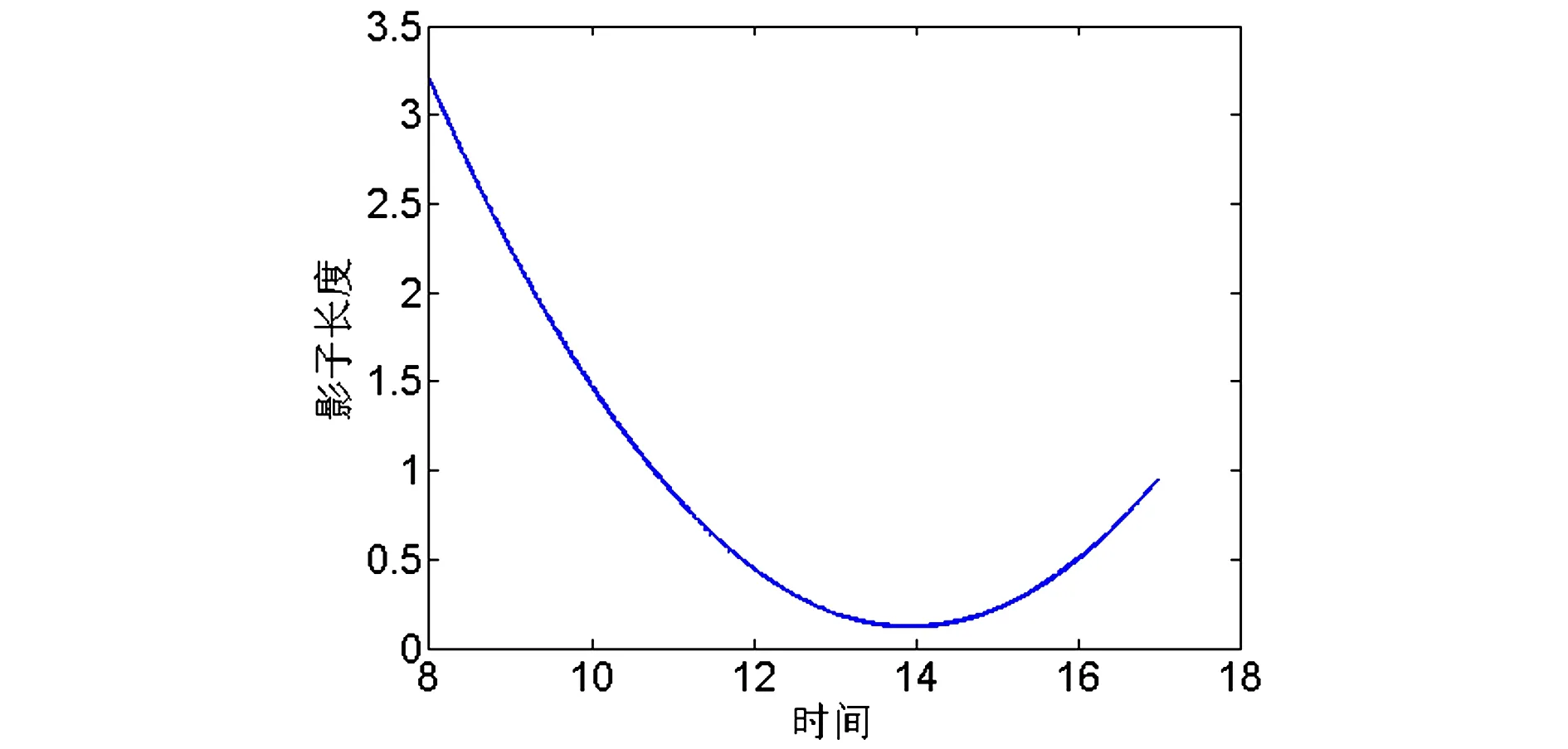
图10 表2的影子长度与时间的关系

由方程可知，该地的影子最短的时间为抛物线最低点，时间为13点55分27秒。比东经120度的影子最短的时间晚1小时55分27秒，又因为每晚4分钟，经度偏西1度，所以该地比东经120度偏西28度52分，为东经91.13度。

4.2.2 确定纬度

由上述二次函数确定出了最低点为13.9242，0.1209，可以得到在时间为13点55分27秒，经度为东经91度8分时，影子最短为0.1209米，而由题可知杆长h=2米，日期为2015年7月13日，可得积日T=194，然后由第一问影子长度与太阳高度角的关系，可得到正午时刻同一经度下，纬度与影长的关系，如图11所示。

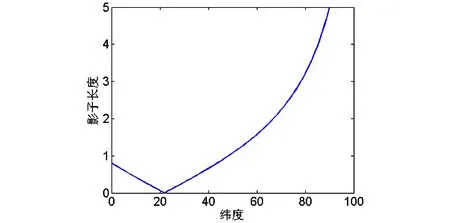
图11 表2的影长与纬度的关系

由抛物线得到正午时刻的最短影长为0.1209米，然后由纬度和影长的关系可以得出纬度为北纬26度和北纬20度，由于2015年7月13日太阳直射点在北纬23度，由于视频中的影子往北面移动，可以得到直杆是在太阳直射点以北，所以应该为北纬26度。

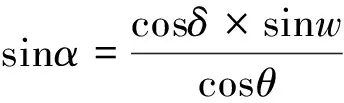
由模型可以得出该地点的经度为东经91.13度，北纬26度。

5.结束语

本文利用二次函数拟合方法研究太阳影子的定位技术，给出了确定视频拍摄的地点和日期的一种方法。当视频中没有直杆时，如何确定拍摄地点和拍摄日期是后续需要研究的一个方向。

[1] 屈名,王征兵,王德麾.基于交比不变性的太阳定位算法的研究[J].硅谷,2013(19).

[2] 费云霞,王春顺.对太阳高度角的了解及其计算方法[J].中小企业管理与科技,2008(1).

[3] 罗新宇.太阳赤纬的近似计算[J].铁路航测,1993(2).

[4] 百度百科，太阳时角[EB/OL].[2015年9月12日]http://baike.baidu.com/link?url=h1Munt6Ctv0KtBIaY7-6HTmTf2w1uDOSQJ0bxzbBQnklF2ElnEQAQ8vC_0Z7raZVAUDhm5UyhPXHBdzhehmI-_

[5] 贺晓雷,于贺军,李建英,等.太阳方位角的公式求解及其应用[J].太阳能学报,2008(1).

[6] 全国大学生数学建模网, 2015年高教社杯全国大学生数学建模竞赛赛题[EB/OL].2015年9月12日，http://www.mcm.edu.cn/html_cn/block/c61dfec317d7a5bd9b2b8efed81c8af3.html

【责任编辑 荆 瑶】

Solar Shadow Positioning Technology Based on Quadratic Function Fitting

MA Yu-xue, LINGHU Lin-yu, YANG Dong-hai, SUN Guo-wei, MAI A-li

(DepartmentofAppliedMathematics,YunchengUniversity,Yuncheng044000,China)

In this paper, solar shadow positioning technology was studied. Using the relationship between shadow length and sun elevation angle, the shadow length was obtained as long as the object when solar elevation angle is 45 degrees. By analysising the solar shadow length varying data by fitting equation, a quadratic function of the length of the shadow was obtained. According to the shortest time, this is shadow shortest time, to determine longitude. Then according to the relationship between the sun angle and azimuth, longitude latitude, elevation angle, the elevation angle is calculated, and the relationship between shadow and latitude are determined. Finally, filming locations and recording date of the video were determined.

Solar elevation angle; Solar azimuth; Quadratic function fitting; Solar shadow positioning technology

2015-08-16

山西省高等学校科技项目(20121113)；运城学院科研基金项目(XK-2014030,XK-2014035)

马玉雪(1994-)，女，山西潞城人，运城学院应用数学系1301班学生。

TP391.7

A

1008-8008(2015)06-0024-05